基于异同性的社区演化分类方法
2021-07-29刘业强王鲁杨圣彬刘亚琼
刘业强,王鲁,杨圣彬,刘亚琼
基于异同性的社区演化分类方法
刘业强1,王鲁1,杨圣彬2*,刘亚琼2
1. 山东农业大学信息科学与工程学院, 山东 泰安 271018 2. 山东农业大学网络信息技术中心, 山东 泰安 271018
动态网络中的社区演化分析是目前的研究热点之一,其在舆论控制、网络营销和个性化推荐服务等方面有着重要作用。提出一种基于节点重要性评价指标的差值吸收核心节点检测算法,首先计算各节点的相对权重值,进而划分核心节点,并以此为基础优化差异性公式,提出一种异同性社区演化分类模型,从相似性和差异性两方面对演化类型进行划分。将提出的分类模型与GED及SGCI在HEP-TH和波兰政治博客圈数据集上进行比较,实验结果表明,提出的分类模型在整体上优于GED及SGCI,尤其在Forming和Dissolving事件的检测时,可以做到对小社区敏感,能检测到小社区的多种演化类型。
聚类系数; 核心节点检测; 社区演化分类模型
社交网络被定义为以图形表示的信息网络,可以描述个体之间的交互行为。在社交网络中,个体由网络中的一个节点来表示,边则表示个体之间的交互作用或者个体间存在的某种关系。例如,在因特网中人与人之间的联系,即思想、信息的交换可以被建模为一个社交网络;科学家合作网中,节点表示作者,两作者合作产生文章即表示一条边。社区结构是社交网络的特性,即同一社区内的节点联系较为紧密,社区间的节点联系较为松散。同一社区内的成员通常有着某一共性,例如兴趣爱好、研究领域和文化交流等。当有新节点加入网络,现有节点离开网络,现有节点与其他节点建立新联系或现有节点与其他节点的联系消失时,社交网络会产生演化行为,变化的网络即为动态社交网络[1]。动态社交网络社区演化分析以动态社区发现的结果为基础分析社区变化,如生长、分裂、收缩和消失等。社区演化分析可以发现网络潜在的演化规律,推导个体之间的交互模式,在定向营销和广告、舆论控制、蛋白质网络、传染病控制等方面有着广泛的应用[2]。
对社区演化的分析通常分为两方面,一是判断不同时序的社区是否具有演化关系,常用的方法是基于相似度的演化分析和基于核心节点的演化分析;二是判定演化类型,需要建立社区演化分类模型来判定[3]。基于相似度的演化分析算法以相邻两个时间片内社区之间的相似性为标准来判断社区的演化事件,社区相似性多以Jaccard系数为度量,但此方法忽略了网络的拓扑结构信息,同时阈值的选择也有很大的不确定性;基于核心节点的演化分析利用具有稳定性的核心节点来代表整个社区,分析社区的演化行为。Bhat等[4]提出基于密度的核心节点演变分析方法,根据节点在一定邻域范围内的密度来选择网络中的核心节点,并且在每个时间片更新增量节点的属性;Yin等[5]提出基于引力关系重构的核心节点演化分析算法,将引力的概念引入社交网络进行社区发现;Dhouioui等[6]提出了一个识别演化事件的框架,该框架要求在每个社区范围内都找出核心节点,并且将边缘度更小的节点加入核心节点集合,然后根据核心节点变化识别演化事件。社区演化分类模型可以用来判定演化类型。2012年,Bródka等[7]提出了演化模型GED,将社区演化分类为七种类型,包含了社区从生成到消失的整个生命周期,并首次增加了节点重要度的概念。同年,Gliwa等[8]提出了一种基于稳定聚类的演化分析方法SGCI,提出了与GED不同的演化分类模型,认为噪声聚类对演化结果没有实质影响。
本文提出的差值吸收核心节点检测算法基于节点重要性评价指标p[9],该指标由节点邻居信息以及集聚系数计算得出,只需考虑节点的邻居个数以及其邻居之间的连接紧密程度等局部信息,因此对大规模网络同样可以进行有效分析。该算法以p为基础,将有边连接的两节点进行一一比对,p值较大的节点其权重值增加,p值较小的节点其权重值减少。由此方法确定核心节点集,改进差异性公式,并结合现有的相似性公式,提出一种异同性社区演化分类模型(the classification model of community evolution based on similarities and differences, SDCE),从相似性和差异性两方面判定演化类型。
1 相关研究
1.1 节点重要性评价指标
节点重要性评价指标p综合考虑节点的邻居个数以及其邻居之间的连接紧密程度,只考虑网络局部信息,因此算法时间复杂度较低,其计算式为:
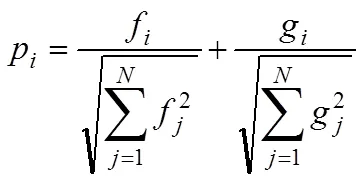
式中:f为节点自身度与其邻居度之和, 其计算式表示为:
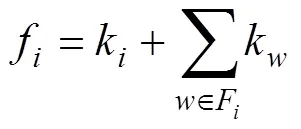
式中:k表示节点的度,F表示节点的邻居节点集合。g计算式表示为:
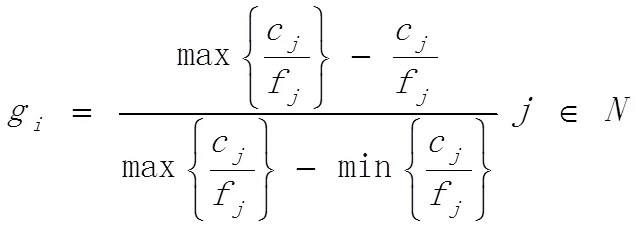
式中:c为节点的聚类系数,g是对c/f的归一化处理。
1.2 差异性公式
差异性公式由Zygmunt等[10]提出,算法共分两步,首先基于PageRank算法计算节点的重要性排名,之后以共有节点的变化幅度反映社区的变化幅度,其计算式为:
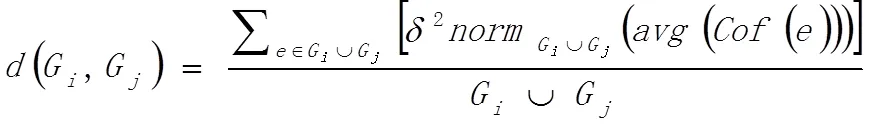
式中:=indexG()=indexG(),indexG()表示节点在G中的重要度排名;表示节点重要度,基于PageRank及历史社区信息计算得出。
1.3 相似性公式
相似性公式以Jaccard相似度公式为基础进行改进,通过节点对社区进行相似性判断[11],其计算式为:
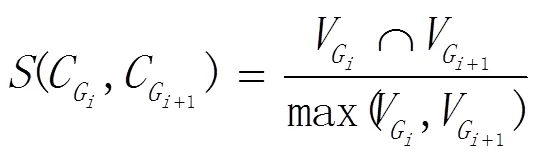
1.4 GED演化分类模型
GED以Jaccard相似度评估公式为基础,增加了节点重要度的概念,将其作为判定标准,对社区间的相似度进行判定,进而划分事件类型。演化类型分为七种,以改进的相似度公式I(G,G)对演化进行判定,其中:
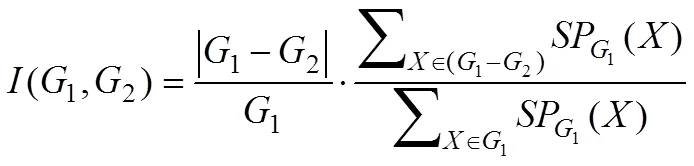
每种演化类型判别如下:
[1] Forming(生成):对于2:(12)<10% and(G,G)<10%,其中G∈T,G∈T1,此时社区G生成。
[2] Continuing(持续):(12)≥and(21)≥and12.
[3] Growing(生长):(12)≥and(21)≥and12OR(12)≥and(21)
[4] Shrinking(萎缩):(12)≥and(21)≥and12OR(12)<α and(21)≥and12,且2只能与前一时间窗口T中的一个社区匹配成功。
[5] Merging(合并):(12)≥α and(21)
[6] Splitting(分裂):(12)
[7] Dissolving(消失):对于1:(12)<10% and(21)<10%,其中1∈T,2∈T1,此时社区1消失。
2 算法描述
2.1 差值吸收核心节点检测算法
通常,一个节点的权重越高,它在社区中的影响力就越大,对社区相似性检验以及演化类型的判断起着重要作用。社区中核心节点的选择是关键部分,提出的差值吸收核心节点检测算法,以节点重要性评价指标p为基础,对有边连接的两个节点进行一一比较,依据比较结果得到相对权重值,确定核心节点。算法分为三步:第一步,计算每个节点的p值;第二步,初始化节点权重值CoC(N)为0,对有边连接的两节点进行一一比较,p值较大的节点,其CoC(N)值增加;p值较小的节点,其CoC(N)值减少。第三步,遍历节点,选取CoC(N)值大于0的节点即核心节点,放入核心节点集并返回。其中表示两节点p差值的绝对值。算法第一步只考虑节点及其邻居关系而非整个社区,第二步只需遍历边集,因此算法时间复杂度较低,对大社区同样可以进行有效分析。

算法1差值吸收核心节点检测算法 输入:节点集V,边集E 输出:核心节点集CoreNodeSet 1. for every node vi∈V do 2. calculate the pi by (1); 3. end for 4. CoC(Ni)=0, i∈[1, n]; 5. for edge e∈E do 6. DV=|pi - pj|; 7. Ni,Njare nodes connected with e; 8. if pi > pj then 9. CoC(Ni) = CoC(Ni) + DV; CoC(Nj) = CoC(Nj)-DV; 10. else if pi < pj then 11. CoC(Ni) = CoC(Ni)-DV; CoC(Nj) = CoC(Nj) + DV; 12. end if 13. end for 14. for every CoC(Ni) do 15. if CoC(Ni) > 0 then 16. Input code vi into CoreNodeSet; 17. end if 18. end for 19. return CoreNodeSet
文献[6]中给出了10个节点的网络图(图1),并计算出了各节点的p值。依据该核心节点检测算法可得各节点的CoC(N)值,如表1所示。由结果可知,节点2,3,4,6,8的CoC(N)值大于0,因此核心节点集为{2,3,4,6,8}。下文将以得到的核心节点集和CoC(N)值为基础,分别从节点的选择、节点的影响力值等方面改进差异性公式,对社区的差异性进行判断。
图1 10个节点的网络图
Fig.1 Network diagram of 10 nodes
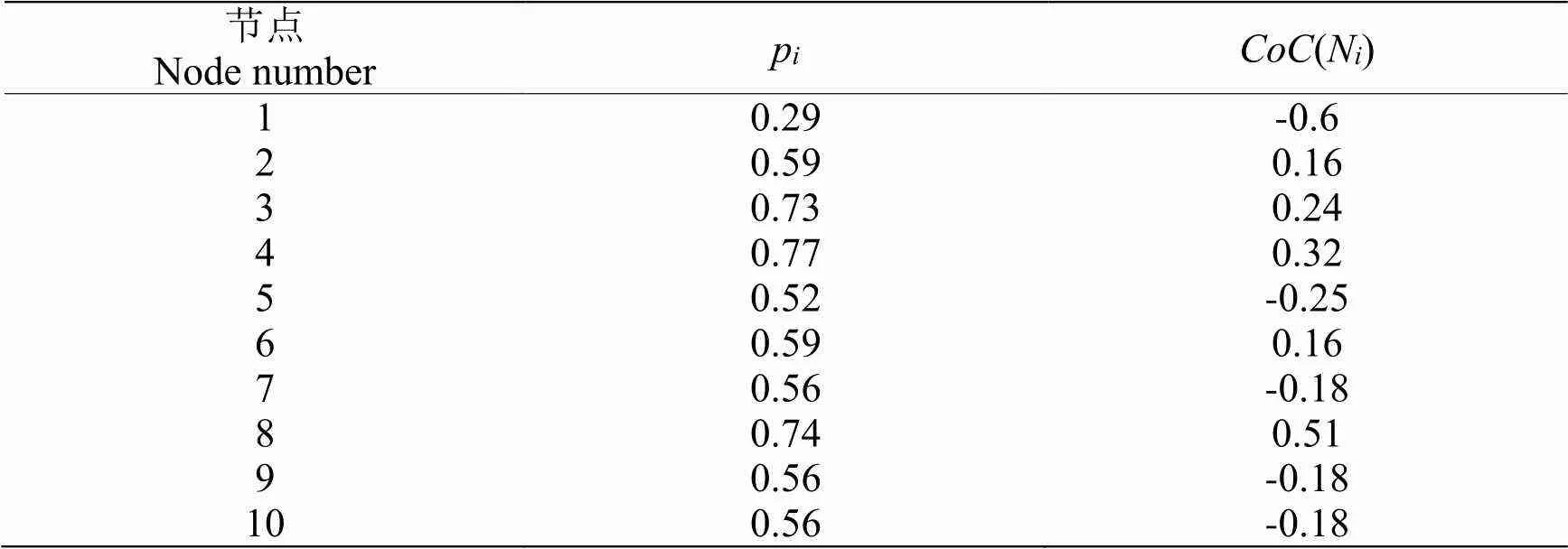
表1 各节点CoC(Ni)值
2.2 基于核心节点集的差异性公式
社区演化评估公式也称为社区相似度评估公式,通过比较两个社区的一些特征来评估两个社区是否足够相似。为了挖掘演化关系,需要将两个相邻时间窗的社区进行一一比对,判断其是否相似。区分于GED等,提出的异同性演化分类模型从相似性和差异性两方面进行判定,相似性以jaccard相似度为基础,从宏观层面体现了社区拓扑结构的共性;差异性以核心节点为基础,从微观层面体现了核心节点的变化对社区的影响。其中,相似性公式为式(5),差异性公式在式(4)的基础上进行优化,表示为:
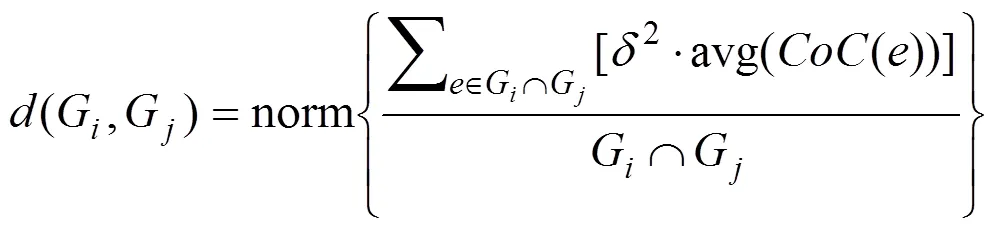
其中主要有三方面的改进,一是节点的选择,原文中代表所有节点,式(7)将其优化为核心节点集中的节点,以体现核心节点对社区演化的主导作用;二是将式(4)中的影响力值()替换为由评价指标p计算得出的节点权重值();三是在计算过程中发现,由于分母为G∪G,导致会出现核心节点只存在于G或只存在于G的情况,此时的计算是无意义的,因此改为G∩G,可有效降低算法时间复杂度。
2.3 异同性社区演化分类模型
提出的SDCE模型以现有的相似性公式和改进的差异性公式为判定依据,从社区间的相似性和差异性两方面对社区演化类型进行判定。按照GED分类模型对异同性分类模型进行分类,共分为Continuing, Shrinking, Growing, Splitting, Merging, Dissolving和Forming七种类型,分类标准如下:
[1] Forming(生成):对于前一时间窗口1的任一社区,社区与都不满足≤且≥;
[2] Continue(持续):在后一时间窗口1中只能找到一个社区与社区满足≤且≥且;
[3] Growing(生长):在后一时间窗口1中只能找到一个社区与社区满足≤且≥且;
[4] Shrinking(萎缩):在后一时间窗口t+1中只能找到一个社区与社区满足≤且≥且;
[5] Merging(合并):在前一时间窗口1中能找到大于等于2个社区,且任一社区与社区都满足≤且≥且;
[6] Splitting(分裂):在后一时间窗口1中能找到大于等于2个社区,且任一社区与社区都满足≤且≥且;
[7] Dissolving(消失):对于后一时间窗口1中的任一社区,社区与都不满足≤且≥;
本节首先提出差值吸收核心节点检测算法,得到社区核心节点集和各节点的相对权重值(N),以此为基础改进差异性公式,并将改进的差异性公式应用于演化类型的判定标准中,对演化类型进行分类。
3 结果分析
为了验证异同性演化分类模型SDCE的有效性,将此模型与GED及SGCI在测试数据集HEP-TH和波兰政治博客圈数据集上进行对比实验。其中HEP-TH来源于arXiv,波兰政治博客圈(Salon24)来源于www.salon24.pl网站。本文的实验环境为Matlab R2018b(V9.5)。
3.1 参数确定
异同性分类模型共有两个参数:、。对两参数分别赋值,分析实验结果以选择最优参数值。实验中部分较优结果如图2和图3所示。参数值的确定主要考虑两方面,一是各类型演化事件数,二是演化事件总数。我们期望得到最多的演化结果(图3),但由图2可知,当>0.3以后,Growing、Shrinking、Merging和Splitting数量以较快的速度减少,尤其是Growing、Merging和Splitting三类值急剧减少,最低值降为0,因此将值设置为0.3。同样,综合考虑演化事件总数及各类演化事件,将值设为0.2。以同样方式对波兰政治博客圈数据集进行分析,得出=0.3,=0.3时可得到最优结果集。
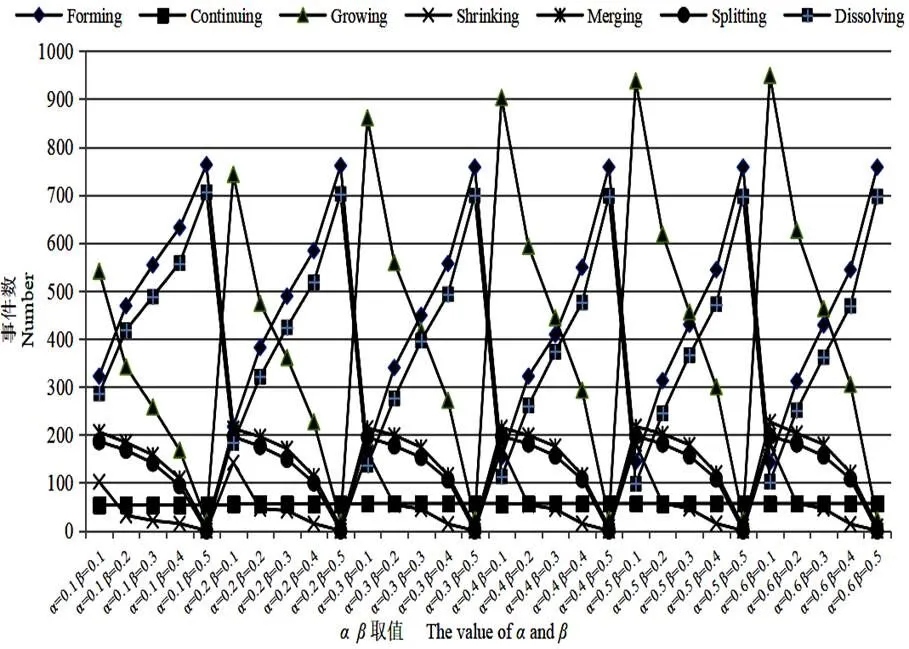
图2 不同参数下各类演化事件数
Table 2 Number of evolution events under different parameters
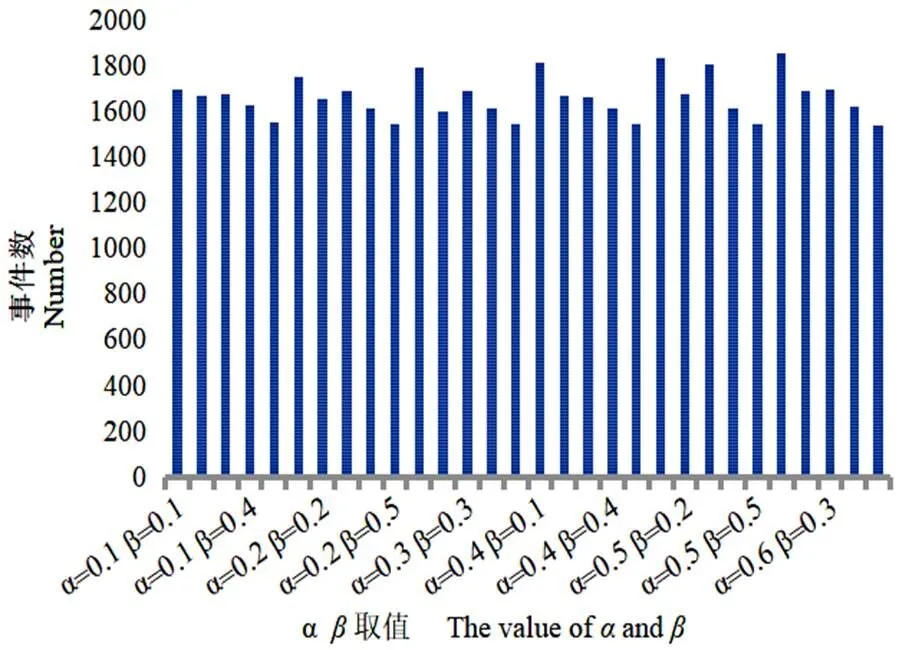
图3 不同参数下总演化事件数
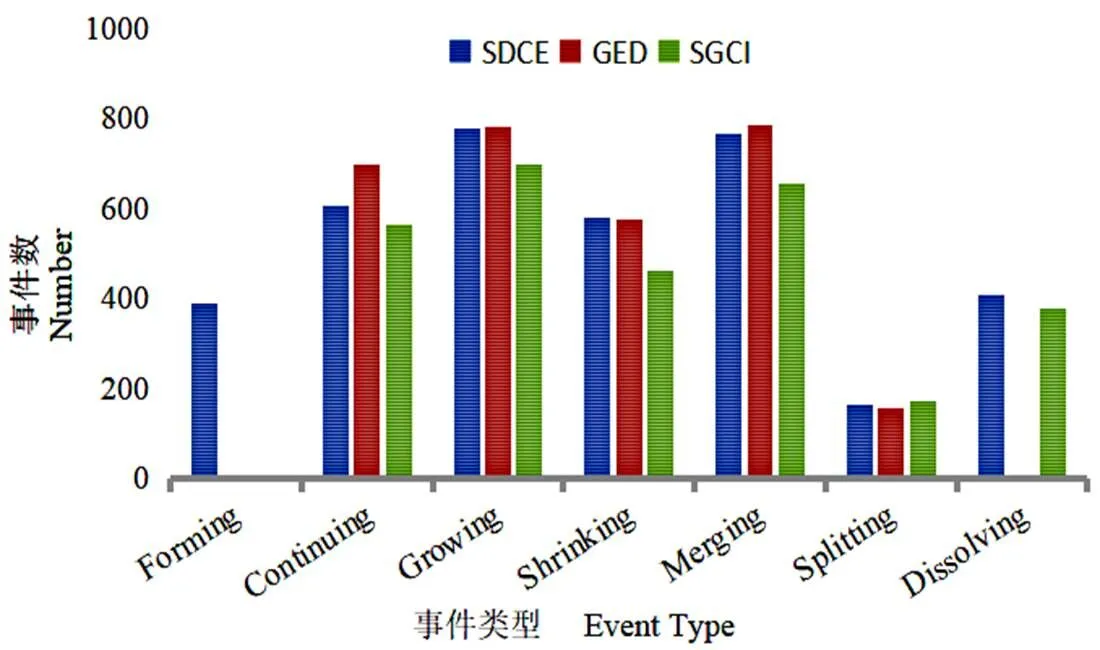
图4 HEP-TH数据集演化模型对比结果
3.2 HEP-TH数据集实验分析
为了进行对比试验,选用HEP-TH和波兰政治博客圈数据集。HEP-TH是高能物理理论引文网络,每个节点代表一篇论文,边代表引用关系,包含1993年1月至2003年4月共124个月的数据,共27770个节点,352807条边。选取了1994年1月至1994年11月的数据,共3268个节点,7100条边,将前后相邻两个月的数据划分到一个时间窗口,2月至10月的数据会同时被前后两个相邻时间窗口所采集,因此共划分为10个时间窗口。其中GED与SGCI的参数均选用论文中给出的最优参数。实验结果如图4所示。
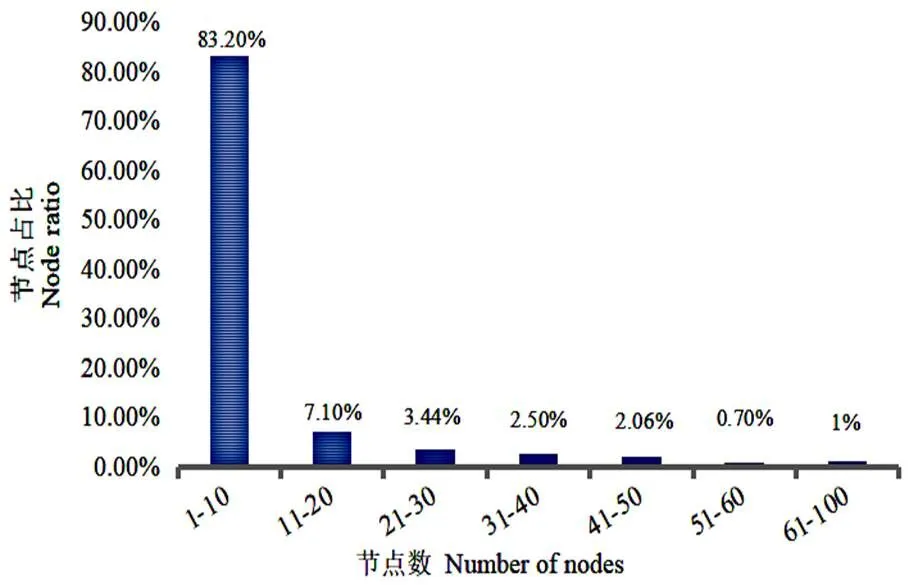
图5 HEP-TH数据集社区节点数分析图
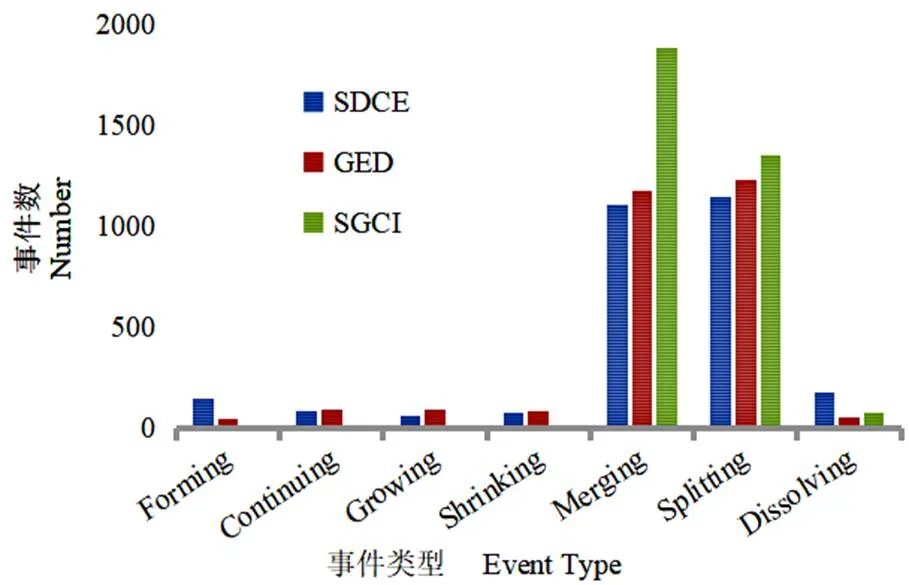
图6 波兰政治博客圈数据集演化模型对比结果
结果显示,对比GED与SGCI模型,提出的异同性演化分类模型可以较多地检测到各类演化事件,例如Forming和Dissolving。分析数据集可知,GED和SGCI模型的演化判别条件对小社区不敏感,例如Forming事件要求包含度小于10%,而如图5所示,HEP-TH数据集节点数小于10的社区个数占比为83.2%,要满足“包含度小于10%”的条件很困难,因此不容易检测到Forming事件。SGCI则是因为没有Forming这一演化类型。除此以外,在其他事件检测效果上与两类模型差别不大。以上可知,提出的演化分类模型在综合发现各类事件上有较强的优势,尤其对小社区同样有较好的检测结果。
3.3 波兰政治博客圈数据集实验分析
波兰政治博客圈是SGCI论文所使用的数据集,源于www.salon24.pl网站的博客数据,主题主要是政治性的,也包括少量其他主题。数据集包括26722名用户,285532条帖子和4173457条评论,时间跨度为2008年1月1日至2012年3月31日,每个月为一个时间窗,每个时间窗重叠15 d,共有104个时间窗。实验结果如图6所示。由图表可知,提出的模型对Forming和Dissolving事件的检测效果依然较好,在其他事件的检测效果上与另外两模型差别不大。其中SGCI检测到Merging及Spliting的事件数相对较高是因为SGCI部分事件类型与GED不相同,GED的Merging和Addition事件都被划分到了SGCI的Merging事件中,因此事件数相对较多;同样其Spliting事件包括Spliting和Deletion两类事件,数量也较多。因此独立看待每个事件类型,本文模型整体要优于GED及SGCI模型。
4 结语
本文提出了一种基于节点重要性评价指标p的差值吸收核心节点检测算法,该算法以节点p值为基础,对有边连接的节点进行一一比对,得到核心节点组成核心节点集。该方法不需要设定参数,时间复杂度较低,且寻找核心节点的准确率较高。以此为基础优化差异性公式,从相似性和差异性两方面对社区演化类型进行判定,提出了基于异同性的社区演化分类模型,并在HEP-TH和波兰政治博客圈数据集上进行了有效验证,结果表明本模型对Forming和Dissolving事件的检测结果要优于GED和SGCI分类模型。未来将对该演化分类模型进行优化,提高Merging及Spliting等事件的检测效果。
[1] Saganowski S. Predicting community evolution in social networks[C]//IEEE/ACM International Conference on Advances in Social Networks Analysis & Mining. Paris, France: IEEE, 2015
[2] 何婧.动态社交网络社区发现及演化分析[D].徐州:中国矿业大学,2019
[3] İlhan N, Öğüdücü GŞ. Feature identification for predicting community evolution in dynamic social networks [J]. Engineering Applications of Artificial Intelligence, 2016,55:202-218
[4] Bhat SY, Abulaish M. HOCTracker: Tracking the evolution of hierarchical and overlapping communities in dynamic social networks [J]. IEEE Transactions on Knowledge & Data Engineering , 2015,27(4):1013-1019
[5] Yin G, Chi K, Dong Y,. An approach of community evolution based on gravitational relationship refact oring in dynamic networks [J]. Physics Letters A, 2017,381(16):1349-1355
[6] Dhouioui Z, Toujani R, Akaichi J. Tracking dynamic community evolution and events mobility in social networks [J]. Encyclopedia of Social Network Analysis and Mining, 2017,978:73-80
[7] Bródka P, Saganowski S, Kazienko P. GED: The method for group evolution discovery in social networks [J]. Social Network Analysis and Mining, 2012,3(1):1-14
[8] Gliwa B, Saganowski S, Zygmunt A,. Identification of group changes in blogosphere[C]// Proceedings of 2012 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM). Piscataway, New Jersey, USA: IEEE, 2012:1201-1206
[9] 任卓明,邵凤,刘建国,等.基于度与集聚系数的网络节点重要性度量方法研究[J].物理学报,2013,62(12):128901-1-5
[10] Zygmunt A, KoLak J, Nawarecki E,. Determining life cycles of evolving groups [J]. Procedia Computer Science, 2014,35:1102-1111
[11] Bommakanti SASR, Panda S. Events detection in temporally evolving social networks [C]//2018 IEEE International Conference on Big Knowledge. Singapore: IEEE, 2018:235-242
The Community Evolution Classification Method on Similarity and Difference
LIU Ye-qiang1, WANG Lu1, YANG Sheng-bin2*, LIU Ya-qiong2
1.271018,2.271018,
The analysis of community evolution in dynamic network is one of the current research hotspots, which plays an important role in public opinion control, network marketing, personalized recommendation service and so on. This paper proposes a nonparametric core node detection algorithm based on the evaluation index of node importance, which is used to find the core nodes in the community nodes to form the core node set, and to judge the difference of community based on the core node set. Based on this, a classification model of community evolution based on similarities and differences is proposed. This model determines the evolution relationship and divides the evolution type from the two aspects of similarities and differences. Comparing the proposed classification model with GED and SGCI in hep-th and Polish political blogosphere data sets, the experimental results show that the proposed classification model is better than GED and SGCI classification model on the whole. Especially in the detection of forming and dissolving events, it can be sensitive to small communities, and can detect a variety of evolution types of small communities.
Cluster coefficient; core node detection; classification model of community evolution
TP301.6
A
1000-2324(2021)03-0489-07
2020-01-07
2020-03-21
国家自然基金重大研究计划(91746104);山东省重大科技创新工程项目(2019JZZY010706)
刘业强(2000-),男,本科,研究方向:智能信息处理. E-mail:364182723@qq.com
Author for correspondence. E-mail:ysb@sdau.edu.cn.
