SiO2地温计沸腾校正方法在高原地区的适用性分析

李义曼，庞忠和，罗霁，陈凯

1)中国科学院地质与地球物理研究所，页岩气与地质工程重点实验室，北京，100029； 2)中国科学院地球科学研究院，北京，100029； 3)中国科学院大学地球与行星科学学院， 北京，100049； 4)中国矿业大学(北京)，北京，100083

内容提要: 热储温度是开展地热资源研究的关键参数之一。地热勘查中常用基于地热流体化学和同位素数据的经验公式来评价没有钻孔或者钻孔未达到实际热储层情况下深部热储的温度。SiO2地温计应用最为广泛，对于发生了绝热沸腾的地热流体，通常采用Fournier等提出的100℃沸腾条件下的校正公式。考虑到海拔会影响沸点，本文从SiO2溶解度方程和温度相关性着手，评价了SiO2地温计沸腾校正方法在高原地区的适用性。结果表明Fournier(1977)及Fournier 和 Potter(1982)提出的100 ℃条件下SiO2绝热沸腾校正方法得到的误差分别为2.4%和1.1%，可以代表深部热储温度，即SiO2地温计沸腾校正方法在高原地区也是适用的。

地热能是一种分布广泛，资源潜力巨大、安全稳定且利用系数较高的可再生清洁能源(汪集暘等，2020)。近年来，其开发利用逐渐规模化，特别是北方地区的冬季供暖。其中深部热储温度是开展地热资源研究的关键参数之一，是地热资源类型划分、开采潜力评价以及开发利用模式选择的重要依据，也是开展地热系统成因模式研究的重要内容(袁利娟等，2020)。实际工作中，特别是勘查的初期阶段，很多地方没有钻孔或者钻孔未达到实际热储层，这种情况下就可以利用地热流体化学和同位素数据来估算深部热储温度(庞忠和等，2013)，即流体地温计，即利用地热水的化学组分，如SiO2、Na/K值等，以及气体组分和同位素等与温度的相关性，计算热储的温度。目前，流体地温计包括经验公式地温计和基于化学热力学、动力学的理论地温计，应用较广的包括SiO2地温计、阳离子地温计、气体地温计、同位素地温计和多矿物组合地温计等。SiO2地温计是根据硅矿物溶解度建立起来的方法，适用温度范围比较大，精度较高，应用广泛，如罗璐等(2019)和李泓泉等(2020)将其分别应用于关中盆地和冀西北蔚县盆地进行深部热储温度估算。但有些情况下须考虑具体的应用条件，如绝热沸腾地温计主要针对100 ℃条件下发生沸腾作用时，利用地表采集到的地热水样品SiO2数据计算热储温度。

我国高温地热资源主要分布于青藏高原，该区海拔普遍高于3000m，导致水的沸点也发生变化。在实际工作中，通常在井口或者泉口采集地热水样品。这种情况下，深部地热流体上升至地表过程中可能会发生沸腾，一部分水将以蒸汽形式散失掉，进而导致剩余地热流体中SiO2的浓度增大，需要用绝热沸腾地温计来扣除该影响。但在高海拔地区，水的沸点已经不是100 ℃了，直接利用现有SiO2绝热沸腾公式计算可能会产生误差或者错误，所以需要系统评价海拔高程对SiO2绝热沸腾地温计的影响。本文从SiO2溶解度方程和海拔对沸点影响入手，评价了不同沸点条件下，现有绝热沸腾地温计得到的热储温度与实际热储温度的差异，并计算了误差，可为不同海拔地区的地热水样品选择合适的地温计方法提供科学依据。

1 SiO2地温计

1.1 SiO2溶解度及常用地温计

水中SiO2浓度对温度的变化反应灵敏，这也是其成为地热系统中被广泛应用的经验地温计的主要原因。自然界中常见的SiO2矿物包括石英、无定型SiO2、玉髓和方石英等。由于不同矿物形态的SiO2在水中的溶解度不同，在利用SiO2地温计时一定要根据实际地热系统条件选择合理的方法，常用的有石英地温计、玉髓地温计和无定型SiO2地温计。

研究表明，基于纯水中石英溶解度实验数据，石英地温计在利用井口地热水样品SiO2浓度估算热储温度方面是可靠的(White et al.,1956; Morey et al., 1962; Fournier and Potter, 1973a; Fournier and Truesdell, 1974; Gunnarsson and Arnórsson, 2000; Verma, 2000)，但对热泉样品应用此地温计时，给出的结果可能存在误差。这是由于上升过程中可能发生绝热沸腾和稀释作用，导致石英平衡被破坏，达到平衡的可能是其他SiO2矿物，如玉髓或者无定型SiO2。

石英地温计是基于气—液两相饱和线的纯水中石英溶解度实验数据建立的，对高温(如温度大于330 ℃)地热卤水不适用。目前已有实验数据包括300 ℃以上和300 ℃以下两方面(图1)。基于这些数据，不同学者建立了相应的石英溶解度方程，常用的包括以下4个(表1)：

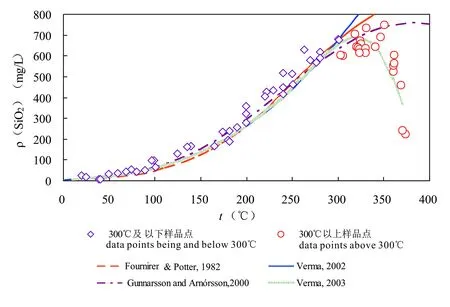
图 1 石英溶解度随温度变化的实验数据及拟合曲线(修改自Verma, 2008)Fig. 1 Experimental data of quartz solubility with temperatures and the fitted curve (modified from Verna, 2008)

表1 石英溶解度方程统计表Table 1 Summary of quartz solubility equations

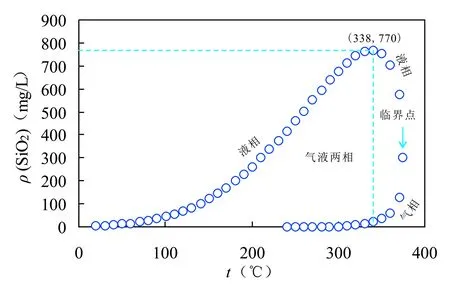
图 2 石英溶解度随温度变化曲线(修改自Giriarso et al., 2017)Fig. 2 Quartz solubility variations with temperature (modified from Giriaso et al., 2017 )

(1)Verma于2003年建立的1/(T/K)与P/(MPa)之间的一元二次方程(式1)；

(2)Verma于2002年建立的lg[ρ(SiO2)/(mg/L)]与温度之间的相关关系(式2)；

(3)Gunnarsson和Arnórsson于2000年提出的lg[C(SiO2)/(mol/L)]与温度之间的相关关系(式3)；

(4)Fournier和Potter于1982年提出的ρ(SiO2)/(mg/L)与温度之间的相关关系(式4)。

根据图1，当温度小于300 ℃时，方程(2)对石英溶解度曲线的拟合更好一些；多项式方程(3)(Fournier and Potter, 1982)和(4)(Gunnarsson and Arnórsson, 2000)的有效适用温度可分别达350 ℃和330 ℃。但实验数据表明，由于水的相态发生变化，温度大于320℃时液态水中石英溶解度发生降低，而这三个方程(方程2、3和4)都没有考虑此问题，所以无法拟合超过320 ℃的实验数据，即当温度超过320 ℃时，这3个方程拟合效果很差，不能真实反映出SiO2的浓度和温度的相关性。方程(1)基于化学热力学原理，可以更好的拟合水达到超临界态(t=374 ℃)以前的石英溶解度实验数据。

研究表明，当温度达到338 ℃时，石英的溶解度可达770 mg/L，而在超临界温度时，其溶解度仅为300 mg/L(图2)。所以，对于发生了传导冷却的地热流体，当其中SiO2含量高于300 mg/L 时，热储温度存在两种情况，低于或者高于338 ℃。 当温度大于230 ℃时，石英的溶解沉淀会快速发生，所以利用SiO2地温计计算温泉的热储温度时，得到的结果不会高于230 ℃(Fournier, 1973b; Rimstidt and Barnes, 1980)。

玉髓是石英和单斜硅石的混合物，由非常细小的晶体组成，由于其非常细小，所以较石英更易溶于水中(Heaney and Post，1992；Walther and Helgeson, 1977)。Fournier和Rowe于1966年发表了125℃～255 ℃范围内7个玉髓溶解度的实验数据，Fournier于1973年又补充了92 ℃ ～259 ℃范围内的6个数据点，1977年Fournier发表了玉髓地温计方法(Gíslason et al., 1993)。Arnórsson于1975年总结出冰岛地区与玉髓达到平衡的地热水的温度一般低于180 ℃，并于1983年基于已有的玉髓溶解度数据以及冰岛地热水温度与二氧化硅的关系，建立了25 ℃ ～180 ℃范围内玉髓溶解度的经验公式(Arnórsson et al.，1983)。该公式(式5)与实测数据吻合较好，其中t的单位是℃，ρ(SiO2)的单位是mg/L。但冰岛地区的热储岩性以火成岩为主，如玄武岩，由于低温条件下石英的溶出和沉淀速率不一致，地热水一般与玉髓平衡，所以一般中低温地热系统，建议采用玉髓地温计。但在沉积岩地区，其可溶出的矿物较火成岩少很多，所以即便温度低于100 ℃，地热流体也可能与石英达到了平衡。

(5)

相比石英和玉髓地温计，无定型SiO2地温计应用相对较少。无定型SiO2的溶解度较大，碳酸盐型地热水中SiO2的含量通常受无定型SiO2的溶解度控制(Arnórsson和Barnes, 1983)。

1.2 SiO2地温计绝热沸腾校正方法

当热储温度超过100 ℃时，地热流体从深部热储上升至地表过程中可能会发生绝热沸腾(adiabatic boiling)，水气分离导致一部分含CO2和H2S等气体的蒸汽散失掉，使剩余地热流体中溶质(SiO2)的浓度会随散失掉的蒸汽比例增加，同时pH值升高。直接利用地表采集到的地热水样品中的SiO2含量进行热储温度计算时会出现高估的问题。针对这种情况，Fournier(1977)、Fournier和Potter(1982)以及Arnórsson等(1998)提出了深部地热流体绝热沸腾到100 ℃条件下，利用地表采集到的地热水中SiO2浓度计算深部热储温度的地温计方法，详见下式(6)(Fournier， 1977)、式(7)(Fournier和 Potter, 1982)、式(8)(Arnórsson et al., 1998)。

(6)

(7)

(8)

式(6)适用的温度范围是25 ℃～900 ℃；式(8)适用的温度范围是0 ℃～350 ℃。

这三种考虑了蒸汽散失影响的SiO2地温计均针对地热流体在100 ℃条件下发生绝热沸腾的情况。但在实际生产中，存在很多分布于高海拔地区的高温地热系统，当地的沸点一般都小于100 ℃。对于这类地区，直接利用目前已有的SiO2地温计绝热沸腾校正方法，给出的结果可能存在误差；此外，由于这类系统多发生了蒸汽散失，直接利用在地表采集到的气体样品及气体地温计进行热储温度估算，也可能产生误差。但这对热储温度的影响到底有多大，是否需要校正，还不清楚。所以需针对这类系统，详细探讨海拔的影响。

2 海拔对沸点的影响

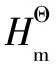
(9)

(10)

(11)

所以，利用式(11)可计算不同海拔条件下水的沸点，如图3所示，可见对于海拔3000 m以上的地区，沸点可低于90.1 ℃，变化可大于10 ℃。

图3 不同海拔条件下水的沸点变化图Fig. 3 Boiling point variations with various altitudes

3 SiO2地温计绝热沸腾校正方法 在高原地区的适用性分析

为了方便讨论SiO2地温计绝热沸腾校正方法在高原地区的适应性，我们假设实际热储温度为150.0 ℃。利用石英溶解度方程(Verma, 2000)确定该温度条件下地热水中SiO2含量为120.0 mg/L。根据表1及饱和蒸气压表(表2)，可得出不同海拔条件下水发生沸腾时，单位质量饱和蒸汽(Hv)和饱和水(Hl)的热焓值，如表2中所示。当热储温度为150 ℃时，单位质量饱和水的热焓值是632.3 kJ/kg。我们可计算出在不同海拔条件下发生绝热沸腾时，散失掉的蒸汽比例，见表3。

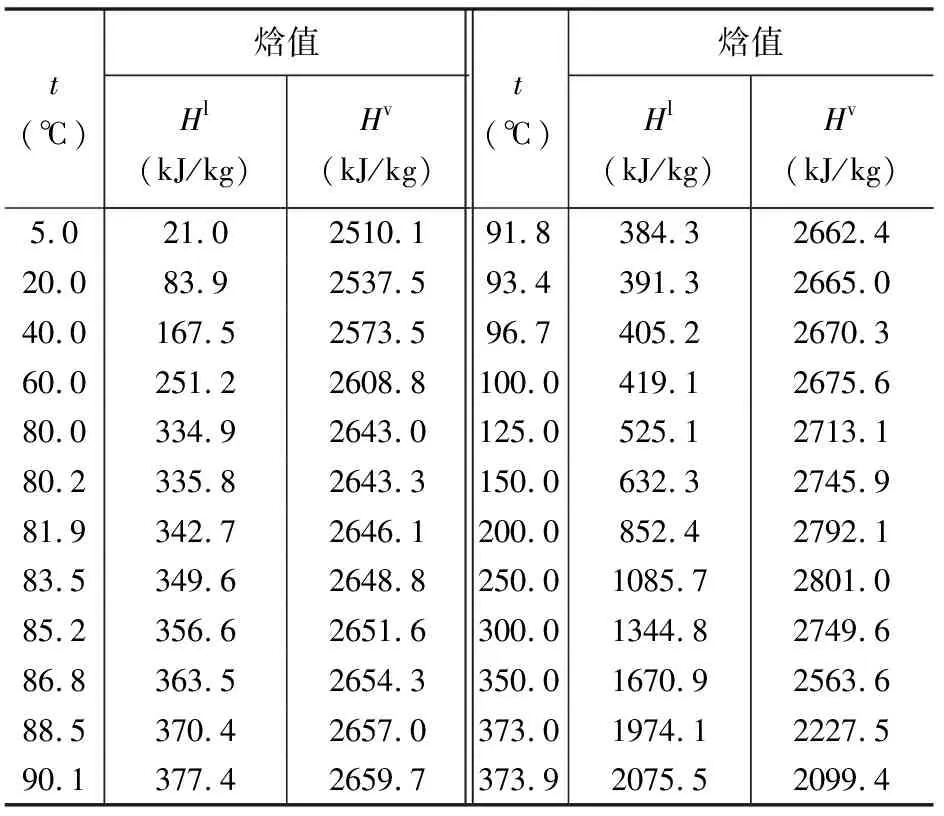
表2 部分温度条件下饱和蒸气压表Table 2 Saturated steam table of temperatures from 5 to 373.94 ℃

表3 不同沸点条件下单位质量饱和蒸气压和饱和水焓值及蒸汽比例Table 3 Saturated vapor pressure and saturated water enthalpy per unit mass and vapor ratio at different boiling points

根据表4，当海拔为0 m时，水的沸点是100.0 ℃，若热储温度为150.0 ℃，则地热水上升至地表时散失的蒸汽比例为9.4%，采集到的地热水样品中SiO2含量大约为132.5 mg/L。利用1.2节中提到的三个SiO2绝热沸腾校正公式(式6、7和8)，计算得出热储温度分别为146.4 ℃、148.4 ℃和136.9 ℃。前面两个估算的温度与实际热储温度基本一致，误差分别为2.4%和1.1%，利用式(8)得到的温度略偏低，误差为8.7%，如表5所示。当海拔为3000 m时，水的沸点变成90.1 ℃，此时地热水上升至地表时散失的蒸汽比例增加为11.2%，地表采集到的地热水样品中SiO2含量大约为135.1 mg/L，利用SiO2地温计绝热沸腾校正方法得到的热储温度分别是147.4 ℃,149.4 ℃和138.0 ℃。与海拔为0 m时类似，式(6)和(7)估算得到的温度与热储温度基本一致，式(8)得到的温度偏低。误差计算结果表明(表4)，对于海拔6000 m以下地区，Fournier(1977)提出的校正方法计算得到的热储温度误差为1.1%～2.4%，且随海拔增加误差反而降低；Fournier 和 Potter(1982)提出的校正方法给出的误差为0.1%～1.1%，在海拔4000～4500m时，误差最小；Arnórsson等(1998)提出的校正方法误差为7.3%～8.7%，且随海拔增加误差降低。总的来说，利用Fournier(1977)及Fournier 和 Potter(1982)提出的100 ℃条件下SiO2地温计绝热沸腾校正方法得到的温度基本可以代表热储温度，误差分别小于2.4%和1.1%，即海拔对其影响可以忽略不计。其中Fournier 和 Potter(1982)方法得到的结果最接近实际热储温度；但Arnórsson等(1998)提出的校正方法得到的温度结果明显偏低11.0～13.0 ℃，误差偏大。

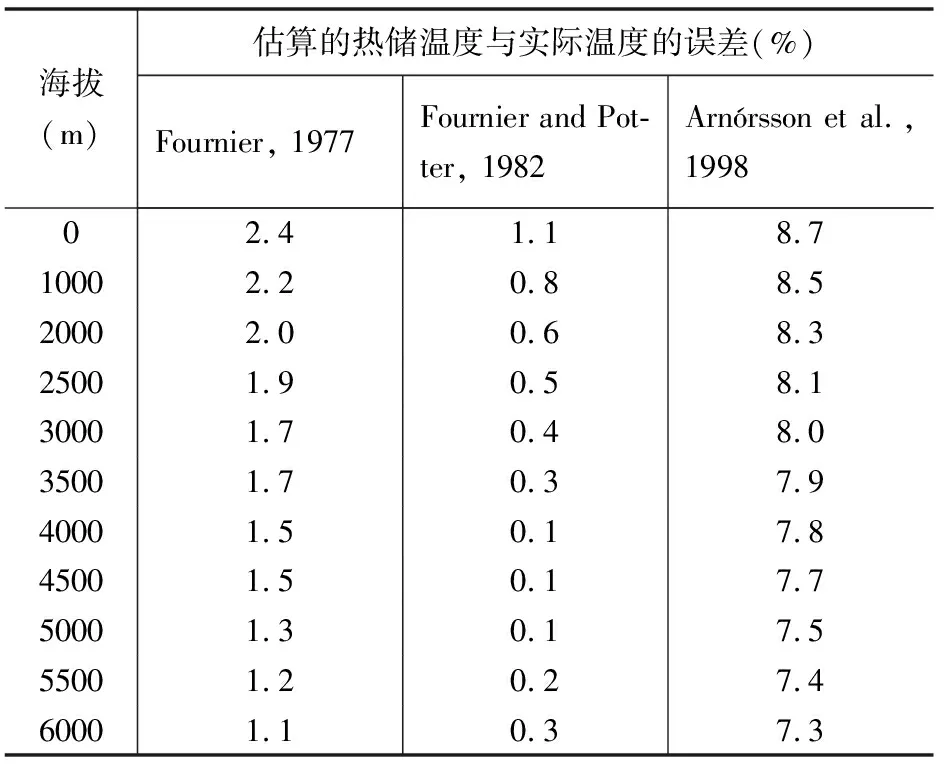
表4 不同海拔下SiO2地温计绝热沸腾校正方法计算的 热储温度与实际热储温度的误差

综上，得出以下结论，虽然不同海拔条件下水的沸点不同，从海拔为0 m到海拔为6000 m，水的沸点从100.0 ℃降低至80.2 ℃，减小了约19.8 ℃，但利用Fournier(1977)及Fournier 和 Potter(1982)提出的100.0 ℃条件下SiO2地温计绝热沸腾校正方法得到的温度可以代表热储温度，其中Fournier 和 Potter(1982)提出的校正方法更能反映深部热储的温度。

4 结论

不同海拔高程条件下沸点计算及热储温度评价结果表明，对于0～6000m 范围内的海拔条件，水的沸点从100.0 ℃降低至80.2 ℃，但Fournier等提出的校正公式得到的结果与实际温度误差较小，可以代表热储温度，也就是说海拔对现有绝热沸腾地温计计算结果的影响可以忽略不计。其中Fournier 和 Potter(1982)提出的校正方法更能反映深部热储的温度。

致谢：中国科学院青藏高原研究所赵平研究员对本文中提出的问题及如何评价海拔对热储温度影响给予了很多建设性建议；杨峰田副教授、章雨旭研究员和另一位审稿专家提供了宝贵的修改意见，在此一并致以衷心的感谢！

参 考 文 献／References

(The literature whose publishing year followed by a “&” is in Chinese with English abstract; The literature whose publishing year followed by a “#” is in Chinese without English abstract)

邝生鲁, 梁启勇, 毛静萍. 1993. 沸点与海拔高度关系式的导出. 武汉化工学院学报，15(3)：78～81.

李泓泉,张树胜,谢明忠,周江,周建飞,贾立新,郝星波,任建帅,刘永平,于丹丹.2020.冀西北蔚县盆地地热资源赋存特征及勘查开发方向.地质论评,66(4):919～931.

罗璐,朱霞,何春艳,毛翔,许振华,汪新伟,朱咸涛.2019.陕西咸阳地热田地热流体成因研究.地质论评,65(6):1422～1430.

庞忠和, 杨峰田, 罗璐.2013. 地热田储层温度的确定方法. 见：丁仲礼.主编.固体地球科学研究方法. 北京：科学出版社:219～242.

汪集暘, 庞忠和, 孔彦龙, 程远志, 罗霁. 2020. 我国地热清洁能源供暖产业现状与展望. 科技促进发展, 16(3)：294～297.

袁利娟, 孔祥军, 高剑, 沈鹏飞, 何云成, 冯浩, 李文, 郝伟俊. 2020. 北京市延庆地热田成因模式. 地质论评, 66(4)：933～940.

Arnórsson S, Gunnlaugsson E, Svavarsson H. 1983. The chemistry of geothermal waters in Iceland, llI. Chemical geothermometry in geothermal investigations. Geochimica et Cosmochimica Acta, 47: 567～577.

Arnórsson S, Barnes I. 1983. The nature of carbon dioxide waters in snaefellsnes, western iceland. Geothermics, 12(2～3), 171～176.

Arnórsson S,Andrésdóttir A, Gunnarson I, Stefánsson A. 1998. New calibration for the quartz and Na/K geothermometers-valid in the range 0～350 ℃. In: Proceedings of the Geosciences Society of Iceland Annual Meeting, April,1994: 42-43 (in Icelandic).

Fournier R O.1973a.An equation correlating the solubility of quartz in water from 25℃ to 900 ℃ at pressure up to 10,000 bars. Geochimica et Cosmochimica Acta, 46:1969～1973.

Fournier R O.1973b. Silica in Thermal Waters: Laboratory and Field Investigations. In: Proceedings, International Symposium on Hydrogeochemistry and Biogeochemistry, Tokyo, 1970: v. 1, Hydrogeochemistry. Washington, D. C.: Clark: 122～139.

Fournier R O.1977.Chemical geothermometers and mixing models for geothermal systems. Geothermics, 5: 41～50.

Fournier R O, Potter R W. 1982. A revised and expanded silica (quartz) geothermometer. Geothermal Resource Council Bulletin, 11: 3～12.

Fournier R O, Truesdell A H. 1974. Geochemical indicators of subsurface temperature, part II. Estimation of temperature and fraction of hot water mixed with cold water. US Geological Survey Journal of Research, 2(3): 263～270.

Giriarso J P M, Husni Thamrin, Eben Ezer Siahaan. 2017. Enhancement of silica—enthalpy mixing model to predict enthalpy of geothermal reservoir. In: Proceedings, 42nd Workshop on Geothermal Reservoir Engineering. Stanford University, Stanford, California, February 13～15, 2017 SGP-TR-212.

Gunnarsson I, Arnórsson S. 2000. Amorphous silica solubility and the thermodynamic properties of H4SiO4in the range 0 ℃ to 350 ℃ at P sat. Geochimica et Cosmochimica Acta, 64:2295～2307.

Gislason S R, Heaney P J, Veblen D R, Livi K J T. 1993. The difference between the solubility of quartz and chalcedony: the cause? Chemical Geology, 107(3～4):363～366.

Heaney P J, Post J E. 1992. The widespread distribution of a novel silica polymorph in microcrystalline quarts varieties. Science, 255: 441～443.

Kuang Shenglu, Liang Qiyong, Mao Jinpin. 1993&. The presentation of the relation between boiling point and altitude. Journal of Wuhan Institute of Chemical Technology, 15(3): 78～81.

Li Hongquan, Zhang Shusheng, Xie Mingzhong, Zhou Jiang, Zhou Jianfei, Jia Lixin, Hao Xingbo, Ren Jianshuai, Liu Yongping, Yu Dandan.2020&.The occurrence characteristics and exploration and development direction of geothermal resources in Yuxian Basin, northwest Hebei Province.Geological Review,66(4):919～931.

Luo Lu, Zhu Xia, He Chunyan, Mao Xiang, Xu Zhenhua, Wang Xinwei, Zhu Xiantao.2019&.Study on the genesis of geothermal fluid in Xianyang geothermal field.Geological Review,65(6):1422～1430.

Morey G W,Fournier R O, Rowe J J. 1962. The solubility of quartz in water in the temperature interval from 29 to 300 ℃. Geochimica et Cosmochimica Acta, 26: 1029～1043.

Pang Zhonghe, Yang Fengtian, Luo Lu. 2013#. Evaluation methods of reservoir temperature in geothermal field. In: Ding Zhongli. eds. Study Methods for Solid Earth Sciences. Beijing: Science Press: 219～242.

Rimstidt J D. 1997.Quartz solubility at low temperatures. Geochimica et Cosmochimica Acta, 61(13):2553～2558.

Rimstidt J D, Barnes H L. 1980.The kinetics of silica—water reaction. Geochimica et Cosmochimca Acta, 44: 1683～1699.

Verma M P. 2000. Chemical thermodynamics of silica: a critique on its geothermometers. Geothermics, 29: 323～346.

Verma M P. 2002. Geochemical techniques in geothermal development. In: Chandrasekharam D, Bundschuh J. eds. Geothermal Energy Resources for Developing Countries. The Netherlands: Swets & Zeitlinger Publishers: 225～251.

Verma M P. 2003. QrtzGeotherm: a computer program for the quartz solubility geothermometer in moderately saline brines up to 370 ℃. Geothermal Research óCouncil Transactions, 27:341～345.

Verma M P. 2008. Qrtzgeotherm: an activex component for the quartz solubility geothermometer. Computers & Geosciences 34(12), 1918～1925.

Walther J V, Helgeson H C. 1977. Calculation of the thermodynamic properties of aqueous silica and the solubility of quartz and its polymorphs at high pressures and temperatures. American Journal of Sciences, 277:1315～1351.

Wang Jiyang, Pang Zhonghe, Kong Yanlong, Cheng Yuanzhi, Luo Ji. 2020&.Status and prospects of geothermal clean heating industry in China. Technology for development, 16(3):294～297.

White D E, Brannock W W, Murata K J. 1956. Silica in hot-spring waters. Geochimica et Cosmochimica Acta， 10: 27～59.

Yuan Lijuan, Kong Xiangjun, Gao Jian, Sheng Pengfei, He Yuncheng, Feng Hao, Li Wen, Hao Weijun.2020&.Genetic model of the Yanqing geothermal field, Beijing. Geological Review, 66(4):933～940.