基于注意力与长短期记忆网络的变压器代理模型

金 亮 冯裕霖 曹佳豪 王艳阳

基于注意力与长短期记忆网络的变压器代理模型

金 亮1,2冯裕霖1曹佳豪1王艳阳1

（1. 天津市电工电能新技术重点实验室（天津工业大学），天津 300387； 2. 省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学），天津 300130）

由于需要考虑换能效率、噪声、体积和质量等因素，电力变压器的设计参数和性能数据往往十分复杂，因此，如何建立变压器代理模型是亟需解决的问题。采用代理模型的优化算法（SBO）能有效解决数值模拟直接优化耗时长的问题。本文用深度学习建立变压器设计参数和性能数据的代理模型，实现变压器性能优化目标的高精度预测，有效降低变压器性能分析与优化所需时间。首先基于长短期记忆网络（LSTM）的深度学习模型，建立非晶合金变压器各个参数间的非线性映射，并加入注意力机制来增强模型的预测效果。最后，通过有限元仿真实验对提出的深度学习代理模型进行验证，并与其他常用的代理模型进行比较，证明了注意力机制与长短期记忆网络代理模型在预测精度方面的优越性。

非晶合金变压器；有限元方法；代理模型；深度学习；长短期记忆网络；注意力

0 引言

电力变压器作为电网中能量转换、传输的核心，其性能直接关系到电力系统运行的可靠性和经济性。随着我国经济水平的不断提高，人们对于电力能源的需求日益增加。由于人类生产生活对供电量的需求不断增长，对电力变压器的设计、制造和优化也有了更高的要求。电力变压器优化设计作为一个多学科设计优化问题（multidisciplinary design optimization, MDO），通常由电、磁、热、机械和力学等多个物理场组合而成。在复杂的工作环境下，受线路条件、空气、温度等影响，变压器内部与外部的相互作用加剧，很难找到设计参数与优化目标之间的变化规律。因此，如何针对电力变压器庞大而复杂的非线性数据进行优化设计成为一个值得关注的问题。

传统变压器设计方法主要包含磁场分析法和解析法[1]。磁场分析法和解析法因与经典电磁理论结合紧密被广泛应用。传统的变压器设计在寻求本系统最优解的时候，很少考虑不同部件之间相互影响的问题。按照这种设计模式得到的结果往往只是局部最优，而非全局最优。随着有限元计算与仿真技术的发展，计算机仿真技术广泛应用于实际产品设计中，通过有限元软件对变压器系统进行全方位数字化建模与仿真，再辅之以物理样机的验证形式，从而加快设计进度，降低设计成本，减少设计反复等。但是复杂电力变压器系统涉及机械、电气、力学等多学科领域，设计变量、目标函数和约束边界众多，模型的迭代次数和计算时间会随着数据维度和物理场的增加呈现几何级数的增长[2]。变压器优化设计问题通常采用现代启发式优化算法进行全局寻优，比如遗传算法[3]、模拟退火算法[4]、粒子群算法[5]和差分进化算法[6]等。这些优化算法能够获得理想结果，但需要的仿真次数多，计算时间长，影响电力变压器的设计周期。

基于代理模型的优化算法（surrogate-based optimization, SBO）只需少数样本数据即可建立拟合目标值与输入变量之间数学关系的代理模型，再借助现代启发式优化算法快速寻找到全局最优值[7]。该算法可以在很大程度上减少仿真次数，适合有限元仿真和电力变压器性能预测等高计算成本的应用场合[8]。代理模型主要包括克里金模型[9]、神经网络模型[10]、径向基函数[11]、支持向量回归模型[12]等。常用的代理模型面对愈加复杂的变压器优化设计问题，预测效果并不能令人满意[13]。伴随深度学习模型的兴起，深度学习模型作为一种新形式代理模型受到广泛关注。深度学习模型具有结构简单、映射能力强的特点，一旦结构的初值被赋予后，训练过程则可自动完成。邵振峰开发一种基于深度学习的工作流程来绘制森林生物估计量，其预测精度和拟合程度均超过其他模型[14]。Gao开发了一种基于深度学习的代理模型以取代与最大传输能力（total transfer capability, TTC）相关的耗时的微分代数计 算[15]。Barmada S. 提出了使用两种不同的卷积神经网络模型进一步减少电磁设备优化过程中的总体计算时间[16]。综上所述，深度学习相比传统的代理模型方法，通过堆叠多层神经网络自动提取深层次特征，大大降低了对算法设计人员经验的依赖，增强了预测结果的准确度。

本文考虑到长短期记忆网络（long-short term memory, LSTM）对复杂数据进行深层次特征提取的特点，提出一种新的电力变压器性能预测方法。首先，本文通过搭建非晶合金电力变压器模型，对变压器中电磁、力学等多物理场进行仿真分析。然后，基于LSTM模型建立一种基于Attention-LSTM的变压器的代理模型，通过注意力（Attention）机制提高代理模型的预测精度，并且有效降低代理模型训练所需的时间。最后，采用有限元方法对变压器进行仿真，验证算法的可靠性。

1 基于深度学习的代理模型

1.1 循环神经网络工作原理

循环神经网络（recurrent neural networks, RNN）是一种具有记忆功能的深度神经网络，可用于处理具有前后非独立特征的序列数据，是深度网络模型之一。单个隐藏层的循环神经网络结构如图1所示。图1中，x、s、o分别为时刻输入层、隐藏层、输出层的值，为输入层到隐藏层的权重矩阵，为输入层到隐藏层的权重矩阵，为隐藏层至其自身的权重矩阵。虽然RNN可以很好地解决性能参数预测问题，但是循环神经网络存在梯度下降快、很难训练、无法收敛到最优解等问题。而LSTM有选择性地保存信息，并且对于复杂数据可提高预测效率，往往表现出比RNN更好的预测效果。

1.2 长短期记忆神经网络模型

传统代理模型的共同特点是将复杂数据作为模型的输入，通过预处理等方法选择主要特征来最大化地保证代理模型的精度。在处理后，复杂数据中的原有特征常常会出现缺失的情况。LSTM是一种特殊的循环神经网络结构，只要有适当的权重矩阵和足够的网络单元，就可以在保证合适精度的前提下，作为代理模型使用。

图1 循环神经网络结构

LSTM是基于RNN改进的一种算法，将RNN中的神经元替换为一个拥有记忆能力的线性神经元即为LSTM模型。在LSTM记忆神经元内部加入遗忘门、输入门和输出门，目的是实现保存、写入和读取的特殊功能，这些门都是逻辑单元，根据输入序列，所有记忆单元被连接，解决了循环神经网络中的梯度下降快、无法收敛到最优解等问题，在性能参数预测中取得了很好的效果，LSTM模型结构如图2所示。

图2 单个隐藏层的LSTM模型结构

计算节点由输入门、输出门、遗忘门和cell组成，其中cell是计算节点核心，用以记录当前时刻状态，根据图2描述记忆模块中各单元的具体运算关系如下。

遗忘门：使模型有选择性地遗忘一些数据。

输入门：管理模型新输入信号数据。

输出门：使模型可以有选择性的输出结果。

更新神经元的记忆状态：由遗忘门保留的记忆数据和输入门输入的数据组成。

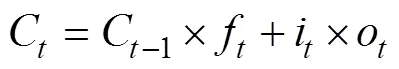
模型总输出：分别输出到下个神经元部分和输出到下一层网络对应位置。

式中：为外界的输入数据；为上一个神经元需要遗忘的数据；为神经元新输入的数据；为该神经元对外的输出结果；为神经元更新后的记忆状态；为该模型的总输出；为sigmoid函数；tanh为双曲正切函数；f为遗忘门，决定哪些历史信息从细胞状态中丢弃，控制是否遗忘；a为输入门，负责处理当前序列位置的输入，决定哪个状态将被更新；o为输出门，决定输出部分单元状态；fio分别为与x和h-1对应的遗忘门、输入门、输出门转换的权重矩阵；fa、o分别为遗忘门、输入门、输出门转换的偏移向量。

1.3 注意力机制

注意力机制通过对模型输入变量进行计算，赋予输入变量不同的权重，对关键影响因素赋予更高的权重，以帮助模型做出更准确的判断。同时，由于Attention机制可以高度并行的计算，因此计算时间几乎不受影响。因此，在LSTM模型中引入Attention机制如图3所示，突出了重要因素，提高了预测效果。

图3 Attention机制结构

式中：为节点对输出的注意力概率权重；为第个输入元素对应的隐藏层状态值；为输入变量的个数。

通过计算每个隐层向量的得分，评估向量对输出结构的影响程度，分析各个隐藏层数据的相关程度，计算出每一个输入数据对输出结果的注意力概率权重，计算公式为

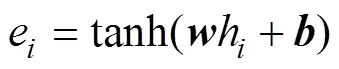
式中：为输出结果与隐藏层数值的相关程度；、分别为权重矩阵和偏置向量。

2 电磁仿真计算与代理模型构建

2.1 非晶合金变压器模型

本文选取一台小型非晶合金变压器作为研究对象，通过在铁心上绕制励磁绕组，制成一个单相非晶合金变压器样机，有限元方法建立的非晶合金变压器的三维仿真模型，如图4所示。其主要参数见表1。

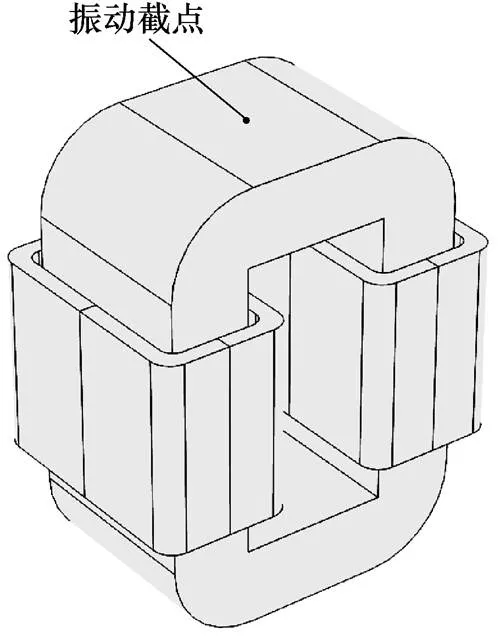
图4 变压器三维仿真模型

表1 非晶合金变压器参数

变压器的设计需考虑体积和振动等问题。变压器的大小主要由磁心尺寸确定，磁心的尺寸取决于窗口面积和磁心有效截面积的乘积，用p来表示。

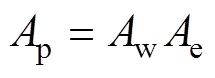
式中：w为窗口面积；e为磁心有效截面积。

式中：1为一次侧有效值电压；p为匝数；AC为磁通密度；为磁通量；f为波形因数。

设绕组的电流密度为，导线的截面积1/。令窗口面积利用系数为w。一次、二次绕组的有效值电流分别为1、2，绕组面积全部利用时，有

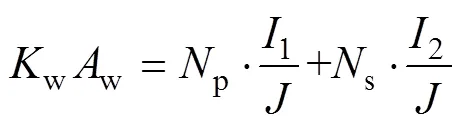
由式（11）推出

式中：2为二次侧有效值电压；为频率。

式中：1、0分别为一次侧、二次侧功率；为变压器效率。

由式（13）分析可知变压器大小受到铁心长度、窗口高度、窗口宽度、线圈匝数和线圈导线截面积等多个参数影响，并且是非线性相关的。

通常情况下，非晶变压器铁心区域中交变磁场产生感应电场，该电场产生感应电流即涡流，而工频交流激励下，位移电流可忽略不计，麦克斯韦方程组可表示为

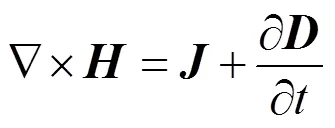
式中：为磁场强度（A/m）；为电场强度（V/m）；为磁通密度（T）；为电流密度（A/m2）。

引入磁矢位定义矢量磁位，可得到求解铁心电磁场的微分方程

在交变磁场作用下，非晶铁心产生磁致伸缩效应为

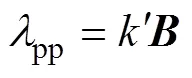
变压器铁心内某点的振动方程表示为

式中：为质量矩阵；为阻尼矩阵；为刚度矩阵；为节点位移；主要包括麦克斯韦力和磁致伸缩力。铁心振动主要来自于磁致伸缩效应，采用加速度作为分析铁心振动的研究目标。由上面分析可知变压器铁心振动中的电磁计算是变压器内的电、磁和力学相互之间高度耦合问题，输入与输出之间的关系具有非线性的特性。

2.2 样本建立

本文选取5个结构参数作为输入变量{1,2,3,4,5}，每个变量各取4个值，变压器铁心体积、振动加速度z为输出变量，采用全面试验设计方法来获取样本数据，这样可以获得具有很强代表性的样本数据点，且满足回归建模所需的样本数量。经有限元方法计算得到结构参数与目标函数的数据共1 024组。5个结构参数的取值水平见表2。

表2 5个结构参数的取值水平

采用归一化方法将有限元软件计算得到的样本数据集的输入变量归一化为均值为0、方差为1的数据集。利用交叉验证的方法将归一化后数据集划分为训练数据集和测试数据集，其占比分别为80%和20%。

2.3 预测评价指标

选取平均绝对百分误差（mean absolute percentage error, MAPE）作为LSTM模型预测效果的评价指标，MAPE值越小表示代理模型的精确度越高，即

2.4 有限元计算结果与实验对比

为验证非晶合金铁心振动有限元计算结果的准确性，采用振动测量分析仪对非晶变压器小型样机的铁心振动加速度进行测量。三轴加速度传感器探头粘贴在样机上部与模型参考相近处，将供电频率设置为50Hz，调节励磁电流使非晶变压器铁心在其运行稳定时由振动分析仪测量并记录振动数据。变压器样机的振动测量采用振动噪声分析仪作为信号采集装置，具体实验装置如图5所示。

图5 变压器样机振动实验装置

非晶铁心样机的振动加速度实验测量结果与有限元仿真计算结果分别如图6和图7所示。实测振动数据为：轴振动加速度峰值约为1m/s²；轴振动加速度峰值约为0.27m/s²；轴振动加速度峰值为0.15m/s²，与有限元模型的计算结果相近。由于有限元模型中对变压器样机底部加有固定约束，而实验测试时，样机体积较小其底部直接放于地面，难以达到理想的固定约束要求，因此实验测试值与有限元仿真计算结果波形会存在一定差异。实验测量与有限元计算结果的振动周期同为0.01s，因此可验证有限元模型的正确性，其可以用于非晶合金变压器空间样本点的计算。

图6 振动加速度实验测量结果

图7 振动加速度有限元计算结果

3 代理模型预测结果分析

3.1 代理模型预测结果

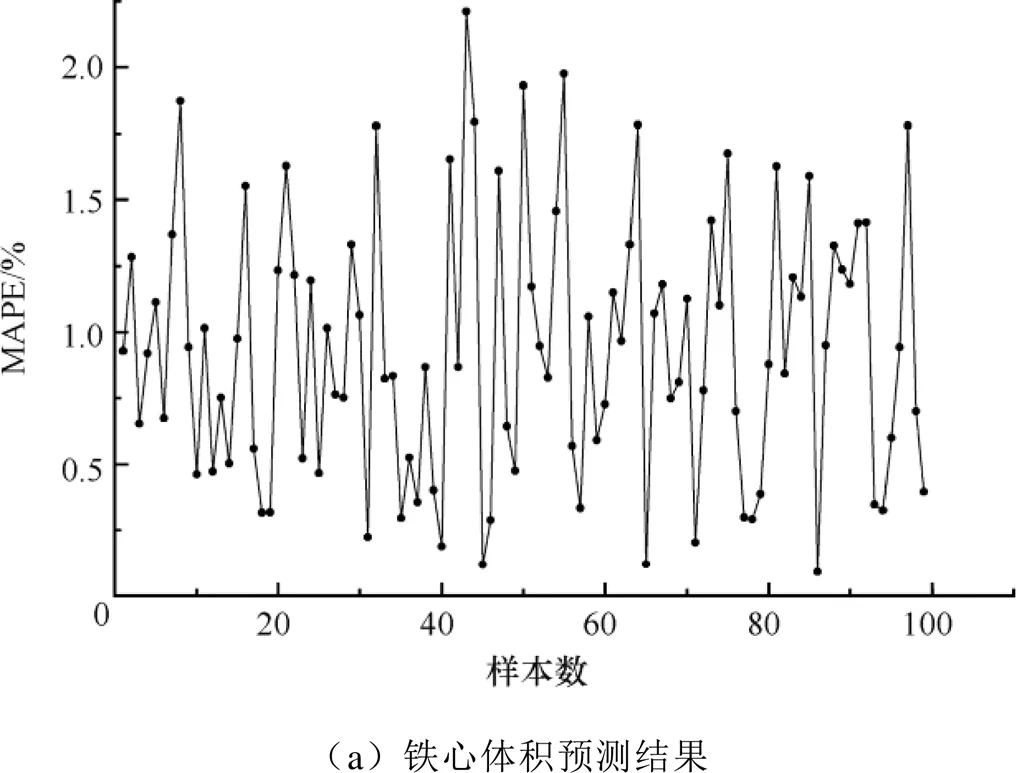
为验证所提出方法的合理性，在得到的最优Attention-LSTM模型的预测结果中随机选取100组测试集预测结果与有限元计算结果进行对比，铁心体积和振动加速度的相对百分误差（MAPE）如图8所示。铁心体积的预测结果MAPE普遍在2.5%以下，振动加速度的MAPE大多在5%以下。可以证明本文提出的Attention-LSTM预测模型具有优异的预测效果，能够准确地表达出非晶合金变压器的5个结构参数与振动、体积之间的非线性关系，从而避免了复杂的电磁分析计算。

3.2 代理模型效果对比分析

主成分分析（principal component analysis, PCA）法常用于传统代理模型处理复杂数据问题前的数据预处理。因此，采用传统代理模型BP神经网络、径向基函数（radial basis function, RBF）、支持向量机（support vector machine, SVM）对使用PCA方法降维后的数据进行训练和预测。使用PCA方法对传统代理模型的影响如图9所示。使用PCA方法对原有数据降维后，几种代理模型的预测精度均有提升。使用PCA方法可以有效提升传统代理模型处理复杂数据的能力。

图9 PCA对传统代理模型的影响

不同于传统代理模型，Attention-LSTM模型具有多层神经网络自动提取深层次特征的能力。因此，Attention-LSTM模型在处理复杂数据问题时并不需要使用PCA方法进行预处理。PCA对LSTM模型的影响如图10所示。PCA方法对于Attention-LSTM模型的预测效果并没有明显的提升。证明Attention- LSTM模型在处理复杂数据问题时，并不依赖PCA方法，因而降低了模型的复杂程度。

图10 PCA对LSTM代理模型的影响

为验证Attention-LSTM模型的有效性，将Attention-LSTM模型与传统代理模型的预测结果进行对比，不同代理模型的预测精度对比见表3。

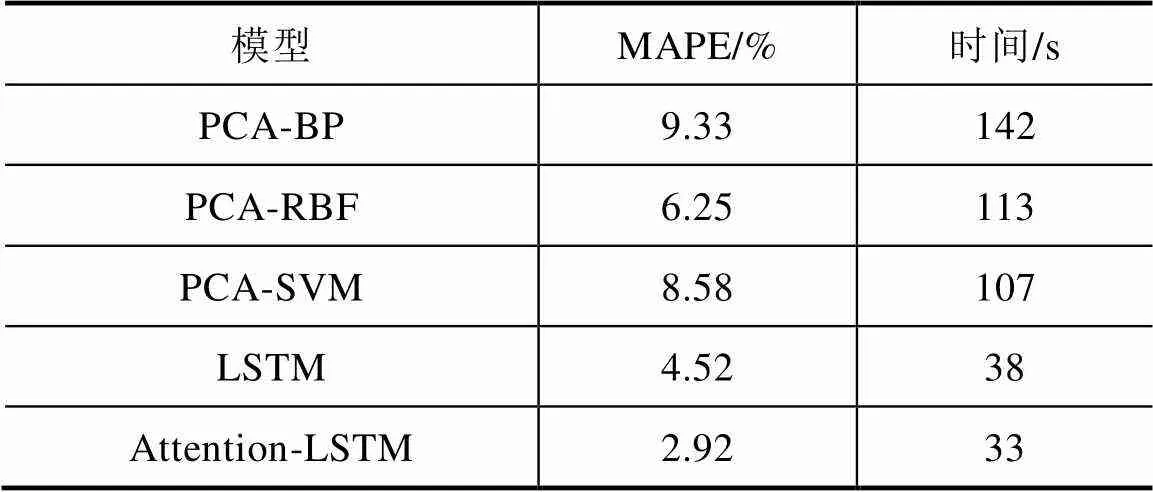
表3 不同代理模型对比

将复杂数据经过PCA预处理后的BP神经网络、径向基函数和支持向量机方法与Attention-LSTM算法对200组测试数据集的预测精度数据进行对比，结果见表3。可以看出，Attention-LSTM模型的预测精度最高，并且相较于其他经过PCA处理的代理模型，LSTM模型在引入Attention机制后，增强了数据的预测精度。使用有限元仿真计算模型计算变压器样机的时间约为12min（720s），而Attention- LSTM模型的运算时间仅为33s，约为有限元模型计算时间的1/20，极大减少了样机的计算时间，提高了该类工程问题的计算效率。

4 结论

本文基于Attention-LSTM建立了用于非晶合金变压器性能参数预测的代理模型。根据变压器结构与实际应用中需要解决的问题，建立典型的变压器样本数据，通过合理的分析策略完成了模型参数的确定及案例验证。实验结果证明，Attention-LSTM作为变压器代理模型具有很好的预测精度，可以准确地表达变压器结构参数与振动之间的非线性关系，并与有限元分析方法可以相互验证。这为处理变压器优化设计中的复杂数据问题提供了一种新的代理模型建立方法。

[1] 王辉. 变压器磁场分析法与解析法的应用对比[J]. 变压器, 2000, 37(8): 22-26.

[2] 李冰, 王泽忠, 刘恪, 等. 特高压变压器直流偏磁对绕组电流的影响[J]. 电工技术学报, 2020, 35(7): 1422-1431.

[3] 陈伟根, 滕黎, 刘军, 等. 基于遗传优化支持向量机的变压器绕组热点温度预测模型[J]. 电工技术学报, 2014, 29(1): 44-51.

[4] DANESHMAND S V, HEYDARI H. A diversified multiobjective simulated annealing and genetic algo- rithm for optimizing a three-phase HTS transformer[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(2): 1-10.

[5] 潘再平, 张震, 潘晓弘. 基于QPSO算法的电力变压器优化设计[J]. 电工技术学报, 2013, 28(11): 42-47.

[6] TRIA L R, ZHANG D, FLETCHER J. High-frequency planar transformer parameter estimation using differ- ential evolution[C]//2015 IEEE International Magnetics Conference (INTERMAG), Beijing, 2015.

[7] FORRESTER A I J, KEANE A J. Recent advances in surrogate-based optimization[J]. Progress in Aerospace Sciences, 2009, 45(1): 50-79.

[8] 张剑. 基于代理模型技术的高速列车性能参数设计及优化[D]. 成都: 西南交通大学, 2015.

[9] XIA Bin, REN Ziyan, KOH C S. Utilizing kriging surrogate models for multi-objective robust optimi- zation of electromagnetic devices[J]. IEEE Transa- ctions on Magnetics, 2014, 50(2): 693-696.

[10] 陈亚, 李萍. 基于神经网络的短期电力负荷预测仿真研究[J]. 电气技术, 2017, 18(1): 26-29.

[11] 杨杰, 黄晨, 石恒. 径向基函数神经网络补偿的悬浮球悬浮高度自适应滑模控制[J]. 电气技术, 2020, 21(2): 26-30.

[12] 彭珍瑞, 郑捷, 白钰, 等. 一种基于改进MCMC算法的模型修正方法[J]. 振动与冲击, 2020, 39(4): 236- 245.

[13] ACAR E, RAIS-ROHANI M. Ensemble of meta- models with optimized weight factors[J]. Structural and Multidisciplinary Optimization, 2009, 37(3): 279- 294.

[14] SHAO Zhenfeng, ZHANG Linjing, WANG Lei. Stacked sparse autoencoder modeling using the synergy of airborne LiDAR and satellite optical and SAR data to map forest above-ground biomass[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(12): 5569-5582.

[15] QIU Gao, LIU Youbo, LIU Junyong, et al. Analytic deep learning-based surrogate model for operational planning with dynamic TTC constraints[J]. IEEE Transactions on Power Systems, 2020: 1-8.

[16] BARMADA S, FONTANA N, SANI L, et al. Deep learning and reduced models for fast optimization in electromagnetics[J]. IEEE Transactions on Magnetics, 2020, 56(3): 1-4.

Transformer surrogate model based on attention and long-short term memory

JIN Liang1,2FENG Yulin1CAO Jiahao1WANG Yanyang1

(1. Tianjin Key Laboratory of Advanced Technology of Electrical Engineering and Energy, Tiangong University, Tianjin 300387; 2. State Key Laboratory of Reliability and Intelligence of Electrical Equipment, Hebei University of Technology, Tianjin 300130)

The design parameters and performance data of power transformers are often very complex considering many factors such as energy exchange efficiency, noise, volume and weight. Therefore, how to establish transformer surrogate model is an urgent problem to be solved. The surrogate-based optimization (SBO) can effectively solve the problem of long optimization time. In this paper, the surrogate model of transformer design parameters and performance data is established by deep learning to achieve high precision prediction of transformer performance optimization objectives and effectively reduce the time required for transformer performance analysis and optimization. Firstly, based on the deep learning model of long-short term memory network (LSTM), the nonlinear mapping between various parameters of amorphous alloy transformer is established, and the attention mechanism is added to enhance the prediction effect of the model. Finally, the proposed deep learning surrogate model is verified by finite element simulation experiment and compared with other commonly used surrogate models. The results show that the attention and long-short term memory surrogate model is superior in prediction accuracy.

amorphous alloy transformer; finite element method; surrogate model; deep learning; long-short term memory (LSTM); attention

国家自然科学基金面上项目（51977148）

2020-12-12

2020-12-29

金 亮（1982—），男，博士，副教授，主要研究方向为工程电磁场与磁技术、电磁场云计算和电磁无损检测等。