一种基于改进网格搜索和广义回归神经网络的锂离子电池健康状态估计方法
2021-07-28陈志聪吴丽君程树英林培杰
姚 远 陈志聪 吴丽君 程树英 林培杰
一种基于改进网格搜索和广义回归神经网络的锂离子电池健康状态估计方法
姚 远 陈志聪 吴丽君 程树英 林培杰
(福州大学物理与信息工程学院,福州 350108)
为了准确估计锂离子电池的健康状态,本文提出一种新的基于改进网格搜索(GS)和广义回归神经网络(GRNN)的估计方法。首先,对集中的数据进行处理,并通过相关性分析方法,提取有效的特征数据,包括电压、电流等。其次,提出一种基于改进网格搜索和广义回归神经网络的回归模型来估计电池的健康状态。最后,使用两个锂离子电池公共数据集验证提出的估计方法。实验结果证明,与其他估计方法相比,所提方法在准确性、泛化性和可靠性方面具有优势。
锂离子电池;健康状态;特征提取;广义回归神经网络(GRNN);混合算法
0 引言
随着全球对化石能源危机、环境污染和气候变化的关注度日益提高,新能源汽车,尤其是电动汽车(electric vehicle, EV)逐渐成为汽车工业的主流发展趋势[1]。由于能量密度高、寿命长和可靠性高的优势,锂离子电池(lithium-ion battery, LIB)已被广泛用作EV的储能设备。LIB的广泛使用致使自燃和爆炸等安全事故出现,严重损害了人身财产安全。为了安全地使用LIB为EV供电,必须实时监控其运行状态,以确保其安全性和可靠性。LIB是一个复杂的电化学系统,其失效模式受环境温度、放电深度、充放电机理等多种因素的影响,无法直接使用设备仪器进行测量。因此,准确估计电池健康状态(state of health, SOH)是当前电动汽车动力电池的应用和安全性研究的重点和难点[2-4]。
经过不断的探索,国内外对SOH估计方法的研究取得了一定的成果,目前主要有基于模型和基于数据驱动两种估计方法[5-7]。基于模型的方法主要是建立电模型或电化学模型将测量的电池信号(电压、电流和温度)与SOH连接起来[8]。文献[9]提出了一种布朗运动和粒子滤波算法结合的方法用于SOH估计,这使得SOH的准确短期预测成为可能。基于模型的方法具有良好的鲁棒性,可用于具有不同化学性质的电池SOH估计,但是需要深入了解电池的电化学机理。与基于模型的方法相比,数据驱动方法不需要研究电池内部的化学机理,仅根据电池退化信息估计SOH的黑盒模型[10]。文献[11]利用数据处理的分组方法(group method of data handling, GMDH)建立了微分几何特性和SOH之间的关系来估计电池当前状态;该方法避免了很多训练数据,但是估计精度不够高。文献[12]采用先验知识为基础的神经网络和马尔可夫链的方法来估计SOH,尽管估计精度逐渐提高,但是此方法从LIB的所有退化过程中随机选择大量数据来训练模型,增加了模型的复杂度。
针对上述存在的问题,本文提出一种新的SOH估计方法。首先,通过对数据集进行数据处理,并采用相关性分析的方法选择提取相关性较高的特征信息,大大减少训练数据,然后建立基于改进网格搜索(grid search, GS)和广义回归神经网络(generalized regression neural network, GRNN)的模型进行SOH估计。与其他方法相比,该方法可大大缩短训练时间,具有更强的泛化能力和更准确的SOH估计结果。
1 数据处理和特征提取
本文主要采用两个公共锂离子电池数据集。其中一个来自美国国家航空航天局(national aeronautics and space administration, NASA)卓越预测中心[12],数据集是通过对几种类型的电池(包括商用可充电锂离子电池18650)进行循环充放电获得的。以B0005为例,电池额定容量约为1.8A∙h,充电时先进行1.5A恒流充电,直到电压达到4.2V,然后进行4.2V恒压充电,直到电流降至20mA;放电时以2A恒流放电,直到电压降至2.7V。另一个数据集来自美国马里兰大学高级生命周期工程研究中心(center for advanced life cycle engineering, CALCE)[13],该数据集同样采用先恒流后恒压的充电方法,但是选择的电流不同。以CS2—35为例,电池的额定容量约为1.1A∙h,充电时先进行0.55A恒流充电,直到电压达到4.2V,然后进行4.2V恒压充电,直到电流降至50mA;放电时以1.1A恒流放电,直到电压降至2.7V。通常,SOH代表电池容量减少和内部电阻增加的百分比。本文选择容量比作为SOH的定义[14],其表达式为

式中:C为第次充放电循环的电池容量;0为电池的初始容量。
由于两个公共数据集中电池类型太多,因此本文从两个数据集中各选取一个具有代表性的电池型号数据集,即B0005和CS2—35数据集,通过对数据进行预处理,经过数据清洗和数据规范等方法,剔除记录异常的数据,最终得到的电池SOH变化曲线如图1所示。
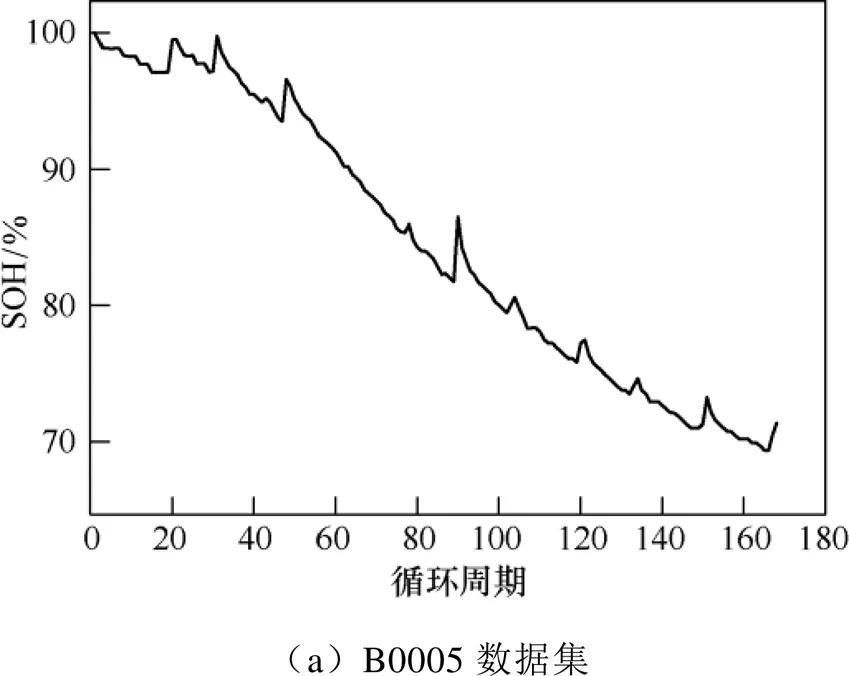
电池的容量退化主要受其工作电压、电流和温度等因素的影响,其容量退化程度也反映在这几个特性变化引起的数据变化中。基于选用的两个公共数据集的充放电模式,本文从数据集中提取平均充电电压、恒流充电时间、平均放电电压、平均放电温度等特征,通过采用相关系数的相关性分析法对选取特征与SOH的相关性进行分析,选取相关性较高的几个特征作为模型输入。相关系数法采用的是皮尔逊相关系数[15],其表达式为

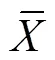
表1为提取的特征与SOH 的相关性分析结果。对经过数据处理提取的特征参数进行分析,从表1可以看出,平均充电电压和SOH呈负相关,平均放电电压与SOH呈正相关,因此总的平均电压和SOH几乎无关联;平均放电温度与SOH的相关性较高,但是由于CS2—35数据集中未统计电池的放电温度变化,而电池的充电都是在室温条件下进行的,因此不选择此类特征;由于充电过程都是先恒流后恒压,无法直接选择电流变化来分析,因此选择充电时间代表电流变化对SOH的影响,从表1中可以看出,总的充电时间与SOH的相关性较高,因此选择总的充电时间作为输入特征。综上所述,本文选择平均充电电压、充电总时间、平均放电电压三个特征作为建立SOH估计模型的输入参数。
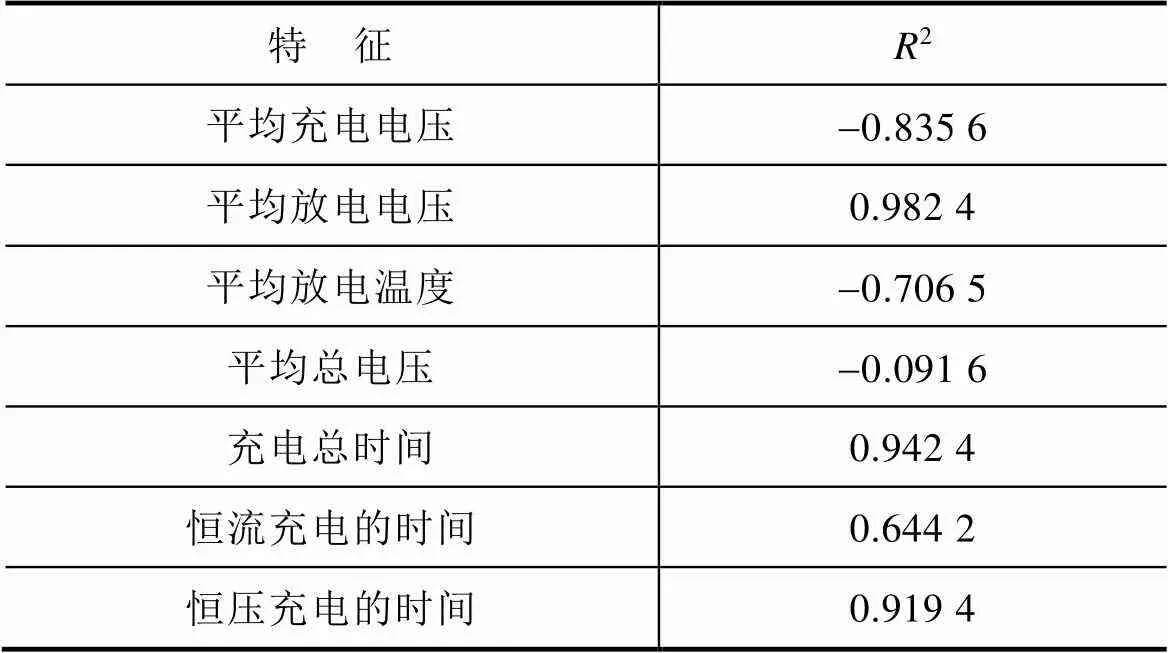
表1 提取特征与SOH的相关性分析结果
2 基于改进GS-GRNN的SOH估计方法
2.1 GRNN回归模型
GRNN是美国学者在20世纪90年代提出的,它是径向基函数神经网络(radial basis function neural network, RBF)的特例[16]。GRNN具有较强的非线性映射能力和灵活的网络架构,还具有较高的鲁棒性和容错能力,这些优点使其非常适合处理非线性问题。此外,GRNN在较小样本数据中的网络收敛能力和学习速度更有优势。锂离子电池SOH的变化是由多种复杂因素叠加引起的,而且本文的样本数据较小。综上所述,GRNN适用于估计SOH这种没有明确定量公式描述的物理量。
GRNN的模型结构如图2所示。从图2可以看出,GRNN是由作用完全不同的四层组成:输入层无需对数据进行处理,神经元个数与输入特征维数相同,作用是将输入传递到下一层;模式层对输入的数据进行非线性变换,模式层的神经元个数比输入层多,与样本数目相关,其激活函数通常采用高斯函数;求和层主要计算由神经元输出加权的总和及神经元输出的总和;输出层的神经元个数与模型输出的维数相同,每个神经元的输出值为对应的求和层输出值与求和层第一个神经元输出值相除。

图2 GRNN模型结构
GRNN的高斯激活函数表达式为[17]

式中:为输入变量;X为模式层中的第个神经元;为训练样本个数;为平滑参数。是GRNN惟一一个超参数,如果平滑参数的值设置不当,可能导致模型的估计结果不够准确,因此需要采用参数优化算法进行参数寻优。
2.2 改进GS方法
GRNN模型仅有平滑参数一个参数需要进行寻优,如果选择复杂的参数优化算法可能会导致整体算法的复杂度增加,本文选用的数据集样本特征数量只有几百,综合考虑,最后选择采用GS方法来进行参数寻优。
GS是一种穷举搜索的方法,其基本思想是搜索所有可能的参数设置。在本文中,模型的评价指标选取的是方均误差(mean square error, MSE),GS实际应用是在所有的平滑参数的可能值中,通过循环遍历,尽可能尝试每种可能性,找到能使MSE最小的平滑参数值。GS的步长取值会影响网格的尺寸,当网格尺寸很小时,将耗费很多的计算资源,使得搜索更加困难。
针对上述问题,本文提出一种改进GS方法。先采用大步长对参数进行初步寻优,以此减小寻优范围,在得到较小MSE的参数区间内进行小步长寻优,最终找到最优参数。改进GS方法能够减少多余的计算,提高整体算法的效率,节省时间。
2.3 混合算法
本文整体实验流程如图3所示。首先对两个数据集进行数据处理,通过数据清洗和数据规范等方法提取电池充放电过程的特征,采用相关性分析的方法,选择了三个与SOH相关性最高的特征作为算法模型的输入,然后搭建基于改进GS-GRNN的回归算法模型,通过改进的GS方法对GRNN模型的参数进行寻优,并训练得到最优模型,最后在测试集上对模型进行效果评估,并与其他SOH估计方法进行对比。

图3 整体实验流程
3 实验结果与分析
本文选择在两个公共数据集上验证搭建的算法模型的可行性。两个数据集来源于NASA和CALCE,是通过在实验室中进行电池循环充放电并记录特征数据变化得到的,数据来源可靠。数据处理和特征选择部分在Matlab2018a上进行;算法模型搭建部分在Python3.7上进行。通过在搭建的算法模型上进行训练估计,得到B0005数据集的SOH估计结果和估计误差结果分别如图4和图5所示。
从图4中的SOH真实值变化可以看出,SOH并不是一味地下降,由于锂电池内部的复杂化学反应,在SOH降低期间,会发生局部再生和波动,导致SOH的起伏变化,从而增加了估计难度。SOH的波动变化在一定程度上会反映在电压、电流等特征变化上,因此本文在数据处理阶段选择了与SOH变化相关性较高的几个特征,当SOH出现波动时,本文选择的对应特征也会在一定范围内随之变化,能够为GRNN模型提供较好的训练数据,再加上GRNN的优势,训练得到的模型能够更加准确地估计SOH。从图5的误差结果中可以看出,模型的估计误差基本在0.04%内,但个别值的估计误差较大,这是由于锂离子电池SOH变化过程中,某些电压、电流特征的变化幅度很小,输入数据太相近导致在后面的估计中不能完全准确地估计SOH。
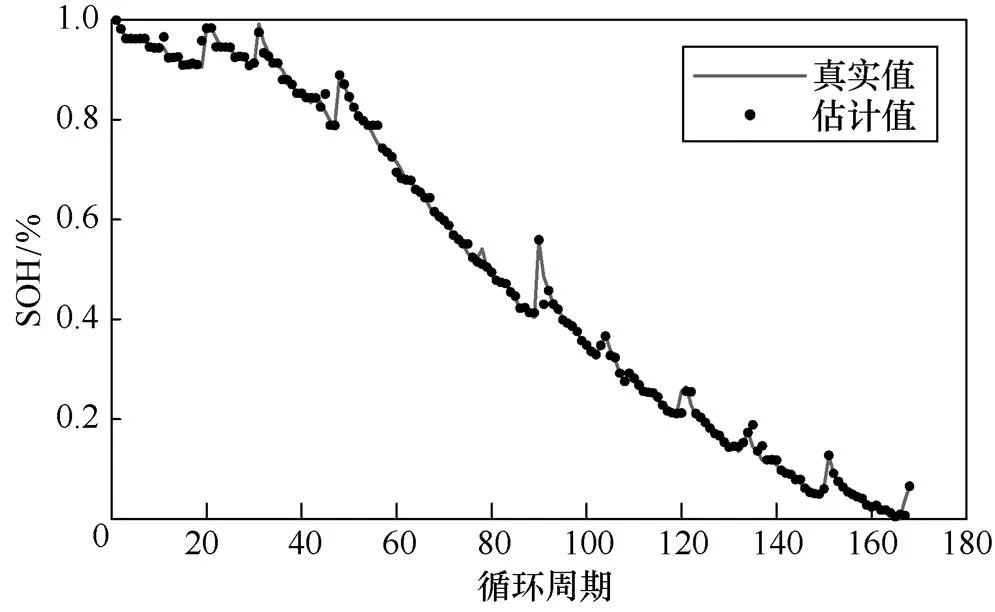
图4 B0005数据集SOH估计结果与真实值对比

图5 B0005数据集SOH估计误差结果
CS2—35数据集的SOH估计结果和估计误差结果分别如图6和图7所示。从图6的估计结果对比可以看出,相比较在B0005上的估计结果,在CS2—35数据集上的估计结果更加准确。原因有两个方面:①该数据集的循环周期约为800,训练样本的增加在一定程度上能够让模型更好地学习SOH的变化,从而更好地拟合SOH的变化;②对比B0005数据集,该电池SOH的变化波动较小,通过样本的训练学习,小幅度的波动变化能够被模型准确估计得到。从图7可以看出,模型的估计误差基本在0.02%内,误差较小,证明模型能够较为准确地估计电池SOH。

图6 CS2—35数据集SOH估计结果与真实值对比

图7 CS2—35数据集SOH估计误差结果
本文选择MSE和平均绝对误差(mean absolute error, MAE)作为算法模型的评价指标,表2为多种算法的性能对比,包括本文方法改进GS-GRNN、GRNN、粒子群算法(PSO)-支持向量机(SVM)、PSO-BP神经网络(BPNN)、K最邻近算法(KNN)和高斯过程回归算法(GPR)。本文方法针对B0005数据集的MSE和MAE分别约为0.013%和0.5%,针对CS2—35数据集的MSE和MAE分别约为0.005%和0.4%。从表2可以看出,与GRNN和其他算法相比,本文算法的SOH估计精度较高。实验结果表明,本文提出的改进GS-GRNN回归模型能够较为准确地实现SOH估计。

表2 多种算法性能对比
4 结论
本文的重点是提出和验证了基于改进的网格搜索和广义回归神经网络模型的SOH估计方法。首先,对两个数据集进行数据预处理,通过数据清洗和数据规范对数据进行优化,并对提取的数据特征进行相关分析,从充电和放电曲线中选择与SOH高度相关的三个特征(平均充电电压、充电总时间、平均放电电压)作为回归模型输入。然后,搭建了基于改进GS-GRNN回归模型,通过参数寻优算法得到最优的算法模型,最终得到SOH估计结果。在实验结果中,本文方法在两个数据集上的MAE分别约为0.5%和0.4%,与其他SOH估计方法相比,该方法具有较高的精度和稳定性。通过对不同的电池数据集进行评估,证明了本文方法强大的泛化能力和通用性。综上所述,本文提出的方法可以准确估算电池的SOH,非常适合用于电池管理系统中的电池监测管理。
[1] 杨若岑, 冬雷, 廖晓钟, 等. 电池剩余容量估算方法综述[J]. 电气技术, 2019, 20(10): 1-5, 57.
[2] 李建林, 马会萌, 惠东. 储能技术融合分布式可再生能源的现状及发展趋势[J]. 电工技术学报, 2016, 31(14): 1-10, 20.
[3] 孙冬, 许爽. 梯次利用锂电池健康状态预测[J]. 电工技术学报, 2018, 33(9): 2121-2129.
[4] 颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 电工技术学报, 2019, 34(18): 3937-3948.
[5] WEI Jingwen, DONG Guangzhong, CHEN Zonghai. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5634-5643.
[6] GUO Peiyao, CHENG Ze, YANG Lei. A data-driven remaining capacity estimation approach for lithium-ion batteries based on charging health feature extraction[J]. Journal of Power Sources, 2019, 412: 442-450.
[7] 吕航, 刘承志, 尹栋, 等. 深海动力磷酸铁锂电池组均衡方案设计优化[J]. 电工技术学报, 2016, 31(19): 232-238.
[8] 郭永芳, 黄凯, 李志刚. 基于短时搁置端电压压降的快速锂离子电池健康状态预测[J]. 电工技术学报, 2019, 34(19): 3968-3978.
[9] DONG Guangzhong, CHEN Zonghai, WEI Jingwen, et al. Battery health prognosis using brownian motion modeling and particle filtering[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 8646-8655.
[10] QU Jiantao, LIU Feng, MA Yuxiang, et al. A neural- network based method for RUL prediction and SOH monitoring of lithium-ion battery[J]. IEEE Access, 2019, 7: 87178-87191.
[11] WU Ji, WANG Yujie, ZHANG Xu, et al. A novel state of health estimation method of Li-ion battery using group method of data handling[J]. Journal of Power Sources, 2016, 327: 457-464.
[12] DAI Houde, ZHAO Guangcai, LIN Mingqiang, et al. A novel estimation method for the state of health of lithium-ion battery using prior knowledge-based neural network and Markov chain[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7706-7716.
[13] TIAN Jinpeng, XIONG Rui, YU Quanqing. Fractional- model-based incremental capacity analysis for degrad- ation state recognition of lithium-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1576-1584.
[14] WANG F K, MAMO T. A hybrid model based on support vector regression and differential evolution for remaining useful lifetime prediction of lithium-ion batteries[J]. Journal of Power Sources, 2018, 401: 49-54.
[15] XIONG Rui, LI Linlin, TIAN Jinpeng. Towards a smarter battery management system: a critical review on battery state of health monitoring methods[J]. Journal of Power Sources, 2018, 405: 18-29.
[16] 彭周宁, 林培杰, 赖云锋, 等. 基于混合灰色关联分析-广义回归神经网络的光伏电站短期功率预测[J]. 电气技术, 2019, 20(10): 11-18.
[17] YANG Duo, ZHANG Xu, PAN Rui, et al. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve[J]. Journal of Power Sources, 2018, 384: 387- 395.
A health state estimation method for lithium-ion battery based on improved grid rearch and generalized regression neural network
YAO Yuan CHEN Zhicong WU Lijun CHENG Shuying LIN Peijie
(College of Physics and Information Engineering, Fuzhou University, Fuzhou 350108)
In order to accurately estimate the state of health (SOH) of lithium-ion batteries, this paper proposes a new estimation method based on improved grid search (GS) and generalized regression neural network (GRNN). Firstly, data processing is performed on the data set, and effective characteristic data including voltage and current are extracted through correlation analysis method. Secondly, a regression model based on improved grid search and generalized regression neural network is proposed to estimate the health of the battery. Finally, two public data sets of lithium-ion batteries are used to verify the proposed estimation method. Experimental results prove that this method has the advantages of accuracy, generalization performance and reliability compared with other estimation methods.
lithium-ion battery; state of health (SOH); feature extraction; generalized regression neural network (GRNN); hybrid algorithm
2020-11-26
2020-12-23
姚 远(1997—),男,湖北省襄阳市人,硕士研究生,主要从事锂离子电池健康状态估计和剩余使用寿命预测工作。
