地铁车站同时在站人数模型研究

王洪锐 车轮飞 康恒 刘俊* 徐新华

1 武汉地铁集团运营有限公司

2 中铁第四勘察设计院集团有限公司

3 华中科技大学建筑环境与能源应用工程系

0 引言

随着中国经济的快速发展和城市化进程的推进，城市轨道交通也在快速发展。地铁的通风空调系统设计是地铁设计中十分重要的一部分，通风空调设计的好坏直接影响整个地铁车站的运行能耗、舒适度、安全性[1-3]。为了更好地进行设计和选型，需要对地铁车站的逐时负荷进行计算[4]。与此同时，地铁空调系统的预测控制也需要车站的负荷预测。人员负荷是地铁负荷的重要组成部分。在负荷计算中，人员负荷根据人员密度进行计算，而关于人员密度的计算，目前主要采用逐时客流密度系数计算人员密度和采用固定的上行与下行停留时间计算人员密度。逐时客流密度系数法以远期高峰客流乘逐时客流密度系数得到车站的逐时客流量。远期高峰客流量利用原有预测数据或预测的客流量，结合土地规划和交通规划前提进行推算，逐时客流密度系数是取值在0 到1 之间，反映逐时客流相比于远期高峰客流之间关系的常数[5-6]。另一种常用方法为采用统一且固定的上行与下行停留时间（如上行5 分钟下行3 分钟）计算人员密度[7]。这两种计算方法计算难度大，难以针对各个站点的实际情况准确地计算出其人员密度。

本文提出地铁车站同时在站人数计算模型，并通过简易的实地测量实验辨识模型中的参数。该模型利用实时统计的客流量及模型参数（即进出站旅客停留时间）简单高效地计算出地铁车站同时在站人数。该计算模型及其参数辨识方法避免了传统方法如遥感测量造价高难度大或采用统一的上下行停留时间计算不够准确等缺点，能够简单，高效和实时地计算地铁车站同时在站人数。该同时在站人数可用于地铁车站公共区人员负荷预测，为地铁车站通风空调的负荷计算及空调系统预测提供参考。

1 地铁车站同时在站人数模型

地铁车站公共区的负荷，主要由以下几个部分组成：人员负荷，照明负荷，设备负荷，围护结构负荷，新风负荷和其他负荷。地铁车站属于地下建筑，其围护结构负荷较为稳定[8]，对空调系统的控制影响较小。照明负荷与设备负荷与地铁车站的照明与设备使用情况相关，其规律较易掌握。新风负荷可以通过实时监测室外气象参数进行预测。地铁车站公共区间人员负荷与人流密度相关，对于某一典型的地铁车站，其面积一定，因此人员负荷与此时所容纳的人数，即同时在站人数相关。除去少量的地铁工作人员外，地铁车站公共区人员主要由旅客组成。旅客在地铁车站主要有四种行为，即进站、出站、上车和下车。旅客在地铁车站内的行为示意图如图1 所示。其中，实心圆点表示进站上车的旅客，空心方点表示下车出站的旅客。

图1 地铁车站旅客行为示意图

地铁车站在运行过程中，人流量变化较大，同时人处于不断移动的状态中，同时在站人数是一个动态值，难以测量[9]。地铁车站内的旅客可分为两种，即进站上车的旅客和下车出站的旅客，分别称为进站旅客和出站旅客。进站旅客从室外进入地铁车站公共区到上车离开地铁车站公共区所停留的时间称为进站停留时间。同样的，把出站旅客从下车进入地铁车站公共区到离开地铁车站公共区所停留的时间称为出站停留时间[10]。

根据人数守恒可知，由进出站旅客客流量和旅客停留时间可计算得到地铁车站公共区间所停留的人数。很显然，由于进站安检和候车等因素的影响，旅客进站上车和下车出站所停留的时间并不相同。因此，同时在站上车旅客人数和同时在站下车旅客人数应分别计算，两者之和为地铁车站同时在站人数。地铁车站同时在站人数计算模型如式（1）所示。

式中：Q 为同时在站人数，人；X 为进站旅客客流量，人/小时；Y 为出站旅客客流量，人/小时；A 与B 为参数，则分别为进站旅客停留的时间及出站旅客停留时间，小时。

从式（1）可以看出，要想计算得到同时在站人数，需知道X 和Y 两个变量及A 和B 两个参数。对于地铁车站来说，进站旅客客流量X 和出站旅客客流量Y可以通过车站进出口闸机统计数据获得。对于进站旅客停留时间A 和出站旅客停留时间B 这两个参数，可通过参数辨识获取。本文提出一种基于实际测量的参数辨识方法，辨识得到以上两个参数，进而根据模型计算地铁车站同时在站人数。

2 模型参数辨识

同时在站人数与进站客流量，出站客流量，进站旅客停留时间以及出站旅客停留时间有关。根据测量得到的同时在站人数和进站，出站客流量，可以辨识得到进站、出站旅客停留时间。为了辨识出更准确的进站、出站旅客停留时间，选取n 组同时在站人数和进站、出站客流量数据，进行参数辨识。根据同时在站人数模型式（1），可得该辨识过程的矩阵计算形式如式（2）：

式中：Qn为第n 小时内的实测同时在站人数；Xn为第n 小时内的进站旅客人数，Yn为第n 小时内的出站旅客人数。

最小二乘法是参数辨识过程中一种有效的计算方法，能得到实际测量值与计算值之间最小方差意义上的逼近，使这一组解的欧几里德范数达到最小。在进行参数辨识时，为了保证足够的辨识精度，所选取的数据组个数n 大于式（2）中矩阵[A B]T的元素个数2。式（2）的线性方程组没有一般意义上的解，需要解出其最佳逼近解，即最小二乘解[11]。

式（2）可以简写为式（3）。

式中：T=[Q1,Q2,…,Qn]T，为n 组实测同时在站人数组成的n 维列向量；为由n 组逐时进站、出站客流量数据所组成的客流矩阵；Z=[A,B]T，为进站、出站旅客停留时列向量。

对不相容的线性方程组(3)：PP+是Cn空间向R(P)上的一个正交投影变换所对应的矩阵，故有||P(P+T)-T||≤||PZ-T||，Z∈C2。即Z=P+T 是式（3）的最小二乘解[12]。其中，P+为矩P 的加号广义逆，R(P)为矩阵A 的列空间。式（2）中辨识的参数Z=[A B]T可由逐时进站、出站旅客人数组成的系数矩阵的加号广义逆P 乘测量得到的逐时同时在站人数组成的列向量T 得到。

旅客停留时间参数辨识过程如下：首先统计进站旅客客流量X 和出站旅客客流量Y；再实际测量得到相应时间的同时在站人数Q；最后根据地铁车站同时在站人数计算模型，采用最小二乘法辨识得到进站旅客停留时间A 和出站旅客停留时间B。

3 客流量统计与同时在站人数测量

3.1 客流量统计

地铁车站中央监控系统可以提供地铁各车站每日逐时进出站客流数据，但不能给出同时在站人数。以某地铁站为例，该车站的中央监控系统能给出的逐时客流数据的最小时间步长为一小时。某日旅客逐时进、出站人数分别如图2（a）和图2（b）所示。图2 描述了一天内逐时进站客流量和出站客流量的大小。8:00-9:00 段和18:00-19:00 段是两个高峰期，8:00-9:00内的进站和出站人数分别为2435 人和6274 人；18:00-19:00 内的进站和出站人数分别为5019 人和4536 人。

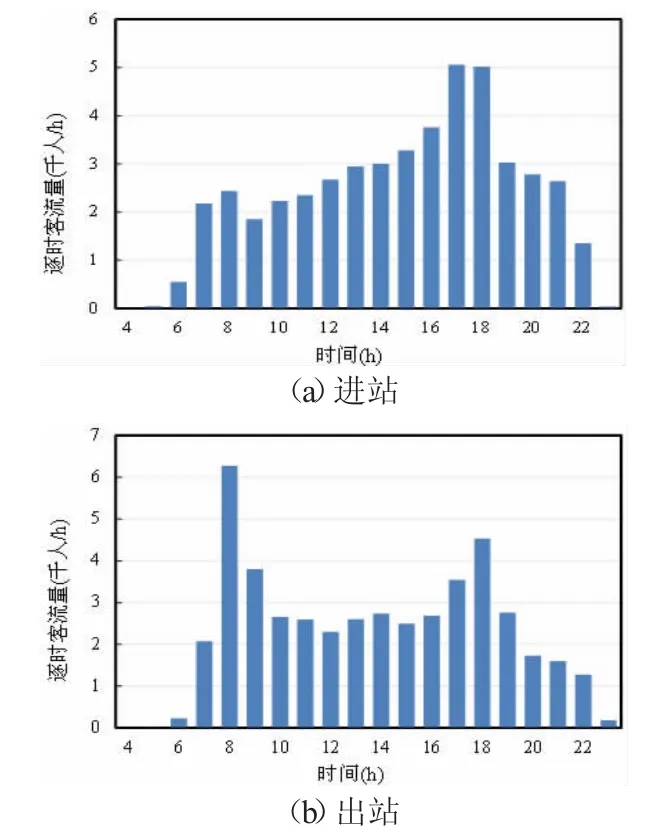
图2 逐时客流量图

3.2 同时在站人数测量

本文提出通过现场拍照的方式测量同时在站人数。站厅和站台同时在站人数拍照测量示意图分别如图3（a）和图3（b）。在图示位置，每十分钟间隔拍照取样一次，站厅站台同时拍照。根据拍照结果统计出同时在站人数并取平均，得到小时平均同时在站人数。某一时刻在站厅拍照取样的照片如图4。根据拍摄到的照片，统计拍摄区域在这一时刻的人数，可以得到这一时刻该区域的同时在站人数。

图3 地铁车站同时在站人数测量示意图

图4 同时在站人数实地测量照片

4 结果与分析

本文以武汉地铁某标准岛式车站为例，进行同时在站人数的实测与同时在站人数模型参数的辨识及模型的验证。选取某一天包含早高峰的测量数据进行参数辨识，数据包含从上午8 时至中午13 时，共五个小时内逐时进出站旅客数和测量得到的同时在站人数，如表1 所示。

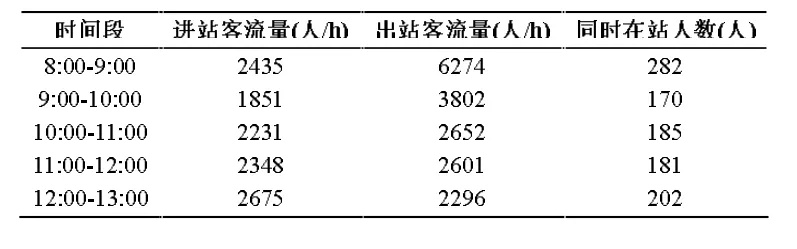
表1 武汉某地铁车站某日小时客流量

根据测量的旅客逐时进、出站人数和测量的同时在站人数，利用最小二乘法计算得出进站旅客停留时间A 为3.27 分钟；出站旅客停留时间B 为1.34 分钟。由进、出站旅客停留时间，计算车站同时在站人数。图5为测量当天车站同时在站人数的预测值与实测值的比较。预测值与实测值的最大相对误差出现在9:00-10:00 时间段。9:00-10:00 时间段内，同时在站人数的预测值为186，实测值为170，算得最大相对误差为9.4%；预测平均值与实测值平均值相同，都为204。

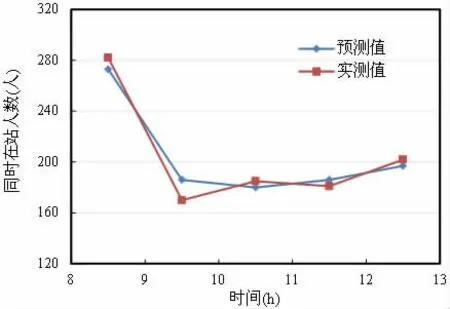
图5 模型预测值与实际测量值比较（参数辨识）

利用另一天的进出站人数和同时在站人数进行同时在站人数模型验证。模型的预测值和实测值如图6。预测值与实测值的最大相对误差出现在9:00-10:00时间段。9:00-10:00 时间段内，同时在站人数预测值为169，实测值为179，计算得出的最大相对误差为5.6%；同时在站人数的预测值平均为192，测量值平均为195，算得平均相对误差为1.5%。结果表明，地铁车站同时在站人数模型能较为准确地计算同时在站人数。

图6 模型预测值与实际测量值比较（模型验证）

本文进一步利用上述模型预测了该地铁车站某典型日全天的同时在站人数，如图7，可以看到在8:00-9:00 及18：00-19:00 时间段同时在站人数达到了高峰。

图7 全日同时在站人数变化图

5 结论

本文建立了地铁车站同时在站人数计算模型并采用最小二乘法进行参数辨识。进一步根据地铁车站逐时进、出站旅客人数和拍照统计得到的同时在站人数数据，辨识了进、出站旅客停留时间，并对结果进行验证。模型验证表明，预测值与实测值的最大相对误差出现在9:00-10:00 时间段，9:00-10:00 时间段内，同时在站人数预测值为169，实测值为179，计算得出的最大相对误差为5.6%；同时在站人数的预测值平均为192，测量值平均为195，算得平均相对误差为1.5%。结果进一步表明，该模型计算结果误差较小，具有很好的准确性和可靠性。针对不同的地铁车站，利用上述模型，计算该车站特性下的进、出站旅客停留时间，可以计算地铁车站的逐时同时在站人数，进一步可为地铁车站空调负荷预测及控制提供参考。