超低能耗建筑月能量平衡算法模型参数研究

张小波 瞿燕 李海峰

华东建筑设计研究院有限公司

在进行建筑能效评定时需要计算建筑的年采暖和空调能源需求，欧盟《建筑能效指令》中要求采用月能量平衡法来计算建筑的年采暖空调能源需求。EN ISO 13790-2008《建筑物的能耗特性——空间供暖和供冷能耗的计算》中对月能量平衡法进行了详细的介绍[1]。月能量平衡算法是一种准稳态算法，其计算建筑采暖空调需求的基本思路是计算建筑得热和建筑散热之间的平衡关系，采用得热利用系数和散热利用系数来计算建筑的采暖需求和空调需求。2017 年新发布标准EN ISO 52016-2017[2]替代了EN ISO 13790-2008，规定了计算建筑采暖空调能源需求，室内温度，显热和潜热负荷的计算方法。目前商用的建筑能效认证工具，如德国被动房研究所（PHI）开发的PHPP（Passive House Planning Package）、德国弗劳恩霍夫建筑物理研究所（FraunhoferIBP）和美国被动房研究所（PHIUS）合作开发的被动房认证软件WUFI Passive、英国公共建筑能效标识认证工具SBEM（Simplified Building Energy Model）、中国建筑科学研究院开发的近零能耗建筑评价工具IBE[3]、葡萄牙的早期可持续评估工具中的能源模块（ESSAT-EM）[4]等都是基于EN ISO 13790中给出的准稳态算法——月能量平衡算法。我国超低能耗建筑的国家标准也提出了“逐月计算”的准稳态算法来计算超低能耗建筑的采暖和空调能源需求。

1 月能量平衡算法的准确性与适用性

1.1 月能量平衡算法的准确性

根据EN ISO 13790 标准[1]，月能量平衡算法在计算得热利用系数和散热利用系数时，考虑了建筑热惯性及不同换热过程的影响；同时在计算公式中引入了两个模型常数，该标准给出的模型常数默认值分别为1.0 和15.0 h。2006 年，Corrado 和Fabrizio[5]针对意大利气候，通过与EnergyPlus 模拟结果进行对比，指出月能量平衡法用于单层和多层住宅建筑时，其模型常数最优值为6.3 和17.0 h；同时还提出一个计算散热利用系数的回归公式，在EN ISO 13790 计算公式的基础上引入了窗地比的影响。2007 年，Jokisalo 和Kurnitski[6]研究了月能量平衡算法在寒冷地区（芬兰）的适用性；研究发现，与动态能耗模拟软件IDA ICE 的模拟结果相比，月能量平衡算法计算得到的采暖需求会偏高46%或者偏低59%，这种偏高或偏低取决于建筑的类型及其热惰性；还指出这种准稳态算法应用于居住建筑还算合理，但是不适用于办公建筑。2008 年，Kokogiannakis 等人[7]利用EN ISO 13790 中的月能量平衡算法以及动态逐时算法软件ESP-r 和EnergyPlus来计算位于荷兰阿姆斯特丹和希腊雅典的建筑的年采暖空调能源需求，通过对比发现，不同算法计算得到的建筑年采暖空调能源需求结果差异显著，采用EN ISO 13790 给出的默认模型常数时，月能量平衡算法倾向于给出较差的建筑能效评级结果；在对月能量平衡算法进行优化后，得到的模型常数值分别为3.5 和10.0 h。2014 年，Santos 等人[4]以欧洲气候为例，研究了月能量平衡算法与EnergyPlus 在计算EN 15265 标准中的测试案例时结果上的差异，发现月能量平衡算法计算采暖需求的误差可达12%，空调需求的误差小于7%；进一步利用低层住宅对月能量平衡算法的两个模型常数以及导热，通风，太阳辐射和内热的计算公式进行修正。2018 年，余镇雨等人[3]对比了准稳态建筑负荷计算软件IBE 与动态模拟软件TRNSYS 对寒冷地区建筑负荷的计算结果，结果显示月能量平衡算法和动态模拟软件之间的负荷计算结果存在较大偏差，偏差可达20%。2019 年，Bruno 等人[8]针对地中海气候，研究月能量平衡算法与TRNSYS 之间的差异，发现利用EN 52016-1 中给定的月能量平衡算法及默认常数计算得到的空调能源需求与TRNSYS 之间的偏差为9.1%～61.2%；通过回归分析后，给出月能量平衡算法的模型常数分别为3.74 和26.2 h。

从现有的文献可以看出，采用标准给定的默认模型常数时，月能量平衡算法的计算结果与动态能耗模拟软件的计算结果之间存在显著的差异，因此有很多学者尝试针对月能量平衡算法的模型常数进行修正。

1.2 月能量平衡算法的适用性

尽管动态逐时建筑能耗模拟软件在建筑采暖空调负荷计算上比准稳态月能量平衡算法更加准确，但是逐时能耗模拟通常需要更多的输入参数和计算时间，而且在参数设置上也更为复杂，不利于建筑师和设计人员快速开展方案比选和优化工作。目前在进行建筑能效认证以及确定建筑能源需求指标时，准稳态算法依然在世界范围内被广泛使用。

已有的超低能耗建筑能效认证工具均采用EN ISO 52016-2017 标准中给定的默认值（1.0 和15.0 h）作为月能量平衡算法的模型常数值，未根据气候参数及建筑类型给出不同的常数值。Jokisalo 和Kurnitski[6]研究指出针对芬兰的气候，采用ISO 13790 标准给定的默认常数值来计算建筑的得热利用系数会高估建筑的采暖能源需求。考虑到中国地域广袤，不同气候区之间差异大，采用标准给定的默认常数值来计算得热利用系数和散热利用系数可能不能准确地考虑气候特点和建筑运行参数逐时逐日变化对建筑采暖空调能源需求的影响。因此本文研究月能量平衡算法中的模型常数的取值对其采暖空调能源需求计算结果的影响，来考察模型常数对该算法计算结果一致性的影响。第2 节对月能量平衡算法的基本公式进行简要介绍，并对该算法的模型常数对建筑采暖空调能源需求的影响进行敏感性分析；第3 节进一步对模型常数的影响机理进行分析；然后得出模型常数优化取值的必要性场合。

2 月能量平衡算法模型参数敏感性分析

2.1 月能量平衡算法基本公式

采用月能量平衡算法计算建筑的采暖和空调能源需求时的基本步骤如下：首先计算出采暖季或空调季建筑每月的得热量（QHG和QCG）和散热量(QHL和QCL)。然后，根据式（1）计算出得热散热比（γH和γC），再利用式（2）～（5）分别计算出采暖季的得热利用系数ηHG和空调季的散热利用系数ηCL。最后，通过式（6）和（7）分别计算建筑的采暖和空调能源需求。在计算得热或散热利用系数时需引入两个模型常数（a0和τ0），来计算建筑时间常数对建筑得热或散热利用系数的影响。EN ISO 13790 给出的常数默认值分别为1.0 和15.0 h。

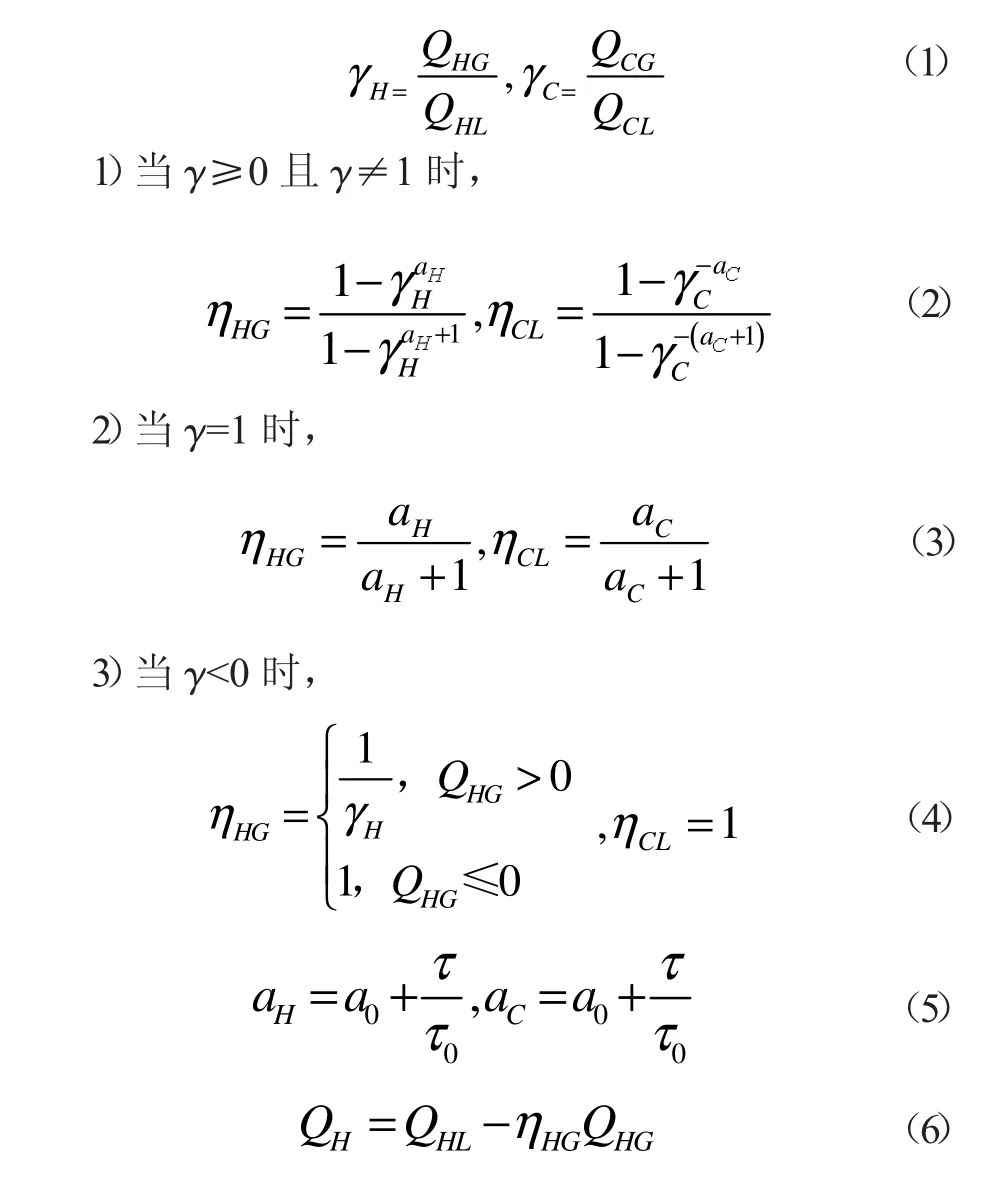
式中：QHG和QHL分别为采暖季建筑每月的得热量和散热量，kWh；QCG和QCL分别为空调季建筑每月的得热量和散热量，kWh；γH和γC分别为采暖季和空调季建筑每月的得热散热比，-；ηHG和ηCL分别为采暖季建筑每月的得热利用系数和空调季建筑每月的散热利用系数，-；aH和aL分别为月能量平衡算法在计算采暖季得热利用系数和空调季散热利用系数时的中间参数；QH为采暖能源需求，kWh；QC为空调能源需求，kWh；τ为建筑时间常数，h；a0、τ0分别为月能量平衡算法的模型常数；Ceff为建筑空间的有效热容，J/K；Htr为不包含地面的建筑围护结构传热系数，W/K；Hgr为地面的传热系数，W/K；Hve为通风相关的传热系数，W/K。

2.2 计算模型及工况设置

现有文献中给出的月能量平衡算法的模型参数如表1 所示。可以看出参数的取值存在较大的差异。为了研究模型参数对不同气候区建筑采暖空调能源需求计算结果的影响，本文采用PHPP 软件计算位于寒冷地区（北京）、夏热冬冷地区（上海）和夏热冬暖地区（广州）的办公建筑（建筑模型如图2 所示）的采暖空调能源需求，在计算过程中分别采用表1 中的数值作为月能量平衡算法的模型常数值。

表1 月能量平衡算法的模型常数取值

月能量平衡算法在计算建筑时间常数时考虑了建筑热惯性及不同换热过程的影响，如式（8）所示，但是导热项和通风项在计算采暖和空调能源需求时并不相同，因此该算法分别计算采暖季和空调季的建筑时间常数，具体算法可以参阅EN ISO 52016-1:2017标准[4]。由于建筑时间常数与建筑的热容及传热过程有关，在建筑各部分传热性能不变的前提下，可以通过改变建筑的热容来改变建筑时间常数。根据PHPP 软件，轻型围护结构建筑的热容为60 Wh/(m2·K)，重型围护结构建筑的热容为204 Wh/(m2·K)。为分析建筑热惯性对建筑采暖空调能源需求的影响程度，本文计算建筑时间常数分别为12 h，24 h，48 h，168 h 和240 h时的建筑采暖空调能源需求。

选取一办公建筑作为计算对象（如图2 所示），该办公建筑占地面积为3366.12 m2，总建筑面积为17200 m2，各朝向窗墙比及围护结构热工参数具体如表2 和表3 所示，建筑的气密性指标n50按0.6 h-1进行设计。

图2 某办公建筑效果图

表2 办公建筑各朝向窗墙比

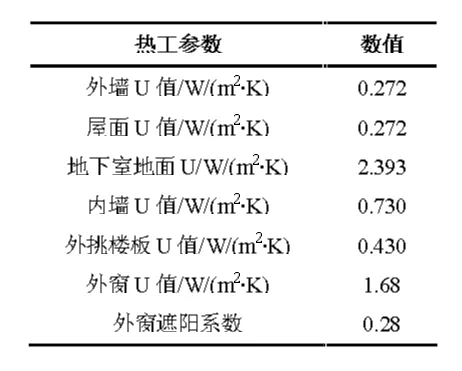
表3 办公建筑围护结构热工参数

2.3 采暖空调能源需求计算结果分析

三个气候区下，采用不同模型参数值时，PHPP 软件计算出的具有不同建筑时间常数的办公建筑的采暖空调能源需求分别如表4～6 所示。可以明显看出不同气候区下建筑的采暖空调能源需求符合气候特征，夏热冬冷地区以空调能源需求为主，寒冷地区以采暖能源需求为主，夏热冬暖地区的采暖能源需求可以忽略不计，而其空调能源需求明显高于夏热冬冷地区和寒冷地区。

表4 上海地区办公建筑采暖空调能源需求计算值/kWh/(m2·a)

表5 北京地区办公建筑空调能源需求计算值/kWh/(m2·a)

比较同一气候区、不同建筑时间常数下建筑的采暖空调能源需求可以分析建筑时间常数的影响，本文以建筑时间常数为12 h 和240 h 时的采暖空调能源需求之间的相对偏差来衡量建筑时间常数的影响程度。

a）采暖能源需求

对于广州地区，由于其采暖能源需求绝对值较小，可以忽略不计。PHPP 软件默认常数值和EN ISO 52016-2017 标准在计算上海地区办公建筑采暖能源需求时，建筑时间常数的影响可达30%以上。对于北京地区，其影响可达18%以上。采用Kokogiannakis 等人[9]和Bruno 等人[10]给出的模型常数值时，建筑时间常数对上海地区的影响可达10%，但是对北京地区的影响小于5%。采用Corrado 和Fabrizio[7]给出的模型常数值时，建筑时间常数对上海地区的影响为4.49%，而对于北京地区仅为1.64%。

b）空调能源需求

PHPP 软件默认常数值和EN ISO 52016-2017 标准在计算上海地区办公建筑空调能源需求时，建筑时间常数的影响超过10%。对于北京地区，其影响超过20%，而对于广州地区，其影响小于7%。采用Corrado和Fabrizio[7]，Kokogiannakis 等人[9]和Bruno 等人[10]给出的模型常数值时，建筑时间常数对三个气候区办公建筑空调能源需求的影响不超过3%。

从采暖空调能源需求计算结果来看，采用PHPP软件默认常数值和EN ISO 52016-2017 标准给出的模型常数值时，建筑时间常数对建筑采暖空调能源需求的影响较为显著，而采用表1 中的其他三组常数时，建筑时间常数对建筑采暖空调能源需求的影响较小。

3 月能量平衡算法模型参数影响机理分析

从月能量平衡算法的基本公式可知，该算法的模型常数以及建筑时间常数是通过建筑得热利用系数和散热利用系数来影响建筑的采暖能源需求和空调能源需求。建筑时间常数分别为12 h，24 h，168 h 和240 h 时，采用表1 中给出的模型常数值计算得到的得热或散热利用系数分别如图3 所示。得热或散热利用系数计算结果的差异主要是发生在得热散热比大于零的区段。

图3 月能量平衡算法模型常数取值对得热或散热利用系数的影响

PHPP 软件默认常数值和EN ISO 52016-2017[4]标准两者计算结果无明显差异。当建筑时间常数较小时，采用Corrado 和Fabrizio[7]，Kokogiannakis 等人[9]和Bruno 等人[10]给出的常数值计算得到的得热或散热利用系数明显高于PHPP 软件默认常数值和EN ISO 52016-2017[4]标准的结果，因此采用这三组模型常数计算得到的采暖空调能源需求绝对值小于采用PHPP 软件默认常数值和EN ISO 52016-2017 标准的计算值。随着建筑时间常数的增加，表1 中五组模型常数值计算得到的得热或散热利用系数的差异逐渐减小。当建筑时间常数大于等于168 h 时，五组模型常数值对得热或散热利用系数的影响很小，可以忽略不计，从表4～表6 可以看出建筑时间常数大于等于168 h 时，不同模型常数值计算得到的采暖空调能源需求差异很小，最大偏差仅为1.78%。

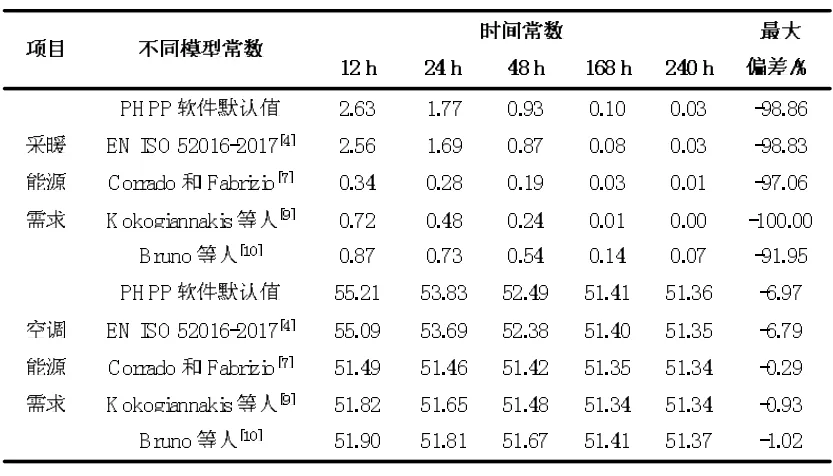
表6 广州地区办公建筑空调能源需求计算值/kWh/(m2·a)

因此，在建筑时间常数较小时，优化月能量平衡算法的模型常数取值，可以提高月能量平衡算法的准确性。当建筑时间常数较大时，优化模型常数取值对月能量平衡算法的准确性影响较小，此时要进一步提高月能量平衡算法的准确性，需进一步研究建筑的传热和内热分布等对得热量和散热量计算的影响。

4 结论

在进行建筑能效评定和超低能耗建筑认证时，月能量平衡算法被广泛用于计算建筑的年内采暖空调能源需求。针对文献中给出的五组模型常数值，本文计算三个气候区不同建筑时间常数下办公建筑的采暖空调能源需求。研究发现，除广州地区采暖能源需求绝对值较小，可以忽略以外，采用PHPP软件默认常数值和EN ISO 52016-2017标准给出的模型常数值时，建筑时间常数对建筑采暖、空调能源需求的影响较为显著，相对偏差分别为18.16%～32.22%和6.79%～22.23%；而采用文献中其他三组优化后的模型常数值时，建筑时间常数对建筑采暖空调能源需求的影响较小，分别为1.64%～11.34%和0.16%～3.12%。

当建筑时间常数较小时，月能量平衡算法的模型常数取值对得热利用系数和散热利用系数的影响较为显著。当建筑时间常数大于168 h 时，模型常数取值的影响可以忽略不计。因此当建筑时间常数较小时，优化月能量平衡算法的模型常数取值可以提高该算法的准确性。当建筑时间常数较大时，优化模型常数取值不能进一步提高该算法的准确性。