基于点云数据的齿轮副啮合接触应力研究

2021-07-28王茜，黎振，陈鹏，刘鑫

天津职业技术师范大学学报 2021年2期

王茜，黎振，陈鹏，刘鑫

（1.天津职业技术师范大学汽车模具智能制造技术国家地方联合工程实验室，天津300222；2.天津职业技术师范大学天津市高速切削与精密加工重点实验室，天津300222）

齿轮是不可或缺的零件，在高铁、机床、航母、飞机等制造领域有着广泛的应用，在现代工业发展中占有重要地位。在齿轮传动中，直齿圆柱齿轮是一种常见的齿轮，其具有齿形易于加工、传动比较高、安装误差不敏感、寿命长等优点，被广泛应用于机械传动中[1]。在实际工况下，齿轮常常因受冲击载荷、齿面受力不均等问题而磨损甚至失效，所以对齿轮的啮合传动过程进行分析具有一定的实际工程价值[2]。同时，齿轮传动是机械传动装置中最重要、应用最广泛的一种[3]，因此齿轮的损伤和失效也备受人们的关注。

在当前齿轮抗疲劳设计中接触疲劳问题日益突出。研究者对齿轮的微观形貌、齿廓的变化、齿面的硬度进行了实验检测、疲劳寿命分析与预测[4-5]。其中，平键[6]对直齿啮合齿轮接触变形位移、动载荷系数等参数进行了仿真分析。袁飞[7]论述了齿面磨损对轮齿接触能力及时变啮合刚度的影响。Zhou等[8]研究了微观组织、夹杂物和表面粗糙度对齿轮接触疲劳行为的影响。啮合状态中，齿轮的接触应力大小是衡量接触疲劳大小的主要因素，除了齿轮齿面自身的微观性能之外，在传动系统中，零件的加工误差、安装误差和弹性变形都会影响其传动精度和齿面接触性能[9-10]。国外很多学者对轮齿接触应力的计算问题也进行了不同方向的研究[11-14]。

研究者们采用各种实验技术和手段探究齿轮失效的主要影响因素，而在基于逆向技术对实体齿轮进行接触状态的预判方面鲜有报道。由于齿轮每个齿加工精度的差异，导致齿轮副配合齿的不同，其全齿的接触状态差异巨大，从而影响齿轮服役过程的寿命。因此，对齿轮副工作过程的接触状态进行预判，并对啮合齿进行优化设计，对提高齿轮副服役过程稳定性及寿命具有重要意义。本文针对实际齿轮副误差导致服役过程接触应力波动的问题，以齿轮副高精度点云数据为基础，分析不同初始啮合齿轮条件下的全周接触应力，提出根据齿轮副实际加工精度优化初始啮合齿，以提高齿轮服役过程中的稳定性和延长疲劳寿命。

1 直齿圆柱齿轮的数据采集和齿廓精度分析

1.1 直齿圆柱齿轮的三维建模和数据采集

首先对传动齿轮进行设计与加工。所设计研究的两齿轮副的传动比取i12=4/3，齿轮副设计参数如表1所示。根据数据进行计算机建模及试样的加工，得到试样齿轮。两齿轮加工选用的材料为20CrNiMo，弹性模量E=210 Pa，泊松比μ=0.3，屈服强度=785 MPa。

表1 齿轮副设计参数

为了获得试样齿轮的尺寸数据，利用ATOSCompact Scan三维扫描仪对试样齿轮进行三维扫描，得到精确的齿轮点云数据。

1.2 齿轮的基本尺寸检测

将获取的齿轮点云数据放到GOM Inspect软件中进行检测分析。分析齿轮的齿廓精度，并对齿轮的基本尺寸、形位公差、周节尺寸、节点位置、单次转动角度等进行测量，获得相关的尺寸精度。

对大齿轮的28个齿进行编号，分别为ZA1—ZA28，对小齿轮的21个齿进行编号，分别为ZB1—ZB21。两齿轮基本尺寸检测如图1所示。从图1可知，齿轮的实际直径尺寸与标称尺寸存在偏差。齿轮齿根圆和齿顶圆数据检测如表2所示。

图1 两齿轮基本尺寸检测

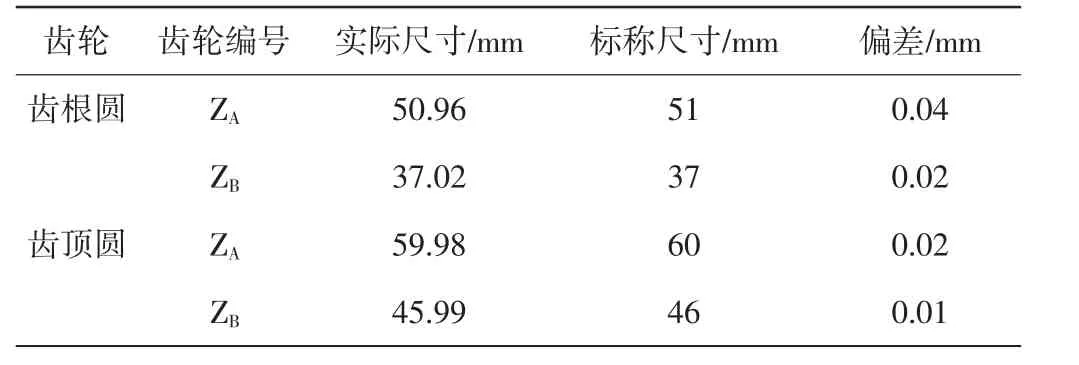
表2 齿轮齿根圆和齿顶圆数据检测

1.3 齿轮啮合过程节点位置误差检测

对两齿轮在啮合过程中节点位置进行齿面的误差检测，检测图如图2所示。从图2可知，大齿轮最大误差为-0.20 mm，最小为+0.01 mm。两齿轮啮合过程节点位置误差汇总如表3所示。

表3 两齿轮啮合过程节点位置误差汇总mm

图2 两齿轮节点位置误差检测图

1.4 齿轮的周节误差检测

对两齿轮进行周节误差检测，齿轮的周节误差汇总如表4所示。从表4可知，两齿轮周节误差最大为0.045 1 mm，最小为0.000 3 mm。

表4 齿轮的周节误差汇总mm

1.5 齿轮的转动角度检测

齿轮啮合过程中，两齿轮从上一节点到下一节点会有转动角度，在对比理论转动角度的基础上，分别对两齿轮的转动角度做检测，齿轮转动角度误差汇总如表5所示。从表5可知，最大误差为0.098 9°，最小误差为0.000 3°。

2 直齿圆柱齿轮传动齿面接触应力的计算

在研究齿轮的啮合过程中，通常应用赫兹接触理论，在实际计算疲劳强度的过程中，经常取啮合节点位置处的接触应力作为计算和分析的参考依据。对直齿圆柱齿轮的齿面接触强度的计算公式进行简化，使用一对轴线相互平行的圆柱体模拟其传动。当圆柱体受到压力而相互接触作用时，接触形式为面接触，由此产生的最大接触应力位于接触区域中线。对应的接触强度计算式为

式中：σH为接触应力（MPa）；Fn为法向力（N）；L为接触线长度（mm）；1/ρε为综合曲率；ZE为弹性系数，经查该齿轮弹性系数ZE=191.6。

根据弹性力学理论，任意形状的2个曲面接触点的主曲率均与接触点的接触应力与变形大小有关，因此对接触点的主曲率进行计算[15]。综合曲率半径由GOM软件拟合得出，啮合点综合曲率拟合如图3所示。

图3 啮合点综合曲率拟合

采用系统抽样法取其中的ZB1、ZB7、ZB14、ZB21与ZA1作为啮合初始状态分别进行分析。

将小齿轮各齿的接触线长度设为定值，分析各轮齿的曲率半径和接触应力。基于点云数据，对啮合过程中的经过拟合可以得出，小齿轮的各轮齿分别在节点处进行综合曲率半径拟合。法向力Fn取100 N，接触线长度L取定值20 mm，代入式（1）进行计算，可以得出齿轮副啮合过程中各齿在节点位置的接触应力大小。综合曲率与接触应力如表6所示。

表6 综合曲率与接触应力

从表6可知4种初始状态下进行拟合分析后所获得的综合曲率与接触应力的平均值和极差值。由于综合曲率的不同以及受加工精度的影响，各个轮齿在节点处的接触应力也不同。

各初始状态下，齿轮传动产生的接触应力相差不大。当ZA1与ZB1啮合时，齿轮传动所产生的接触应力的极差值最大为11.25 MPa，此时的齿轮传动最不稳定，而ZA1与ZB21为初始状态的传动其接触应力范围最小为4.34 MPa。此时的齿轮传动最稳定。

设置综合曲率为定值分析各齿的接触应力。对啮合过程中小齿轮在节点位置啮合的接触线长度进行测量。选取误差值为0.1 mm，分别对各齿接触线长度进行测量，接触线长度测量示意图如图4所示。综合曲率取表6所列的平均值，法向力Fn取100 N，再根据式（1）进行计算，可以得出啮合过程中小齿轮的21个齿在各啮合初始状态下节点位置的接触应力大小。接触线长度与接触应力值如表7所示。

图4 接触线长度测量示意图

表7 接触线长度与接触应力值

从表7可知4种不同啮合状态下接触线长度与接触应力的平均值和极差值。不同初始状态啮合下，接触线长度不同，接触应力也会随之变化。

相对于表6，此时的齿轮传动所产生的应力极差变大，传动较为不稳定。当ZA1与ZB7啮合时所产生的接触应力的极差值最大，为272.53 MPa，由此看出，齿轮啮合时接触线长度大小对接触应力的影响较大。

同时考虑综合曲率和接触线长度，得出啮合过程中齿轮全周各齿在节点位置的接触应力大小。齿轮全周接触线长度变化曲线图和接触应力变化曲线图分别如图5和图6所示。

图5 齿轮全周接触线长度变化曲线图

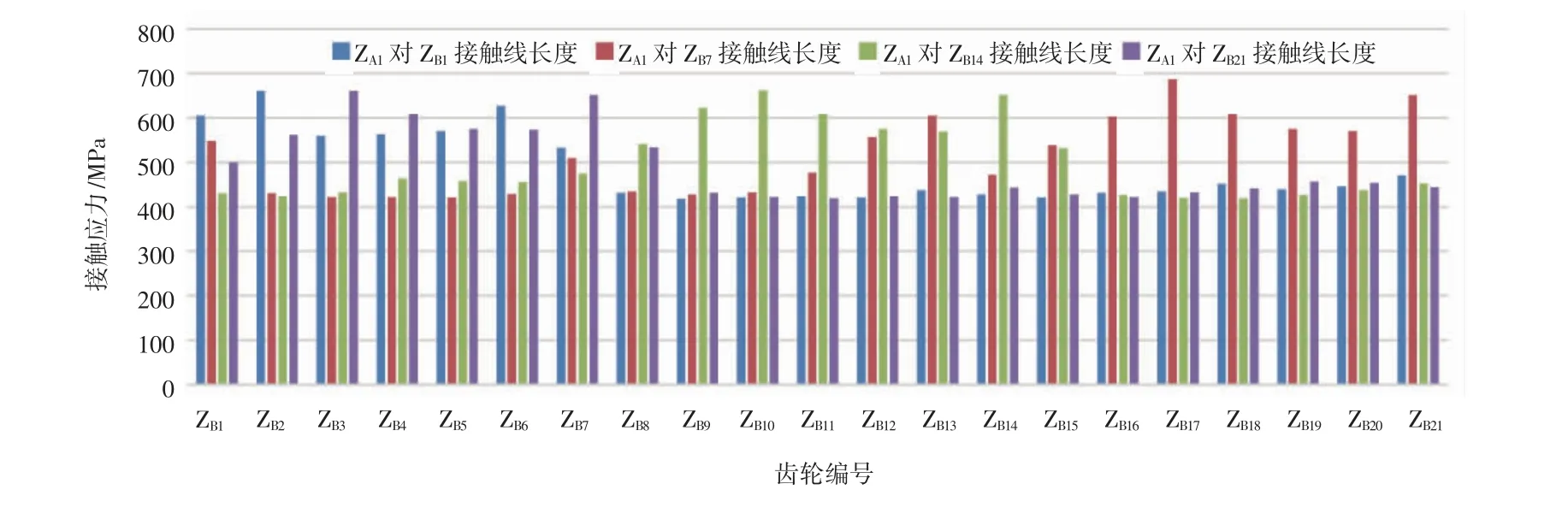
图6 齿轮全周接触应力变化曲线图

综合曲率、接触线长度与接触应力如表8所示。从表8可知4种不同初始状态下接触应力随综合曲率以及接触线长度的变化而变化所对应的各平均值和极差值。可以看出，不同初始状态啮合下，由于综合曲率和接触线长度的变化，接触应力有所不同。

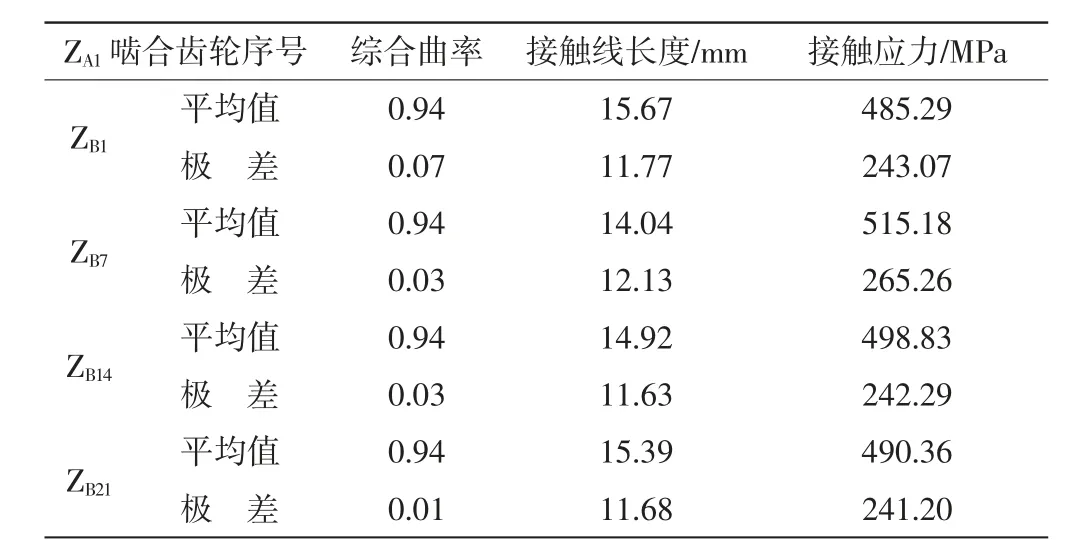
表8 综合曲率、接触线长度与接触应力

测量数据发现，当ZA1与ZB7啮合时，齿轮的接触应力的波动最大，传动最不稳定。

通过分别观察4种初始状态下接触应力随综合曲率、接触线长度、综合曲率和接触线长度变化而变化的规律，3种情况进行对比可以看出，当综合曲率和接触线长度均变化时，接触应力的极差值明显增大，传动不平稳。

综合齿轮齿廓误差分析，以小齿轮为例，可以看出节点误差最大在ZB17，但在4种初始啮合状态下最大的接触应力仅有1次在ZB17的位置，节点误差最小的在ZB6，4种初始啮合状态下最小的接触应力不在ZB6；周节误差最大在ZB12，4种初始啮合状态下，最大的接触应力均不在ZB12，周节误差最小在ZB21，4种初始啮合状态下，最小的接触应力却不在ZB21；转动角度的误差最大在ZB8，但4种初始啮合状态下，最大的接触应力均不在ZB8；误差最小在ZB12，但4种初始啮合状态下，最大的接触应力均不在ZB12。由此可见，齿廓误差最大（小）的齿并不一定是接触应力最大（小）的齿。因此，对齿轮副工作过程的接触状态进行预判意义重大。