基于最小二乘的FGR低氮燃烧自适应算法

吴彭江 傅铁华

(1.绍兴市能源检测院,浙江绍兴 312071;2.绍兴市特种设备检测院,浙江绍兴 312071)

0 引言

为了分析、研究及控制燃气锅炉FGR系统[1-2],必须先建立一个动态系统的数学模型,然而,实际对象的动力学特性基本上是未知的,许多情况下控制、预测需要采用辨识技术,实现自适应控制、信号处理等。常见的方法是从系统采集一批数据,得到有关系统特性的信息,然后用离线的方式分析这批数据,建立系统的模型。但是,燃气锅炉FGR低氮控制系统实际上是时变的,此时比较理想的做法是利用在线辨识来更新系统参数。自适应估计就是在期望信号不完全或完全未知情况下,只根据观测信号值来解决估计问题的一些方法。

最小二乘(LS)算法不需要任何先验知识,只需要关于被估计量的观测信号模型,即可实现信号参量的估计,且算法简单,易于实现,在工业控制领域被广泛使用。但是FGR控制系统的动态特性随时间会发生变化,常规最小二乘算法的“数据饱和”现象会使算法慢慢失去修正能力,以致难以有效跟踪时变参数。

1 时变遗忘因子和加权配合的递推辨识算法

文献[3]从被控对象连续传递函数出发,经离散化处理得到差分方程,通过极小化指标函数,得出定常系统的最小二乘递推辨识算法,并比较了常规PID控制和RLS控制的性能。本文在文献[3]基础上,引入遗忘因子和加权因子,给出时变遗忘因子和加权配合的递推辨识算法。

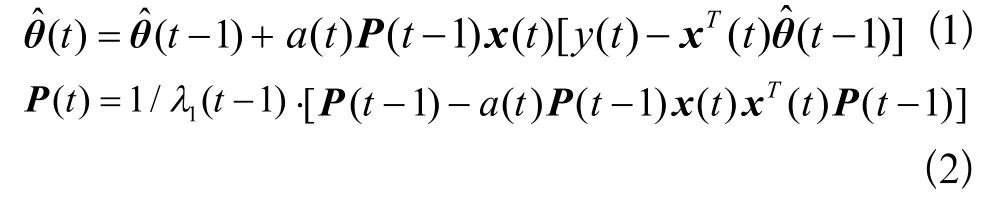
其中λ1(t)、λ2(t)分别为t时刻的遗忘因子和加权因子,且满足0＜λ1min≤λ1(t )≤λ1max≤1,0＜λ2min≤λ2(t)≤λ2max＜∞。

式(1)、(2)还可写成

2 算法性质

记t时刻的参数估计误差和输出误差分别为:

对于时变系统线性回归模型

算法(1)～(3)有下列性质

其中, ρ0为P-1(0)的条件数、λminP-1(0)分别为P-1(0)的最大、最小特征值。

其中γ0=λmaxP(0),即P(0)的最大特征值。

证明:由式(8)、(1)、(6),可知

再由(5)式,知

定义Lyapunov函数

由式(9)、(10)及上式,知

由于0＜λ1(t)≤1,所以

且有

由式(5)知

由不等式(14)、(15)知

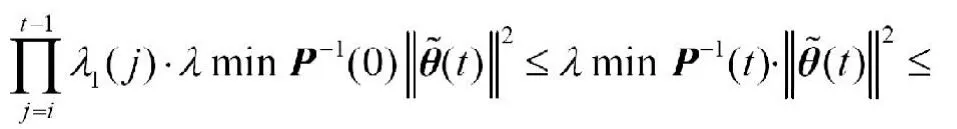
由上式可得性质1。

再定义函数

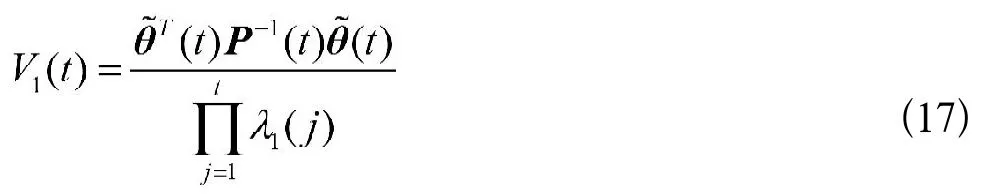
由式(17)和式(10)知

可见,V1(t)为非负的不增函数。对式(18)从1加到N,知

因为V1(N) 是非负的,所以性质2成立。

由V1(t)的收敛性及性质2可知

再由(15)式易知

有

由式(19)和式(21)可得性质3。

注意到

由性质2及上式可得性质4。

由算法(1)和不等式(20)知

由上式及性质4可知性质5成立。

由于

再由Schwarz不等式,知

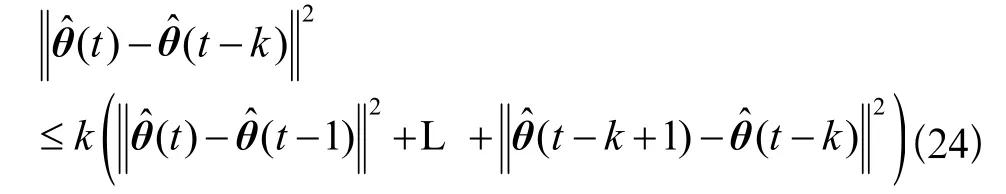
因为k为有限数,所以由性质5及式(24)可得性质6。

由性质6可直接得到性质7。

3 指数收敛性

定义算法被称为是指数收敛的,则应存在γ＞0和 0＜p≤1使得:

文中算法(1)～(3)具有指数收敛性,证明略。

4 计算机仿真

考虑如下确定性离散FGR控制系统。

式中a=-1.6,b=2.8,｛v(t)｝为零均值,方差σ2=0.12的随机噪声序列。

分别用常规负荷调节法(LAM)和递推最小二乘算法(RLS)对系统进行控制,采样数据长度取800。锅炉负荷设定为:

在变化负荷下,两种FGR低氮控制方法的仿真效果如图1、图2所示。

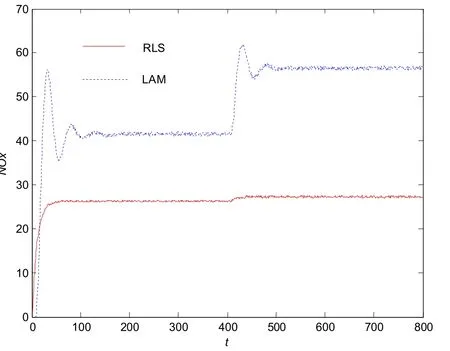
图1 两种控制方法NOX排放仿真效果图Fig.1 The simulation effect diagram of two control methods of NOX emission

图2 变化负荷下的FGR开度控制响应曲线Fig.2 FGR opening control response curve under varying load

从图1可以看出,LAM虽然可以有效抑制NOX的生成,但是随着负荷的升高,NOX也会随之升高,而RLS控制基本不会受负荷的影响,使NOX排放浓度始终控制在预期值。图2则进一步解释了两种方法的差异性,负荷一旦确定,LAM控制的FGR开度是固定不变的,而RLS可以在线实时调节。

5 结语

本文以燃气锅炉低氮燃烧FGR系统为研究对象,探讨了常规负荷调节法(LAM)和带遗忘因子的递推最小二乘算法(RLS)的控制原理,文中重点分析了RLS的一些列重要性质,并给出了其指数收敛性结论。数值仿真结果进一步论证了所提算法在FGR控制系统上的有效性和优越性。