一种用于非均匀网格划分的低数值色散的AA-ID-FDTD方法

2021-07-28刘桂英谢孟洪赵珉陈伟军

数字技术与应用 2021年6期

刘桂英谢孟洪赵珉陈伟军

(岭南师范学院信息工程学院,广东湛江 524048)

0 引言

时域有限差分(FDTD)方法是电磁器件建模的有效方法。然而,由数值离散方法引起的数值色散误差(NDE)影响计算精度,使得仿真结果偏离真实值。为了降低NDE,精细网格FDTD被提出,这无疑增大了计算量。为了改善数值色散,高阶和ID方法被引进FDTD,但在非均匀网格划分技术中仍然存在各向异性数值色散误差。为了避免上述问题,人工各向异性(AA)参数被引进FDTD来抑制各向异性NDE,提高计算精度。因为AA参数只用来改变自由空间介电常数,所以该方法不会增加计算量。

本文提出了一种基于各向同性色散(ID)和人工各向异性(AA)参数的时域有限差分方法来对电磁波在材料中的传播进行建模,该方法取代了传统的以空间各向同性方式对场进行采样的中心有限差分方法。用AA参数来修正自由空间介电常数。文中用一个数值实例对本文提出的方法进行了验证,结果表明对于非均匀网格,本文的AAID-FDTD方法的准确性要高于ID-FDTD。

1 数学公式

以文献[1]提出的ID-FDTD方法公式为基础,引入电场人工各向异性参数,2-D TE波的更新函数可以表示为:

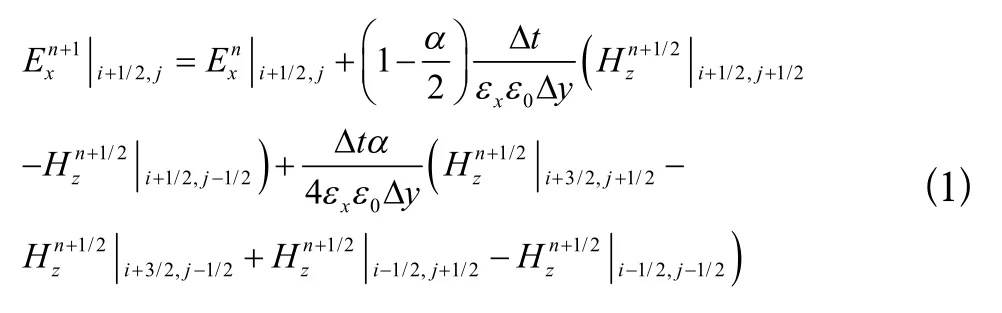
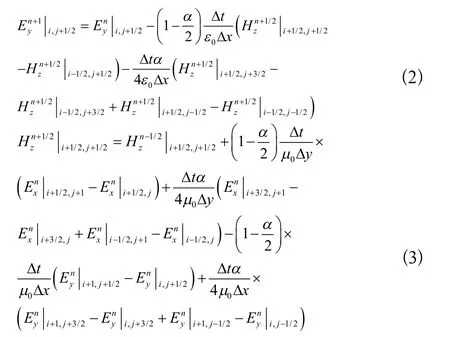
其中ε0和μ0分别表示自由空间的介电系数和磁导系数。εx和εy分别是电场Ex和Ey的人工各向异性参数,Δx和Δy分别是x和y方向的网格尺寸。α是权重系数,角标i和j表示采样点。对于EM波,2-DTEz波的更新函数为:

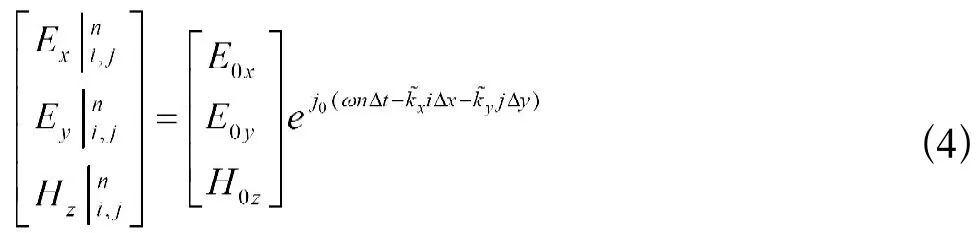
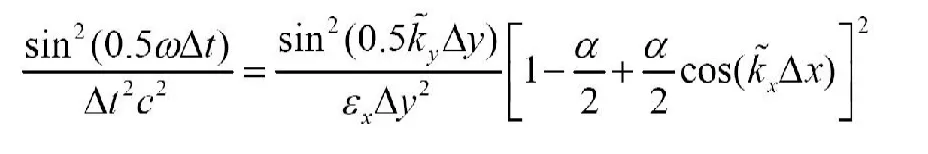
如文献[2],定义单个FDTD网格的形状Z和空间分辨系数R为:

假设45φ=°,A=1,(8)可以写成:

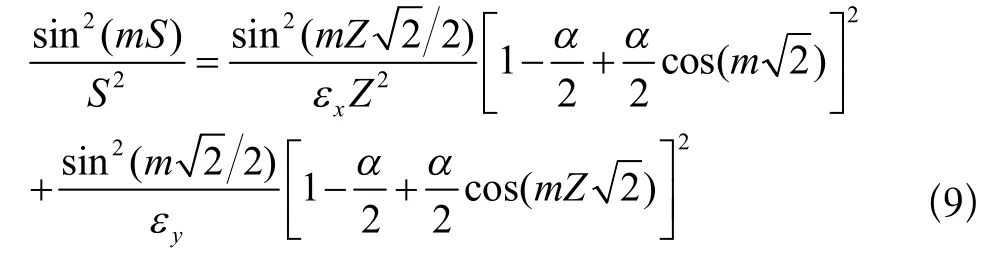
利用牛顿迭代公式,由(9)可以得到权重系数α的结果。

图1为不加AA参数时权重系数相对于空间分辨率R的关系,由图1可以看出对于不同的Z,α趋于不同的常数。图2为加上AA参数时权重系数相对于空间分辨率R的关系。由图2可以看出对于不同的Z,α都趋于同一常数(0.1667)。

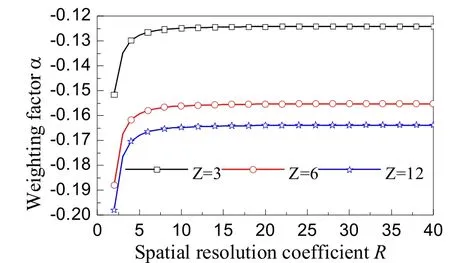
图1 没有人工各向异性参数情况下,权重因子与空间分辨率系数的关系图(S=0.8)Fig.1 Weighting factor α versus spatial resolution coefficient R without AA parameters. S=0.8 for all of the cases

图2 有人工各向异性参数情况下,权重因子与空间分辨率系数的关系图(S=0.8)Fig.2 Weighting factor α versus spatial resolution coefficient R with AA parameters. S=0.8 for all of the cases

图3表明相对数值速度A是波传播角度φ的函数。由图可以看出,在没加人工各向异性参数时,在空间分辨系数R为常数的情况下,随着Z的增大,波传播角度φ的函数相对数值速度也变大。当加入人工各向异性参数时,可以到,当Z取值为3,6,12时,数值色散误差都明显降低。

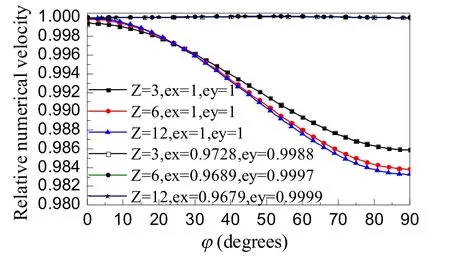
图3 在相同的空间分辨率系数情况下,相对数值速度与波传输角度的关系图(R=10和S=0.8)Fig.3 Variation of relative numerical velocity with wave propagation angle in a 2-D ID-FDTD grid for same spatial resolution coefficient. R=10 and S=0.8 for all of the cases

2 数值结果

为了验证本文所提出方法的性能,以如图4所示的2-D谐振腔为例,计算其中的传输场。以正弦调制的高斯脉冲(14)为信源:

图4 ID-FDTD的计算模型Fig.4 Diagram of computational domain for ID-FDTD

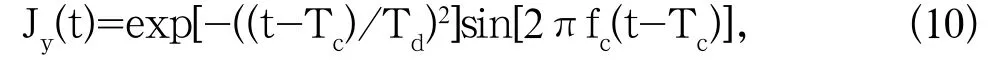
式中,Td=1/(2fc),Tc=3Td,fc=5GHz,持续时间Tf=4ns,时间步长Δt=2×10-13s,仿真时长取20000Δt。在该计算区域内采用300×100的网格,其尺寸大小为0.1×0.1mm2。x轴y轴方向采用良好导电性能的金属边界。分别采用传统的ID-FDTD和本文方法计算其横向电场。

图5显示的是在观察点o (240Δx, 150Δy),用传统的ID-FDTD和本文方法计算的归一化的横向电场的时域波形图。结果显示两种方法及仿真结果一致。

图5 采用文中提出的方法和传统的ID-FDTD方法计算的瞬态电场值Fig.5 Normalized transient electric fields calculated with the conventional ID-FDTD and proposed method

表1为不同方法的计算能力对比。运行该仿真的电脑配置为Intel ® Core (TM) i5-4210 and 8 GB RAM。如表1所示,当采用300×9的网格时,采用本文方法和传统ID方法计算出的相对误差从0.47%降为0.41%,其中本文方法的AA参数取值为ex=0.9119,ey=0.9993。此外,为了验证本文方法的计算精度,用离散傅氏变换求得观测点的谐振频率,谐振频率的相对误差定义为:|fProposedmethodorID-FDTD-freferencesolution|/freferencesolution×100%,其中freferencesolution是采用均匀网格300×300,由现存的ID-FDTD方法求得的谐振频率。 fproposedmethod和fID-FDTD分别是在如表所示非均匀网格划分的情况下,由本文方法和现存ID-FDTD方法所求得的谐振频率。如表1所示,与现存的方法相比,本文方法求得的相对误差更小。