基于任务的k/n(G)系统舰船备件需求预测
2021-07-27刘海涛邵松世张志华
刘海涛, 邵松世, 张志华
(1.海军工程大学基础部, 湖北 武汉 430033; 2.海军工程大学舰船与海洋学院, 湖北 武汉 430033)
0 引 言
舰船备件是确保舰船维修保障活动有效实施、遂行海上任务的重要物质基础。特别是对于大型舰船,一方面由于舰船海上任务时间长、装备运行强度高等原因,备件需求涉及的种类多、数量大;另一方面由于海上补给困难,备件需求还受到舰船自身携行能力、舰上维修条件因素等的影响[1-2]。因此,在深入分析舰船装备维修特点的基础上,发展适合于舰船装备的备件需求预测方法是当前舰船装备维修保障研究的重要内容之一[3-5]。
k/n(G)系统在舰船装备结构设计中有广泛应用,其备件需求预测与资源配置问题受到很多学者关注[6-7]。文献[8]采用有限源排队论获取备件短缺数的概率分布,并通过边际分析算法确定k/n(G)结构系统的备件数量。文献[9]针对舰船编队在航无补给的情况,建立了舰船出航期间设备冗余和外场更换件冗余系统任务成功概率的评估模型,通过瞬时可用度求出了任务成功概率。但上述方法均未考虑定期维修对备件需求的影响。文献[10]则在定期维修模式下,针对故障件批量送修的大型k/n(G)系统资源配置问题,建立了系统平均备件短缺概率模型,但对于执行海上任务的舰船装备而言,其难以满足批量送修对供应链的要求。文献[11-12]通过建立马尔可夫模型研究维修模式对k/n(G)系统备件需求的影响,指出定期维修与事后维修相结合有助于降低维修成本,但所建立模型以系统稳态可用度为决策依据,不适合于舰船装备特点。
事实上,维修模式对备件需求有重要影响[13-14]。对于执行海上任务的舰船装备而言,首先由于备件补给十分困难,海上期间的维修活动主要依赖随舰携行的备件,且以换件维修为主;其次为了提高战备完好性,通常还在出航前的准备阶段对装备进行集中检修,以保证装备的良好初始状态;最后对于k/n(G)系统,当部件故障不影响装备运行时,通常可以选择待海上任务结束后对故障件进行集中修理。由此可见,其维修模式表现为事后维修与任务后检修相结合的特点。
因此,为了更好地描述舰船装备在这一维修模式下的备件需求,本文针对其特点建立备件需求模型,为了方便理解和简化计算,进一步给出需求模型的近似计算方法和工程解释,并对算法有效性进行验证。
1 基本假设与模型准备
考察由n个相互独立工作的相同部件组成的k/n(G)系统,即当且仅当正常工作部件不少于k个时,系统正常工作。为了更好地建立备件需求模型,提出如下假设。
假设 1在执行海上任务期间,采取事后维修与任务后检修相结合的维修模式,即在执行海上任务之前,对舰船装备进行集中检修,保证舰船装备完好状态。在执行海上任务过程中,采取事后维修方式,即当部件故障不影响系统工作时,不进行维修,系统故障后立即进行维修。在执行海上任务结束后,集中对舰船装备进行任务后检修,恢复装备的正常状态。
假设 2不考虑事后维修的维修时间。在舰船执行海上任务期间,通常采取换件维修的方式,由于与任务时间相比,换件维修所需时间极少,因此维修时间暂且忽略不计。
假设 3各部件独立工作,且寿命均服从指数分布E(λ)。指数分布大量存在于舰船装备中,如印制电路板插件、电子部件、电阻、电容、集成电路等电子类装备,因此本文针对部件寿命服从指数分布的情况建立备件需求模型,即部件寿命T的概率密度为
(1)
寿命分布函数为
F(t)=1-e-λ t,t≥0
(2)
可靠度函数为
R(t)=1-F(t)=e-λ t,t≥0
(3)
由式(3)可知,k/n(G)系统的可靠度函数为
(4)
假设 4不考虑备件补给。由于海上补给困难,因此假设海上期间系统故障维修所需备件均来自于舰船自身携带。


图1 一个任务期内事后维修与任务后检修示意图
2 舰船备件需求的概率分布及特征
在一个海上任务周期[0,T0]内,记备件需求量为随机变量N,如图1所示,该需求量包含事后维修和任务后检修所需备件,但不包含任务前检修所需备件。显然,需求量N是一个取非负整数的随机变量,本节研究N的概率分布及特征。
2.1 N首先分析故障特点:在周期[0,T0]内,当N例如,由于N=0表示k/n(G)系统工作到T0时所有部件均未发生故障,因此利用式(3)可知:
P(N=0)=R(T0)…R(T0)=exp(-nλT0)
(5)
类似地,由于N=1表示k/n(G)系统工作到T0时有1个部件发生故障,系统仍正常工作,备件需求发生在任务后检修时刻,因此
nexp[-(n-1)λT0][1-exp(-λT0)]
(6)
以此类推,由于N=n-k表示k/n(G)系统工作到T0时有n-k个部件发生故障,系统无故障,因此
(7)
综合式(5)~式(7)可得,当j=0,1,…,n-k时,有
(8)
2.2 n -k+1≤N≤2(n -k)+1时的概率分布
当n-k+1≤N≤2(n-k)+1时,部件故障特点为:①当故障数达到n-k+1时,正常部件个数低于k,因此系统发生故障,需要进行事后维修,维修后所有部件均正常工作;②当故障数再增加n-k个,即故障数达到2(n-k)+1时,由于系统仍有k个部件正常工作,因此不需维修。
由此可见,n-k+1≤N≤2(n-k)+1表示系统在[0,T0]内有且仅有1次故障。根据上述特点,可以利用概率元法[15-16]求出n-k+1≤N≤2(n-k)+1时的概率分布。
例如,由于N=n-k+1表示k/n(G)系统工作到T0时部件故障次数为n-k+1,因此记第n-k+1次部件故障发生时刻为t,则系统在t时刻发生故障,此时需对系统中所有故障部件进行更换,更换后在[t,T0]内不再有部件发生故障。因此,[0,T0]周期内的部件故障情况如图2所示。

图2 一个任务期内有n-k+1个部件故障示意图
接下来求P(N=n-k+1)。首先,在[0,t]内有n-k个部件发生故障的概率为
(9)
然后,在t时刻,由于系统仅有k个部件正常工作,因此利用指数分布的“无记忆性”可知,在[t,t+dt]内有1个部件发生故障的概率为
(10)
最后,在t+dt时刻,由于已经对系统中故障部件进行了更换,即所有部件均正常工作,因此在[t+dt,T0]内无部件发生故障的概率为
P(N(t,T0)=0)=e-nλ(T0-t)
(11)
综合式(9)~式(11),可得
P(N=n-k+1)=
(12)
以此类推,可以求出当j=1,2,…,n-k时,系统在[0,T0]周期内发生n-k+1+j次故障的概率。
事实上,由于N=n-k+1+j表示系统在[0,t]内有n-k个部件发生故障、在[t,t+dt]内有1个部件发生故障、在[t+dt,T0]内有j个部件发生故障,因此其故障情况如图3所示。

图3 一个任务期内有n-k+1+j个部件故障示意图
由此可见,当j=1,2,…,n-k时,
P(N=n-k+1+j)=
(13)
式中:P(N(t,T0)=j)表示在[t+dt,T0]内有j个部件发生故障的概率。
又因为在t+dt时刻所有部件均正常工作,因此,
(14)
将式(9)、式(10)和式(14)代入式(13),当j=1,2,…,n-k时,整理得
P(N=n-k+1+j)=
(15)
综合式(12)和式(15),当n-k+1≤N≤2(n-k)+1,j=0,1,2,…,n-k时,备件需求N的概率分布为
P(N=n-k+1+j)=
(16)
2.3 N>2(n -k)+1时的概率分布
当N>2(n-k)+1时,可仿照第2.2节思路求备件需求N的概率分布。但考虑到对于具备冗余设计的k/n(G)系统,一方面随着技术、工艺和管理水平的提高,系统在一个海上任务期内故障大于1的概率应较小;另一方面从装备保障实践来看,在一个海上任务期内同一装备发生两次故障的情况确实极少,因此可以将备件需求N>2(n-k)+1的概率进行合并,即
(17)
综合第2.1~第2.3节可知,在事后维修与任务后检修相结合的维修模式下,备件需求的概率分布可以由式(8)、式(16)和式(17)共同描述。
2.4 需求分布的特征
利用备件需求的概率分布,可以求出在[0,T0]周期内备件需求的相关数字特征。
(1)备件需求的一、二阶矩
在[0,T0]周期内的备件需求的期望为
(18)
方差为
(19)
二阶原点矩为
(20)
(2)平均维修间隔时间
记k/n(G)系统的寿命为Ts,系统两次维修间的间隔时间为随机变量Y,根据海上任务时间T0可知:
(21)
因此,维修间隔时间的分布函数可表示为
(22)
由此可知,维修间隔时间的期望,即平均维修间隔时间为
E(Y)=E(Y|Ts>T0)P(Ts>T0)+
E(Y|Ts≤T0)P(Ts(23)
代入式(4),整理可得
(24)
(3)平均维修次数
利用维修平均间隔时间E(Y),可以得到在[0,T0]周期内的平均维修次数为
(25)
(4)一次维修的平均备件需求量
利用平均维修次数RT0和备件需求的期望E(N),可以得到在[0,T0]周期内一次维修平均备件需求量为
(26)
3 舰船备件需求的近似计算方法
由第2节可知,基于事后维修与任务后检修的备件需求模型可以更加准确地反映k/n(G)系统在一次海上任务期内的备件需求。但由于需求模型较复杂,备件需求的概率分布大多用积分形式表示且计算复杂,不便于理解和使用。为此,本节研究随舰备件需求的近似计算方法并给出需求模型的工程解释。
3.1 基本思路
考察某装舰数为1的伽马型部件,其寿命TG服从Gamma分布,TG~Gamma(a,b),概率密度函数为
(27)
分布函数为
(28)
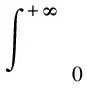
首先,对于装舰数为1的伽马型部件,由文献[17-18]可知,部件与其所配置的备件组成冷储备系统,因此利用Gamma分布的可加性,其备件需求的计算较为容易,满足快速计算的要求。
其次,Gamma分布具有良好的适应性,即当参数取不同值时可以反映不同分布类型,当a为正整数时,f(x)是爱尔兰分布;进一步,当a=1时,f(x)是指数分布。
因此近似计算的基本思路是:若通过适当选取伽马型备件参数a和b的取值,使得其备件需求与基于事后维修和任务后检修的备件需求近似相同,则可以将伽马型备件的备件需求近似作为基于事后维修与任务后检修的备件需求。
3.2 近似计算模型及其工程解释
由第3.1节基本思路可知,近似计算模型的核心在于如何确定Gamma分布中参数a和b的值,使得伽马型备件需求与真实需求近似一致。本节首先给出近似计算模型,即参数a和b取值的确定方法,然后分析模型的工程解释。
(1)近似计算模型
记k/n(G)系统在事后维修与任务后检修相结合维修模式下的备件需求N的分布列为
P(N=j)=pj,j=0,1,2,…
(29)
N的期望和方差如式(18)和式(19)所示。
另一方面,对于装舰数为1的伽马型部件,记其备件需求NG的分布列为
(30)
NG的期望和方差分别表示为
(31)
(32)
显然,式(29)代表k/n(G)系统在事后维修与任务后检修相结合条件下的真实备件需求,可以利用第2节所建模型进行计算,但模型较复杂,不便于理解和使用。
而式(31)表示装舰数为1的伽马型部件在相同任务时间内的备件需求,且计算简单。由文献[18]可知,当j=0,1,2,…时,
(33)
式中:G(j)(T0)表示Gamma分布的j重卷积,即

进一步地,由于当分布列相同时,两者的一、二阶矩也必然相同,因此近似计算模型也可表示为
(34)
参数a和b的取值也可由式(34)确定。
(2)模型的工程解释
由式(27)可知,当a=1时,Gamma分布退化为指数分布,参数b即为该指数型备件的失效率。容易计算在[0,T0]内的备件平均需求为
E(NE)=bT0
(35)
而在事后维修与任务后检修相结合的维修模式下,k/n(G)系统在[0,T0]内的备件平均需求E(N)可表示为
(36)
式中:E(NR)为k/n(G)系统在一次维修活动中的平均备件需求量;T0/E(Y)为[0,T0]内的平均维修次数。
由此可见,作为Gamma分布的一个特例,若采用指数型备件进行近似需求计算,则式(34)变为
(37)
观察式(37)可以发现:一方面,参数b反映指数型备件的失效率;另一方面,在事后维修与任务后检修相结合的模式下,由于E(Y)表示维修平均间隔时间,E(NR)表示在一次维修活动中的备件需求量,因此E(NR)/E(Y)恰好反映了k/n(G)系统在一个工作周期内的失效率。
因此,式(37)本质上反映了当采用指数型备件作为近似需求时,核心在于利用E(NR)/E(Y)对指数型备件的失效率进行调整,而E(NR)/E(Y)恰好反映了在事后维修与任务后检修相结合维修模式下的备件失效率。
实际计算发现,采用式(37)进行近似计算具备较高精度,因此作为更一般情形,式(34)表示的近似计算模型是合理的。
需要注意的是,在式(37)中,平均维修间隔时间E(Y)可以利用式(24)直接计算,但第2节给出的E(NR)计算方法较为复杂。为此,接下来给出一种E(NR)的快速估算方法。
根据全概率公式,一次维修的平均备件需求量E(NR)可近似表示为
E(NR)≐E(NR|Ts>T0)P(Ts>T0)+
E(NR|Ts≤T0)P(Ts式中:E(NR|Ts≤T0)=n-k。
由式(4)可知,
(38)
(39)
又因为当j=0,1,2,…,n-k+1时,
(40)
因此,
E(NR|Ts>T0)P(Ts>T0)=
(41)
由此可见,E(NR)可表示为
(1-Rs(T0))(n-k)
(42)
3.3 算法设计
根据第3.2节的近似计算模型,随舰备件需求近似算法流程如下。
输入舰船任务时间长度T0,k/n(G)系统参数k和n,备件失效率λ。
输出备件需求分布列P(N=j)=pj,平均需求量E(N)。
步骤 1根据式(37)设定伽马型备件参数:即a=1,b=E(NR)/E(Y),其中E(Y)由式(24)确定,E(NR)由式(42)确定。
步骤 2利用式(33)计算伽马型备件需求分布列:
P{NG=j}=G(j)(T0)-G(j+1)(T0)
步骤 3将伽马型备件需求分布近似作为备件需求真实分布,即令
P(N=j)=P{NG=j}
步骤 4利用式(18)计算备件需求平均需求量E(N):
4 算法验证
为验证近似算法的精度,首先依据工程背景设定备件失效率、任务时间、k/n(G)系统等初始参数。然后,利用第3节近似算法计算备件需求的近似分布及分布特征。接下来,根据第2节建立的备件需求模型计算备件需求的真实分布和分布特征。最后,比较二者的近似程度。具体步骤如下。
步骤 1初始参数设定:依据工程背景,在适当范围内设定参数λ、T0、k和n的取值。
步骤 2伽马型备件参数的确定:利用式(37)计算伽马型备件参数a和b的值。
步骤 3伽马型备件需求分布及特征的计算:
利用式(33)计算该伽马型备件需求的分布,记为
利用式(31)计算该伽马型备件的平均需求量。
步骤 4真实备件需求分布及特征的计算:
利用式(8)、式(16)和式(17),计算备件需求的真实分布,记为
P(N=j)=pj,j=0,1,2,…
利用式(18)计算备件的真实平均需求量。
步骤 5误差比较:定义需求分布的平均误差为
(43)
平均备件需求相对误差为
(44)
例如,取定λ=0.000 1,T0=1 000,k=2,n=4,利用式(37)计算得到a=1,b=3.858 3×10-4。进一步,利用式(31)和式(33)计算得到,伽马型备件需求分布如表1所示,平均需求量为E(NG)=0.385 8。另一方面,利用式(8)、式(16)~式(18)计算得到备件需求真实分布,如表2所示,平均需求量为E(N)=0.380 6。

表1 伽马型备件需求分布

表2 伽马型备件需求真实分布
利用式(43)和式(44)计算得到,需求分布的平均误差为error1=0.006 6,备件平均需求量的相对误差为error2=0.013 0,近似分布误差的整体情况如图4所示。可以看到,对于上述取定的参数,基于Gamma分布的舰船备件需求近似算法具有良好精度。

图4 在取定参数下备件需求分布误差示意图
接下来,取定k=2,n=4,改变参数λ和T0的取值,计算结果如表3所示。
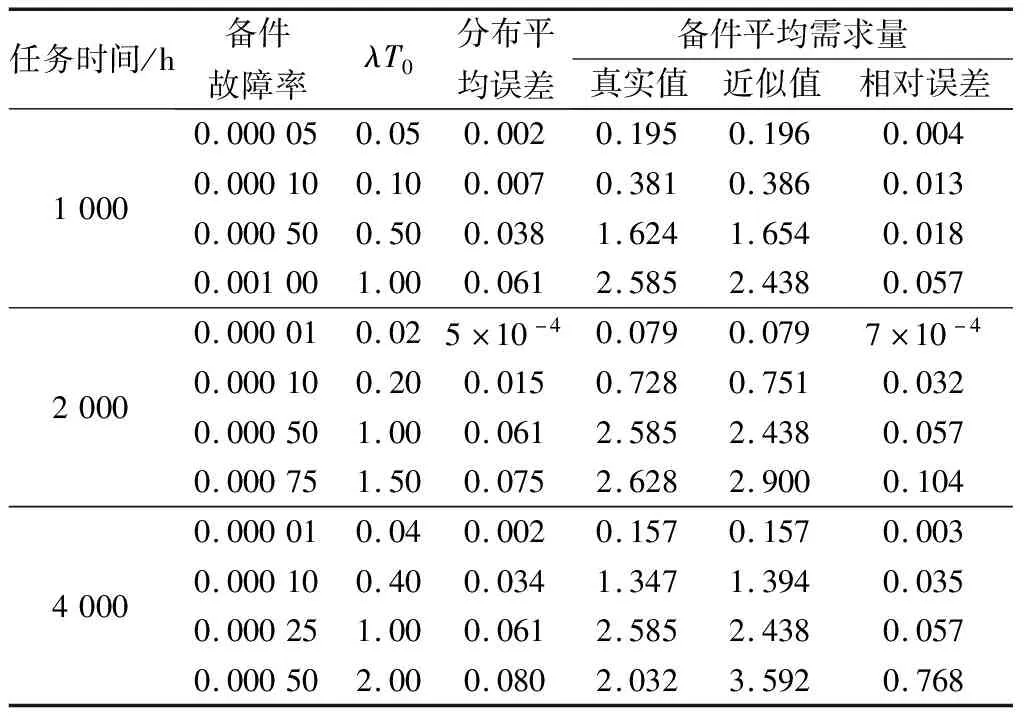
表3 2/4(G)系统在不同参数下的近似结果(k=2,n=4)
观察表3,可以发现如下规律。
(1)当λT0较小(≤1)时,需求分布误差和平均需求误差均较小,这说明近似算法在λT0≤1具有良好的精度。
(2)整体上随着λT0的增大,需求分布误差和平均需求误差均呈现增大的趋势。特别当λT0=2时,误差达到了76.8%,保守起见,当λT0>1时,不应采取近似算法,而使用第2节所建立模型直接计算。
(3)从备件保障实践来看,通过调研发现:实际中λT0超过1的部件项数极少,仅占5%左右,因此近似算法适用于绝大部分备件需求计算问题。
(4)当λT0不变,如表3中λT0=1时,参数λ和T0的变化不影响备件需求。
综上所述,为了进一步验证近似算法的精度,接下来分别针对λT0≤1和参数k、n的典型取值进行计算,结果如表4所示。

表4 k/n(G)系统在不同参数下的计算结果
观察表4可以看到,当λT0≤1时,备件需求的近似计算方法整体上具有较高的精度,满足近似计算的需要。
5 结 论
随着技术水平的进步和管理水平的提高,舰船海上期间的装备维修保障正逐渐转变为事后维修与任务后检修相结合的模式。本文针对这一维修模式特点,通过建立备件需求模型,对常见的k/n(G)系统在一个任务期内的备件需求进行预测,并提出了较简便的近似计算方法,可以为装备备件保障提供参考。但模型仅给出了系统故障不超过1次时的备件需求,虽适用于95%以上的备件需求预测问题,但采用需求模型对备件需求直接计算仍较复杂,接下来还需进一步对需求分布进行完善。
首先分析故障特点:在周期[0,T0]内,当N 例如,由于N=0表示k/n(G)系统工作到T0时所有部件均未发生故障,因此利用式(3)可知: P(N=0)=R(T0)…R(T0)=exp(-nλT0) (5) 类似地,由于N=1表示k/n(G)系统工作到T0时有1个部件发生故障,系统仍正常工作,备件需求发生在任务后检修时刻,因此 nexp[-(n-1)λT0][1-exp(-λT0)] (6) 以此类推,由于N=n-k表示k/n(G)系统工作到T0时有n-k个部件发生故障,系统无故障,因此 (7) 综合式(5)~式(7)可得,当j=0,1,…,n-k时,有 (8) 当n-k+1≤N≤2(n-k)+1时,部件故障特点为:①当故障数达到n-k+1时,正常部件个数低于k,因此系统发生故障,需要进行事后维修,维修后所有部件均正常工作;②当故障数再增加n-k个,即故障数达到2(n-k)+1时,由于系统仍有k个部件正常工作,因此不需维修。 由此可见,n-k+1≤N≤2(n-k)+1表示系统在[0,T0]内有且仅有1次故障。根据上述特点,可以利用概率元法[15-16]求出n-k+1≤N≤2(n-k)+1时的概率分布。 例如,由于N=n-k+1表示k/n(G)系统工作到T0时部件故障次数为n-k+1,因此记第n-k+1次部件故障发生时刻为t,则系统在t时刻发生故障,此时需对系统中所有故障部件进行更换,更换后在[t,T0]内不再有部件发生故障。因此,[0,T0]周期内的部件故障情况如图2所示。 图2 一个任务期内有n-k+1个部件故障示意图 接下来求P(N=n-k+1)。首先,在[0,t]内有n-k个部件发生故障的概率为 (9) 然后,在t时刻,由于系统仅有k个部件正常工作,因此利用指数分布的“无记忆性”可知,在[t,t+dt]内有1个部件发生故障的概率为 (10) 最后,在t+dt时刻,由于已经对系统中故障部件进行了更换,即所有部件均正常工作,因此在[t+dt,T0]内无部件发生故障的概率为 P(N(t,T0)=0)=e-nλ(T0-t) (11) 综合式(9)~式(11),可得 P(N=n-k+1)= (12) 以此类推,可以求出当j=1,2,…,n-k时,系统在[0,T0]周期内发生n-k+1+j次故障的概率。 事实上,由于N=n-k+1+j表示系统在[0,t]内有n-k个部件发生故障、在[t,t+dt]内有1个部件发生故障、在[t+dt,T0]内有j个部件发生故障,因此其故障情况如图3所示。 图3 一个任务期内有n-k+1+j个部件故障示意图 由此可见,当j=1,2,…,n-k时, P(N=n-k+1+j)= (13) 式中:P(N(t,T0)=j)表示在[t+dt,T0]内有j个部件发生故障的概率。 又因为在t+dt时刻所有部件均正常工作,因此, (14) 将式(9)、式(10)和式(14)代入式(13),当j=1,2,…,n-k时,整理得 P(N=n-k+1+j)= (15) 综合式(12)和式(15),当n-k+1≤N≤2(n-k)+1,j=0,1,2,…,n-k时,备件需求N的概率分布为 P(N=n-k+1+j)= (16) 当N>2(n-k)+1时,可仿照第2.2节思路求备件需求N的概率分布。但考虑到对于具备冗余设计的k/n(G)系统,一方面随着技术、工艺和管理水平的提高,系统在一个海上任务期内故障大于1的概率应较小;另一方面从装备保障实践来看,在一个海上任务期内同一装备发生两次故障的情况确实极少,因此可以将备件需求N>2(n-k)+1的概率进行合并,即 (17) 综合第2.1~第2.3节可知,在事后维修与任务后检修相结合的维修模式下,备件需求的概率分布可以由式(8)、式(16)和式(17)共同描述。 利用备件需求的概率分布,可以求出在[0,T0]周期内备件需求的相关数字特征。 (1)备件需求的一、二阶矩 在[0,T0]周期内的备件需求的期望为 (18) 方差为 (19) 二阶原点矩为 (20) (2)平均维修间隔时间 记k/n(G)系统的寿命为Ts,系统两次维修间的间隔时间为随机变量Y,根据海上任务时间T0可知: (21) 因此,维修间隔时间的分布函数可表示为 (22) 由此可知,维修间隔时间的期望,即平均维修间隔时间为 E(Y)=E(Y|Ts>T0)P(Ts>T0)+ E(Y|Ts≤T0)P(Ts (23) 代入式(4),整理可得 (24) (3)平均维修次数 利用维修平均间隔时间E(Y),可以得到在[0,T0]周期内的平均维修次数为 (25) (4)一次维修的平均备件需求量 利用平均维修次数RT0和备件需求的期望E(N),可以得到在[0,T0]周期内一次维修平均备件需求量为 (26) 由第2节可知,基于事后维修与任务后检修的备件需求模型可以更加准确地反映k/n(G)系统在一次海上任务期内的备件需求。但由于需求模型较复杂,备件需求的概率分布大多用积分形式表示且计算复杂,不便于理解和使用。为此,本节研究随舰备件需求的近似计算方法并给出需求模型的工程解释。 考察某装舰数为1的伽马型部件,其寿命TG服从Gamma分布,TG~Gamma(a,b),概率密度函数为 (27) 分布函数为 (28) 首先,对于装舰数为1的伽马型部件,由文献[17-18]可知,部件与其所配置的备件组成冷储备系统,因此利用Gamma分布的可加性,其备件需求的计算较为容易,满足快速计算的要求。 其次,Gamma分布具有良好的适应性,即当参数取不同值时可以反映不同分布类型,当a为正整数时,f(x)是爱尔兰分布;进一步,当a=1时,f(x)是指数分布。 因此近似计算的基本思路是:若通过适当选取伽马型备件参数a和b的取值,使得其备件需求与基于事后维修和任务后检修的备件需求近似相同,则可以将伽马型备件的备件需求近似作为基于事后维修与任务后检修的备件需求。 由第3.1节基本思路可知,近似计算模型的核心在于如何确定Gamma分布中参数a和b的值,使得伽马型备件需求与真实需求近似一致。本节首先给出近似计算模型,即参数a和b取值的确定方法,然后分析模型的工程解释。 (1)近似计算模型 记k/n(G)系统在事后维修与任务后检修相结合维修模式下的备件需求N的分布列为 P(N=j)=pj,j=0,1,2,… (29) N的期望和方差如式(18)和式(19)所示。 另一方面,对于装舰数为1的伽马型部件,记其备件需求NG的分布列为 (30) NG的期望和方差分别表示为 (31) (32) 显然,式(29)代表k/n(G)系统在事后维修与任务后检修相结合条件下的真实备件需求,可以利用第2节所建模型进行计算,但模型较复杂,不便于理解和使用。 而式(31)表示装舰数为1的伽马型部件在相同任务时间内的备件需求,且计算简单。由文献[18]可知,当j=0,1,2,…时, (33) 式中:G(j)(T0)表示Gamma分布的j重卷积,即 进一步地,由于当分布列相同时,两者的一、二阶矩也必然相同,因此近似计算模型也可表示为 (34) 参数a和b的取值也可由式(34)确定。 (2)模型的工程解释 由式(27)可知,当a=1时,Gamma分布退化为指数分布,参数b即为该指数型备件的失效率。容易计算在[0,T0]内的备件平均需求为 E(NE)=bT0 (35) 而在事后维修与任务后检修相结合的维修模式下,k/n(G)系统在[0,T0]内的备件平均需求E(N)可表示为 (36) 式中:E(NR)为k/n(G)系统在一次维修活动中的平均备件需求量;T0/E(Y)为[0,T0]内的平均维修次数。 由此可见,作为Gamma分布的一个特例,若采用指数型备件进行近似需求计算,则式(34)变为 (37) 观察式(37)可以发现:一方面,参数b反映指数型备件的失效率;另一方面,在事后维修与任务后检修相结合的模式下,由于E(Y)表示维修平均间隔时间,E(NR)表示在一次维修活动中的备件需求量,因此E(NR)/E(Y)恰好反映了k/n(G)系统在一个工作周期内的失效率。 因此,式(37)本质上反映了当采用指数型备件作为近似需求时,核心在于利用E(NR)/E(Y)对指数型备件的失效率进行调整,而E(NR)/E(Y)恰好反映了在事后维修与任务后检修相结合维修模式下的备件失效率。 实际计算发现,采用式(37)进行近似计算具备较高精度,因此作为更一般情形,式(34)表示的近似计算模型是合理的。 需要注意的是,在式(37)中,平均维修间隔时间E(Y)可以利用式(24)直接计算,但第2节给出的E(NR)计算方法较为复杂。为此,接下来给出一种E(NR)的快速估算方法。 根据全概率公式,一次维修的平均备件需求量E(NR)可近似表示为 E(NR)≐E(NR|Ts>T0)P(Ts>T0)+ E(NR|Ts≤T0)P(Ts 式中:E(NR|Ts≤T0)=n-k。 由式(4)可知, (38) (39) 又因为当j=0,1,2,…,n-k+1时, (40) 因此, E(NR|Ts>T0)P(Ts>T0)= (41) 由此可见,E(NR)可表示为 (1-Rs(T0))(n-k) (42) 根据第3.2节的近似计算模型,随舰备件需求近似算法流程如下。 输入舰船任务时间长度T0,k/n(G)系统参数k和n,备件失效率λ。 输出备件需求分布列P(N=j)=pj,平均需求量E(N)。 步骤 1根据式(37)设定伽马型备件参数:即a=1,b=E(NR)/E(Y),其中E(Y)由式(24)确定,E(NR)由式(42)确定。 步骤 2利用式(33)计算伽马型备件需求分布列: P{NG=j}=G(j)(T0)-G(j+1)(T0) 步骤 3将伽马型备件需求分布近似作为备件需求真实分布,即令 P(N=j)=P{NG=j} 步骤 4利用式(18)计算备件需求平均需求量E(N): 为验证近似算法的精度,首先依据工程背景设定备件失效率、任务时间、k/n(G)系统等初始参数。然后,利用第3节近似算法计算备件需求的近似分布及分布特征。接下来,根据第2节建立的备件需求模型计算备件需求的真实分布和分布特征。最后,比较二者的近似程度。具体步骤如下。 步骤 1初始参数设定:依据工程背景,在适当范围内设定参数λ、T0、k和n的取值。 步骤 2伽马型备件参数的确定:利用式(37)计算伽马型备件参数a和b的值。 步骤 3伽马型备件需求分布及特征的计算: 利用式(33)计算该伽马型备件需求的分布,记为 利用式(31)计算该伽马型备件的平均需求量。 步骤 4真实备件需求分布及特征的计算: 利用式(8)、式(16)和式(17),计算备件需求的真实分布,记为 P(N=j)=pj,j=0,1,2,… 利用式(18)计算备件的真实平均需求量。 步骤 5误差比较:定义需求分布的平均误差为 (43) 平均备件需求相对误差为 (44) 例如,取定λ=0.000 1,T0=1 000,k=2,n=4,利用式(37)计算得到a=1,b=3.858 3×10-4。进一步,利用式(31)和式(33)计算得到,伽马型备件需求分布如表1所示,平均需求量为E(NG)=0.385 8。另一方面,利用式(8)、式(16)~式(18)计算得到备件需求真实分布,如表2所示,平均需求量为E(N)=0.380 6。 表1 伽马型备件需求分布 表2 伽马型备件需求真实分布 利用式(43)和式(44)计算得到,需求分布的平均误差为error1=0.006 6,备件平均需求量的相对误差为error2=0.013 0,近似分布误差的整体情况如图4所示。可以看到,对于上述取定的参数,基于Gamma分布的舰船备件需求近似算法具有良好精度。 图4 在取定参数下备件需求分布误差示意图 接下来,取定k=2,n=4,改变参数λ和T0的取值,计算结果如表3所示。 表3 2/4(G)系统在不同参数下的近似结果(k=2,n=4) 观察表3,可以发现如下规律。 (1)当λT0较小(≤1)时,需求分布误差和平均需求误差均较小,这说明近似算法在λT0≤1具有良好的精度。 (2)整体上随着λT0的增大,需求分布误差和平均需求误差均呈现增大的趋势。特别当λT0=2时,误差达到了76.8%,保守起见,当λT0>1时,不应采取近似算法,而使用第2节所建立模型直接计算。 (3)从备件保障实践来看,通过调研发现:实际中λT0超过1的部件项数极少,仅占5%左右,因此近似算法适用于绝大部分备件需求计算问题。 (4)当λT0不变,如表3中λT0=1时,参数λ和T0的变化不影响备件需求。 综上所述,为了进一步验证近似算法的精度,接下来分别针对λT0≤1和参数k、n的典型取值进行计算,结果如表4所示。 表4 k/n(G)系统在不同参数下的计算结果 观察表4可以看到,当λT0≤1时,备件需求的近似计算方法整体上具有较高的精度,满足近似计算的需要。 随着技术水平的进步和管理水平的提高,舰船海上期间的装备维修保障正逐渐转变为事后维修与任务后检修相结合的模式。本文针对这一维修模式特点,通过建立备件需求模型,对常见的k/n(G)系统在一个任务期内的备件需求进行预测,并提出了较简便的近似计算方法,可以为装备备件保障提供参考。但模型仅给出了系统故障不超过1次时的备件需求,虽适用于95%以上的备件需求预测问题,但采用需求模型对备件需求直接计算仍较复杂,接下来还需进一步对需求分布进行完善。2.2 n -k+1≤N≤2(n -k)+1时的概率分布


2.3 N>2(n -k)+1时的概率分布
2.4 需求分布的特征
3 舰船备件需求的近似计算方法
3.1 基本思路
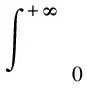
3.2 近似计算模型及其工程解释

3.3 算法设计
4 算法验证





5 结 论
