镧系裂变产物(La、Ce、Pr和Nd)在α-U表面偏析行为的第一原理研究

2021-07-27曹金利王志超豆艳坤贺新福

原子能科学技术 2021年7期

曹金利，王志超，王瑾，豆艳坤，贺新福,*，杨文

(1.中国原子能科学研究院反应堆工程技术研究所，北京 102413；2.北京科技大学材料科学与工程学院，北京 100083)

金属燃料具有热导高、裂变原子密度高、增殖比高(金属燃料为1.24，氧化物燃料为1.05)、多普勒系数小、制造成本相对较低、后处理流程简单等优点[1-4]，是快堆未来燃料的必然选择，也是先进燃料循环技术的发展方向。采用U-20Pu-10Zr为燃料、HT-9为包壳材料的Mark-V燃料棒设计，其最高燃耗可达18.40%[5]。U-10Zr及U-20Pu-10Zr金属燃料是快堆实现高增殖嬗变的候选燃料之一。

镧系裂变产物引起的燃料肿胀以及对包壳产生的腐蚀是制约UZr及UPuZr金属燃料的重要问题[6-7]。在快堆服役过程中，除高裂变产率的惰性裂变气体外，还有大量的固态裂变产物，镧系元素主要是镧(La)、铈(Ce)、镨(Pr)、钕(Nd)等。随着燃耗的升高，燃料内部会积累大量的裂变产物。实验表明，镧系裂变产物在燃料中的扩散速度非常快，被称为“类液体扩散”。对于该现象，固体扩散不能解释镧系裂变产物快速扩散行为[8]，研究者提出了几种扩散机理，其中广为接受的是表面扩散和借助于裂变气体通道中充斥的液态钠(Na)和铯(Cs)的液态扩散[9-10]。对于快速扩散机理，目前还存在一些争议，但这两种机理的前提是镧系裂变产物都会偏析到裂变气体形成的释放通道。而且早在1990年，已有实验[11]观察到镧系裂变产物会偏析到裂变气泡及气体通道。文献[12-13]模拟研究了镧系裂变产物在液态钠和铯中的分布及扩散行为，但对于镧系裂变产物在裂变气体通道的偏析及扩散行为尚未见报道。

UZr金属燃料在实际服役过程中，Zr元素重新分布导致沿径向出现不同的相区：燃料芯部的高温γ相、外部的低温α相。α相位于金属燃料外部，其体积分数约占UZr燃料块的70%。尽管γ相在高温实验中稳定，但先前的研究和计算[14]均表明，它在第一原理计算中的结构是不稳定的，且在添加1个点缺陷空位后会引起结构的自发转变。在第一原理计算中，γ相的Zener剪切常数为负[15-16]。这可能与0 K时γ相的不稳定性有关，本文主要关注裂变产物在低温α-U中的行为。

本文拟采用自由表面模拟裂变气体通道，通过第一原理方法模拟镧系裂变产物在低温α-U表面的偏析行为，计算中考虑6种不同表面((100)、(112)、(001)、(021)、(110)、(010))，分析镧系裂变产物La、Ce、Pr和Nd的偏析行为。

1 计算方法与模型

本文采用基于密度泛函理论(DFT)和平面波赝势的VASP软件[17-19]进行计算。计算中使用投影缀加平面波的方法描述电子-离子实的相互作用[20-21]，用广义梯度近似(GGA)下的PBE泛函描述电子与电子间的交换关联作用[22]。平面波基组的截断能选取350 eV，大于研究体系中赝势的默认值，总能量收敛优于1×10-5eV。

锕系元素U的5f电子具有很强的关联作用，电子云扩展方向的复杂性及其巡游性导致传统的局域密度近似(LDA)或广义密度近似(GGA)泛函很难准确描述其轨道的多体效应。对于UO2或过渡金属氧化物，考虑到带隙及原子的库仑相互作用对轨道的依赖性，添加Hubbard U(与自旋相关的有效库仑势)对标准DFT计算的校正效果较好，通常称为DFT+U方法。但对于金属铀及铀锆合金体系，采用经验性Hubbard U校正的效果并不是很好[23-24]，目前普遍采用的仍是标准DFT方法[14,25-28]。最近的模拟计算[25-26]中，不考虑库仑相互作用的计算结果显示，α-U中自扩散的激活能与实验结果相符，为0.10 eV。对于镧系元素，其在液态钠和铯中的溶解和扩散计算[12-13,29]也采用标准的DFT。更重要是，DFT+U近似将电子局限在特定轨道上，会带来亚稳态的出现[30-32]，尤其是对于含有面缺陷的体系。因此，本文的计算均采用标准DFT方法。

计算中6种表面的层数均设置为10层，使用周期性边界条件，x-O-y面上采用2×2超胞，每层含8个原子。在晶面的法线方向上加入1.5 nm的真空区域，以最大程度地降低表面之间的相互作用。对于6种表面结构，其K点网格分别设置为：(3×3×2)、(3×4×1)、(5×3×1)、(6×3×1)、(4×5×1)、(5×3×1)，不同K点的选取主要与各表面的基矢长度相关。

1.1 α-U晶格结构

α-U的晶格结构示于图1。由图1可见，α-U具有正交结构，其晶胞含有4个原子，原子坐标分别为(0，0，0)、(0.50,0.50,0.00)、(0.50,0.30,0.50)和(0.00,0.80,0.50)。密排面为准(010)面，该晶面并不是常见的规整晶面，晶面上原子有一定的上下浮动，称为“褶皱面”。采用图1所示的晶胞，用17×11×11的K点网格划分布里渊区，获得晶格常数：a=0.280 nm、b=0.584 nm、c=0.490 nm，与Huang等[26]使用GGA-PW91计算和Taylor[33]的自旋轨道耦合计算结果相一致。Söderlind[34]采用全电势计算的晶格常数为a=0.285 nm、b=0.582 nm、c=0.499 nm。Barrett等[35]在40 K下获得的实验值为a=0.284 nm、b=0.587 nm、c=0. 494 nm。与本文计算值的相对误差为2%，在可接受的误差范围内。

图1 α-U 的晶胞示意图Fig.1 Structure of α-U

1.2 表面模型构建

(100)、(112)、(001)、(021)、(110)、(010) 6种常见模拟裂变产物的表面模型如图2所示。图2中，A代表直接暴露在真空中的表面，B代表次表面层，依次类推，最中间的2层E代表U的体相晶格结构及化学环境，图2b与图2d～f中，由于晶面不平整，同一层的原子分为2类，如表面原子有A1和A2 两种类型，次表面有B1和B2 两种。因此下文计算时，对于(112)、 (021)、(110)和(010)表面，层间距计算时有B1-A1和B2-A2两种，计算结果中表示为“表面X-1”和“表面X-2”。 6种表面模型优化后的层间距示于图3，其中虚线为完美晶格的层间距。由图3可见，6种表面中，(100)表面的层间距最小，为0.140 nm。(100)表面层数的收敛性测试结果列于表1。从表1可看出，表面形成能随着层数的增加基本不变，约为2.04 J/m2。层数的收敛性测试结果表明，10层平板模型的厚度对于模拟α-U表面是足够的。

图3中，靠近表面处的原子其晶面间距明显减小，这主要是由于表面原子的键断开，产生悬键，引起表面塌陷。从表面层到次表面层，远离表面的过程中，其层间距显示出向体相层间距的振荡衰减。(100)、(112)和(110)表面的振幅稍大，随着层厚的增加，层间距的振荡依然存在。对于过渡金属或铀体系[28,36]，1 nm 或8层slab模型足以用于模拟表面或表面偏析。表2和图3的结果表明，超胞的中心部分可代表体相环境的形成，计算中采用的表面模型是合理的。

a——(100)表面；b——(112)表面；c——(001)表面；d——(021)表面；e——(110)表面；f——(010)表面；A～E为原子层图2 6种自由表面模型Fig.2 Six free surface models

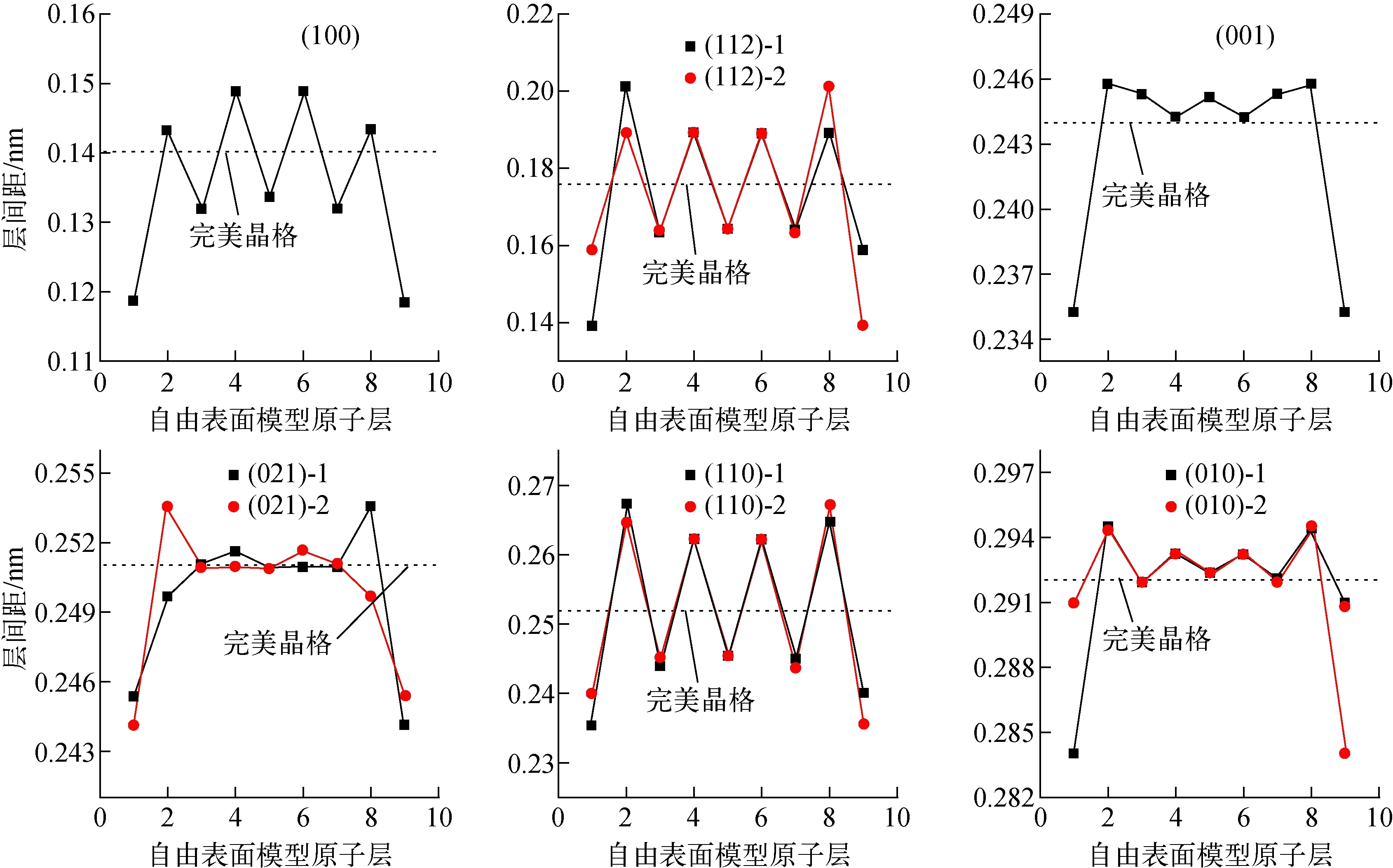
图3 6种表面模型优化后的层间距Fig.3 Interlayer distances of six free surfaces under optimization.

表1 (100)表面形成能随模型原子层数变化的收敛性测试结果Table 1 Convergence test result of (100) surface free formation energy with number of layer of model

2 结果与分析

2.1 自由表面形成能

(1)

式中：EFS为包含自由表面的超胞的总能；Eperfect为完美α-U超胞的总能；S为自由表面的面积。图2所示自由表面模型中包含2个等效的自由表面，因此式(2)分母是相应面积S的2倍。

6种自由表面的层间距及形成能列于表2。其中(110)表面的形成能最低，为1.75 J/m2；(112)、(021)和(001)表面的形成能次之，分别为1.81、1.83、1.83 J/m2；(010)和(100)表面的形成能最高，分别为1.96 J/m2和2.04 J/m2。

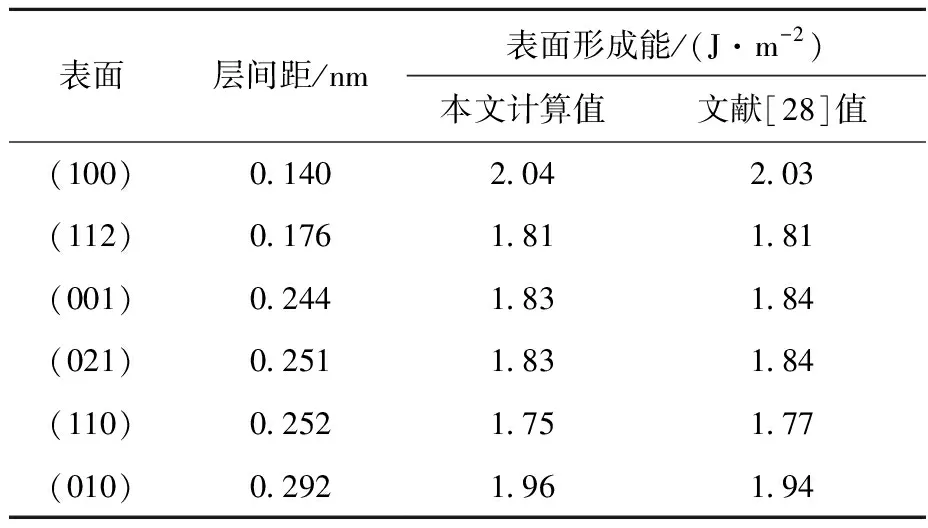
表2 6种表面的层间距及形成能Table 2 Free formation energy and interlayer distance of six free surfaces

本文计算结果和文献[28]结果一致。

2.2 镧系裂变产物在表面的偏析

裂变产物X(X = La，Ce，Pr和Nd)的偏析能(Eseg)可定义为：

(2)

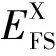
如图2所示，裂变产物X原子分别被置于表面附近的5个不同的取代位置，因此从表面位置A逐渐偏离表面到位置E来计算镧系元素在表面的偏析行为。位置E可代表体相环境，作为式(2)的参考态。在计算中，X仅替代每层中任意一个铀原子，偏析原子密度为12.50%。

镧系裂变产物La、Ce、Pr和Nd在6种自由表面的偏析能示于图4，从左到右可看作是镧系元素从表面向体相的偏析能变化。从图4可看出，4种裂变产物元素在表面层A(A1或A2)的偏析能的绝对值最高，其偏析能力最强。

图4 裂变产物元素La、Ce、Pr、Nd在表面的偏析能Fig.4 Segregation energy of La, Ce, Pr and Nd on free surface

对于次表面，除(100)表面外，4种裂变产物元素的偏析能有较小的正值，表明有微弱的排斥。对于次次表面C层和离表面更远的D层，其偏析能都非常小，接近于0 eV。这也说明，在原子尺度上表面短程作用只能影响2～3层，这与之前体心立方金属中铁的表面偏析行为[37]类似。以上结果表明，在6种自由表面处，4种镧系裂变产物都表现出明显的偏析效应。

同时，分析图4可得：La的偏析驱动力最大，偏析能为-1.84～-2.53 eV；其次是Ce，偏析能为-0.71～-1.11 eV；然后是Pr，偏析能为-0.45～-0.79 eV；最小的是Nd，其偏析能较Pr的偏析驱动力略小，为-0.40～-0.65 eV。Ce的偏析能约为La的1/2。可见，对于同一种表面，其偏析驱动力顺序为：La>Ce>Pr>Nd。在不考虑磁性影响体系时，表面偏析的驱动力很大程度上来源于体积效应。本文所考察的4种镧系元素的离子半径(La，0.207 nm；Ce，0.204 nm；Pr，0.203 nm；Nd，0.201 nm)均大于金属铀的离子半径(0.196 nm)。4种镧系裂变产物元素在金属铀体相中会受到挤压，当其位于表面处时，会释放一定的畸变压应力，缓解嵌入引起的畸变能。因此，镧系元素原子尺寸随原子序数的增加而减小，表现出一定的镧系收缩现象，其在铀金属表面的偏析能力也逐渐减小。

同一镧系元素在不同自由表面的偏析能如图5所示，沿横坐标从左到右晶面层间距依次增大，(100)表面为层间距最小的稀疏排布表面，(010)表面为层间距最大的密排面。纵坐标为裂变产物在表面的最大偏析能，即位于表面原子层A的结果。从图5可看出，最左边的偏析驱动力最大，即杂质在稀疏排布表面偏析驱动力较大，在密排面的偏析驱动力小。这与过渡金属体心立方金属铁(Fe)中的规律一致，过渡金属杂质在Fe(110)密排面偏析驱动力较其他面的低，较(100)表面的偏析能约小1/2。表面偏析驱动力的降低主要是由于杂质和溶剂原子断开第1近邻键数量减小。Ruban等[37]根据Friedel模型，基于28×28组计算数据，针于过渡金属建立了一个表面偏析模型，与表面属性相关的表达式可表示为：

(3)

其中，zs和zb分别为表面和体相中的配位数。

采用式(3)可评估同种元素在不同表面偏析能力的变化。如图1所示，α-U具有正交结构，考虑其“名义”上的第1近邻(原子间距<0.330 nm，正交结构的对称性较低，其第1近邻有2个，间距为0.270 nm；第2近邻有2个，间距为0.280 nm；第3近邻有4个，间距为0.324 nm)，体相中的配位数为8，即zb=8。对于(010)密排面，其表面断开2个键，表面的配位数zs=6；对于层间距最小的(100)表面，其表面断开4个键，表面的配位数zs=4。利用式(3)可估算出元素在(100)表面的偏析驱动力为(010)表面的2.19倍。4种元素不同自由表面处的偏析能变化均较平缓，整体上，其偏析能随面间距的增加逐渐减小。La、Ce、Pr和Nd的(100)与(010)表面偏析能的比值分别为1.3、1.22、1.13、1.06，明显低于模型计算结果(2.19)。这可能与杂质的原子半径和晶格结构有关。

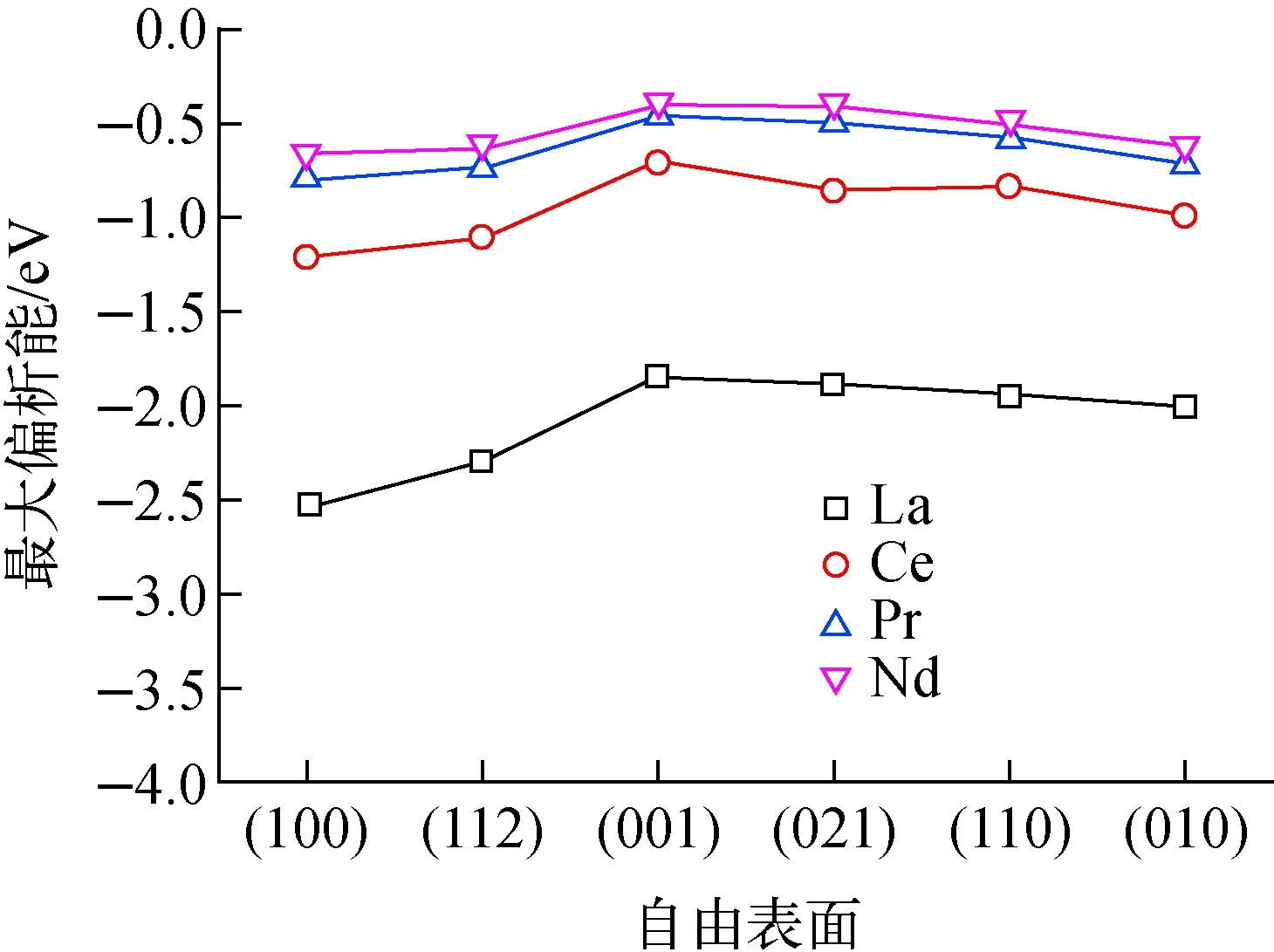
图5 裂变产物La、Ce、Pr、Nd在不同表面上的偏析能Fig.5 Segregation energy of fission products La, Ce, Pr and Nd for various free surfaces

2.3 镧系裂变产物在表面偏析的热力学行为

使用Mc-Lean方程可在热力学上估算尾闾包括表面附近杂质的占据概率[38]：

(4)

其中：Eseg为自由表面附近杂质的偏析能；Cbulk为体相中杂质的浓度；kB为玻尔兹曼常数；T为时效温度。

本文镧系元素的偏析能Eseg采用6种表面的数学平均值，La、Ce、Pr和Nd的偏析能分别为-2.08、-0.95、-0.62、-0.54 eV。在钠冷快堆中，燃料外部温度范围为773～973 K。在快堆中，裂变产物的产率(原子浓度)仅为(2～10)×10-6，从燃料芯部沿温度梯度向外扩散，在α-U燃料中浓度偏高。在典型的模拟燃料服役行为的MOOES/和BISON程序中[39]，裂变产物源的原子浓度高达10-2。因此，本文研究两种杂质原子浓度：10-4、10-2。不同温度(773 K和973 K)、不同体相浓度(原子浓度10-4和10-2)下，裂变产物元素在表面的占据概率示于图6。从图6可看出，拥有强偏析能的裂变产物元素在更低温度和更高的体相浓度下，在表面处的占据概率更高。在773和973 K温度下，La和Ce在表面的占据概率接近于1；对于Pr和Nd，973 K温度和10-4原子浓度下，其在表面的占据概率仍接近于0.10。因此，采用第一原理方法分析低温、高浓度镧系裂变产物元素的偏析行为仍是有意义的，且4种裂变产物La、Ce、Pr和Nd在热力学上都会偏析到表面。

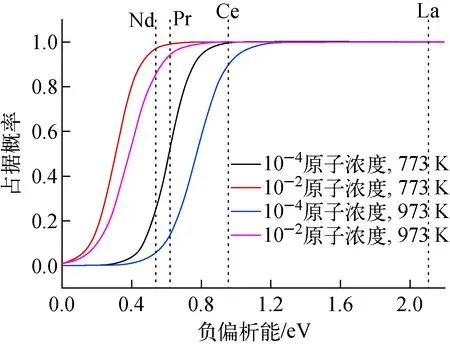
图6 不同温度和体积浓度下镧系裂变产物在表面的占据概率随偏析能的变化Fig.6 Probability of Ln fission product near free surface as a function of segregation energy at different temperatures and bulk concentrations