基于AHP-TOPSIS模型山岭隧道施工安全评价研究

2021-07-27兰小波武柏毅

工程与建设 2021年2期

卢蒙，兰小波，武柏毅

(中铁隧道局集团建设有限公司，广西南宁 530003)

0 引言

随着施工技术的不断提升,目前在道路修建中,人们越来越重视道路的运营效率及环境保护。新技术、新设备、新材料的加入使得在复杂地形环境中施工成为可能,从而大大缩短道路里程,使人们出行更加快速、便捷,同时最低限度地破坏沿线环境。因此,道路工程要求路面越来越宽,穿越的地质也越来越复杂,施工重难点则主要体现在山体隧道开挖及桥梁架设阶段。山体隧道施工难度较大,存在着极大的施工风险,因此,为了提高现场施工安全管理水平,有必要对该类施工项目进行总体的安全评价。

层次分析法(AHP)作为一种多层次指标定量评价方法在建筑施工中运用较为广泛,廖斌[1]采用AHP方法分析了建筑施工中5M体系各因素指标的权重,鲍学英等[2]采用AHP方法评价了地铁施工安全等级,刘辉等[3-5]采用相同方法分析了隧道工程中各安全指标的权重,评价结果与现场情况较为一致。逼近理想解排序法(TOPSIS)是一种有限方案多属性的决策方法,能够对多指标的相对优劣做出排序[6],但不适用与多层次指标。采用AHP法来确定各目标层的权重可以弥补TOPSIS法存在的不足,贾宝山[7]等将AHP和TOPSIS法相结合,评价了矿井安全等级找出了存在的安全隐患,王纪洋等[8]等采用AHP-TOPSIS方法对化工工艺的安全等级进行了安全评价,杨立成等[9]用相同方法评价了医院感染管理质量,从以上评价结果来看,AHP耦合TOPSIS评价方法更为客观,评价结果与现场情况较为一致。综上笔者将AHP-TOPSIS应用到目前在建隧道工程项目的安全评价中,以提高施工过程中的安全管理水平。

1 AHP-TOPSIS评价模型

1.1 AHP法确定指标权重

层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构,然后用求解判断矩阵特征向量的办法,求得每一层次的各元素对上一层次某元素的优先权重,最后再加权和的方法递阶归并各备择方案对总目标的最终权重[10]。AHP法确定指标权重步骤如下:

1.1.1 建立层次结构模型

根据对问题中各因素之间的关联关系,将具有共同特征的因素归纳成组,并根据相同的特征关系逐级分层,最高层为目标层,最底层为具体方案层,中间层为准则层。

1.1.2 构造判断矩阵

判断矩阵表示针对上一层中某元素,本层次中与其有关元素之间相对重要度的比较,主要采用1-9标度法计算指标重要度,构成判断矩阵S。

(1)

式中:Sij为指标重要度比值,表示第i个指标重要度与第j个指标重要度之比。

1.1.3 一致性检验

由于判断矩阵主要是由专家主观评判结果构成,难免会出现误差,因此,为了使判断矩阵更加合理,需要对矩阵进行一致性检验,采用Saaty提出的一致性方法[11],计算公式如下。

(2)

式中:CI为一致性指标;RI为平均随机一致性指标;λmax为判断矩阵S的最大特征值;m为判断矩阵的阶数;CR为判断矩阵的一致性比例,一般认为当CR<0.1时判断矩阵具有可以接受的一致性,否则就需要对判断矩阵进行修正。

1.1.4 指标权重的计算

一般采用几何平均法计算指标权重,几何平均法是将判断矩阵各个行向量进行几何平均,所得到的行向量即为权重向量,计算公式如下:

(3)

1.2 TOPSIS评价模型

TOPSIS法的基本思路是定义决策问题的正理想解与负理想解,各方案优劣按与理想解的距离排序,距正理想解最近而距负理想解最远为最优方案,反之则为最劣方案[6]。TOPSIS法评价步骤如下。

1.2.1 建立多属性评判矩阵

根据问题包含的方案及其对应的方案属性建立评判矩阵A。

(4)

式中：xij表示第i个方案的第j个属性评价指标。

1.2.2 决策指标的标准化

评价指标分为效益型和成本型,效益型指标数值越大越好,而成本性指标越小越好,因此需要先对评价指标进行同极化处理,一般选择对成本性指标取倒数。由于不同指标的量纲不同且变化范围大小不同,需要对评价指标进行无量纲化处理,最后得到标准化决策矩阵A′,计算过程如下。

(5)

(6)

(7)

式中:xij*为同极化处理后的指标值；zij为无量纲化指标值。

1.2.3 建立加权标准化决策矩阵

将标准化决策矩阵A′的每一列与其对应的指标层中各指标的总排序权重作乘,得到加权标准化决策H。

(8)

1.2.4 样本贴近度计算

(1)正理想解与负理想解计算:

(9)

式中:z+、z-分别为正负理想解。

(2)评价指标到正负理想解的欧式距离计算:

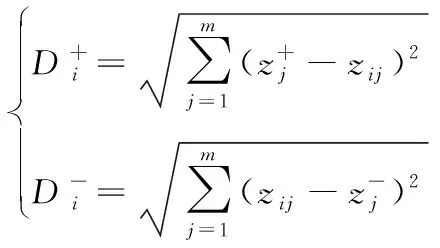
(10)

式中：Di+、Di-分别为评价到正负理想解的欧式距离。

(3)贴近度计算:

(11)

式中:Li为各方案与最优方案的贴近度。其中Li在0与1之间取值,值越接近1表示该指标越接近最优。

1.3 AHP-TOPSIS模型

根据样本贴近度的计算结果构造判断矩阵,结合各指标层的权重分配可以得到样本的综合评价向量F。

F=ω×L

(12)

式中：ω为指标准则层权重;L为贴近度判断矩阵。

2 南马鞍隧道施工安全评价

2.1 工程概况

南马鞍隧道处于新晋高速公路块村营至营盘段第15标段，隧址位于太行山脉南马鞍山岭，地形起伏较大，隧道穿过该山岭主峰，高程1 497.8 m。隧洞进出口为冲沟，植被发育，局部发育陡崖，岩体多暴露，地貌单元属于中山地貌。隧道区内岩性以寒武系页岩为主，强风化层节理裂隙较发育，地下水类型属基岩构造裂隙水，补给来源主要是大气降水，受山体影响，在局部地段会形成含水体并出现小规模涌水现象。隧洞围岩为中、微风化灰岩，属坚硬岩，围岩级别为Ⅲ、Ⅳ级呈块状结构，长时间暴露易出现局部坍塌。

2.2 施工安全评价指标体系

根据系统工程事故致因相关理论,从人、机、环、管四个方面对山岭隧道施工安全状况进行综合分析,结合AHP方法理论建立山岭隧道施工安全状态三级评价指标体系,体系由目标层(O)指标、准则层(S)指标及底层(B)指标构成,各层指标相关性如图1所示。

图1 隧道施工安全状态评价指标

2.3 风险等级划分标准

根据《铁路隧道风险评估与管理暂行规定》[12]中对风险可接受准则的规定，将隧道施工安全状态分为Ⅰ级(低度风险可忽略)、Ⅱ级(中度风险可接受)、Ⅲ级(高度风险不期望)、Ⅳ级(极高风险不可接受)四个等级，安全状态等级评价标准见表1。

表1 隧道施工安全状态等级评价标准

2.4 AHP法计算指标权重

结合专家及现场技术人员打分结果,根据事故致因相关理论构造如下判断矩阵,准则层S1、人的因素S2、物的因素S3、环境因素S4、管理因素S5:

利用MATLAB求得各矩阵最大特征值λmax依次为4、4、7、4、5,根据公式(2)求得各矩阵的CR值均为0<0.1,因此各矩阵一致性满足要求。

根据公式(3)求得各矩阵对应的指标权重向量依次为ω1=(0.431,0.143,0.143,0.283),ω2=(0.429,0.143,0.214,0.214),ω3=(0.051,0.205,0.154,0.256,0.027,0.051,0.256),ω4=(0.067,0.333,0.267,0.333),ω5=(0.077,0.231,0.154,0.231,0.307)。由此可得底层指标总权重值,见表2。

表2 底层指标总权重

2.5 TOPSIS法指标评判

(1)人的因素。根据表1中指标数据,建立多属性初始评判矩阵A,其中每列数据表示底层指标安全等级量化值,最后一行为实例样本值。

由表1中指标值的变化趋势可知,B2为成本性指标,进行矩阵标准化首先要按公式(5)计算处理,然后根据式(6)和式(8)计算,得到加权标准化决策矩阵H1。

根据式(9)得到基于人的因素的正、负理想解如下:

Z+=[0.125,0.055,0.068,0.076]T

Z-=[0.031,0.014,0.021,0.015]T

根据式(10)计算得到各因素指标到正、负理想解的欧氏距离:

D+=[0,0.085,0.128,0.07]T

D-=[0.128,0.056,0,0.077]T

根据式(11)计算得到各因素指标与正理想解的贴近度:

L=[1,0.397,0,0.917]T

(2)物的因素。同理可得物的因素加权标准化决策矩阵H2:

其对应的正、负理想解分别为:

Z+=[0.0038,0.0155,0.0116,0.0199,0.0021,0.0037,0.0199]T

Z-=[0.0032,0.0133,0.0103,0.0177,0.0019,0.0033,0.0177]T

其对应的欧氏距离分别为:

D+=[0.005,0.0061,0.0074,0.0062]T

D-=[0.0038,0.0019,0,0.0025]T

其各指标与正理想解的贴近度为:

L=[0.432,0.238,0,0.287]T

(3)环境因素。同理可得环境因素加权标准化决策矩阵H3:

其对应的正、负理想解分别为:

Z+=[0.0082,0.0309,0.0311,0.0325]T

Z-=[0.0027,0.0017,0.0026,0.0058]T

其对应的欧氏距离分别为:

D+=[0,0.019,0.044,0.049]T

D-=[0.049,0.031,0.008,0]T

其各指标与正理想解的贴近度为:

L=[1,0.620,0.154,0]T

(4)管理因素。同理可得管理因素加权标准化决策矩阵H4:

其对应的正、负理想解分别为:

Z+=[0.0129,0.0389,0.0253,0.0395,0.0533]T

Z-=[0.0086,0.0259,0.0168,0.0263,0.0356]T

其对应的欧氏距离分别为:

D+=[0,0.0137,0.0273,0.0193]T

D-=[0.0273,0.0136,0,0.0105]T

其各指标与正理想解的贴近度为:

L=[1,0.498,0,0.352]T

2.6 安全状态综合评价

根据2.5节计算结果得到各因素指标与正理想解的贴近度矩阵M,根据2.4节由AHP法计算得到准则层指标权重矩阵ω1:

由式(12)计算可得综合评价向量F:

F=ω1×M=[0.919,0.435,0.022,0.536]

由以上计算结果可得山岭隧道施工不同安全级别的量化分级标准，见表3。

表3 安全等级标准

样本值为0.536,由表3可知,该隧道施工安全等级为Ⅱ级,符合现场实际情况,说明该评价方法合理正确。

3 评价结果分析

由TOPSIS评价原理可知,样本综合数值越小表示其危险性越大。对于准则层元素,从各因素指标与正理想解的贴近度矩阵M可知,环境因素对应指标值为0,说明环境是影响施工安全的重要因素,其次是物的因素,对应指标值为0.287,然后是管理因素,对应指标值为0.352,人的因素为0.917相对较安全。由环境因素加权标准化决策矩阵H3可知:地质危险等级(0.0027),噪声等级(0.0017),平均粉尘最大浓度(0.0026),平均温度(0.0058),因此,噪声对施工安全影响最大,其次是粉尘浓度和地质风险因素。由设备因素加权标准化决策矩阵H3可知,支护设备(0.0021)对施工安全影响最大,其次是爆破器材(0.0038)和防灭火设备(0.0035),指标值均明显小于其余因素指标值。

根据以上分析可知,该隧道工程施工过程应加强对作业环境及作业设备的管控。考虑施工过程的安全性,可以采取相应措施降低作业面噪声、粉尘对人员的危害以及对作业过程的影响;加强地质观测,对地质风险较大区域制定专项施工方案;增加对支护设备、爆破设备及防灭火设备的检修频率,结合施工成本可以提前考虑购置新设备进场。