波形钢腹板预应力混凝土连续梁桥参数敏感性分析
2021-07-27杜岩松宋涛王保群
杜岩松,宋涛,王保群
山东交通学院 交通土建工程学院,山东 济南 250357
0 引言
波形钢腹板广泛应用于我国各类桥梁结构中,波形钢腹板预应力混凝土连续梁桥将常规混凝土腹板替换为波形钢腹板,常规混凝土腹板抗弯、抗剪性能优越,预应力损失较小[1-6]。波形钢腹板的手风琴效应减少了混凝土收缩徐变,解决了传统预应力混凝土箱梁桥腹板开裂的问题[7-9],对实现桥梁的经济性、美观性及节能省材有重大意义[10-11]。应用波形钢腹板能使主梁质量减小30%左右,波形钢腹板中附带的加筋板很大程度上解决了跨中下挠问题[12]。
分析桥梁参数敏感性是定量分析某些不稳定因素对桥梁结构的影响程度,我国大跨径波形钢腹板梁桥数量不多,这方面的研究比常规梁桥少。影响波形钢腹板预应力混凝土大跨径连续梁桥的因素较多,本文借助有限元分析手段,综合分析主梁质量、主梁混凝土弹性模量、预应力钢筋损失和混凝土收缩徐变等参数对桥梁结构性能的影响程度,即参数敏感性,确定主要、次要参数,以期为现场施工控制提供可靠的技术指导,保证成桥后的线形平顺和结构的安全稳定。
1 工程概况
减河大桥是京台高速公路德州(鲁冀界)至齐河段改扩建工程,桥梁右幅跨径为92 m+142 m+86 m(左幅跨径为86 m+142 m+86 m),主桥上部结构为波形钢腹板变截面预应力混凝土连续梁桥,分幅设置,单幅桥宽20.5 m,桥梁单向坡度为2%,单箱双室截面。该桥主桥桥型布置见图1、2(图1中单位为cm;图2中H为变截面箱梁横断面中心高度,cm)。

图1 减河大桥桥型布置示意图
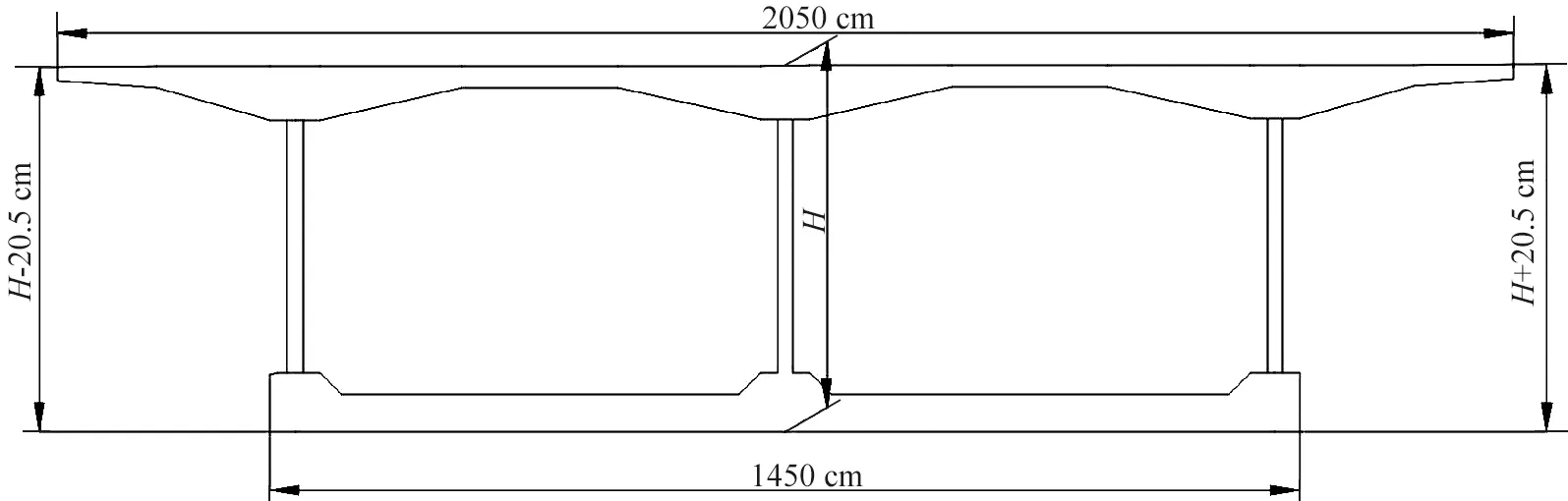
图2 减河大桥箱梁典型断面示意图
2 结构计算模型
采用Midas Civil软件建立减河主梁大桥主梁右幅有限元模型,如图3所示。

图3 减河大桥主梁右幅有限元模型
主梁采用组合单元模拟,对该桥进行结构分析。该桥右幅模型中包括105个节点,90个梁单元。全桥共56根纵向预应力钢筋,其中51根体内预应力钢筋,5根体外预应力钢筋。主梁0#块位置的临时支撑采用固结、刚性连接。主梁所受荷载包括主梁自重、预应力、横隔板自重、挂篮、边跨压重、二期恒载。
建模时将横隔板自重等效成节点荷载考虑。该桥采用悬臂现浇方式,将挂篮自重等效成节点荷载施加。二期铺装采用梁单元荷载模拟[13-16]。
3 结构参数敏感性分析
通过定量分析减河大桥结构,将主梁质量、主梁的混凝土弹性模量、预应力损失以及混凝土的收缩徐变作为主控参数,通过有限元分析软件计算其对主梁顶板、底板应力和主梁挠度的影响程度,最终确定参数敏感性。
3.1 主梁质量
在施工过程中,多方面原因导致主梁质量发生变化,如混凝土弹性模量变化,实际施工时施加混凝土过多,振捣器局部老化或工人水平局限导致混凝土局部密实度不同,温度变化、阳光直射及雨淋等环境原因导致模板变形,或尺寸与原尺寸相差较大等[17-18]。本文分析主梁质量分别增加5%、10%时对主梁顶板、底板应力和主梁挠度的不同影响,结果见图4、5。
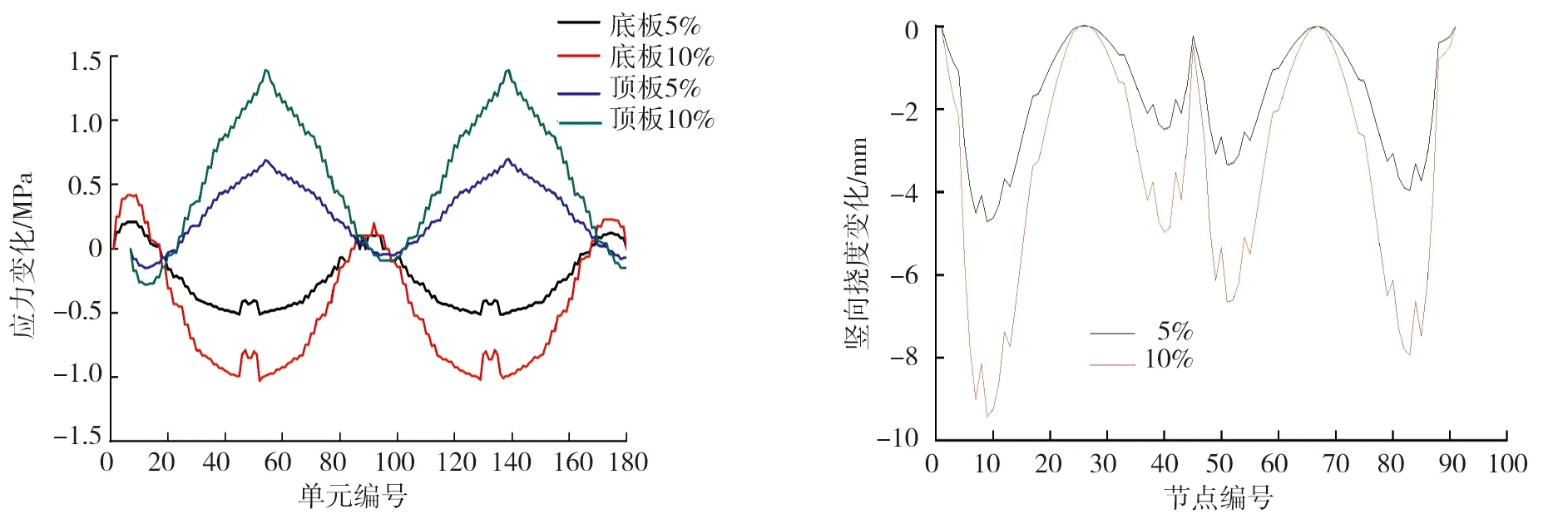
图4 主梁质量增加时梁单元顶板、底板应力变化 图5 主梁质量增加时主梁竖向挠度变化曲线
由图4、5可知:主梁质量在一定范围内小幅变化对主梁挠度和应力的影响较大。主梁质量增加时,0#块位置底板应力变化较大,边跨合龙处顶板应力变化较大,边跨合龙、中跨合龙处主梁竖向挠度变化较大。因施工中存在一定误差,实际的挠度变化比理论变化大,所以主梁质量增加对挠度变化的影响更大。
因此,边跨合龙、0#块位置和中跨合龙处为应力和挠度主要变化区域,应对其着重监测,以保证成桥后的结构安全和线形平顺。
3.2 主梁混凝土弹性模量
主梁混凝土理论弹性模量与施工时的实际弹性模量不同,结构刚度与预期不同。考虑混凝土弹性模量分别增加5%、10%两种情况,对结构的影响结果见图6、7。

图6 弹性模量增加时顶板、底板应力变化曲线 图7 弹性模量增加时主梁竖向挠度变化曲线
由图6、7可知:混凝土弹性模量小幅变化对结构影响不明显。混凝土弹性模量增加时,应力变化范围较小。混凝土弹性模量不是影响主梁应力变化的主要原因。混凝土弹性模量增加5%和10%,主梁最大挠度变化分别为2.63、5.03 mm,弹性模量的增大造成竖向挠度的增大。混凝土弹性模量增大时,边跨合龙处挠度变化较大。
因此,若混凝土弹性模量由5%递增至10%,竖向挠度变化约增大1倍,可将混凝土弹性模量作为次要参数考虑[19]。
3.3 预应力损失
预应力筋与管道壁摩擦、锚具变形、钢筋与台座间的温差、混凝土弹性压缩和钢筋松弛均引起预应力损失[20-22],考虑预应力分别减少5%、10%两种情况,对结构影响结果见图8、9。
由图8、9可知:预应力在一定范围内的小幅损失对主梁应力和挠度影响较大。预应力减少时,边跨合龙、中跨合龙处主梁底板应力变化较大,0#块位置主梁顶板应力变化较大,中跨合龙处主梁挠度变化较明显。
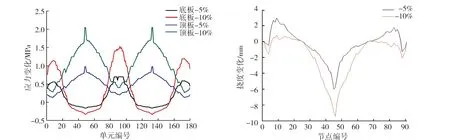
图8 预应力损失减少时底板、顶板应力变化曲线 图9 预应力损失减少时主梁竖向挠度变化曲线
因此,边跨合龙处、中跨合龙处和0#块位置为主要影响区域[23-24]。预应力损失应作为施工过程中的关键控制参数,加强监控。
3.4 混凝土的收缩徐变
现浇混凝土若没有达到应有的养护龄期就投入使用,混凝土收缩徐变将非常明显,影响桥梁结构的应力和变形[25]。分析成桥1、3、5、10 a时的收缩徐变,对结构影响结果见图10、11。
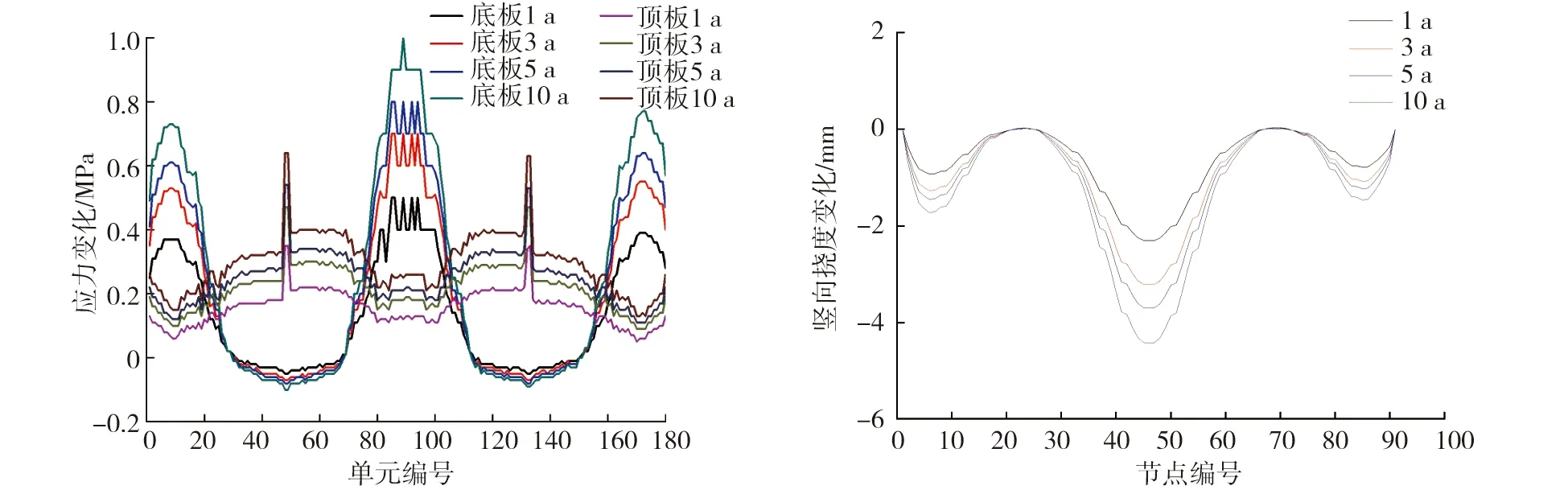
图10 混凝土收缩徐变不同时顶板、底板应力变化曲线 图11 混凝土收缩徐变不同时主梁竖向挠度变化曲线
由图10、11可知:混凝土收缩徐变随着成桥年限增长,对主梁结构的影响程度增大,符合混凝土徐变原理。随着成桥年限增长,边跨合龙、中跨合龙处底板应力变化较大,0#块位置底板应力变化较大,主梁挠度变化增大。
成桥10 a,底板最大和最小应力变化分别为1.00、-0.10 MPa。边跨合龙处、中跨合龙处和0#块位置应力和挠度变化较大。在实际施工时应将混凝土收缩徐变作为主要控制参数,着重对边跨合龙处、中跨合龙处和0#块3个位置进行监控。
4 结论
1)主梁质量、预应力损失和混凝土收缩徐变对桥梁的应力、挠度影响均较大,将其作为主要控制参数。主梁混凝土弹性模量变化对结构影响较小,可作为次要控制参数。边跨合龙处、中跨合龙处和0#块位置各参数变化较大,在实际施工时应对上述位置加强施工监控,保证桥梁成型后线形平顺。
2)现场施工时注意浇筑的混凝土体积的变化,确保模板位置正确及尺寸合适,完成浇筑后严格遵从混凝土养护时间,减小收缩徐变对桥梁的影响。预应力损失对桥梁结构短期内影响最为明显,须严格控制预应力损失,确保成桥后结构安全,线形平顺。
3)本文仅分析各项参数变化对桥梁主体的影响,没有分析参数变化对局部构件的影响,例如各参数变化对波形钢腹板剪应力的影响程度。可进一步分析波形钢腹板混凝土连续梁桥局部附件其他力学性能的变化,获得更准确参考数据。
