基于多信息融合和改进PSO-SVM的刀具磨损仿真预测

黄庆卿， 黄 豪， 张 焱， 胡小林

（1.重庆邮电大学工业物联网与网络化控制教育部重点实验室，重庆400065；2.重庆工业大数据创新中心有限公司，重庆400700）

0 引 言

近年来，随着机械领域的快速发展，应用于机械加工领域的刀具数量和种类日益增多，能否准确预测刀具磨损状态是影响企业对刀具数量采购、自身成本预算和切削参数的设定等的重要因素，对实现智能化机床有重要作用。高速铣削中的刀具磨损过程复杂、参数过多等因素导致难以准确预测刀具磨损，如何通过更加有效途径预测刀具磨损成为研究人员的关注焦点［1-4］。

国内外学者对刀具磨损预测做了大量的研究，并且取得了大量的研究成果。根据不同的监测手段，刀具磨损的检测方法主要分为直接监测法和间接监测法［5］，间接监测法相较于直接监测法，测量成本低、测量方便，能够实现实时在线监测且环境因素的噪声干扰也可以通过后期信号处理的相关技术进行去噪，故更有利刀具磨损状态的监测。在用间接监测法采集到的数据中往往包含有噪声，如果直接使用带有噪声的数据进行预测，会降低模型的预测准确度，常用的去噪方法有小波变换［6-7］、经验模态分解［8］等。间接监测法常用的有切削电流［9-10］、切削振动［11］、声发射［12］以及多传感器信号融合［13］等。在对模型选择上有不少学者采用支持向量机（Support Vector Machine，SVM）［14］、人工神经网络（Artificial Neural Network，ANN）［15］等方法对刀具磨损进行研究。相比较神经网络易陷入局部最优且过分依赖于样本的数量，支持向量机能更好地处理小样本、非线性和高维度等的分类问题，支持向量机还具有良好的泛化能力和自学习能力，但支持向量机的分类能力很大程度上取决于参数的选择，针对这一问题，很多学者采用了目前较为流行的智能优化算法对SVM进行参数优化，如皮骏等［16］提出遗传算法（Genetic Algorithm，GA）优化，Liu等［17］提出蚁群算法优化，刘成颖等［18］提出粒子群算法优化。

通过采集刀具不同磨损阶段的声发射、振动和电流等信号进行刀具的磨损状态预测。对信号进行去噪处理，将提取的时域特征和切削参数构建多维特征向量。粒子群算法与其他的智能优化算法相比，在优化参数时具有很强的鲁棒性，能够解决复杂的非线性问题，但粒子群算法也存在容易陷入局部最优和搜索准确度不高等问题，就此，提出了一种改进的粒子群优化（Particle Swarm Optimization，PSO）算法，用改进的PSO-SVM模型做分类器实现了对刀具磨损状态的预测。

1 小波去噪和改进的PSO-SVM算法

1.1 小波去噪

小波变换是一种在时、频域分析信号的方法，具有多分辨分析的特点，在时域和频域都具有表征信号局部特征的能力，在低频部分具有较低的时间分辨率和较高的频率分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，很适合于分析非平稳的信号和提取信号的局部特征，连续小波的基函数为

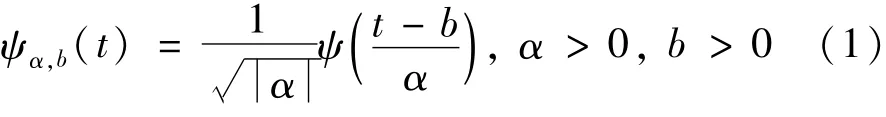
式中：α为尺度因子；b为平移因子。

在进行刀具磨损监测应用中，采集到的状态信号常为具有一定噪声的非平稳信号，可以利用小波去噪方法进行降噪处理。小波阈值去噪的基本思路是预先设定一个阈值，将信号经过小波变换得到小波分析系数，将其与初始阈值进行比较，如果小波系数小于阈值，则认为该处系数主要由噪声引起的，将其去除，达到降噪的目的。

1.2 改进粒子群算法

粒子群算法（PSO）是从生物种群行为特性中得到启发而发明的一种用于求解最优解问题的算法。其主要思想是：通过个体之间的协作和信息共享来寻找最优解：

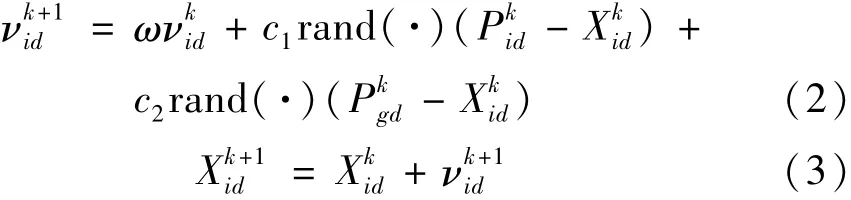
式中：ω为惯性权重；c1、c2为学习因子分别为第i个粒子的第k次迭代中的第d维的速度和位置；rand（·）为［0，1］范围内均匀分布的随机数为k次迭代中第i个粒子的个体的最优位置的第d维为k次迭代中粒子群历史最优位置的第d维。

在粒子群算法中，惯性权重体现了上一代粒子的速度对当前代粒子速度的影响程度，惯性权重越大，粒子的全局搜索能力就越强，避免陷入局部最优解，惯性权重越小，粒子的局部搜索能力就越强，使之快速收敛。针对传统粒子群算法设定固定权重的这一缺陷，提出了一种自适应惯性权重的式子为：

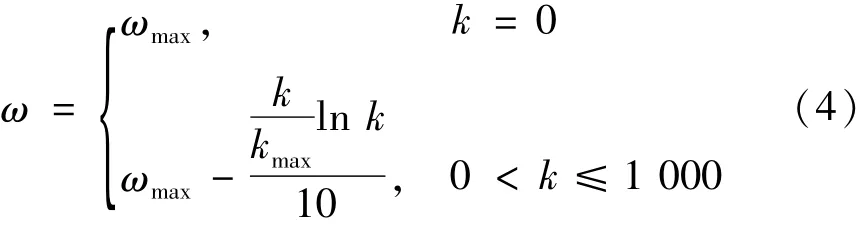
式中：ωmax为惯性权重的最大值；k为当前的迭代次数；kmax为迭代的最大次数。可见，在搜索前期惯性权重比较大，有利于算法的全局搜索，在迭代后期，惯性权重较小，粒子的局部搜索能力强，提高所求最优解的准确度。

学习因子c1、c2体现了粒子往个体最优解和全局最优解靠近的能力。提出了一种自适应调整学习因子：

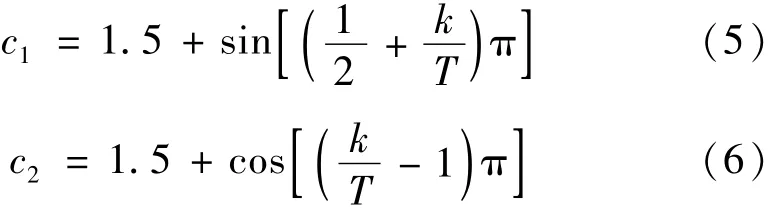
式中，T为迭代的最大次数。可见，在搜索前期，c1值较大而c2值较小，有利于全局搜索，在搜索后期，c1值较小而c2值较大，可以加快后期收敛能力。

1.3 改进的PSO-SVM算法

支持向量机（SVM）是一种基于统计学习理论的机器学方法，其核心思想是将低维空间线性不可分的数据映射到高维空间，在高维空间中构建一个最优分类超平面对数据进行区分，并将分类间隔最大化。其中SVM中的惩罚因子c和核函数参数g的选择对分类结果影响极大，故采用1.2节所述改进的粒子群算法对SVM进行参数优化，具体步骤为：

步骤1参数初始化。设置种群大小、最大迭代次数、定义适应度函数、权重ω的最大值与最小值、最大迭代次数、每个粒子的位置和速度的初始化、核函数参数g和惩罚因子c的取值范围；

步骤2计算每个粒子的适应度值，更新个体最优值和全局历史最优值；

步骤3通过1.2节中的式（2）～（6）更新粒子的速度和位置；

步骤4判断是否达到最大迭代次数，如果是则输出支持向量机的最优参数，否则返回步骤2。

用PSO优化SVM参数的具体流程如图1所示。

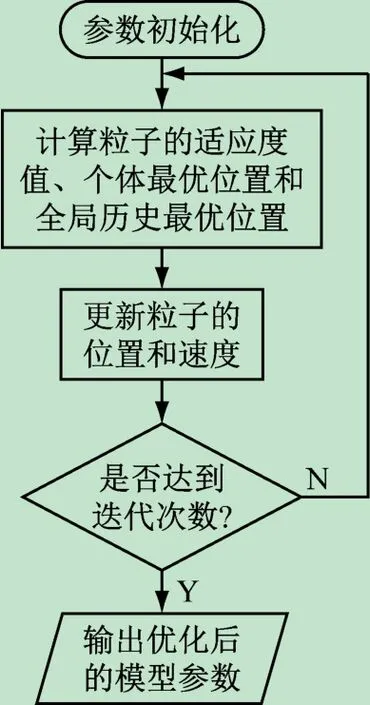
图1 改进的粒子群算法优化支持向量机参数流程图

1.4 基于改进的PSO-SVM的刀具磨损预测程序

如图2所示为基于改进的PSO-SVM的刀具磨损状态预测流程图。

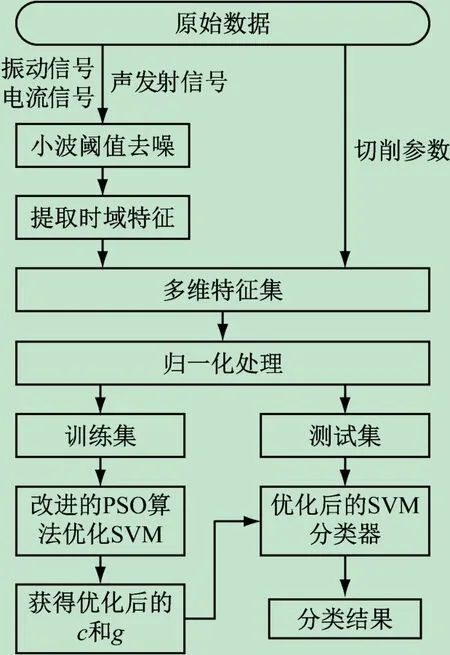
图2 基于改进的PSO-SVM的刀具磨损状态预测流程图

2 仿真研究

2.1 数据来源

铣削数据集来源于NASA数据库提供的铣刀磨损试验数据集［19］，其中包含16把铣刀在不同的操作条件下的退化数据，实验在MC-510V CNC立式加工中心的铣床上进行，通过3种不同类型的传感器分别采集工作台和主轴的振动、声发射以及主轴电动机的直流和交流信号，每加工一段时间后使用显微镜测量铣刀的磨损值并记录。

选取序号为3、11、12的刀具数据作为实验数据，3把刀具的切削参数见表1。

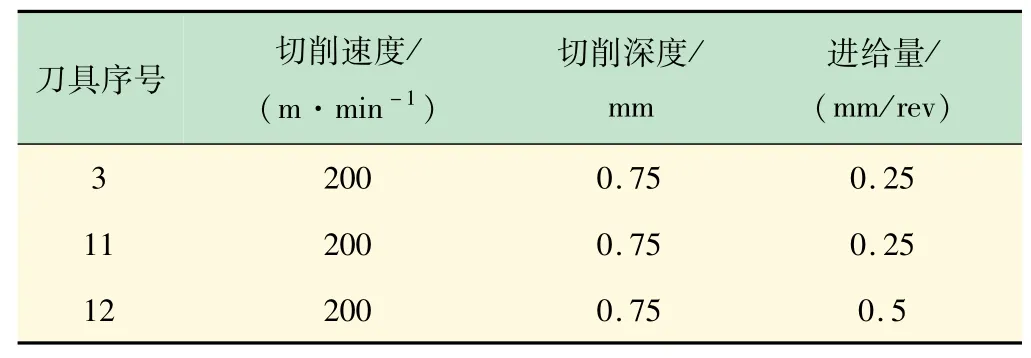
表1 切削参数

每把刀具分别取12组对应刀具磨损状态不同的数据，所取数据的磨损变化趋势见图3所示。

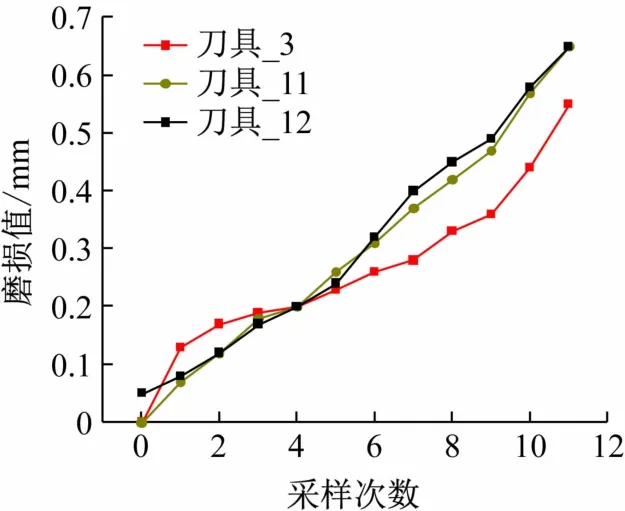
图3 磨损变化趋势图

每组数据取9 000个采样点；同时设置磨损区间，当磨损值小于0.1 mm时为初期磨损，标记为“0”，当磨损值大于等于0.1 mm且小于0.2 mm时为中期磨损，标记为“1”，当磨损值大于等于0.2 mm且小于0.3 mm时为后期磨损，标记为“2”，当磨损值大于等于0.3 mm时为刀具失效，标记为“3”。

2.2 特征提取

在对信号进行特征提取之前，需要对信号进行滤噪处理。采用“db6”小波基函数的4层分解进行信号的小波去噪，选取一个由极大、极小阈值估计方法产生的一个均方误差最小的阈值，小波阈值函数选择的是软阈值函数，即

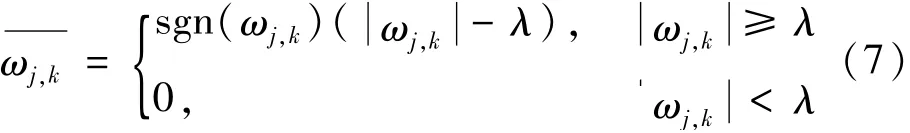
图4 是对序号3刀具的第1次交流电信号采样得到的部分数据进行滤噪前后的对比。

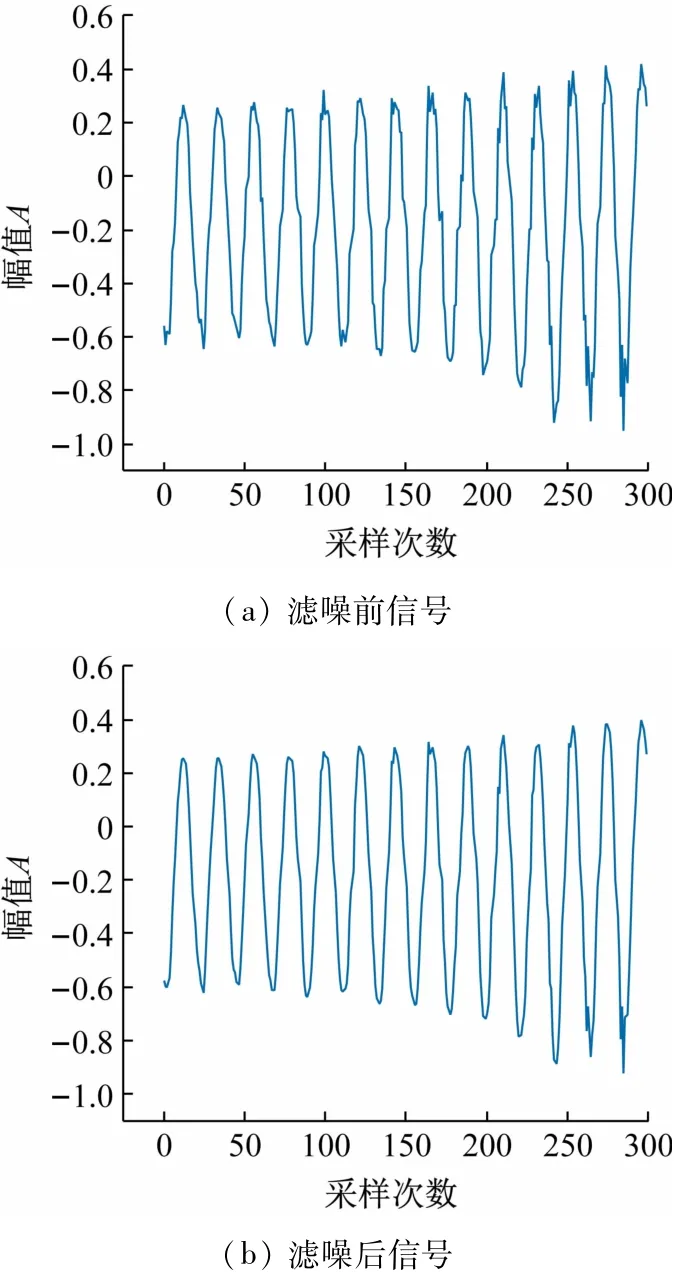
图4 滤噪前后信号对比

由图4可见，小波阈值去噪的效果比较好，较好的滤除掉了随机噪声，重构信号较好地保留了原始信号的大部分信息，滤噪后的曲线也更加光滑。

在对信号进行滤噪后，就可以对信号进行时域特征的提取，本文主要提取的时域特征有峰值因子、裕度因子、方差、脉冲因子、均值、峰值、均方根和波形因子，将得到的时域特征和切削参数（切削深度和进给量）相结合，并做归一化处理，为其作为SVM模型的优化以及模型的评估做准备。

2.3 建立SVM模型及优化

从每个类别中分别采集100组数据作为样本，共选取400个样本，其中320个样本用于训练集，80个样本用于测试集，将训练集用于支持向量机模型参数的寻优，测试集用于检测模型的准确度。利用1.3节中的方法进行SVM参数寻优，设置种群大小m＝50，最大迭代次数k＝100，ωmax＝0.9，惩罚参数C∈［0.001，100］，核函数参数g∈［0.01，100］，定义适应度函数为5倍交叉验证下的模型的准确率，寻优结果如图5所示。由图5可见，随着迭代次数增加，适应度值也在不断地增大，最终达到了1，说明本文提出的改进的PSOSVM分类器有较好的寻优能力。

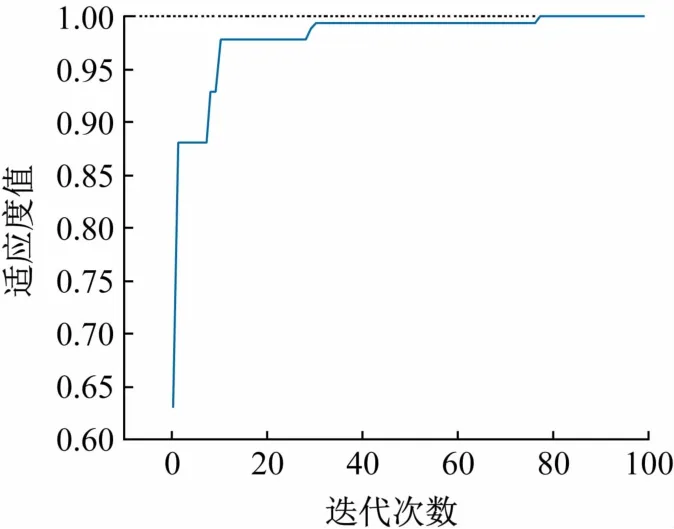
图5 参数寻优过程

为了验证本方法的优越性，分别与基本的PSOSVM模型以及GA-SVM两种模型进行对比，其中基本PSO-SVM分类器中，ω＝1，c1＝c2＝2，GA-SVM分类器中，交叉率Pc＝0.9，变异率Pm＝0.01，3种模型在训练集上的寻优结果对比如图6所示。

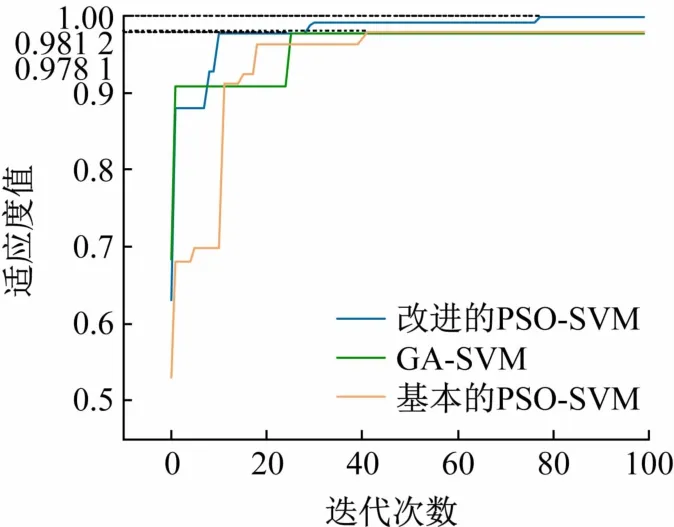
图6 3种模型的参数寻优对比

由图6可见，基本PSO-SVM和GA-SVM 2种分类器的最佳适应度值分别在0.978 1和0.981 2，其中基本PSO-SVM变化程度较小，准确度最低，GA-SVM的收敛速度上表现较差，改进的PSO-SVM在第8次迭代时准确度就已经高过其他两种模型，最终的适应度值也达到1，说明改进的PSO-SVM不仅收敛速度快，且更容易跳出局部最优点。

3种模型的最优参数分别构建优化后的3种分类器，在测试集上的准确率见表2。

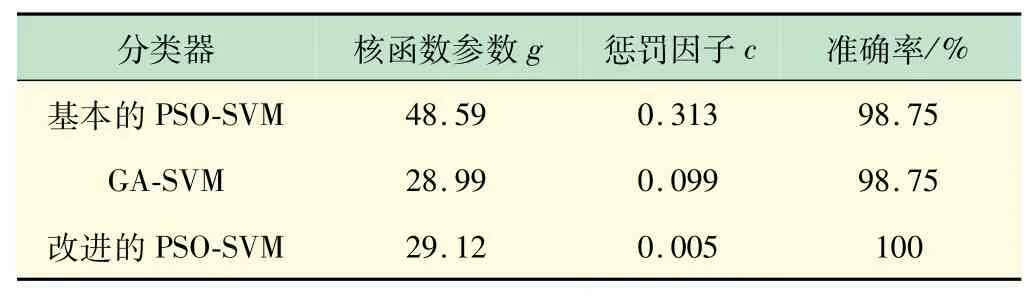
表2 3种模型在测试集上的准确率

可见，在测试集上改进的PSO-SVM模型的准确率依然是100%，其他两种模型有少量错分的现象。

3 结 语

在切削过程中，不同传感器采集到的信号可以从不同角度反映切削状态的变化，刀具切削过程中产生的振动、声音以及电流等信号等都会随着切削状态的变化而变化，利用多传感器信息融合的技术进行刀具磨损状态监测是目前一种较为理想的监测方法。

采集到的信号包含有噪声，利用小波变换方法可以对信号进行滤噪，获得更加接近于原信号的“干净”信号，有效提高信号的可用性。支持向量机被广泛用于模式识别领域，但它自身的性能很大程度上取决于参数选择，针对这一问题，提出一种改进粒子群算法优化支持向量机的核函数参数和惩罚因子。通过仿真实验对比，改进PSO-SVM模型具有较高的预测准确度，为刀具磨损状态监测提供了一种有效的方法。