S分布时滞静态神经网络的全局渐近同步性*
2021-07-27张若军
张若军, 张 垒
(中国海洋大学数学科学学院, 山东 青岛 266100)
20世纪80年代,美国加州理工学院的生物物理学家Hopfield提出的Hopfield神经网络模型[1-2]是人工神经网络研究中具有里程碑意义的工作。因为人工神经网络是人脑智能活动或部分功能的模拟,所以广泛应用于并行计算、模式识别、信号处理、联想记忆等领域,特别是在人工智能领域存在巨大潜力。尤其近三十年来,随着高性能计算机的出现及新概念的不断引入,人们对人工神经网络的研究热情高涨,并得到了大量有价值的研究成果[3-7]。
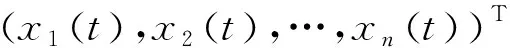
(1)
式中:τi为正常数;n表示神经网络中神经元的个数;wij表示神经元j到i的连接权重;gi(·)表示神经元i的激活函数;Ii表示神经元i的外部输入。
以神经元的外部状态y(t)=(y1(t),y2(t),…,yn(t))T作为变量的递归神经网络称为静态神经网络模型,其基本形式为
(2)
模型(2)中出现的符号意义与模型(1)相同。
相比于局域递归神经网络模型(1),静态神经网络模型(2)的研究成果较少,而静态神经网络模型包含了ReBp网、BCOp网、BSB网等重要人工神经网络模型[9]。同时,因为神经元之间的信息传输速度有限,以及电路系统中放大器的开关速度有限,不可避免地产生时滞,时滞的存在会导致网络的振动、不稳定甚至出现混沌现象,因此,时滞神经网络的研究尤为重要,而S分布时滞包含了离散时滞与连续分布时滞两种情形[10],故具有更一般的意义。
1990年代,美国数学家Pecora和Carroll[11-12]首次提出驱动—响应概念并实现了两个混沌系统的同步。此后,混沌同步控制在保密通讯、优化组合、人工智能等方向得到了广泛应用。在时滞神经网络的同步性研究方面虽然也有大量研究成果[13-19],但就作者所知,有关静态神经网络同步性的研究鲜见报道。
本文将考虑S分布时滞静态神经网络的全局渐近同步问题,以S分布时滞静态神经网络为驱动-响应系统,在一定条件限制下,设计响应系统控制器,应用Lyapunov泛函方法和某些不等式技巧,得到所考虑的驱动—响应系统的全局渐近同步性的充分性条件,该条件简单且易于应用。并且,本文最后给出了一个实例验证了所得结论的有效性。
1 主要结果
考虑如下一类S分布时滞静态神经网络模型
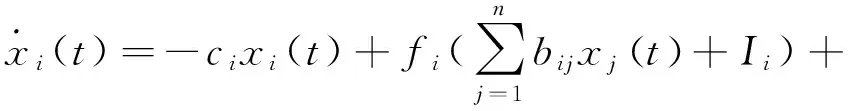
(3)

模型(3)的向量形式为
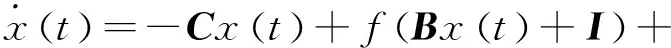
(4)
式中:
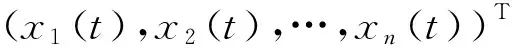
C=diag(c1,c2,…,cn),ci>0,i∈I,B=(bij)n×n;
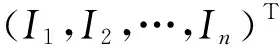
f(Bx(t)+I)=

以模型(4)为驱动系统,并设相应的响应系统为
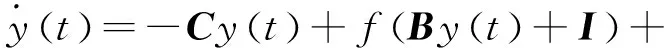
(5)
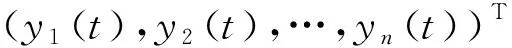
设系统(4)与系统(5)的初始条件分别为:
xi(s)=φi(s),s∈[-r,0],φi(s)∈C([-r,0],R)
(6)
和
yi(s)=Ψi(s),s∈[-r,0],Ψi(s)∈C([-r,0],R)。
(7)
为证明方便,这里给出以下假设。
(H1) 输出函数gi(·)满足全局Lipschitz条件,即存在常数lig>0,使对∀u,v∈R,有
|gi(u)-gi(v)|≤lig|u-v|,i∈I。
(H2)DLg为对称正定矩阵,且存在矩阵K,使得K+E为对称正定矩阵,这里Lg=diag(l1g,l2g,…,lng)。
定义1若对任意的初始条件,系统(4)中的状态向量x(t)和系统(5)中的状态向量y(t),满足

则称系统(4)和(5)是全局渐近同步的。

引理2若f(x)为[a,b]上的连续函数,g(x)为[a,b]上不减有界变差函数,则
证明 分两部分证明。
第一部分证明:对∀ai∈R,bi∈R,bi>0,i∈I,有
(8)
利用数学归纳法,n=1时,(8)式显然成立。
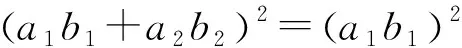
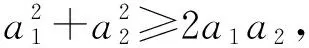
假设n=k时,(8)式成立,即有
(9)
则当n=k+1时,
第二部分证明:
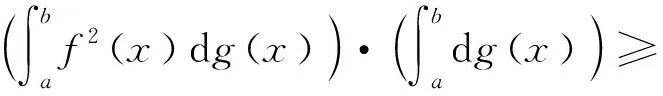
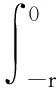
(10)
对[a,b]的某一分法Δ:a=x0 有 由第一部分证明的结论,显然有 在上式中令λ→0,故(10)式成立。 引理3[20]对∀x∈Rn,y∈Rn,有 2xTy≤xTx+yTy。 定义同步误差信号e(t)=y(t)-x(t),由驱动系统(4)和响应系统(5),可以得到如下的误差系统: -Ce(t)+f(By(t)+I)-f(Bx(t)+I)+ (11) 定理1假设驱动系统(4)和响应系统(5)满足条件(H1)和(H2),设计反馈控制器 U(t)=f(Bx(t)+I)-f(By(t)+I)+ 其中G为满足以下条件的矩阵 (12) 证明 在定理设计的反馈控制器下,误差系统(11)的零解显然存在,因此,可将证明系统(4)与(5)是全局渐近同步的转化为证明系统(11)的零解是全局渐近稳定的。 定义Lyapunov泛函 (13) 沿系统(11)的解轨道,计算V(e(t))的导数,利用引理1,有 其中 eT(t)[(G-C)e(t)+ (14) (15) 利用引理2,有 (16) 再利用条件(H1)、(H2)及引理3,有 (17) 综合(14)~(17)式,有 (18) 例1考虑如下S分布时滞二维静态神经网络系统 (19) 从而, Q= 本文讨论了一类S分布时滞静态神经网络的全局渐近同步性。在一定的条件下,设计了相应的响应系统的控制器,应用Lyapunov泛函方法及某些不等式技巧,得到驱动—响应系统全局渐近同步性的充分性条件,该条件简单且易于应用。并且,通过给出具体实例说明了所得结论的有效性。
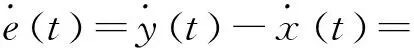


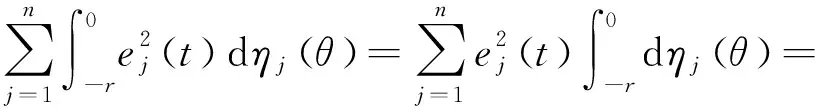
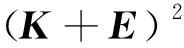

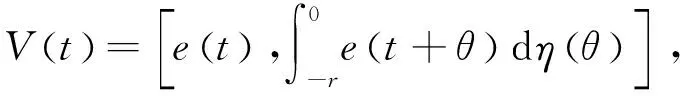
2 实例

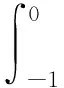
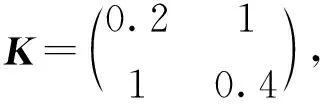
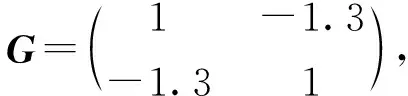
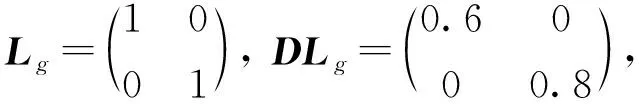
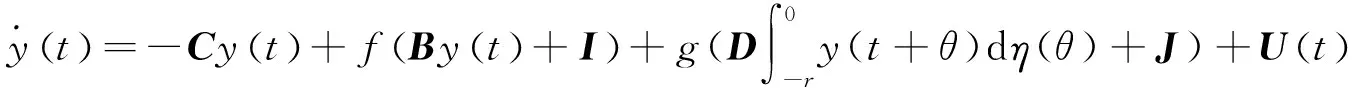
3 结语
