一种马田系统的无线传感器网络数据异常检测方法

2021-07-27张星亮

新一代信息技术 2021年5期

张星亮

（河北地质大学信息工程学院，河北石家庄 050031）

0 引言

无线传感器网络（Wireless Sensor Network，WSN）是由具备通信能力和计算能力的传感器节点组成的自组网络。由于节点低成本且部署灵活等特点，现已广泛用于农业环境监测、地质数据采集、军事侦察等众多相关领域。无线传感器网络往往部署在无人管理的或者恶劣的环境中，可能会受到其他信号的干扰、自身电量限制和环境异常变化而导致数据出现异常，进而使得无法进行后面的数据计算和分析。因此在部署无线传感器网络时需要将对数据的异常检测考虑在内。

近些年来，一些专家和学者对无线传感器网络中的异常数据检测做了很多突出贡献。Bilal[1]等人提出了一种基于 K-medoid定制聚类技术的混合异常检测方法，该方法适用于无线环境下包括误向和黑洞攻击的混合异常检测。Mahmood[2]等人一种基于局部时间序列的无线传感器网络数据噪声与异常检测方法，采用自适应贝叶斯网络作为分类算法，能够对每个传感器节点的异常值进行局部预测和识别。Murad[3]等人提出了一种基于单类主成分分类器（OCPCC）的WSN分布式异常检测模型，该模型利用了封闭邻域中感测数据之间的空间相关性来对异常进行检测。郑文添[4]针对WSN的异常数据检测，以PCA算法为基础结合马氏距离提出改进型分布式主成分异常数据检测方案，能够提高了网络中异常数据的检测性能并同时降低网络中的通信资源开销。邓丽[5]等人提出一种融合数据流时空特征和多分类模型的异常检测算法，算法首先基于 Markov链提取传感器数据流的时空特征，然后将时空特征作为多分类卷积神经网络模型的输入特征，对数据流进行异常检测及异常类型识别。

马田系统是一种用于多变量数据的判别预测方法，并且马氏系统的应用十分广泛。Ning Wang[6]等人提出了一种基于改进 MTS的设备状态特征识别与选择模型，研究了模型的两个方面，即原始马氏空间的构造和阈值的确定。Wenhe Chen[7]等人利用马田系统通过六个维度：收入、教育、健康、生活、资产和住房，能够准确识别贫困户和非贫困户。

彭宅铭[8]将马田系统应用在对滚动轴承的状态监测中，根据时域、频域和自适应白噪声来分析轴承故障发展趋势。彭宅铭[9]利用航空发动机的健康状态进行评估，为航空发动机的状态分析提供了一种新方法。王海燕[10]和吴敬之[11]分别将马田系统应用到航空客运服务的评价和工业运行质量的评价，拓展了马田系统的应用。

本文将利用马田系统来对无线传感器网络中所采集数据进行异常检测。

1 马田系统

马田系统是由日本统计学家田口玄一博士提出的一种用于多变量数据的判别预测方法。马田系统是由马氏距离和田口方法组成。马氏距离不仅仅是一种距离的度量，而且还可以用来表示数据之间的协方差距离。它是把属性之间的相互联系考虑在内，并且是与数据的测量单位无关。马氏距离是用来区分异常数据和正常数据，将区分之后的正常样本的马氏空间上通过田口方法的正交表和信噪比来对主要的特征变量进行筛选，达到优化特征测量表，进而为后面的计算降低复杂度。将优化之后的马氏空间对异常数据和正常数据进行阈值划分，当再遇到未知的样本数据时，可以直接利用已经计算好的阈值，直接进行分类和预测。利用马田系统将异常数据划分出来之后，对于异常数据将不再信任，本文将利用第四章方法对不信任的异常值进行补值。

本文将具体的实施步骤可以分为4步：构建马氏空间、马氏空间的验证、马氏空间的优化、分类和诊断。

1.1 构建马氏空间

马氏空间就是由马氏距离构建的矩阵，马氏空间对马氏系统的有效性和可靠性有着极其重要的影响，这也是构建马田系统最首要的步骤。首先需要选出进行构建空间的正常样本并确定特征量，先将选定的特征变量进行计算平均值和标准差，并以此来对数据进行标准化。将标准化的正常样本的马氏距离构成马氏空间。

马氏距离是由印度统计学家马哈拉诺比斯提出的，是用来表示协方差的距离，一种来表示未知特征集合相似度的度量方式。马氏距离相对于欧氏距离来说，马氏距离不仅对变量之间的相关性极其敏感，而且还能消除变量之间的相互干扰；而欧氏距离只是单纯的计算变量之间的距离值，无法对变量之间的相关性和变量之间是否存在相互干扰做出判断。

马氏距离通过被测样品与马氏总体之间的距离，来体现样本之间的相似程度。本文中使用施密特正交法对马氏距离进行计算，所以这里只对施密特正交法进行介绍。对于逆矩阵法的马氏距离求解的具体步骤如下：

（1）假设多元系统中有p个变量，并设为vj，其中j= 1 ,2,3,… ,p，通过p个变量来进行界定正常数据的样本空间。

（2）在系统的p个变量下，进行收集容量为n的样本数据，数据vij是第j个变量中第i次的测量值，其中i= 1 ,2,3,… ,n。

（3）将测量的样本数据进行标准化，

其中Zi表示正常样品中第i个标准化的数据，其中i= 1 ,2,3,… ,n。

通过相关系数矩阵可以得到马氏距离，但是相关矩阵可能存在多重共线问题，进而影响模型的稳健性。为了避免多重共线问题，可以利用施密特正交法来进行马氏距离的计算。先是通过对p个变量进行标准化为：

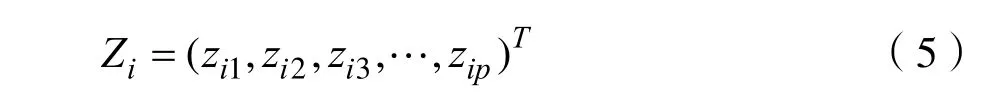
其中i= 1 ,2,3,… ,n。将标准化的向量组进行施密特正交化。

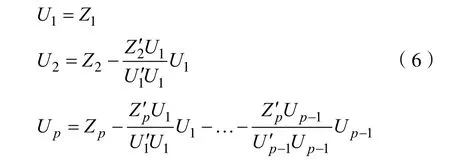
进而得到的马氏距离为：

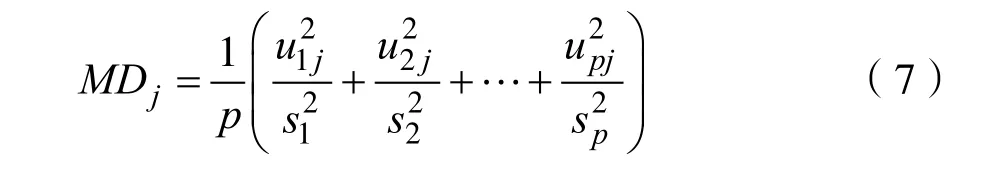
1.2 马氏空间的验证

由于马氏空间是通过正常样本进行构建的，所以马氏空间的有效性还需要检验，若该马氏空间能够将异常数据和正常数据进行区分，那证明该马氏空间是有效的，否则需要重新构建马氏空间。在进行马氏空间验证时，需要计算异常数据的马氏距离的均值，并以此与正常数据的马氏距离均值进行比较，如果大于正常数据的马氏距离均值，那说明由第一步构建的马氏空间是有效的。其中在计算异常数据的马氏距离时，用到的样本均值和标准差均是采用正常样本的。

本文中的异常数据的马氏空间也是利用正常数据的均值和标准差将数据标准化，利用施密特正交化构建的异常数据的马氏空间。如果正常数据的马氏空间远远小于异常数据的马氏空间，则说明由正常数据构建的马氏空间有效，否则需要重新选择样本数据来重新构建马氏空间。

1.3 马氏空间的优化

在选定的所有原始变量中，并不是所有的变量都对异常检测有贡献，所以在构建马氏空间之后要对马氏空间进行优化，这样不仅能对数据降维，也能为后面的计算降低复杂度。本文使用正交表和信噪比来对马氏空间进行优化。

1.3.1 正交表

正交表是带有规则的设计表格，而在马田系统中则是根据初始变量的不同来选择相对应的正交表。在正交表中，每一行对应着每一组实验，“1”是选择该变量，“2”是不选择该变量，这样将会对变量进行选择，将被选择的变量来组成马氏空间。

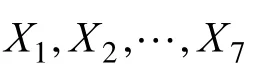
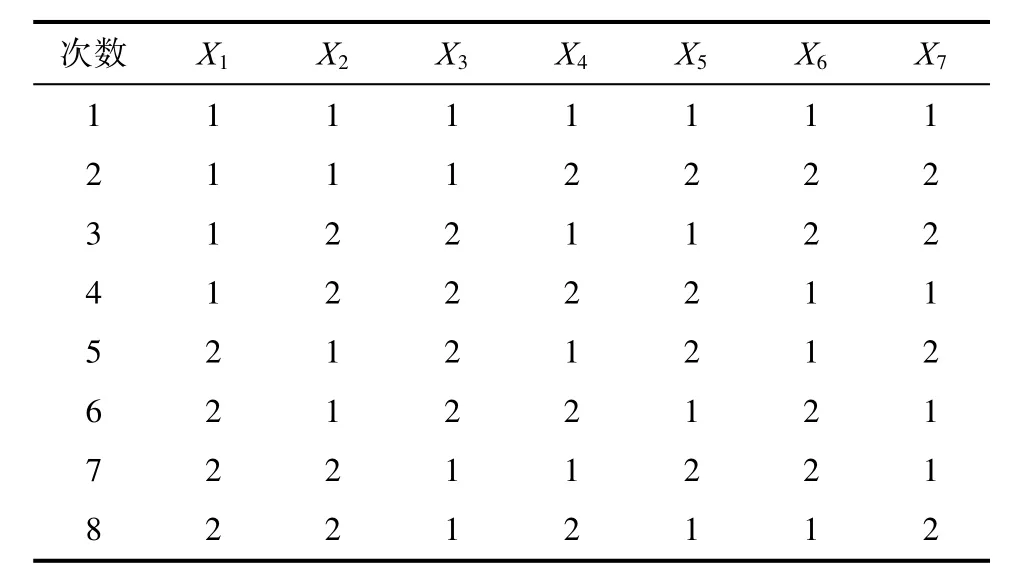
表1 L8(27)的正交表Tab.1 The orthogonal table of L8(27)

在表中第一次试验对应的变量选择为1、1、1、1、1、1、1，即每个特征变量的水平为“1”，由此可得组成马氏空间的特征变量为X1、X2、X3、X4、X5、X6、X7。而表中的第二次试验的变量选择为 1、1、1、2、2、2、2，前三个的特征变量都为“1”，后四个的特征变量都为“2”，由此组成的马氏空间的变量为X1、X2、X3。将使用选择的特征变量来计算正常样品和异常样品的马氏距离。

1.3.2 信噪比

信噪比（Signal Noise Ratio，SNR）通常是用在通信行业中，用于对电子设备或电子系统的通信的评价。在通信行业中，信噪比是接收到的信号功率和噪声功率的比值；而在马田系统中是通过信噪比来使马氏距离的偏离程度放大，进而能够选择对异常检测贡献较大的特征变量。本文采用正交表和信噪比来筛选特征变量。

信噪比不仅能评价筛选之后的特征变量的可靠性和稳健性，还能对筛选的特征变量组的功效性进行评价。当对异常数据进行评价时，在不了解异常数据的情况下，相对于正常数据，希望异常数据的偏离程度越大越有利于数据的辨识，本文采用望大特性信噪比来进行计算。假设异常样本的数目为n，采用施密特正交法计算得到的马氏距离为MD1,MD2,… ,MDn，则正交表进行的第i次实验的望大特性信噪比为：

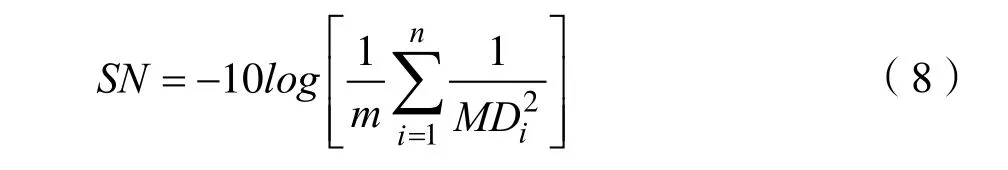
在引入信噪比之后，需要对特征变量进行部分剔除和保留，因此引入信息增益差ΔSN：

1.4 分类和诊断

将筛选过后的特征变量重新计算正常数据和异常数据的马氏距离和马氏空间，并与原始马氏空间进行对比，验证优化后的马氏空间的是否改善。利用优化后的马氏空间和阈值λ来对未知的样本进行分类和识别。对于未知样本的分类和识别，本文采用f极大值方法来确定阈值。

在马田系统的应用及实践中，阈值的确定对异常数据的判断有着极其重要的意义，阈值的好坏直接影响着系统的好坏以及对数据的判断结果。马田系统的阈值确定一直都备受关注，田口玄一博士利用二次损失函数（Quality Loss Function，QLF）对阈值进行计算，二次损失函数是凭借专业人员的判断和损失数据来对阈值进行判断，这样得到的阈值会有很大的主观性。本文采用f极大值法来确定阈值。

设T为阈值，通过施密特正交法计算的正常样本的马氏距离MDi，i= 1 ,2,…,n，而异常样本的马氏距离为MDi，i=n+ 1 ,n+ 2,…,n+m。

其中i= 1 ,2,… ,n。

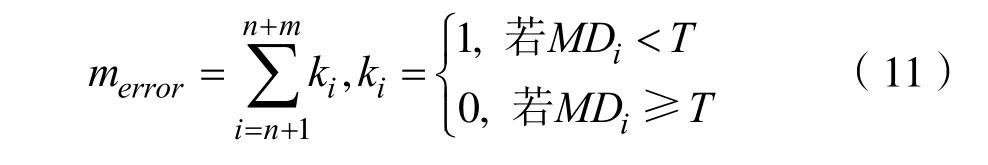
其中i=n+ 1 ,n+ 2,… ,n+m。

则正常样本进行分类的正确率为：

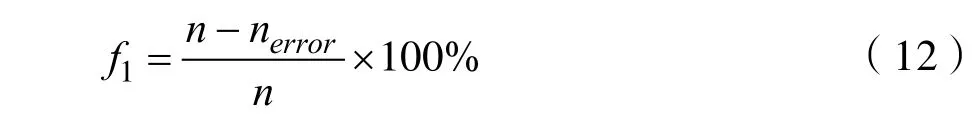
异常样本进行分类的正确率为：

设极大值f=f1×f2，f值最大时求得T值为马田系统的阈值。具体算法表示

在阈值确定之后，对于未知的样本数据，可以利用本文提到逆矩阵法、施密特正交法、伴随矩阵法构建相对应的马氏空间，并通过计算好的阈值与马氏距离相比较，进而能够对异常数据进行判定和识别。

2 实验分析

2.1 数据来源

本文使用python进行实验，并对真实数据集上进行本文实验，测试所用的数据集是由部署在英特尔-伯克利实验室的54个传感器节点在36天内产生的采集数据。这些采集数据分别是对温度、湿度、光照强度和节点电压每隔30 s进行一次采样所得的采集值。本文选取节点19在2004年3月8日所采集的数据，每隔15分钟进行一次数据选取。

2.2 实验分析

本文将以时间序列为依据，采用随时间的变化的传感器的数据为马氏系统的特征向量，特征向量将由温度、湿度、光照强度、电压组成。表2将要进行异常数据监测的特征变量。

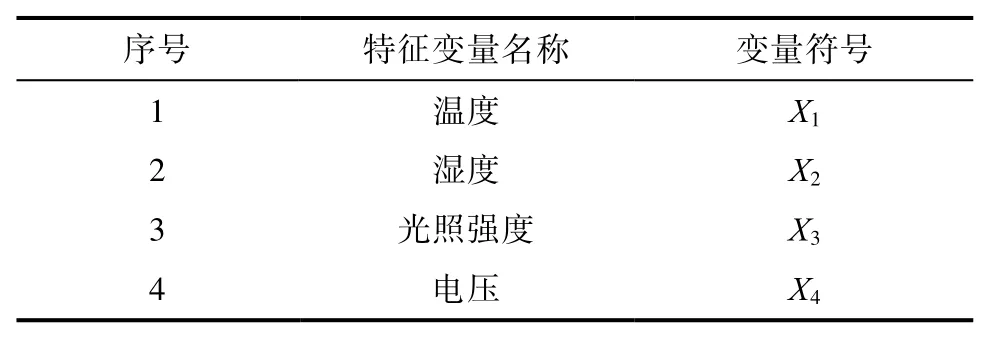
表2 农业数据的特征变量Tab.2 Characteristic variables of agricultural data

利用施密特正交法对特征变量计算正常样本的马氏距离，如表3所示。

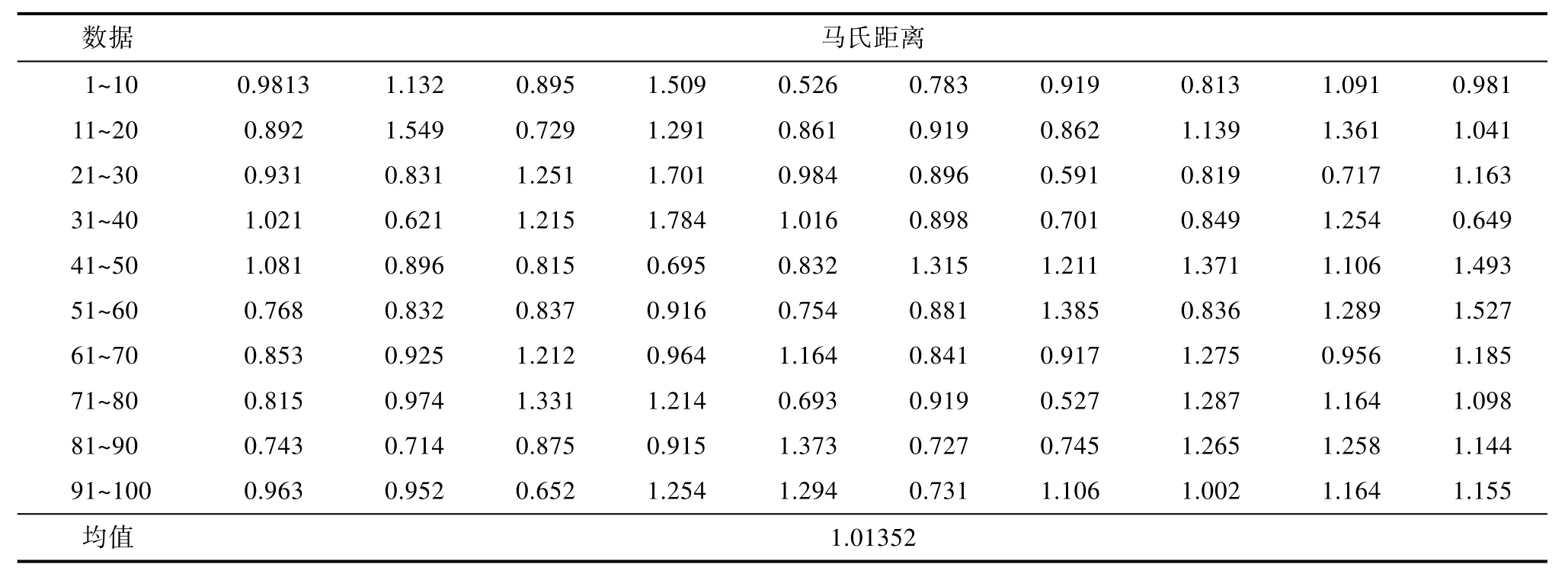
表3 正常样本的马氏距离表Tab.3 Mahalanobis distance table of normal samples

通过表 3正常数据的马氏距离可以看出，马氏距离的均值 1.01352≈1，但可以看出选取的正常样本数据是有效的，但是单从正常数据的马氏距离是不能看出该特征变量的数据是否有效，还要与异常数据的马氏距离进行比较，通过观察异常样本的马氏距离的偏离程度来确定选取的数据是否有效。

异常数据是正常数据之外的数据，在本文中将模拟异常数据，使用python随机产生30个异常数据进行试验。本文将模拟采集数据错误、终端节点掉电、节点被攻击、发送数据超时等多种情况的发生，尽可能的使异常数据还原到真正的异常情况发生。异常数据的马氏距离如表4所示。

表4 异常样本的马氏距离表Tab.4 Mahalanobis distance table of abnormal samples

由表 2中数据可以得知，异常数据的马氏距离的均值为 8.0142，并且与正常样本的马氏距离存在明显的差异，异常样本的马氏距离是远远大于正常样本的马氏距离，由此创建的马氏空间是有效的。若是异常样本的马氏距离与正常样本的马氏距离存在的数据差异较小的话，则需要重新选择数据来重新构建空间。

2.3 马田系统的优化

在系统中并不是数据的特征量越多就代表数据越详细，就能较全面的展现系统中的变化。有些特征量能直观的反应农业数据的变化，有利于提高识别数据中存在的异常值，但是有些数据是不能直观的展现数据变化的，因此需要将这些不能直观展现数据变化的冗余数据给去除掉。在本文中则使用正交表和信噪比进行冗余数据的筛选，筛选出对判别异常数据有用的特征变量，从而能够达到降维的目的。

其中“1”表示选择该特征变量进行计算信噪比，“2”则相反，即不选择该变量进行计算信噪比。每一行都对应所选取的特征变量来构建马氏空间，即每行对应着一个马氏空间，由表中可知总共为8组实验方案。在选定每行的特征变量之后，再进行计算选定之后异常条件下的马氏距离，最后再计算马氏距离所相应的信噪比。

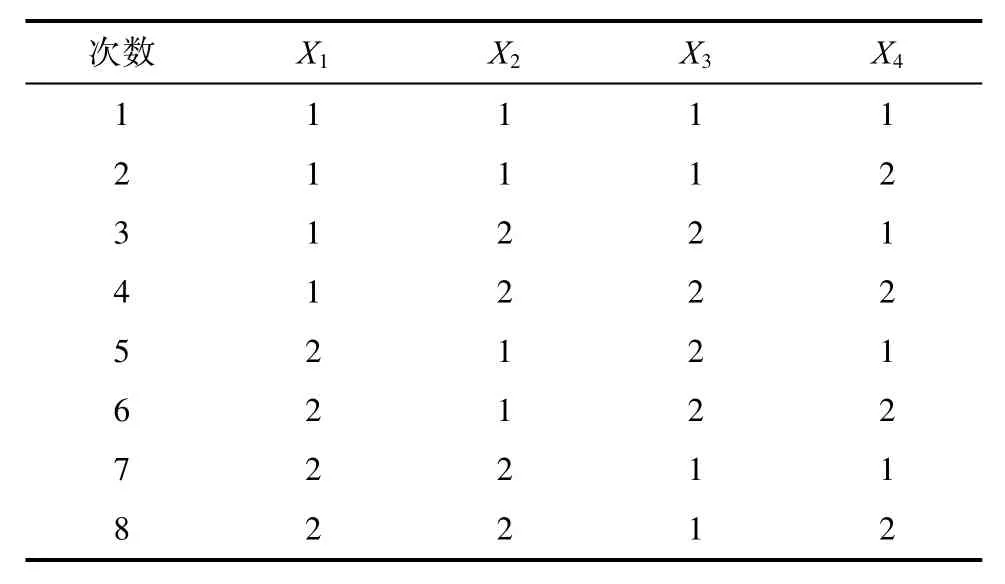
表5 L8 (24)的正交表及变量选择Tab.5 The orthogonal table of L 8 (24)and variable selection

在选定各组特征变量后，通过对各组的被选中的异常情况下数据进行标准化和施密特正交化，进而得到马氏距离而构成的子马氏空间。30组异常条件下的特征变量在表4重新构建的马氏空间下所对应的马氏距离的均值，如表6所示。

表6 8 次实验所对应的马氏距离的均值及信噪比Tab.6 Mean value and SNR of Mahalanobis distance corresponding to eight experiments

在计算正交表所重构的马氏距离和马氏距离所对应的信噪比之后，还需要与重构马氏空间后剩下的部分特征变量所形成的信噪比进行对比，进而形成信息增益，如表7所示。

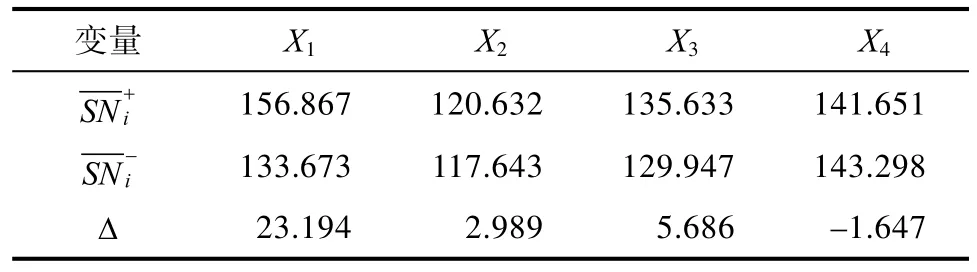
表7 信息增益表Tab.7 Infor mation gain table

2.4 分析与诊断

在多元系统变量中，决策阈值对判别的有效性有着重要的作用。传统的马田系统使用质量损失函数方法确定决策阈值，但是真实情况下质量损失是专业人员根据平常的经验和积累规定的，所以质量损失函数在确定阈值的过程中会存在主观性，由此方法得到的阈值准确度不高。采用f极大值方法来确定阈值，为了使是实验结果准确本文采用穷举法来确定阈值，虽然消耗的时间长点，但是整体具有较高的准确性。具体的算法描述如算法1所示。

算法1f极大值计算阈值伪代码表示

Algorithm.1 Pseudo code representation of f-max calculation threshold

f极大值计算阈值伪代码表示

输入：正常样本的马氏距离、异常样本的马氏距离。

输出：判断正常样本马氏距离的阈值T。

MD_Nor_Data、MD_Abnor_Data分别是正常数据和异常数据所对应的马氏距离。

Step.1whilej＜ max(MD_Nor_Data)/*使用最大马氏距离来当作循环的终止点*/

Step.2forindextolen(MD_Nor_Data)

Step.3 统计正常数据的马氏距离中大于j的个数

Step.4forindextolen(MD_Abnor_Data)

Step.5 统计异常数据的马氏距离中小于等于j的个数

Step.6 记录正常数据马氏距离的正确率f1