一种高效的不确定图上k步可达查询处理算法
2021-07-27周军锋
仲 悦,杜 明,周军锋
(东华大学,上海 201620)
0 引言
k步可达查询用于研究在给定的数据图上,起始点u是否能在路径长度不大于k的前提下到达目标顶点v。该研究有着广泛的用途[1-3],例如在人际关系网络图[4]中,查询两个人能否通过 k个中间好友构成熟人关系;道路网络[5]中,用以查询用户是否可以从一个起点经过k条道路到达目的地等。
目前已有的 k步可达查询研究都是基于确定图[6-10],然而不确定图[11]在实际生活中随处可见,此时两个实体之间的联系的强弱程度表现为边上的概率权值。例如,在道路网络中时常会出现拥堵的情况,而拥堵的严重程度可以用概率来刻画,从而导致本来可达的路径暂时性不可达;以及路由网络中,传感器测量误差导致两个路由之间的信号不稳定也会产生不确定的边。当给定一个不确定图,k步可达查询不但要求两点间可达,而且还要求出可达的概率。最朴素的方法是枚举所有的可能世界及其出现概率,接着计算每一个可能世界上u到v的可达情况,将结果相加。而每一个可能世界由于边的出现情况不同,无法用预先处理的索引对不同的可能世界进行查询。一个n条边的不确定图有2n个可能世界,呈指数级。因此,即使该方法能得到最精确的结果,当数据图达到比较大的规模后,这种枚举法显然无法进行,不具有扩展性。
针对上述问题,本文提出一种两阶段查询方法,用于加速不确定图上k步可达查询的处理。其基本思想是:对可达和不可达的查询基于不同索引分别处理。对不可达查询,提出基于顶点覆盖的高效索引来快速检测是否k步不可达。对可达查询,构建位向量索引提前存储可能世界来加速判断。其总体思想是根据大数定律用抽样近似法进行计算,再用较小的内存提前存储抽样结果。实验结果验证了本文提出的索引和查询方法 kRP的高效性。
1 问题定义及相关工作
1.1 问题定义
给定一个有向无环不确定图G=(V,E,P),其中V是图中所有顶点的集合,E是图中边的集合,(u,v)表示从顶点u出发到顶点v有一条边,在有向图中(u,v)和(v,u)是两条不同的边,P是所有边上概率的集合,且P={pi|0<pi≤1,pi为第i条边上的概率权值}。
以下介绍不确定图、可能世界等相关定义及问题的定义。
定义 1 不确定图在图中,边上有权值,权值范围在(0,1)区间内,且权值表达的含义为该边出现的概率,将这样的图表示为G=(V,E,P),如图1。

图1 不确定图GFig. 1 Uncertain graph G
定义2 可能世界对于不确定图G=(V,E,P),若一个确定图 G′=(V′,E′)满足:(1)V′⊆V;(2)E′⊆E,则G′为G的一个可能世界。当V′=V且E′=E的时候,G′称为 G的完全图。图2是图1的两个可能世界。

图2 不确定图G的两个可能世界Fig.2 Possible Worlds of Uncertain Graph G
定义3 k步可达在一个确定图上,给定顶点u和顶点v,存在一条从u到v的路径且路径上的边数不大于k,则称u到v在k步以内可达,结果为TRUE或FALSE。

问题定义 给定一个不确定图G、顶点u和顶点v,以及步数约束k,求u到v在k步以内可达的概率值。
1.2 相关算法
1.2.1 确定图上k步索引
确定图上的 k步可达研究目前已经有不少算法,文献[7]提出了一种在顶点覆盖集上建立路径信息的索引。基本思想是随机选取一条边,将边两端的顶点都加入到覆盖集C中,删除这两个顶点的所有出边和入边,再重新随机选取一条边,重复以上操作直到图中没有剩余的边,然后在覆盖集上建立k步以内的路径传递闭包。
由于索引是在覆盖集的基础上构建的,因此查询可以分为三种情况,分别是(1)u和v都是覆盖集C中的顶点,此时只要查询索引中u到v是否 k步可达就能直接得出结果;(2)起始点 u是覆盖集C中的顶点而目标顶点v不在覆盖集内,这种情况下把问题转换为是否存在一个顶点w,且w是v的入结点,满足u到w的距离不大于k-1(u不在覆盖集中且 v在覆盖集中的情况类似,不再赘述);(3)u、v都不在覆盖集里,此时查询能否存在w1和w2,且w1是u的出结点,w2是v的入结点,满足w1到w2的距离不大于k-2。
这种索引方法存在规模大、效率低两个问题,覆盖集的大小直接影响了索引的大小和性能,然而对于覆盖集的选取过于随机性,导致生成的索引每次都不同。并且,该方法没有考虑边的不确定性,只能运用在确定图上。
1.2.2 MC抽样法
在不确定图中进行蒙特卡洛(Monte Carlo)抽样[12-13]是求解可达性问题的一种基本方法,主要思想如下:从起始点u出发BFS遍历进行不同可能世界的抽样,只有当边(u,w)存在时,才把顶点w加入BFS的运算队列中。在队列为空前,如果找到了目标顶点v,则该可能世界中两者可达,继续下一次的图抽样和可达判断。最终的结果为

1.2.3 其他方法
YILDIRIM在文献[1]中提出GRAIL算法进行可达性查询,首先用不同遍历方式生成d个区间标签加速不可达判断,对于使用标签会产生误判的查询对,提出使用特例列表进行记录,减少查询时的遍历操作。
文献[2]提出的 BFSI-B将查询分为可达和不可达进行处理,先构建深度优先生成树,再基于树利用区间标签判断可达性,如果满足区间包含要求,则计算两顶点在树中的层数差是否不大于k,从而得出k步可达查询结果。
Yano等人在文献[9]中提出 PLL算法,该方法为每个顶点 u建立inLabel和outLabel两组标签,分别用来记录能到达u的顶点和距离以及从u出发可达的顶点和距离。当查询时只需要求起始点的 outLabel与目标顶点的 inLabel中的交集顶点,通过判断两段距离相加之和与k的大小关系进行判断。
2 两阶段求解算法
对于给定两点u和v的k步可达查询,基本方法是从u出发,进行N次抽样,统计这些可能世界中既满足可达又满足k步的样本个数,除以N值得到结果。这种方法存在大量冗余计算。例如,在图3给定的有向无环不确定图中求顶点v0到顶点v1的3步可达概率,按照以上方法,需要从顶点 v0出发对边依次进行抽样。然而从顶点v0出发,无论怎么抽样都不可能到达顶点v1。事实上,在这种无法k步可达的情况下直接抽样毫无意义。对于该问题,本文提出结点覆盖索引快速判断不可达情况,从而能够避免抽样的昂贵代价。另外,对于可能到达的情况,本文提出高效的索引来加速查询处理。下面分别进行介绍。
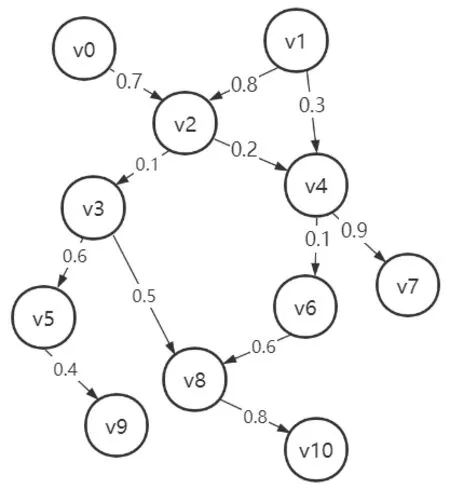
图3 有向无环不确定图Fig.3 Directed Acyclic Uncertain Graph G
2.1 顶点覆盖索引
本文首先在不确定图对应的完全图上构建顶点覆盖集,接着基于覆盖集中的顶点构建k步索引,用来判断给定查询是否能在确定图上k步可达。只有在确定图上k步可达的前提下,才需要计算它的可达概率,否则无需进行抽样操作。和k-reach算法构造覆盖集的方法不同:k-reach是通过随机选边的方式来构造覆盖集,然后计算覆盖集中两两顶点之间的最短路径。
本文在构建索引时选用的边并非随机抽取,而是优先选择度较大的顶点加入到覆盖集。因为随机取边的操作不仅会导致每次生成的顶点覆盖集和索引都不一样,索引效果也无法保证。
例如,用 k-reach算法对图 3中不确定图 G的完全图进行顶点覆盖计算的可能情况如下。假设第一次随机取边结果为 v1->v2,将顶点 v1和顶点v2加入结点覆盖集C,删除顶点v1和顶点v2的所有邻边,即边 v1->v4、v0->v2、v2->v3和v2->v4。第二次随机取边 v4->v7,相应的将顶点v4和顶点v7加入覆盖集C,并删除邻边v4->v6。若第三次和第四次随机取到的边分别为 v6->v8和v5->v9,那么此次求解覆盖集的过程如表1所示。可以看到最终求得的覆盖集C仍有8个顶点,对图的压缩效果较差。

表1 求解覆盖集过程Tab.1 The progress of computing vertex cover
但是如果按照大度顶点进行求解的话,能获得更小的顶点覆盖集,生成的索引在查询时也更高效,具体操作如下。首先选取度最大的顶点,即顶点 v2,删除 v2的邻边。然后选取当前度最大的顶点 v4,删除 v4的邻边。第三步选择剩余图中度最大的v8,最后选择顶点v5。可见,用这四个顶点就能构成原图的顶点覆盖集,比随机选边的方式减少了一半的顶点规模。


图4 完全图的kR+索引Fig.4 The kR+ index
关于索引构建的具体代码设计如下。
算法1kR+(完全图G=(V,E))
输入:完全图G=(V,E)
输出:基于顶点覆盖集VC的索引kR+
算法1用来构建完全图上的索引,加速判断k步不可达的情况。第 1~7行按照上述大度顶点的方法构建顶点覆盖集,第1行初始化顶点覆盖集VC为空集,第2行判断是否有剩余边,|E|表示边数,第 3行选择当前度最大的顶点赋给 u,在第4行加入覆盖集VC,第5~6行删除u的所有邻边并将邻接点的度都减去一。第8~11行基于顶点覆盖集构造k步索引,对于顶点u和顶点v,若u能在k步以内到达v,则给边(u,v)赋予权值,表示路径步数,否则不建立边。最后生成kR+索引。
查询时,如查询顶点v1到顶点v5是否3步可达,由于v1不在覆盖集内而v5在覆盖集内,则问题转换为查询顶点v1的出结点到顶点v5是否2步可达。顶点v1的出结点为v2和v4,由kR+索引查询可知v2到v5在2步内可达,因此得出结论v1到v5可以3步到达。
2.2 基于路径的提前抽样
本文采用文献[14]中提出的离线抽样思想,把N个可能世界提前进行抽样并且以位向量[15]的索引形式存放在边上。边存在时记为 1,不存在记为0,第i个值表示在第i个可能世界上该边的存在与否,每一条边都有一个N大小的位向量,如[01100]可以看作5个抽样图中某一条边的出现情况,该边在第二、第三个可能世界上存在。由于该索引只需要0和1两种值,因此可以采用C++中STL容器bitset或者二进制int的存储方式,从而节省索引所占内存,时间复杂度为O(K|E| ),其中N是抽样个数,|E|是边数。
求解不确定图上两点间 k步可达概率的一个重要前提是它们之间能够可达,而这一点可以用完全图上的顶点覆盖索引进行判断。倘若在完全图上无法满足k步可达,那么在任何一个可能世界中都不存在符合要求的路径,此时查询结果为0.如果完全图的查询结果为TRUE,再通过路径枚举剪枝可能世界中的边,缩小查询范围。
例如,在图3上求v2->v8在3步内可达概率,有 v2->v3->v8 和 v2->v4->v6->v8 两条路径。此时看 v2->v3和 v3->v8这两条边的第 1位,只有两者都为 1的时候这条路径才完整存在并且满足 3步可达,此时不再需要验证 v2->v4->v6->v8 路径,只有在前一条路径不符合要求时才进行第二条路径的查询。
本文提出枚举路径的时候可以采用 kDFS的方式,求解的如果是k步可达问题,则用一个大小为k+1的栈,把起始点压入栈中,如果存在未被访问过的邻居顶点就依次入栈。与DFS不同的是该栈有固定大小,如果栈满时还未到达目标顶点,则需先弹出栈顶元素后再入栈其余顶点,直到栈空。kDFS的过程中若遇到了目标顶点,就把栈中所有元素记录下来,作为一条可能路径,该方法的时间复杂度为O(|Gk(u) |),即从源顶点 u 出发k步内可以到达的顶点个数。
2.3 查询算法
算法2给出了在不确定图G上查询两点间k步可达概率的kRP方法,设计代码如下。
算法2 kRP(u,v,k,N)
输入:起始点u,目标顶点v,步数k,抽样个数N
输出:u到v在k步内可达的概率

第一行中success用来计数可能世界里k步可达的数量。第2行是在生成的顶点覆盖索引上进行查询,若u不在覆盖集内,则转换为u的出结点与v的k-1步查询,v不在覆盖集内的情况不再赘述。如果该步骤判断结果为 TRUE,则用固定大小的栈执行深度优先遍历kDFS枚举u到v的k步路径。第5~9行,在预先存储的N个可能世界中进行查询,当路径存在且查询结果为TRUE时,给计数器 success的值增加1。第10行用可达的抽样图个数除以总的个数N,即可得到概率结果。
3 实验分析
3.1 实验环境
本文实验所使用的硬件平台是Intel Core i7,主频为2.60 GHz的CPU,RAM内存为8 GB,操作系统为 Windows10 64位系统。代码用 C++实现,使用基础BFS抽样法进行比较。查询的距离k取值为3,抽样个数N为1000个,查询对数100对,其中3步内可达的顶点对数和不可达的顶点对数各占一半。
3.2 数据集
本文使用8个数据集对实验进行验证,Amaze和 Kegg都是与生物基因相关的网络图;Human和 Pubmed描述的是蛋白质网络;Nasa是 XML文档的数据集;Yago用来描述语义库中的关系结构;Arxiv来自文献[16];Web-Google是 Google网页相关的数据集,具体信息见表 2,|V|表示顶点数,|E|表示边数。边上的概率权值用随机数生成,取值为(0,1)的左开右闭区间。查询集用完全图随机生成 100对查询对,3步可达与不可达的比例为1∶1。
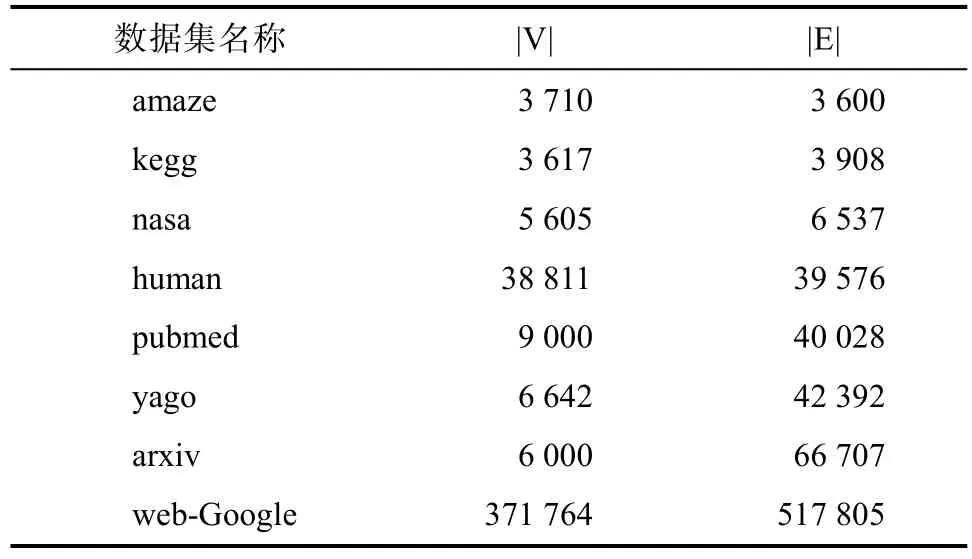
表2 数据集Tab.2 Dataset
3.3 性能比较分析
3.3.1 索引大小
表 3展示了在不同数据集上构造的索引大小,单位均为MB。其中,kR+是本文提出的用顶点覆盖集构造的k步路径索引,bitEdge是提前抽样N个可能世界后存储在边上的索引,此处N值是1000,total表示两个索引相加后的大小。可以看出索引所占的内存都较小,即使是在几十万顶点的图上,也仅要117.553 MB。
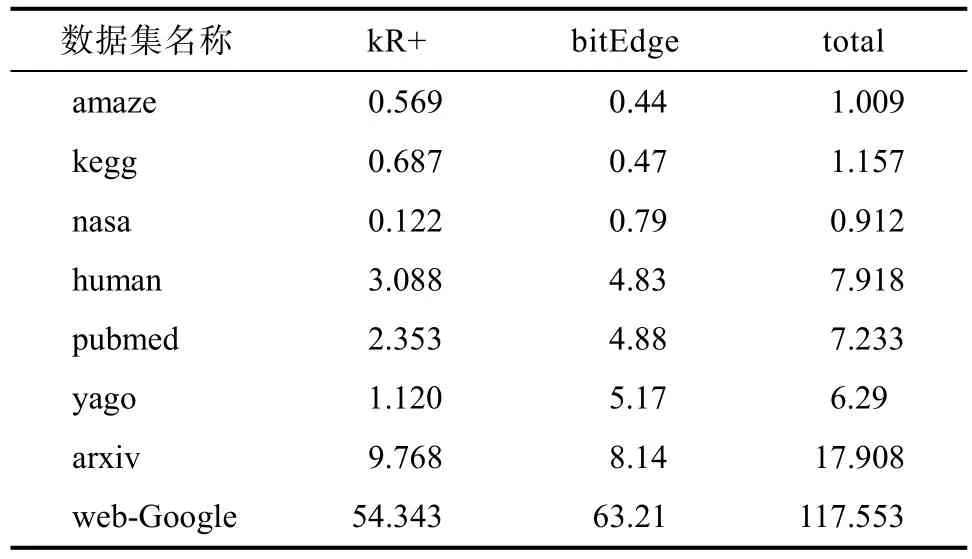
表3 索引大小/MBTab.3 Inde x Size/MB
3.3.2 索引构建时间
如表4所示,列出了构造对应索引所需的时间。在构造bitEdge位向量索引时耗时较长,因为该步骤相当于对每一条边都预先抽样了N次,优点是在后续的查询时,不论查询对是多少,都无需再进行额外的抽样,且在查询时可以直接得出结果。基于顶点覆盖构造的 kR+索引不仅消耗时间少,还能加快处理不可达查询。
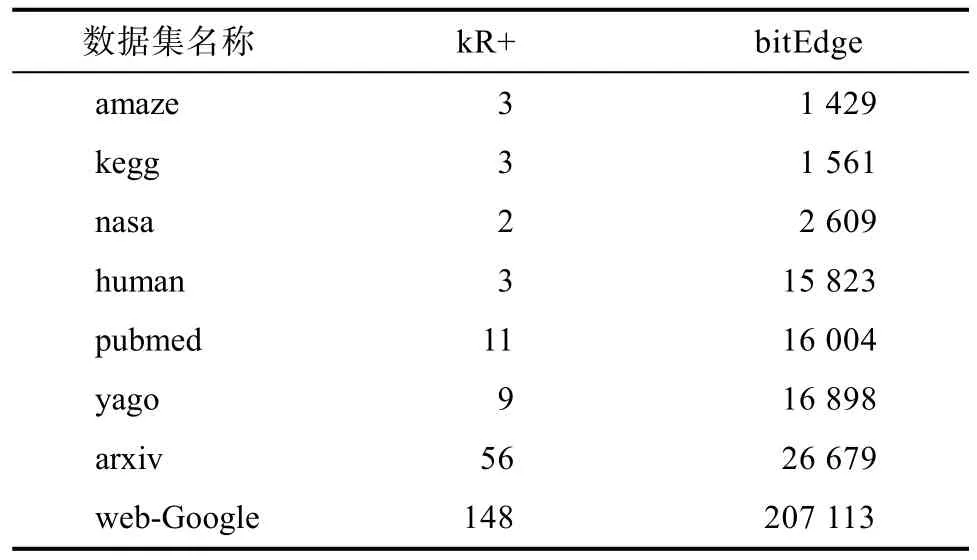
表4 索引构建时间/msTab.4 Index Building Time/ms
3.3.3 查询时间
由于朴素抽样法中,对于每一组查询对,都需要从起始点开始向外BFS寻找目标顶点,且找到后还需要判断两个顶点之间的最短距离是否满足 k步可达,消耗了极大的时间。如果u不可达v或者可达步数超过k时,更是浪费了N次的BFS遍历。
而本文提出的kRP算法先判断了查询是否满足可达和k步两个条件,又枚举出路径缩小了需要查询的边数,剪枝了不在路径上的边,查询的时候通过读取位向量就可以直接得出结果。当一条边在多次查询中用到的时候,也不需要进行重复抽样,极大地缩短了查询时间。查询100对顶点对的时间结果如表5所示,可见朴素的抽样法耗费了大量时间在冗余遍历上,只有在数据集nasa上,使用本文所提方法的构建索引时间超出了朴素方法的时间,原因是该数据集的出度较小。而其余7个数据集中,构建索引的时间都远远小于直接抽样所耗费的时间,实验结果验证了本文所提出的kRP算法的有效性。
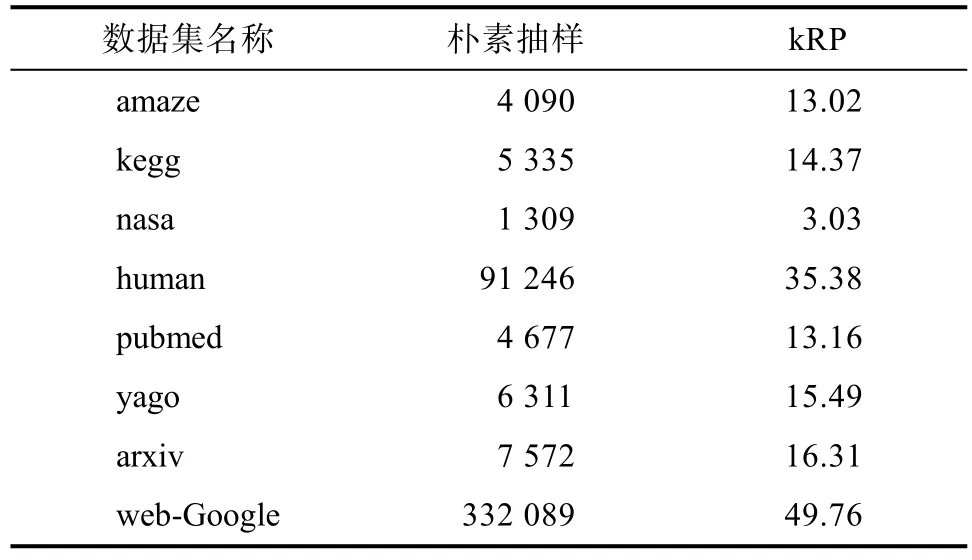
表5 查询时间/msTab.5 Query Time/ms
4 结论
本文分析了不确定图上的 k步可达近似算法,即朴素抽样的BFS方法,并针对该方法中直接抽样过于耗时的问题,提出将查询分为两种情况进行不同的处理。首先基于完全图的顶点覆盖集构建了k步可达索引,其中在求解覆盖集时按照顶点度从大到小的顺序选择顶点加入覆盖集,从而缩小覆盖集的规模。用索引判断出无法k步可达的顶点对,直接得出可达概率为 0,对这些查询不再进行后续抽样计算。对于可以k步可达的查询,本文提出基于路径来减少抽样时的边数,再用位向量的索引方式提前存储抽样图例。实验结果验证了本文所提方法的高效性。
