基于MSER-Otsu与直线矫正的仪表指针定位算法

秦 轩，冯 磊，梁庆华，张 伟

（1.上海交通大学机械与动力工程学院，上海200240；2.国家电网江苏省电力有限公司徐州供电公司，江苏徐州221000）

0 概述

随着我国经济的持续快速发展，各行各业对电力的需求不断增长，以人力为主的运维模式已不能满足实际需要，电力系统运维模式向智能化、自动化发展成为必然趋势［1］。配电站作为电力系统的末端，其运行质量直接影响用户对整体电网的满意度［2］。研发配电站无人值守作业机器人代替人工完成数据采集、处理、巡检和监控等工作，可极大程度地节约人力成本并提高运维工作效率。实现配电设备各类开关和仪表的准确识别是机器人开展配电站各项工作的基础。相较只需区分状态的指示灯和开关识别，需获取指针读数的电压表及电流表等指针式仪表的识别更复杂和困难。

指针式仪表的读数方法主要有距离法和角度法。距离法需检测指针到临近刻度线的距离，再通过刻度线的示数判断读数［3-4］。角度法需找到基准线（一般为“0”刻度线和最大值刻度线）和指针中心线，通过两两夹角的比例关系计算读数［5-6］。考虑到仪表上刻度线和刻度值较多且细小以及反光或指针遮挡会影响读数，本文采用角度法对指针式仪表进行读数。指针中心线的提取是角度法读数的主要难点和研究热点。文献［7］提出一种基于区域生长法的指针中心线提取算法，但在噪声很大时存在过分割或者欠分割问题。文献［8］利用小波变换进行边缘检测，在一定程度上可抑制图像噪声，但只适用于细指针，对于粗指针会提取出双边缘，无法实现指针中心线定位。文献［9］提出一种指针细化算法可有效解决粗指针的双边缘问题，但其只考虑指针和表盘纹理的区分，未考虑环境光照影响。文献［10］通过改进的最大稳定极值区域（Maximally Stable Extremal Region，MSER）算法和概率Hough 变换提取指针中心线并进行角度计算，但MSER 算法难以区分灰度值相近的临近区域。文献［11］通过ORB算子实现图像的倾斜矫正，再利用大律（Otsu）法和细化算法检测指针中心线，但其未考虑反光和阴影区域的干扰。文献［12］基于投票机制和轮廓圆形度思想定位表盘回转中心，进而利用指针必然通过回转中心的约束提高指针中心线检测精度，但方形指针表无法通过轮廓得到回转中心。文献［13］利用Canny 算子提取指针边缘并结合概率Hough 变换和聚类方法拟合方形指针表中指针所在直线，但其易受反光和阴影区域的影响。

由上述可知，目前国内关于指针式仪表的识别研究集中于优化指针定位方法，主要采用阈值分割结合直线检测，仅在理想的实验环境下才能实现。例如，需正对仪表拍摄且拍摄图像清晰或反光及阴影未直接影响指针，进而通过一步阈值分割分离出较为准确完整的指针区域。但在实际应用场景中，当机器人在配电站内巡检时，通常拍摄视角变化较大，且受室内位于天花板上光源的影响，表盘图像常出现较强的局部反光或阴影。由于指针在表盘上的阴影和指针非常接近，而反光可能直接遮挡指针，因此采用传统的阈值分割和直线检测方法会出现误检。

本文提出一种基于MSER-Otsu 阈值分割和矫正Hough 变换直线检测的仪表指针定位算法。利用MSER-Otsu 两步分离算法进行表盘指针区域分割，在检测指针中心线时引入Huber loss 对Hough 变换拟合直线进行矫正，并重点考虑实际场景中存在拍摄视角差异和光照等干扰时算法的可靠性，最终对配电站中方形指针表的指针中心线进行准确定位。

1 基于MSER-Otsu 的指针区域分离

1.1 预处理

指针定位的方法主要包括阈值分割和直线拟合。不同于以往研究中的圆形指针表，配电站采用的方形指针表具有细长的矩形黑色边框，会对指针提取造成干扰。因此，需对方形指针表进行预处理，如图1所示。先提取方形指针表的边框内边缘（见图1（a））并向内裁剪，得到不含黑色边框的表盘感兴趣区域（Region of Interest，ROI）（见图1（b）），然后在其中进行指针提取。在计算指针角度时，需使用边框拟合线的4 个交点进行透视变换，对图像进行倾斜矫正。

图1 方形指针表的预处理Fig.1 Preprocessing of square pointer meter

由于表盘ROI 中指针灰度值较低，因此可采用二值化方法将指针和表盘分离。考虑到表盘ROI 中除指针外还有较多的刻度线、阴影等灰度值较低区域的干扰，如果直接对整个ROI 进行阈值分割，则计算量大且难以得到较理想的结果。因此，本文采用一种先利用MSER 算法进行粗提取，然后在粗提取区域进行迭代Otsu 二值化的两步分离算法（以下称为MSER-Otsu 算法）。

1.2 MSER 算法粗提取和筛选

MSER 算法是一种利用分水岭算法思想的纹理检测方法［14］，其能检测在扫描过程中灰度值上升范围变化较小的稳定区域，具有仿射不变性，在区域检测上具有较好的性能［15］。MSER 算法的原理如下：

其中，Qi为二值图中某一个连通区域的面积，Δ为灰度阈值的微小变化量，q(i)为灰度阈值为i时连通区域面积Qi的变化率。当q(i)小于区域变化率阈值时，Qi即为最大稳定极值区域的面积，该区域随灰度值上升其面积基本不变。MSER 算法以灰度阈值i=（0，255）对图像进行扫描，对每个灰度阈值i进行图像二值化。在本文场景中，指针灰度值明显低于表盘背景灰度值且指针内部灰度均匀，符合MSER算法对检测目标的要求。

MSER 检测和筛选指针区域备选框的操作如图2所示，具体过程如下：

1）MSER 算法通过区域面积大小（设置为图像面积的0.01 倍～0.50 倍）和区域变化率阈值（设置为0.3）进行筛选。由于上述阈值设置较宽松，以确保不同拍摄条件下指针区域始终满足筛选判据，因此符合要求的备选区域较多（见图2（a）），还需进一步筛选。

2）根据指针形状和所在图像区域的先验知识，设置如下判据以选取有效的备选框（备选区域的最小外接矩形，见图2（b））：（1）指针区域备选框右侧顶点不会过于接近图像右边缘（阈值取图像宽度的5%）；（2）当备选框面积较小时（阈值取图像面积的0.1 倍），备选框形状不会过于接近正方形（长宽比范围为0.9～1.1）。

3）在返回的结果中进行一次非极大值抑制（Non-Maximum Suppression，NMS）合并重叠备选框，重叠面积阈值取0.7，保留重叠备选框中面积最大的备选框，即得到包含指针区域的单一备选框（见图2（c））。考虑到灯光照射造成反光的影响，将反光导致的异常高亮区域（见图2（d））灰度值抑制为表盘背景灰度值，此时指针出现分段，但算法仍能准确提取出包含各段指针的备选框（见图2（e））。然后仅在备选框中进行阈值分割，可极大减少干扰，提高识别效率。

图2 MSER 算法检测和筛选的指针区域备选框Fig.2 Candidate boxes of pointer area detected and filtered by MSER algorithm

为确保不漏检指针区域，筛选时阈值设置较宽松，阈值设置原则是在保证指针区域能被完整提取的前提下，尽量多地筛去干扰区域以提高识别效率，因此可能导致极少数干扰区域被保留，但保证了指针信息的完整性。

1.3 局部迭代的Otsu 算法

MSER 算法在得到备选框的同时，也会标注其中的备选区域像素点。图2（c）中备选框内备选区域像素点如图3所示。可以看出，相较于高灰度值的表盘背景，表盘示数、指针投射阴影等区域的灰度值和指针灰度值差距较小，MSER 算法会一并认为其是指针像素点。其中，阴影区域和指针十分接近，如果直接在MSER 检测的像素点中进行指针中心线提取，则会在阴影区域影响下出现结果位置偏移。因此，需进一步在MSER 提取的指针区域中进行阈值分割，以去除阴影区域的影响。

图3 MSER 算法标注的备选像素点Fig.3 Candidate pixels marked by MSER algorithm

图2（c）中含指针的备选框内存在指针像素点（灰度值最低）、阴影像素点（灰度值较低）和表盘背景像素点（灰度值最高）3 类像素点。采用固定阈值分割难以准确找到指针和阴影灰度的分界，且鲁棒性较差。使用自动计算阈值的Otsu 算法［16］仅能将区域分为两类，由于表盘白色背景像素点数量较多且灰度值较高，单次Otsu 算法易误将指针和阴影归为同一类，这显然不符合分离指针的要求。

本文目标是将指针和临近阴影分开，为解决这一问题，通过结合灰度级扩展的两轮迭代Otsu 算法实现图2（c）中3 类像素点的分割（见图4），该算法具体步骤如下：

图4 局部迭代的Otsu 算法分离指针过程Fig.4 Pointer separating process by local iterative Otsu algorithm

1）将表盘ROI 中除备选框外的其他区域像素点灰度值设置为0。

2）选取一个备选框内全部像素点，记为备选点集。

3）在备选点集中进行Otsu 阈值分割，将表盘背景和其他区域（包括指针和阴影）像素点分开，并标记超过阈值的像素点。

4）在备选点集中剔除超过阈值的像素点，在剩下的像素点中将灰度级扩展到［0，255］，再次进行Otsu 阈值分割，即可将该备选框内指针和阴影分开。

5）选取下一个备选框，重复步骤2～步骤4，直到完成所有备选框的阈值分割，即完成整个表盘ROI的阈值分割。

由灰度直方图分析可知，图4（a）备选框内主要有指针和刻度像素点、阴影像素点以及白色背景像素点3 类像素点，其灰度值范围分别为0～60、80～110和130～160。第一轮Otsu 算法分割计算出灰度阈值为106，因此将灰度值在80～106 范围内的阴影像素点和指针像素点归为一类，造成阴影和指针的粘连（见图4（b））。剔除超过阈值的像素点并进行灰度级扩展后，备选框内主要剩余指针和刻度像素点、被误分的阴影像素点两类像素点，其灰度值范围分别为0～144和192～255。第二轮Otsu 算法分割计算出灰度阈值为146，可将指针和阴影分开（见图4（c））。在一般情况下，接近该类像素灰度值边界的极少数像素点可能会被误分割，但其对结果的影响可忽略。

2 基于直线矫正的指针中心线提取

经过上述处理后，可获得仅含指针像素点和极少量干扰（包括MSER 算法误检区域和正确备选框内未筛去的刻度线等）的表盘ROI 二值化图像。对于本文所研究方形指针表内的粗指针，还需进一步提取单像素的指针中心线以计算指针偏转角度。提取粗指针中心线的常见方法有指针形态学细化结合Hough 变换［9-11］。但指针形态学细化的过程需要设计复杂的迭代筛选条件且耗时较长（见本文第3.2节）。因此，本文设计一种基于直线检测与矫正的指针中心线提取方案以提高处理效率。

2.1 Hough 变换预定位

在表盘ROI 二值化图像中，指针像素点均近似位于一条直线附近，可通过Hough 变换进行检测。考虑到反光区域可能将指针分为两段（见图2（d）），本文采用基础Hough 变换检测直线而非线段，从而同时利用多段指针信息，返回累加值最高的直线即为近似的指针中心线。

Hough 变换通过离散化的直线参数进行搜索，其精度与搜索步长一致。受限于算法时间复杂度，精度和搜索步长分别为1°和1 像素。此外，由于指针有一定宽度，而Hough 变换的结果（直线）仅考虑直接经过的像素点，并不完全贴合指针中心线，需对其进行矫正，以下介绍本文采用的矫正算法。

2.2 Huber loss 直线矫正

以Hough 变换得到的直线为基准线，记为L0(ρ0,θ0)，利用二值图中临近基准线的像素点对基准线进行矫正。设临近基准线的像素点集合为P，其表达式如下：

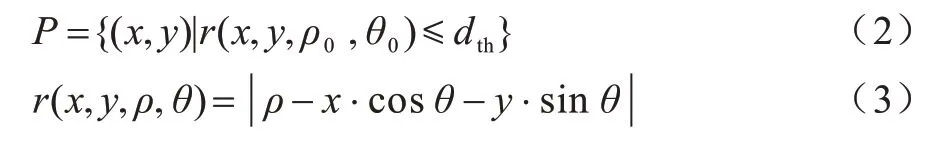
由于本文输入图像的大小在一定范围内，因此考虑指针宽度，dth取5 像素，从而在包含临近指针像素点的同时排除其他区域干扰。

设矫正直线为Lnew(ρ,θ)，以下求取最优参数(ρ,θ)，使P中像素点到Lnew(ρ,θ)的距离总和最小，计算公式如下：

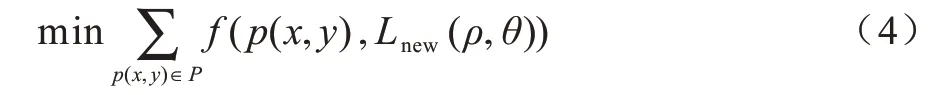
式（4）是一个回归问题，通常使用最小二乘法求解。考虑到最小二乘法采用均方误差（Mean Squared Error，MSE）容易受离群噪声点影响［17］，因此，本文采用Huber loss［18］作为最优化函数，计算公式如下：

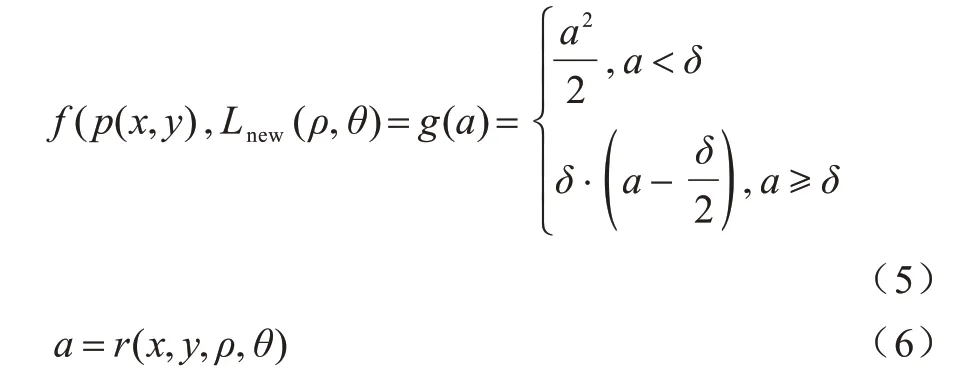
Huber loss 在像素点距离直线较近时采用均方误差，收敛较快，其在像素点距离直线较远时采用平均绝对误差（Mean Absolute Error，MAE），受离群噪声点影响比均方误差小［19］，距离阈值δ=0.5dth=2.5，采用梯度下降法进行迭代计算直至收敛。上述方法所得指针中心线提取结果如图5所示。

图5 指针中心线提取结果Fig.5 Extraction result of center line of pointer

2.3 指针角度计算

提取到指针中心线后，利用预处理所得表盘内边框4 个顶点向正方形4 个顶点做透视变换，将图像矫正为正视图，此时指针中心线和图像下边缘的夹角即为方形指针表的指针角度。

3 实验与结果分析

使用Python 3 编程语言和OpenCV 库编写程序验证本文提出的MSER-Otsu 算法（以下称为本文MSER-Otsu 算法）的效果。实验采用Ubuntu 16.04 64 位系统，16 GB 内存以及2.80 GHz CPU。

3.1 指针区域分离

在指针区域分离方面，针对图2（c）和图2（e）中两类情况，将单次Otsu 算法、全图两轮迭代Otsu 算法、MSER 算法与本文MSER-Otsu 算法的二值化图像分割情况进行对比，结果分别如图6 和图7所示。

图6 不同算法得到的图2（c）中指针区域分离结果Fig.6 Results of pointer region separation in Fig.2（c）obtained by different algorithms

图7 不同算法得到的图2（e）中指针区域分离结果Fig.7 Results of pointer region separation in Fig.2（e）obtained by different algorithms

由图6 和图7 可以看出，单次Otsu 算法和MSER算法均无法分离指针和阴影、纹理等灰度相近的区域。全图两轮迭代Otsu 算法尽管可以分离指针和阴影区域，但会在其他区域留下许多干扰点（如文字、刻度线和右下角阴影等）。本文MSER-Otsu 算法利用MSER 算法粗提取检测备选框，在备选框外完全无干扰点，且在备选框内利用两轮迭代Otsu 算法对3 类像素点进行阈值分割，成功完成指针和阴影像素点的分离。

全图两轮迭代Otsu 算法和本文MSER-Otsu 算法的时间开销如表1所示。由于本文MSER-Otsu 算法是在备选框局部进行迭代，较全图两轮迭代Otsu算法所用时间开销更小，识别效率更高。

表1 两种算法分离指针区域的时间开销对比Table 1 Comparison of time cost for pointer region separation between two algorithms ms

3.2 指针中心线提取

本文采用Huber loss 矫正和Hough 变换的算法（以下称为本文矫正Hough 变换算法）进行指针中心线提取。针对图6（d）和图7（d）中两类情况，将仅使用Hough 变换算法、直接Huber loss 拟合算法、指针细化算法结合Hough 变换算法（以下称为ZHANG细化结合Hough 变换算法，其中指针细化算法为经典的快速并行ZHANG 细化算法［10，20-21］）和本文矫正Hough 变换算法的效果进行对比，结果分别如图8 和图9所示。

图8 不同算法得到的图6（d）内指针中心线提取结果Fig.8 Results of pointer center line extraction in Fig.6（d）obtained by different algorithms

图9 不同算法得到的图7（d）内指针中心线提取结果Fig.9 Results of pointer center line extraction in Fig.7（d）obtained by different algorithms

通常情况下指针较完整（见图8），由图8可以看出，仅使用Hough 变换算法所得结果贴近指针上边缘，偏离指针中心线，这是由于Hough 变换算法只考虑单条直线通过的像素点数量，未考虑粗指针上其他像素点信息导致。直接使用Huber loss 对二值图中全部有效像素点进行拟合会受其他噪点干扰（如刻度、右下三角区域和指针尾部轮廓），结果明显偏离指针中心线。ZHANG 细化算法首先提取指针骨架，再对骨架进行Hough 变换，所得结果基本与指针中心线重合。本文矫正Huber loss 变换算法将Hough 变换临近的指针像素点全部纳入考虑范围，使其到矫正直线的距离最小，同时因为指针关于其中心线对称，所以矫正直线就是指针中心线的近似直线。此外，相较于在全图使用Huber loss拟合算法，本文矫正Huber loss变换算法采用Hough变换预定位，只计算预定位直线临近的像素点，排除了大部分干扰像素点，因此结果明显优于直接拟合。极端情况下受反光影响，二值图中指针较细且靠右侧上边缘有所缺失（见图9）。由图9 可以看出，各算法所得结果均偏向指针下边缘，本文矫正Hough 变换算法通过引入预定位直线临近像素点做整体拟合，提取的直线在所有算法中距离指针下边缘最远，且指针在直线两侧的像素数量变化较一致，与指针中心线重合度最高。

ZHANG 细化结合Hough 变换算法所得结果和本文矫正Hough 变换算法相近，但其细化处理非常繁琐，计算效率较低，时间复杂度为O（k1n+c），其中n为备选框内像素点总数（即备选框面积），k1为细化算法单个像素点处理计算量（k1较大），c为Hough 变换时间复杂度。本文矫正Hough变换算法时间复杂度为O（k2m+c），其中m为Hough 变换直线临近的指针像素点数，k2为梯度下降迭代处理计算量。由上述可知，m明显小于n，而由于候选点在一条直线附近，梯度收敛很快，k2较小，因此O（k2m）＜O（k1n）。两种算法中Hough 变换顺序不同，导致候选点数量不同，效率上有一定差异，但相对于ZHANG 细化算法的处理时间，该耗时可忽略，因此O（k2m+c）＜O（k1n+c）。

将图像进行缩放，限制表盘ROI图像长度和宽度均约为200 像素，此时含指针的备选框长度和宽度范围为50 像素～150 像素，二值图中分割出指针像素点数约为200（反光造成部分指针被遮挡的情况下）～1 000。图8和图9中两种算法拟合出指针中心线的时间开销如表2所示。由表2 可见，本文矫正Hough 变换算法提取指针中心线的时间开销较ZHANG 细化结合Hough 变换算法更小，识别效率更高。对于实际图像中像素点范围为200～1 000 的指针，本文矫正Hough 变换算法的时间开销均约10 ms，具有良好的实时性。

表2 两种算法提取指针中心线的时间开销对比Table 2 Comparison of time cost for extracting pointer center line between two algorithms ms

3.3 配电站实际应用

在配电站实际应用中，本文算法对于不同外观的方形指针表、不同拍摄视角、光照和阴影干扰均有较强鲁棒性，在本文选用的75 张图像中，指针定位成功率达到100%，部分定位效果如图10所示。

图10 不同情况下指针定位效果图Fig.10 Effect images of pointer positioning in different situations

由于配电站的指针式仪表的表盘刻度不均匀，且仪表型号各有不同，因此统一采用指针角度值进行比较，将现场人工测量指针和下边框的实际夹角作为真实值，采用本文算法得到的指针角度值从小到大随机选取10 组，结果如表3所示。由表3 可见，本文算法计算结果和人工测量真实值最大绝对误差为1.00°，平均绝对误差为0.52°，相对全量程（90.00°）的最大相对误差为1.1%，平均相对误差为0.6%。考虑到人工测量的最小精度为0.50°，本文算法的识别精度已满足实际应用要求。

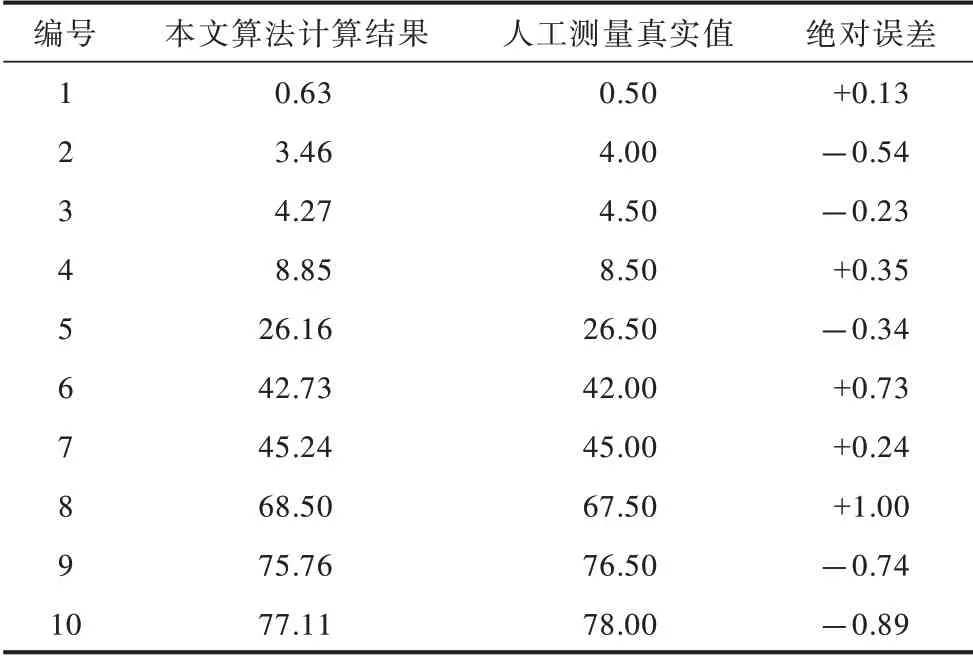
表3 本文算法和人工测量得到的仪表指针角度值Table 3 Angle values of meter pointer obtained by the proposed algorithm and manual measurement (°)

4 结束语

针对配电站巡检机器人难以识读方形指针式仪表的问题，本文提出一种仪表指针定位算法。采用MSER-Otsu 两步分离算法分割出表盘指针区域，利用Huber loss 矫正Hough 变换拟合直线，最终完成指针中心线的检测。实验结果表明，与Hough 变化算法和Huber loss 拟合算法等相比，该算法处理速度更快且鲁棒性更高，其能在不同拍摄视角和光照干扰下对多种方形指针表的指针进行准确定位。但本文算法在备选框较大时背景点去除和灰度级扩展的耗时明显增加，考虑到Otsu 分割耗时很短，本文局部Otsu 迭代效率还有很大提升空间，后续将对此进行优化，进一步提高巡检机器人识读指针式仪表的实时性。