室内环境下无线干涉定位系统的多径误差分析

金彦亮，王 妍，齐 崎，唐晨君，刘千红

（上海大学通信与信息工程学院，上海200444）

0 概述

节点位置信息是无线传感器网络（Wireless Sensor Network，WSN）所需要的基本信息［1-2］。目前比较常用的节点定位方法RSSI［3］、TOA［4］、TDOA［5］和AOA［6］，都是利用节点之间的距离和角度来实现定位。TDOA、TOF［7］和AOA 定位精度较高，但同时对硬件也有较高的要求，在信号处理、通信和能量等方面的代价也较高［7-9］。无线干涉定位系统（Radio Interferometric Positioning System，RIPS）基于易于获得的RSSI 信号，其优点在于系统部署简单、硬件代价低，是一种低成本和具有高精度潜力的定位方法［10］。为提高节点定位性能，文献［10-12］从不同角度对RIPS 进行了改进。但在实际应用中，RIPS 的室内定位效果远不如在室外的定位效果，这是因为相较于室外的空旷环境，室内的陈设和空间比较复杂，墙壁和物品导致的复杂多径反射使得节点接收到的包络信号存在严重的相位偏差［13］。因此，多径效应是RIPS 应用于室内环境必须要解决的问题［14］。为避免多径效应，可以对RIPS 进行一系列优化，如调整天线、降低载波频率、增设冗余节点等［1，15-17］。然而，这些优化方法在解决多径效应问题的同时也带来了较高的硬件成本。

在多径室内环境下进行节点定位，存在实测测距误差远大于仿真误差的问题。本文结合RIPS 算法和多径修正算法搭建硬件平台和仿真系统进行实验，分别从采样方式、反射系数和节点高度3 个方面分析产生误差的原因，并提出有效的修正方法。

1 无线干涉定位系统模型

1.1 无线干涉定位算法

无线干涉定位系统（RIPS）可实现无线传感器网络中精确的节点定位。RIPS 的节点布局通常采用“双发双收”的模式，即先测量两个接收节点处的干涉信号并获取信号包络的相位，再对这两个接收节点的相位作差进行定位。系统中的节点分布如图1所示，其中，A、B 节点发射多组频率相近的载波信号，C、D 作为接收节点，A、B、C 的位置已知，D 为待定位节点［18］。

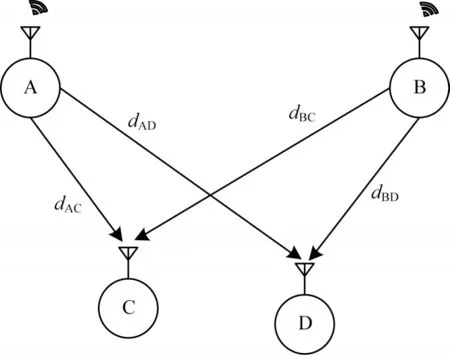
图1 无线干涉定位系统节点分布Fig.1 Node distribution of RIPS

发射节点A、B 同时发射频率相近的高频未调制正弦信号，在接收节点C、D 处产生干涉。RIPS 采集到干涉信号的包络，得到各节点包络信号的相位并进行求差运算［19］。相位差和待定位节点位置的关系如式（1）所示：

其中，φABCD(f)为两节点间的相对相位差φC-φD，可以通过测量得到，dAC、dBC、dAD、dBD分别表示各个节点之间的直线距离，dAC和dBC已知，c表示光速，f为两个发射节点发射的载波信号频率的均值(fA+fB)/2，λ为载波信号波长，即。dABCD=dAD-dBD+dBC-dAC的值与φABCD(f)相关。由于存在求模运算，因此φABCD(f)的值存在模糊解。为解决模糊解的问题，可通过发射节点发射多组频率不同的载波信号来进行多组相位差的测量，从而计算dABCD以消除模糊解。根据dABCD的值同时结合A、B、C 点的坐标，可以得到估算的D 点坐标。

1.2 多径效应误差模型

RIPS 应用于室内环境时会受到多径效应的严重干扰。从信号传播的角度考虑，多径分析可以采用信号强度叠加的空间内矢量关系方法。N径误差信号的矢量关系可以抽象为图2所示模型。

图2 N 径误差信号矢量关系模型Fig.2 Signal vector relationship model of N-path error model

以X 表示发射节点，Y 表示接收节点，则X 发Y 收的多径相位偏差可表示为：

其中，SdXY为从发射节点X 到接收节点Y 的直达径的信号强度，SrXY,i为反射径i的信号强度，θXY,i为反射径i与直达径信号的相位偏差。SrXY,i由反射面的反射系数决定，θXY,i由节点间的距离、反射径的距离和载波频率决定。

接收节点C 绝对相位的多径偏差为：

由于C 点位置坐标已知，φAC和φBC可以由式（2）得到，因此将Δφ作为误差修正项可以实现室内场景下RIPS 定位的多径修正。

1.3 仿真与实测结果

为验证无线干涉定位算法的测距效果和多径修正算法的修正效果，搭建仿真模型和硬件平台对定位效果进行仿真和实测。

定位实验设置5 个节点，其中包含2 个发射节点、2 个接收节点和1 个协调节点，协调节点用于同步发射节点信号的发射，发射的载波频率在2.4 GHz 的频段，频率间隔为5 MHz，共16 组频率。系统进行一次定位需要两轮测量，两轮测试的测量方案如表1所示。

表1 室内测量方案Table 1 Indoor measurement scheme in indoor enviroment

在MATLAB 中建立5 m×11.1 m×8 m 的室内模型，将多径数目设为3（N=3），考虑直达径、天花板反射径和地面反射径3 条主径的情况，仿真时预设已知真实的反射系数，并假设天花板反射径和地面反射径的反射系数均为0.5。节点位置参数和各参数设置如表2所示，除协调节点外，其余的节点高度均设置为1 m。

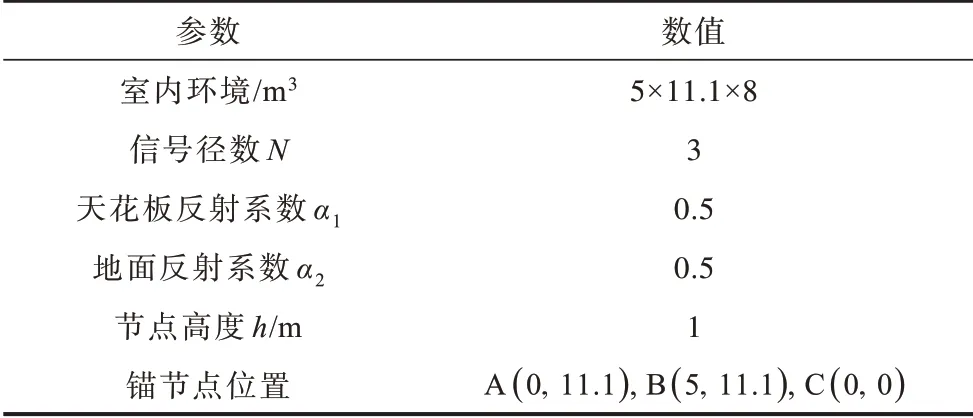
表2 参数设置Table 2 Parameters setting

硬件平台基于CC2530 芯片天线组成，每个CC2530 芯片连接一个天线作为一个节点，定位环境设在一个5×11.1×8 m3空旷大厅，假定天花板和地面反射系数分别为0.7 和0.6。节点高度、锚节点位置和载波频率采用前述仿真设置。

统计10 次实测结果得到测距平均定位误差为2.92 m。相位校正后，定位误差降为2.80 m，定位误差缩小了4.1%。

在仿真中，统计100 次相位校正前的定位误差，得到平均定位误差为0.43 m。对100 个随机位置进行相位校正，经过校正后，平均定位误差降为0.26 m，相位校正后平均定位误差比相位校正前下降了39.53%，这说明在仿真条件下，使用三径误差模型进行相位校正能够有效提高定位精度。

对比实测结果和仿真结果可以看出：实测平均误差较大，为2.92 m，相位校正后可减少0.12 m；仿真平均误差为0.43 m，相位校正后可减少0.17 m。由此可见，室内多径环境下RIPS 算法实测结果和仿真结果存在较大的误差，下文将对此进行详细分析。

2 系统误差分析

2.1 信号采样方式

本节分析信号采样方式对定位结果的影响。在实测系统中，接收节点以62.5 kHz 的采样率对干涉信号采样，采集200 个RSSI 信号点作为包络信号。但被采样的信号不是真实的包络信号而是高频载波信号，这样的采样方式会使采集到的包络信号存在一定程度的相位偏移。

为研究采样方式和定位误差的关系，本文设定3种采样方式，即采样率为62.5 kHz、125 kHz 和通过每2 000 个干涉信号取信号最大值来模拟经过低通滤波后的干涉信号（干涉信号包络），并对3 种情况分别进行仿真。仿真环境参数设置见表2。设D 为待定位节点，其位置为100个随机位置的节点。测量方案见表1。

由图3 可以看出，使用接收信号的理想包络来测距的误差显著小于直接对干涉信号进行高频采样的误差。从该图中还可以看出，62.5 kHz 采样和125 kHz 采样下的测距误差曲线几乎完全重合，这说明当采样频率足够时，再提升采样频率也不能提高定位精度。

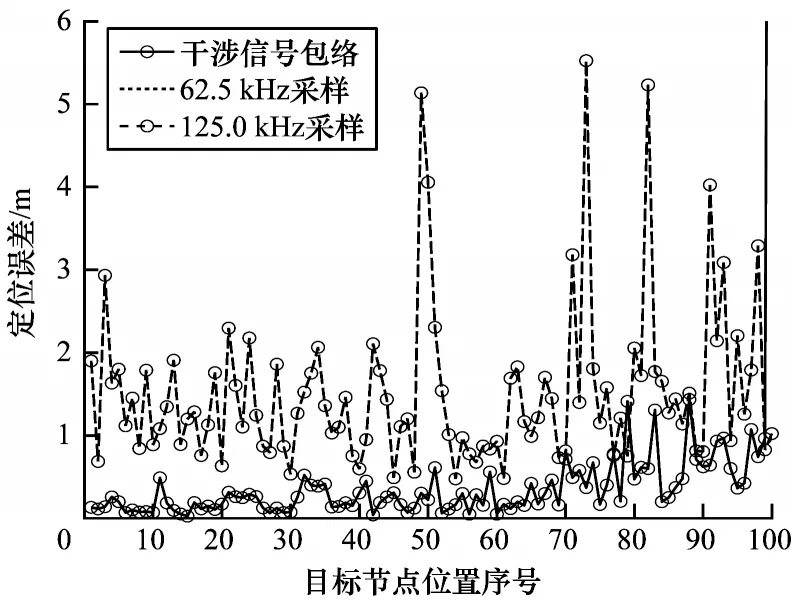
图3 不同采样方式下的定位误差Fig.3 Positioning errors under different sampling modes

2.2 反射系数与节点高度

本节分析反射系数α1、α2和节点高度h对定位误差的影响。在实测定位中，由于反射系数根据经验选取，因此可能与实际反射系数不同而引入误差。

采用与上文相同的仿真环境。假设天花板和地面的反射系数相同，将节点高度h设置为1 m，代入不同的反射系数，得出不同反射系数下100 个随机位置的待定位节点对应的平均定位误差，如图4所示。可以看出，随着反射系数的变化，定位误差产生了跳变，这是因为在仿真环境的节点空间布局下，节点到反射面的距离过近，导致在使用多径算法修正时，相位产生了溢出，表现在定位结果上即定位误差随反射系数的变化而产生跳变。因此，需要通过改变节点高度进行修正。

图4 不同反射系数下的定位误差（h=1 m）Fig.4 Positioning error under different reflection coefficients（h=1 m）

在仿真条件中，将节点高度h调整为2 m，其他参数保持不变，使用表2 的测量方案进行第2 次仿真，仿真结果如图5所示。可以看出，改变节点的空间布局能够有效防止相位溢出和误差剧增。

图5 不同反射系数下的定位误差（h=2 m）Fig.5 Positioning error under different reflection coefficients（h=2 m）

2.3 实验结果

通过仿真实验验证节点高度、反射系数和采样方式这三个方面对RIPS 测距结果的修正效果。

对干涉信号直接采样，使用错误的反射系数（仿真中取0.6），并设置节点高度为1 m，获取第1 轮仿真结果，同时单独修正采样方式、反射系数和节点高度，进行第2 轮～第4 轮仿真。第5 轮～第7 轮仿真分别分析了仅使用错误的采样方式、错误的反射系数或节点高度为1 m 时引入的误差。最后，令节点高度为2 m，反射系数采用0.5，采样方式为滤波后采样，其他仿真条件不变，进行第8 轮仿真。每轮仿真测量100 个随机位置的节点，得到平均定位误差，如表3所示。可以看出，在对含高频的干涉信号直接采样、采用不正确的反射系数并设置节点高度为1 m 的情况下，测距误差为2.8 m。第2轮～第4轮仿真结果显示，仅修正采样方式、反射系数或节点高度分别可以降低1.02 m、0.29 m 和1.01 m 的误差。第5 轮～第7 轮仿真结果显示，在其他条件理想的情况下，使用直接采样、错误的反射系数或设置节点高度为1 m，测距的误差分别为1.54 m、0.61 m和1.54 m。第8 轮仿真结果显示，修正后的平均定位误差降低到0.36 m。

表3 8 轮仿真实验的定位结果Table 3 Positioning results of eight rounds of simulation experiments

仿真结果表明，通过提高节点高度、改正反射系数和滤波后采样的方法能够有效降低实测中的测距误差，经过修正后，仿真与实际的偏差缩小了87.61%。因此，使用硬件平台进行实测时，可以通过在接收节点前加低通滤波器的方式来减小包络的相位偏差，并通过提升节点高度的方式避免测距过程中相位溢出的情况。文献［20］也提出了在定位之前发射测试信号来对反射系数进行实测的方法，同样提升了测距精度。

3 结束语

本文针对无线干涉定位系统在多径环境下实际测量与理论仿真误差相差较大的问题，通过建立仿真模型，分别分析采样方式、反射系数和节点高度3 个因素对测距误差的影响。仿真结果表明，节点距离地面较低或不加滤波直接对干涉信号进行采样是实测过程中造成误差的主要原因，经过修正后，理论上实测定位误差较仿真误差可降低87.61%。下一步拟将理论误差修正方法应用于实测定位中，并结合具体需求优化无线干涉定位系统。