罕遇地震作用下钢筋混凝土框架结构韧性评价

杨圆月，杨青顺

(青海大学土木工程学院，青海省建筑节能材料与工程安全重点实验室，青海 西宁 810016)

传统的结构防震减灾是为了确保在地震灾害来临时建筑物内人员的生命安全不受到威胁，但随着现代化城市建筑体系复杂多样，简单地保证建筑结构能承受地震作用而不发生倒塌破坏已经不能满足人们对建筑物抗震性能的要求。现代化城市中的公共建筑承担着让整个城市稳定运行的特殊功能，如学校、医院、电力公司、政府机关等，对于这样的公共建筑，按照抗震设计规范的要求仅去抵御地震造成的破坏是不够的，这些建筑设施都需要在震后实现快速恢复。因此，相较于基于规范的抗震设计和基于性能设计的方法，基于韧性的抗震设计受到了越来越多的关注。近年来国内外对于韧性城市的研究愈渐深入[1-3]，城市抗震韧性的概念也得以推广。目前已有不少学者对地震后各系统设施展开了韧性研究，如费智涛等[4]以复杂性系统为前提，提出了反映该系统韧性能力的5项指标，并对北京某地区的医疗系统进行了韧性评价；李雪等[5]建立了海岛综合能源系统的数学模型，以鲁棒性、快速性和冗余性3个维度来衡量海岛能源系统韧性的优良性，并利用该方法对巴厘岛综合能源系统进行了韧性评价；李岩峰等[6]利用投影寻踪方法建立了供水管网的理论模型,数据化表达了供水管网在地震时的韧性能力,划分了各管段在地震作用下的韧性等级，并利用该方法评估了某供水管网。然而，这些研究都是以医疗系统、能源系统、供水系统等为研究对象，对于系统的韧性评价是宏观的，目前鲜有针对具体的建筑进行韧性评价的分析和研究。本文拟建立钢筋混凝土框架结构在罕遇地震作用下的有限元模型，通过构件相对转角以及楼层的最大响应得到框架结构中梁柱的损伤情况和非结构构件的损伤情况，以构件的损伤数据为依据提出了一种关于功能损失及恢复时间的计算方法，总结影响该结构韧性能力的关键因素。

1 结构模型及参数

1.1计算模型本文以一个简单的6层框架结构为例，该结构层高均为3.6 m，总高21.6 m，开间大小为5 m×5 m，平面尺寸为15 m×10 m，平面布置如图1所示。该框架结构抗震设防烈度为 7度(0.3 g)，场地类别为二类，框架抗震等级为二级，抗震分组为第3组。

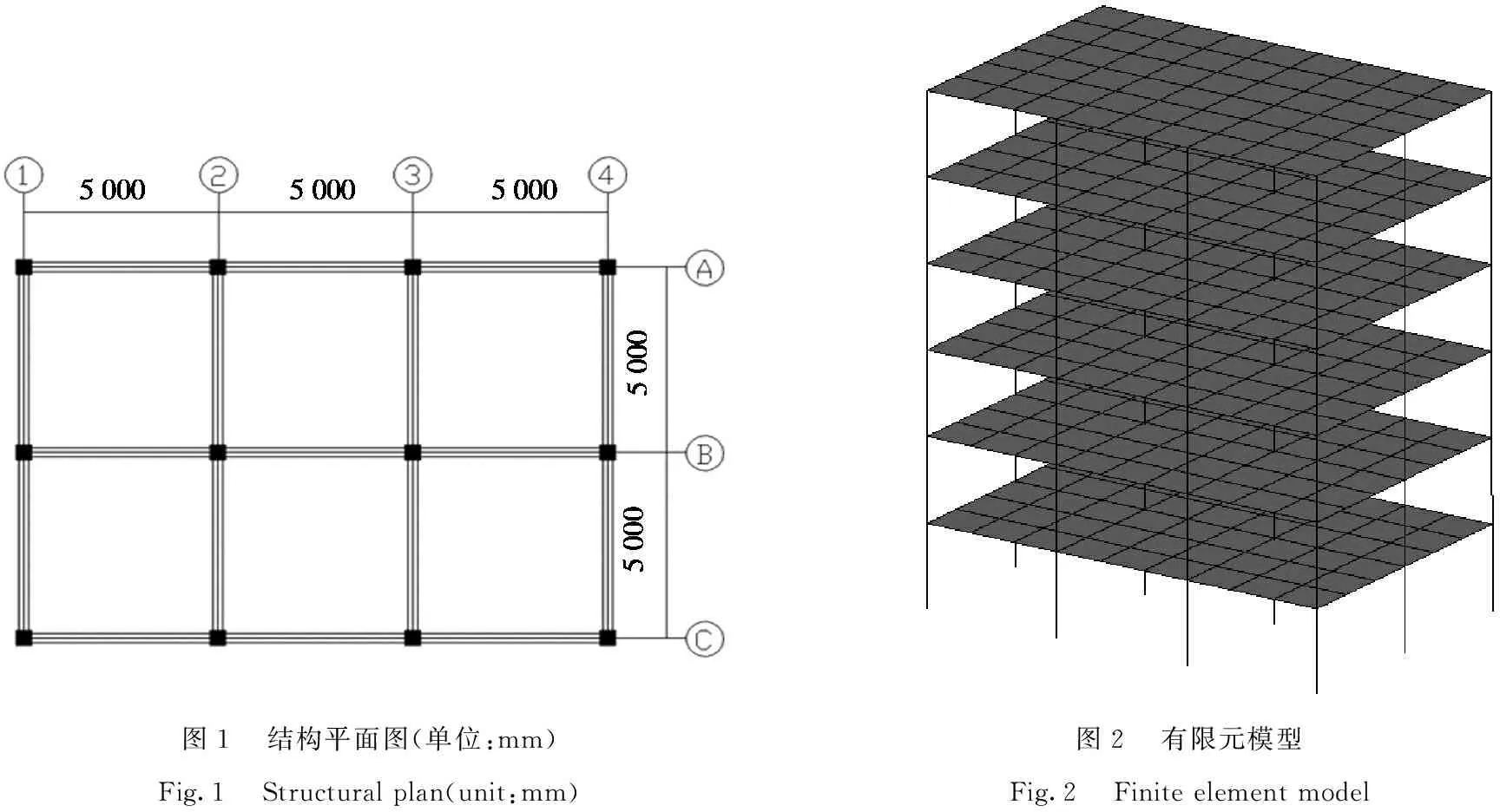
图1结构平面图(单位:mm)Fig.1Structural plan(unit:mm)图2有限元模型Fig.2Finite element model

梁柱楼板所使用的混凝土均为C30，弹性模量为3×104N/mm2，抗压强度为30 MPa，峰值压应变为0.002；纵向钢筋为HRB400，弹性模量为2×105N/mm2，屈服强度为400 MPa。梁的截面尺寸都是0.25 m×0.7 m，第1层到第3层柱的截面尺寸为0.5 m×0.5 m，第4层到第6层柱的截面尺寸为0.4 m×0.4 m，楼板的厚度为0.1 m。因在THUFIBER[7]中输入的信息为材料的标准值，故混凝土和钢筋材料参数按规范采取对应的标准值[8]，梁上的隔墙线荷载由隔墙重量等效计算得到，为5 kN/m，楼板的恒荷载为5 kN/m2，活载为2 kN/m2。根据PKPM设计结果，采用具有良好可二次开发性的有限元软件MSC.Marc为建模平台，建立了框架结构的有限元模型(图2)。建模的基本方法如下：

(1)为了对框架结构的非线性弹塑性进行分析，混凝土梁柱材料本构模型采用的是陆新征等[7]开发的基于MSC.Marc、Fortran 纤维梁柱单元THUFIBER程序进行模拟[7]，MSC.Marc中采用98号单元。

(2)本结构将进行大震弹塑性分析，楼板采用的是分层壳模型，楼板单元采用139号单元[8]。

(3)为了方便荷载在有限元软件中的输入，对于结构所受荷载，将梁上的隔墙等效线荷载和楼板上恒载和活载折算为相应的梁和楼板的密度进行模拟计算。重力荷载代表值按规范取为1倍恒载加0.5倍活载[9]。

1.2模型验证利用有限元软件MSC.Marc建立模型后，为了保证有限元模型的合理性，需进行相应的模型验证工作。将模型计算结果与PKPM设计结果进行周期和结构总质量的比较，对比的结果如表1和表2所示。

表1 模型质量检验Tab.1 Quality inspection of the model

表2 模型周期检验Tab.2 Periodic inspection of the model

由表1和表2可以看出，模型的重力检验结果误差为2.5%，说明建立的模型与实际结构较为吻合。模型在平动周期上的误差均小于7%，有限元模型动力特性符合要求[6]。

2 罕遇地震下的动力时程分析

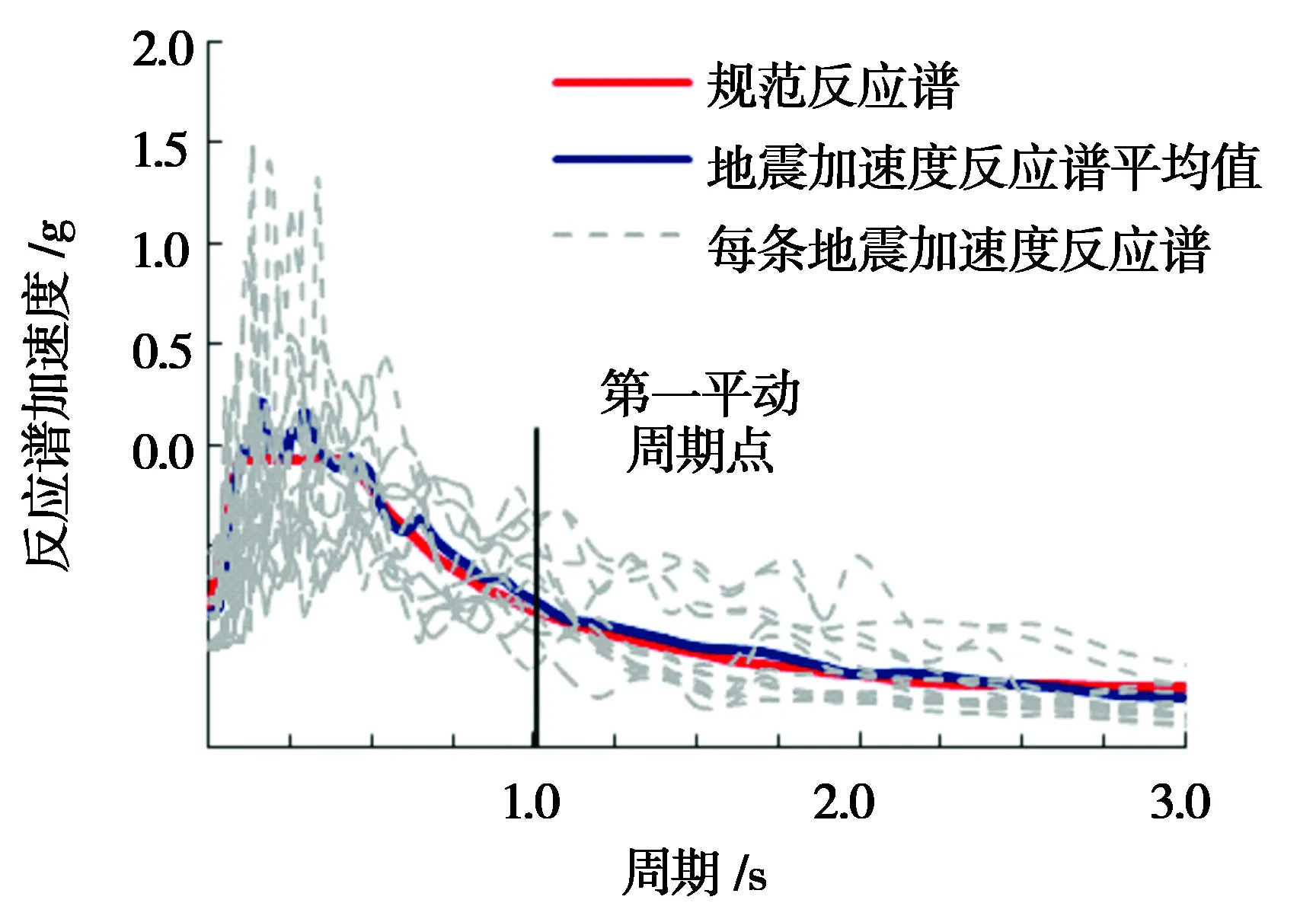
图3 地震加速度时程曲线Fig.3 History curve of seismic acceleration

2.1地震动的选取根据GB 50011—2016《建筑抗震设计规范》[8]的规定，由目标反应谱在太平洋地震工程研究中心(PEER)NGA-West 2数据库选取了11条地震动记录，并且地震加速度反应谱平均值与规范反应谱在第1平动周期点的相对误差不大,为15%(图3)，将地震峰值加速度(PGA)调幅至7度(0.3 g)罕遇地震所对应的值，即310 m/s2。按照GB/T 38691—2020《建筑抗震韧性评价标准》[9]三向输入地震动记录时，比例为x:y:z=1∶0.85∶0.65。本文采用经典的阻尼取法，假设结构的阻尼为质量比例型，结构各阶振型阻尼比均相同，混凝土框架结构的可取ζ=0.05。

2.2楼层响应在MSC.Marc中选取11条地震动进行动力时程分析，利用Python软件提取楼层各单元节点的加速度和位移数据。加速度选取在动力时程分析中所有增量步数据绝对值的最大值，层间位移角由相邻楼层对应节点的绝对位移除以层高获得，得到结构楼层的最大响应(图4为楼层加速度，图5为层间位移角)。

图4楼层加速度Fig.4Floor acceleration图5层间位移角Fig.5Interlayer displacement angle

由图4可以看出，11条地震动得出的加速度数据整体浮动平稳，1～3层随着楼层高度的增加，加速度在不断变大，到第4层时因柱构件截面尺寸变小而导致刚度突变，加速度有所下降，但4～6层仍呈上升趋势。此外，由图5可知，在大震弹塑性分析的情况下，结构的薄弱层为第4层，其层间位移角相较于其他楼层偏大，顶部的位移角最小，且最大位移角满足规范中所规定的弹塑性层间位移角限值(0.022)[10]。

2.3损伤状态对结构进行弹塑性时程分析后，使用编程软件Python提取数据，对于框架结构而言，工程需求参数包括结构的层间位移角、楼面绝对加速度、梁柱构件相对转角，结合结构构件和非结构构件的易损性数据库，采用蒙特卡洛模拟及易损性曲线超越概率的方法确定全部构件的损伤状态[8]。梁的损伤状态如图6所示，柱的损伤状态如图7所示，非结构构件的损伤状态由图8所示。

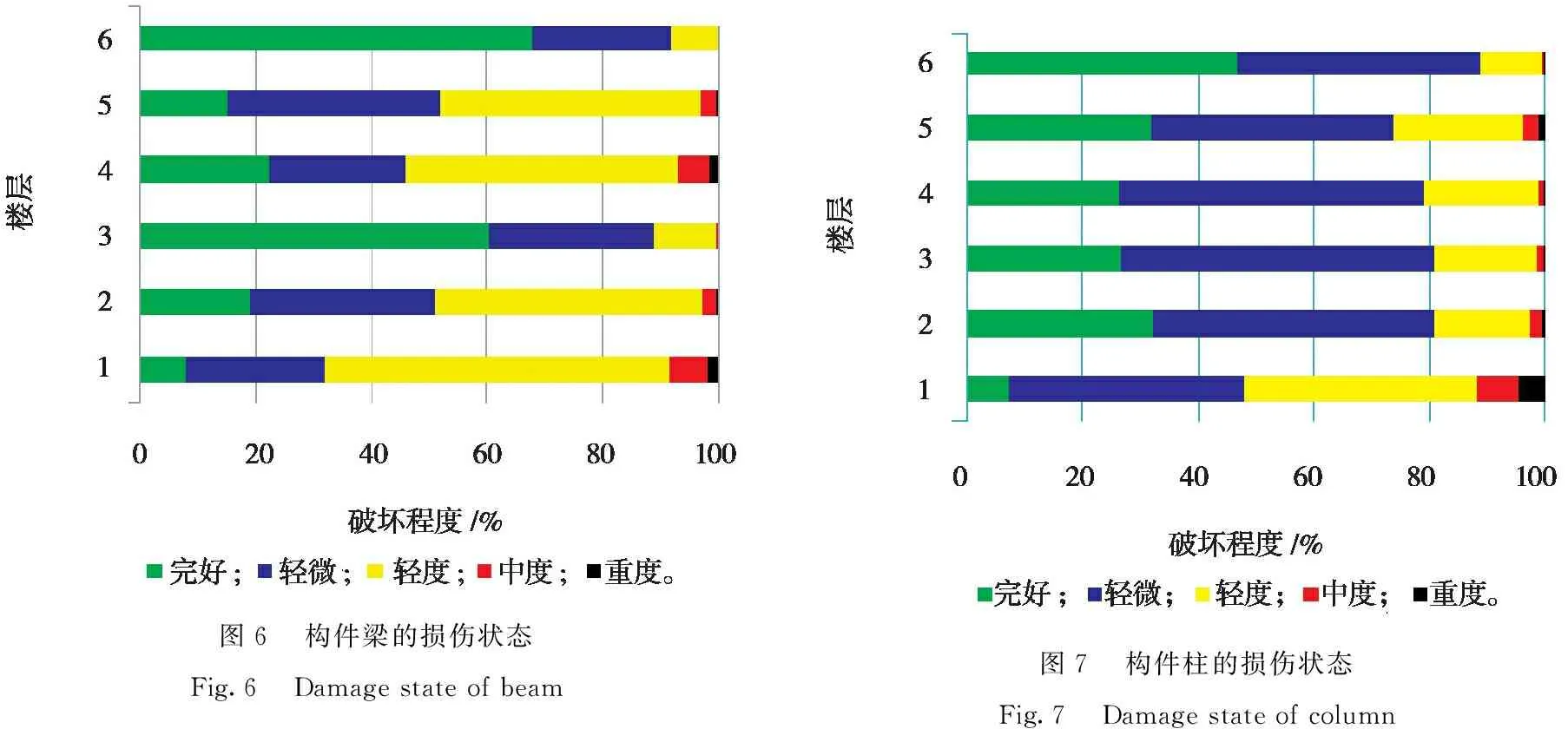
图6构件梁的损伤状态Fig.6Damage state of beam图7构件柱的损伤状态Fig.7Damage state of column

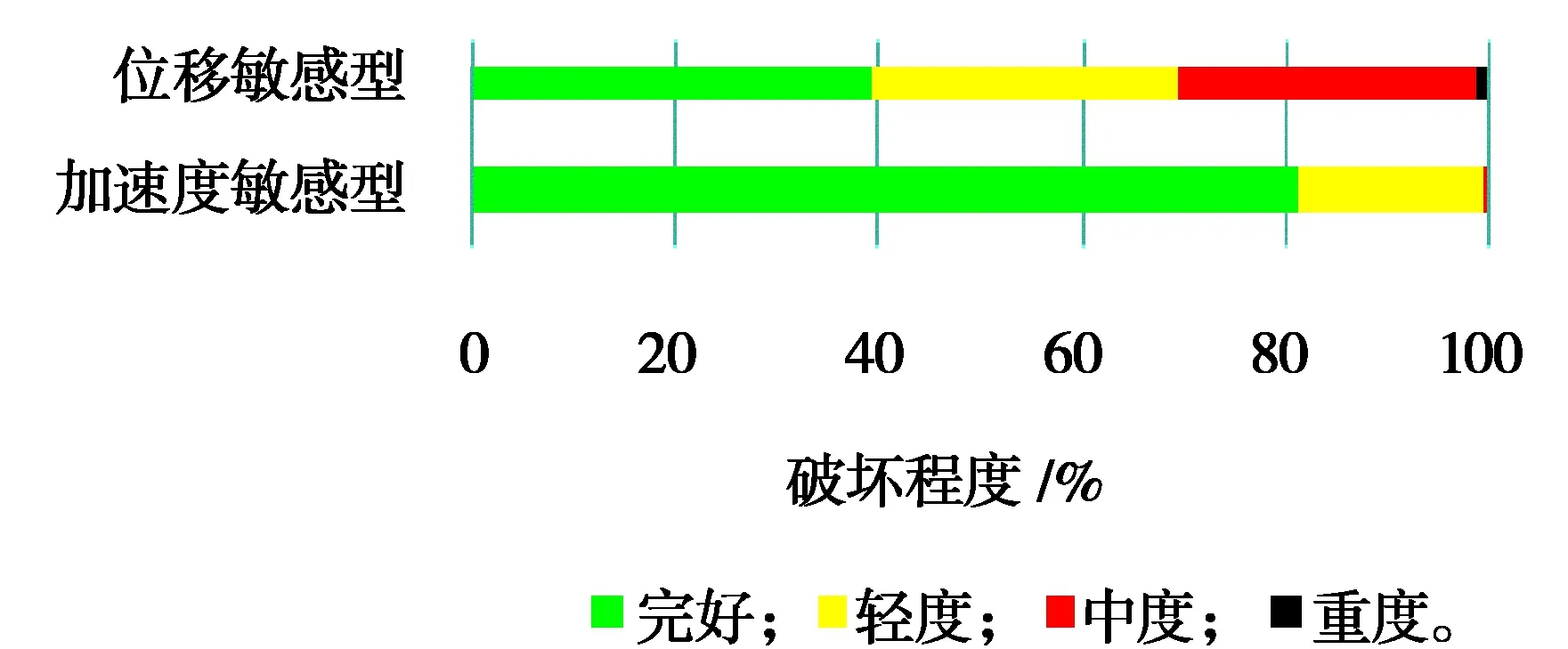
图8 非结构构件的损伤状态Fig.8 Damage state of non-structural components

从梁柱构件以及非结构构件的损伤状态来看，在罕遇地震的作用下，相对于2～6层，底层梁柱构件损伤明显加重。非结构构件中位移敏感型的损伤相较于加速度敏感型更大，说明该框架结构对加速度敏感型非结构构件更加友好。而非结构构件中位移敏感型损伤较大，原因是填充墙、楼梯、隔墙装饰、玻璃幕墙等构件在地震发生时容易发生错位及脱落。

在得到结构各构件以及非结构构件的损伤状态后，由这些损伤状态作为数据支撑进行的韧性评价分析。

3 韧性评价

常规的韧性评价常常考虑人员伤亡、修复时间、修复费用3方面因素[11-14]。而本文则从地震发生后结构的使用功能损伤情况与震后恢复使用功能所需时间两方面来度量该框架结构的韧性。

3.1功能损伤分析结构的使用功能主要由结构构件和非结构构件来提供，功能的损伤情况与结构构件和非结构构件的损伤状态有着直接的关系，依据有关学者已采用的结构使用功能量化方法[15-16]，本文提出了一种衡量使用功能损伤的新计算方法。假定构件的轻微、轻度、中度、重度4种损伤状态对结构造成的影响系数比为1∶2∶3∶4,非结构构件的3种损伤状态轻度、中度、重度对结构造成的影响系数比为2∶3∶4,则结构构件与非结构构件的损伤指数可由相应的损伤状态影响系数值乘以对应的数量再除以总的影响系数与构件总数的积得到。式(1)为结构构件i的损伤指数Si计算方法，其中：Dij为损伤状态为j的i构件，nj为损伤状态为j的构件数量，nt为总构件数量。

(1)

总的功能损伤F的计算公式按式(2)计算。其中：Wki为第k层构件i的重要性系数，Si为结构构件i的损伤指数，Ni为非结构构件i的损伤指数。考虑到非结构构件对结构的使用功能影响最大[15]、以及结构构件的重要性会随高度发生变化，所以假定1～3层结构构件的重要性系数为0.4，非结构构件的重要性系数为0.6。4～6层结构构件的重要性系数为0.3，非结构构件的重要性系数为0.7。损伤指数与功能损失对结构整体的影响值如图8所示。

(2)

图9 损伤指数与功能损失Fig.9 Damage index and function loss

从图9可以看出，结构构件的损伤指数为30.6%，而非结构构件的损伤指数为21.9%。非结构构件的损伤指数值比结构构件的损伤指数值小，其主要原因是非结构构件中加速度敏感型构件较多，且由图7可知加速度敏感性型构件完好率达到了81.4%，从而降低了非结构构件整体的损伤指数值。此外，结构构件的功能损失值为10.7%，而非结构构件的功能损失值为14.2%。非结构构件的功能损失值比结构构件的功能损失值大，由此可知结构的功能损失主要由非结构构件的损坏造成。以上结论均符合常识性规律。

3.2震后恢复时间分析结构修复时间主要由两个阶段构成，一阶段是出于安全性考虑应该先对结构构件进行修复，二阶段是对结构使用功能影响大的非结构构件进行修复。并且应考虑维修过程中存在的并行修复，所以采用已经能成熟应用于工程实例的Redi方法[14]进行修复时间计算，计算结果见图10。非结构构件修复总时间为53 d，占总时间的73%，而结构构件修复总时间为19 d，占总时间的27%。对于整个钢筋混凝土框架结构的修复，非结构构件的恢复时间占据了主导地位。

本研究的钢筋混凝土框架结构是一个单体建筑且无特殊使用功能，所以采取适用于一般情况下的线性函数曲线进行恢复时间的计算。线性函数的公式见式(3)[17]，功能恢复曲线如图11所示。

(3)

其中：Q(t，TR)为使用功能函数，a、b为常数，建议取值[16]：a=-1，b=1。t0为地震发生时刻，TR为恢复时间。由图10可知，框架结构在罕遇地震作用下，建筑功能有明显的损失，结构构件修复时间短，所以一阶段修复过程功能恢复速率快，而非结构构件修复时间长，所以二阶段功能恢复速率慢。由此可知，非结构构件对整个框架结构的韧性起着决定性作用，如果想要结构能快速地从地震造成的破坏中恢复过来，应该着重加强对非结构构件的保护，降低其损伤程度。

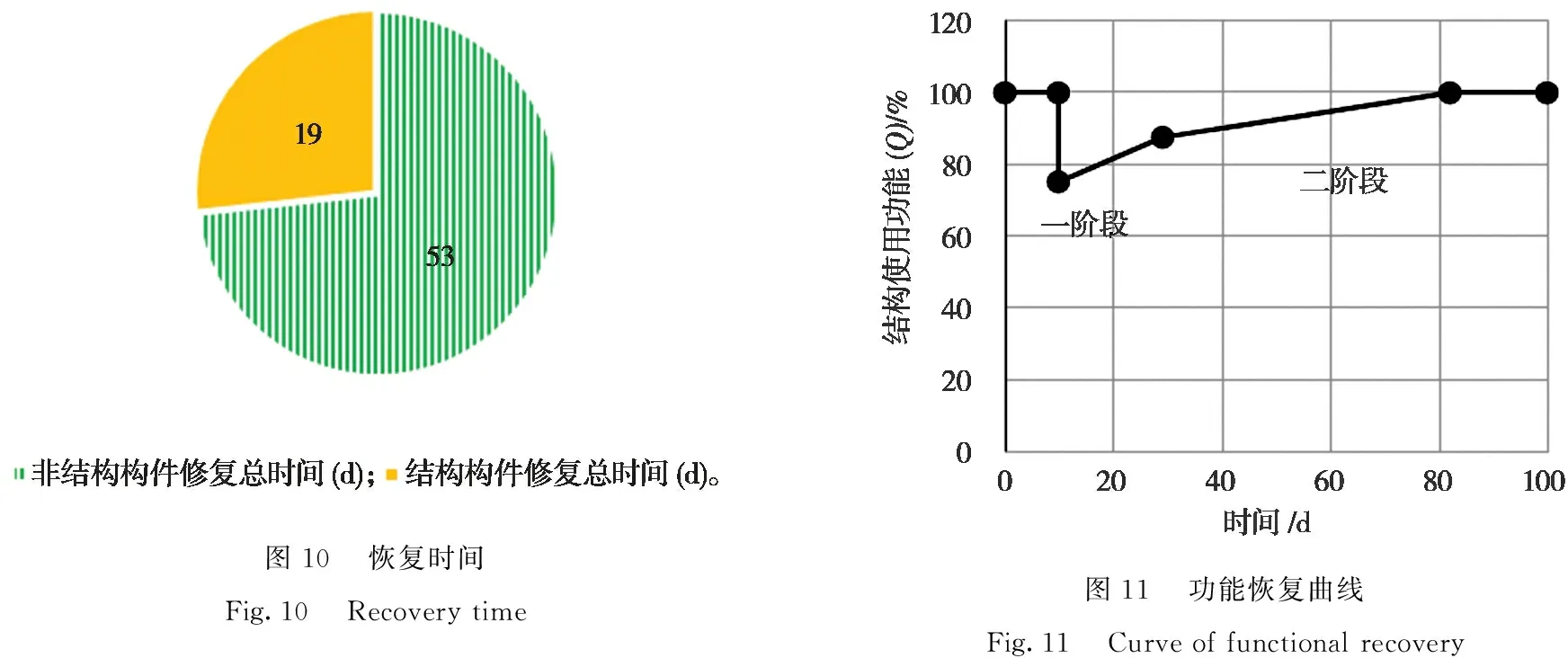
图10恢复时间Fig.10Recovery time图11功能恢复曲线Fig.11Curve of functional recovery

4 讨论与结论

(1)相比于基于医疗系统、能源系统、供水系统等为研究对象的韧性评价[4-6]研究，本文的韧性评价对象是一个具体的6层钢筋混凝土框架结构，通过对该结构进行动力时程分析，并结合编程软件Python，得到了该结构在罕遇地震作用下的梁柱构件与非结构构件的损伤状态，以功能损伤和恢复时间作为评价结构韧性的两个指标，提出了量化功能损失与恢复时间的新方法。通过韧性评价可以看出，非结构构件的破坏程度是个影响整个结构韧性的关键因素，若想大幅度提高结构的韧性能力，应该着重关注对非结构构件的保护。

(2)通过最终的韧性评价结果可知，该钢筋混凝土框架结构在罕遇地震作用下不同楼层的梁柱构件均发生了不同程度的破坏，其中底层的损伤最为明显，完好率最低。在非结构构件中，位移敏感型的轻度损伤、中度损伤、重度损伤都比加速度敏感型的要大，表明非结构构件中位移敏感型损伤程度明显大于加速度敏感型的损伤程度，所以在框架结构中布置位移敏感型构件时应该考虑其易损性。地震对结构构件和非结构构件造成的破坏情况是不同的，结构构件的损伤指数比非结构构件的损伤指数要大，但结构构件所导致功能损失值要比非结构构件要小。由于不同构件对结构使用功能的重要性不一样，所以即使非结构构件的损伤情况没有结构构件严重，也要注意到结构的使用功能主要是由非结构构件提供。结构构件修复时间短，结构功能能快速恢复，非结构构件修复时间长，结构功能恢复缓慢。所以对非结构构件进行保护，降低其在地震灾害发生时的损伤程度能在很大程度上提高结构的韧性。