基于灰色多元线性回归的上海某办公建筑空调能耗预测模型

豆晨昊 徐 峰

基于灰色多元线性回归的上海某办公建筑空调能耗预测模型

豆晨昊 徐 峰

（上海交通大学船舶海洋与建筑工程学院 上海 200240）

能耗预测可以为建筑管理人员提供空调系统未来运营期间的能耗额以及增长趋势，以便制定相应的节能策略。主要讨论空调能耗的影响因素及各因素的影响程度，将灰色模型和多元线性回归模型结合，基于灰色多元线性回归建立空调能耗预测模型。首先，以上海某办公建筑为例，通过灰色模型对空调能耗的异常能耗值及室外天气温度、湿度的观测值进行修正，降低数据的随机波动性，得到灰色模型修正数据；然后，计算影响因素与空调能耗额之间的相关性系数，讨论各因素对空调能耗的影响程度；最后，利用灰色模型修正数据建立灰色多元线性回归空调能耗预测模型，并将空调能耗预测值和实际值相对比，结果表明，构建的灰色多元线性回归预测模型符合多元线性回归建模要求，并具有较高的能耗预测精度。

灰色理论；办公建筑；灰色多元线性回归模型；空调能耗

0 引言

2018年上海市住房和城乡建设管理委员会发布的《2018年度上海市国家机关办公建筑和大型公共建筑能耗监测及报告分析》[1]（以下简称《报告》）的数据显示，办公建筑年单位面积耗电量年耗电量为97.4kWh/m2，其中供热季能耗约为32kWh/m2，过渡季能耗约为27.4kWh/m2，制冷季能耗约为38kWh/m2。从整体能耗角度来看（见图1），办公建筑能耗占所有建筑类型能耗的28.1%，属于上海市公共建筑能耗最高的建筑类型。

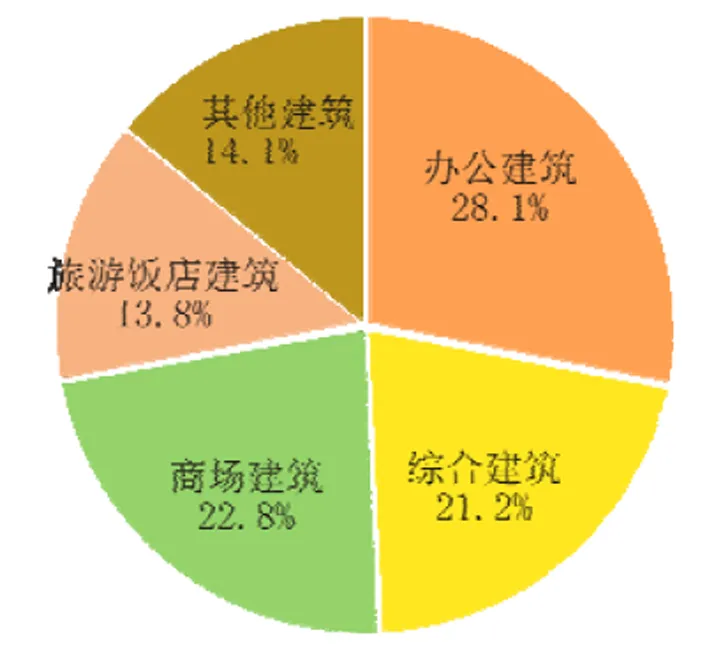
图1 2018年上海市不同类型建筑年耗能占比

办公建筑用电能耗结构（见图2）中空调系统能耗占比29.8%，是办公建筑运营期间能耗大项，“十三五”国家发展规划纲要中提出单位GDP能耗下降20%的节能目标，其中建筑节能承担着巨大的节能减排任务，构建空调能耗预测模型预测未来空调系统的能耗，采取相应的措施降低空调系统能耗是很有必要的。

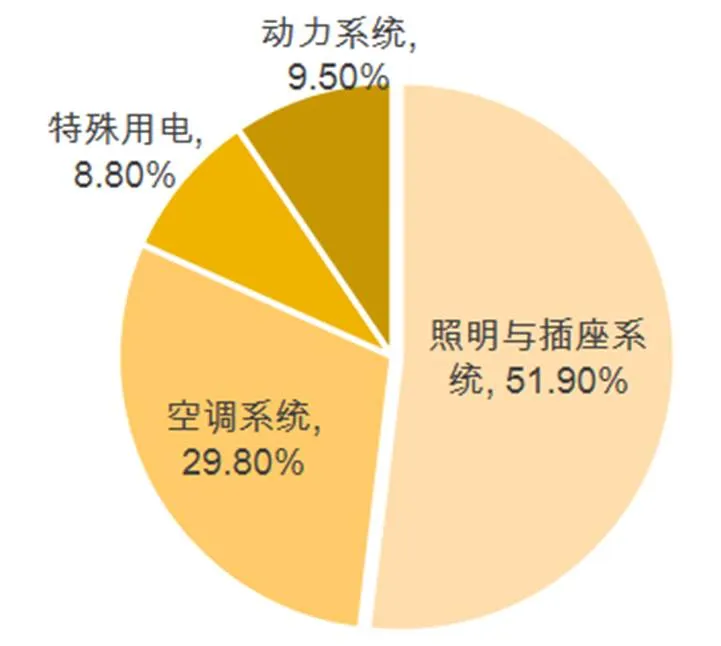
图2 2018年上海市办公建筑不同用电系统年耗能占比

江亿[2]等人研究了不同情况下空调系统的节能潜力，表明空调系统在使用得当的条件下可以进一步降低能耗。空调能耗预测模型可以预测建筑未来能耗增长趋势，研究空调系统运行能耗的特点以及影响因素，为管理者开展建筑节能工作提供参考。

目前许多学者采用了不同的预测方法预测建筑能耗，在智能算法方面，王定奥[3]等人利用DeST软件模拟建筑内多因素影响下的空调运行状态得出仿真数据，然后构建多变量参数预测数据的BP神经网络对仿真数据进行拟合，得出空调能耗预测模型。陈彦熹[4]等人基于人工神经网络建立办公建筑的空调风系统和地源热泵空调预测模型，该模型精度高，而且需要输入的初始参数较少，仅需建筑运行数据和气象参数即可得出能耗预测值。廖文强[5]等人考虑到数据的时序性和非线性关系，利用可以很好地适应这种特点的长短期记忆神经网络，构建暖通空调系统能耗预测模型。由于利用传统的能耗分析软件建立的能耗预测模型不能很好地适用时刻改变的环境参数，Xu Yang[6]等人考虑建筑内部环境参数，利用ELM（extreme learning machine）算法构建了空调能耗预测模型。

在利用历史数据建模的方法上，周芮锦，潘毅群[7]等人利用时间序列法预测和分析商业建筑能耗，构建全年建筑总能耗的预测模型。马忠娇[8]等人通过分析历史数据，假定天气情况，工作日与非工作日条件相同的条件下，建立基于室外空气温度和照明插座用电量相似的组合权重的精确空调能耗预测模型。验证表明，该模型实际误差在5%以内。杨柳[9]等人首先利用Energy Plus分析办公建筑的能耗影响性因素，然后利用多元线性回归法建立建筑能耗预测模型。

以上提到的能耗预测模型建模方法主要有时间序列法、人工神经网络法、相似工况预测法以及多元线性回归法。时间序列法是考虑到时间顺序排列的数据预测未来的方法，但是这种方法局限性在于只适合中短期预测，当外界因素发生变化时，预测结果有时不符合实际规律[10]。人工神经网络法是一种是模拟人脑神经元的智能算法，可以适应复杂多变的情况，具有自我学习的功能，但局限性在于需要大量的数据，并且无法研究模型中每一个参数的特点，不能具体讨论每一个影响因素对因变量的影响程度大小。相似工况预测在历史日和预测日相似的的前提下具有较高的精度，构建的模型依赖于历史数据，如果未来的预测日和历史日相似度比较低，则会产生较大的偏差[8]。

多元线性回归的方法可以充分考虑各个影响因素的特点，分析影响因素对空调能耗的影响程度。利用灰色多元线性回归模型对数据要求不高，无需大量的时间进行模型训练，省时省力，并且不过分依赖于历史数据。本文先以灰色理论修正数据，再分析各个影响因素与空调能耗之间的相关性，以及各个因素对空调能耗的影响程度，并将灰色理论和多元线性回归模型结合，以灰色模型修正过的数据构建基于灰色多元线性回归的空调能耗预测模型。

1 模型建立

原始观测数据若存在较大的随机波动性，建立预测模型时不利于发现规律，且建立的模型预测准确性也不高，考虑到这个问题，先利用GM(1,1)修正观测数据。

1.1 GM(1,1)模型

灰色模型多用于预测以及修正波动性较大的观测数据。在建模时，若原始数据受到外界扰动因素影响波动性较大，呈现的规律性不明显，则会降低模型的预测精度。适当修正原始数据可降低数据的随机波动性、减少误差，进而更能反映数据本身的规律以及预测的趋势，提高数据的预测精度。GM(1,1)模型在其他领域也得到广泛的应用，李俊峰[11]利用GM(1,1)模型估计上海市的发电量；宋晓华[12]利用GM（1,1）模型修正原始序列，将GM(1,1)模型和支持向量机（SVM）相结合，建立长期电量预测模型，将预测相对误差控制在2.06%。

本文将GM(1,1)模型与多元线性回归模型相结合，用matlab实现GM(1,1)模型，再利用GM(1,1)模型修正原始序列，降低原始序列的波动性，然后以修正的原始数据建立办公建筑空调系统灰色多元线性回归能耗预测模型。

若设原始数据序列为：

一次累加方法为：

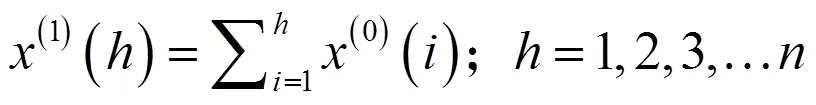
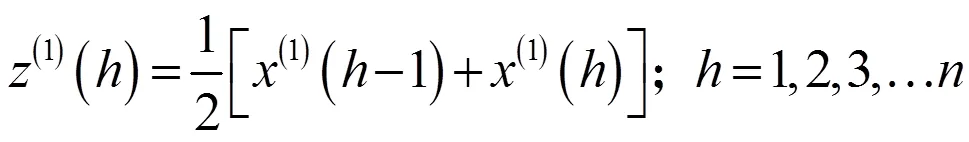
GM(1,1)所对应的一阶一元微分方程：

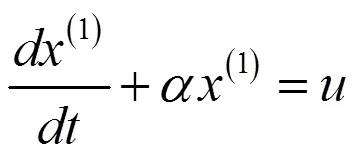
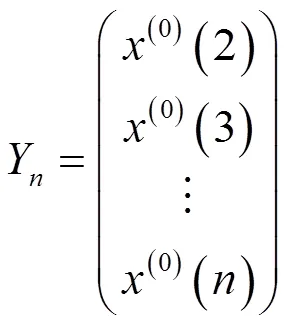
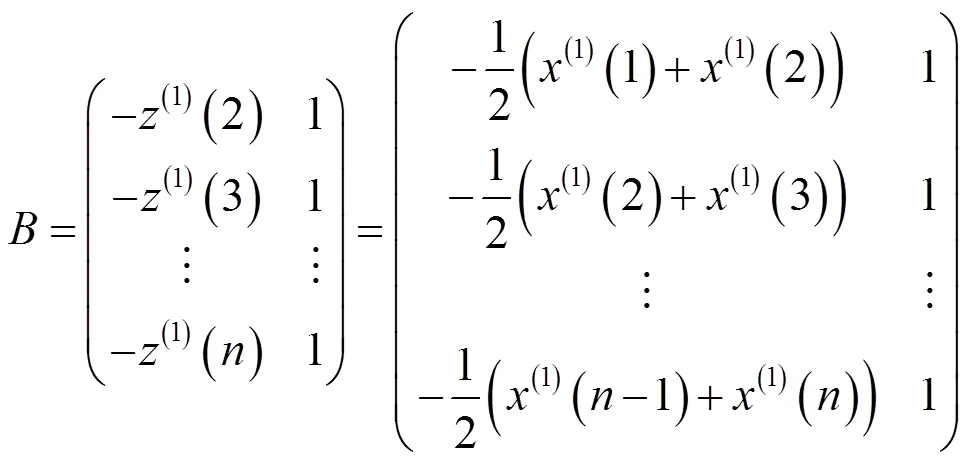
将灰参数代入

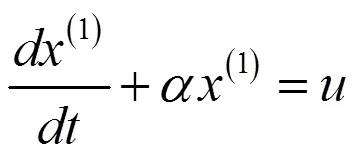
得：

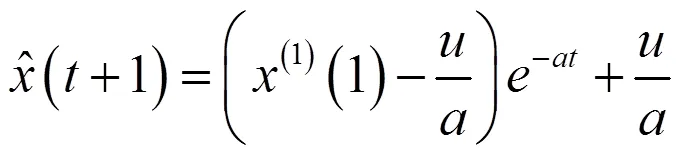
将上述结果累减还原：

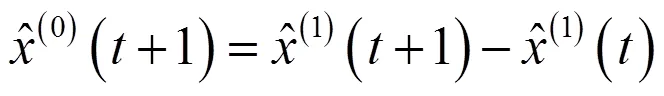
得到原始数据的修正值为：

1.2 相关性分析

相关性分析主要目的是研究变量间关系的密切程度[13]，在统计分析中，常利用相关系数定量地描述两个变量线性关系的紧密程度，相关系数取值区间为[-1,1]。线性相关系数绝对值越大则表明两变量之间的相关性越强。本文采用相关分析，来研究温度和湿度与空调能耗额之间的相关性。

相关系数：

线性相关是用来度量具有线性关系的两个变量之间相关密切程度以及相关方向，线性相关系数又称相关系数，也称积差相关系数。

（1）值（也称显著性值或sig值），判断两个变量之间是否存在显著相关关系。

如果<0.05，则表明两者之间具有相关性。<0.01使用2个*号表示；<0.05使用1个*号表示。

（2）相关系数：判断两者之间相关性的强弱。

相关系数绝对值相关性强弱 0.8-1.0极强相关 0.6-0.8强相关 0.4-0.6中等程度相关 0.2-0.4弱相关 0.0-0.2极弱相关或无相关

相关系数为：

（7）

其中，为样本容量，x和y为所检验相关性的两变量对应的样本值

检验统计公式为：

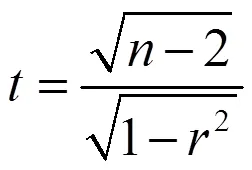
即：统计量服从自由度为-2的分布。

1.3 多元线性回归模型

1.3.1 多元线性回归模型建模的步骤

在线性回归分析中，影响因变量变化的因素包含两个或两个以上的自变量，且因变量与自变量之间存在线性关系，则称为多元线性回归分析。

此时：

，

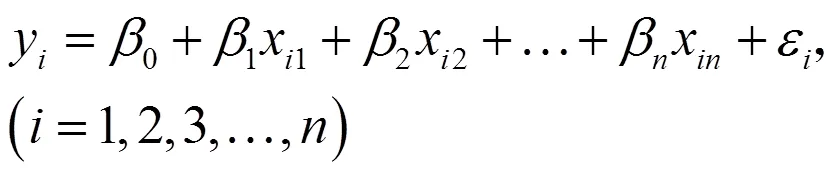
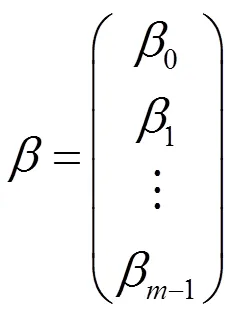
以矩阵形式表示即为：

（10）

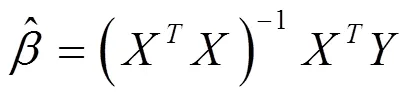
1.3.2 多元线性回归模型的检验

利用SPSS22.0建立多元线性回归分析模型，得出模型后需要检验分析模型是否符合建模要求，检验方法主要分为相关系数检验、检验和检验。

具体而言：

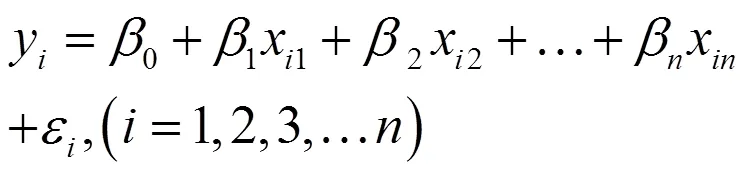
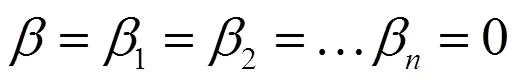
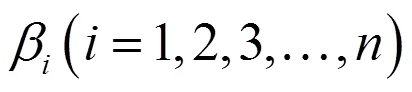
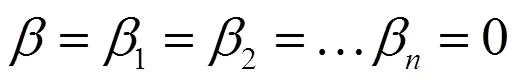
（1）相关系数的检验

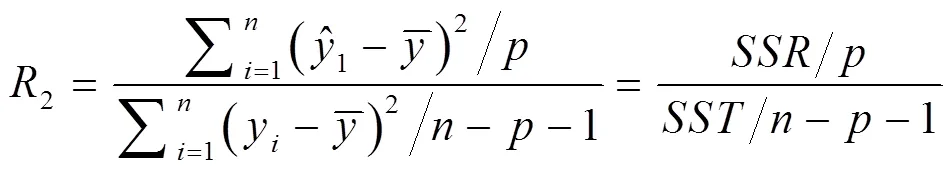
其中，和（--1）为自由度，=+

判断条件：2值越接近于1，说明，之间的相关性越强。若2为0，则说明与之间无关。

（2）检验

（14）

判断条件：

（3）检验

（15）

其中，

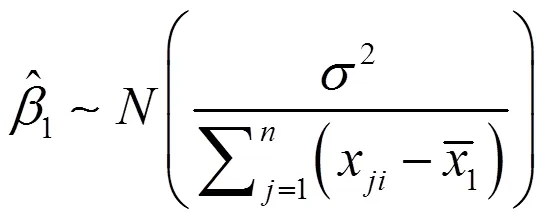
判断条件：

2 案例应用

本文以上海某办公建筑为例建立灰色多元线性回归模型，验证灰色理论与多元线性回归模型结合的可行性。由于每年过渡期间空调使用较少，而供冷季空调使用量更加集中，分析供冷季空调能耗与天气温度、湿度之间的关系更能体现出空调系统运行的特点。节假日、休息日以及下班期间空调系统处于关闭状态，此期间的能耗数据不具有研究代表性，故本文案例采用2018年的6、7、8月的上海某办公建筑的除去节假日、周末休息日的正常工作期间每天该建筑上班时间的7点-17点的空调系统能耗额，以及上海2018年室外天气温度和湿度的历史数据。表1为截取分析数据观测值的某一天的数据。

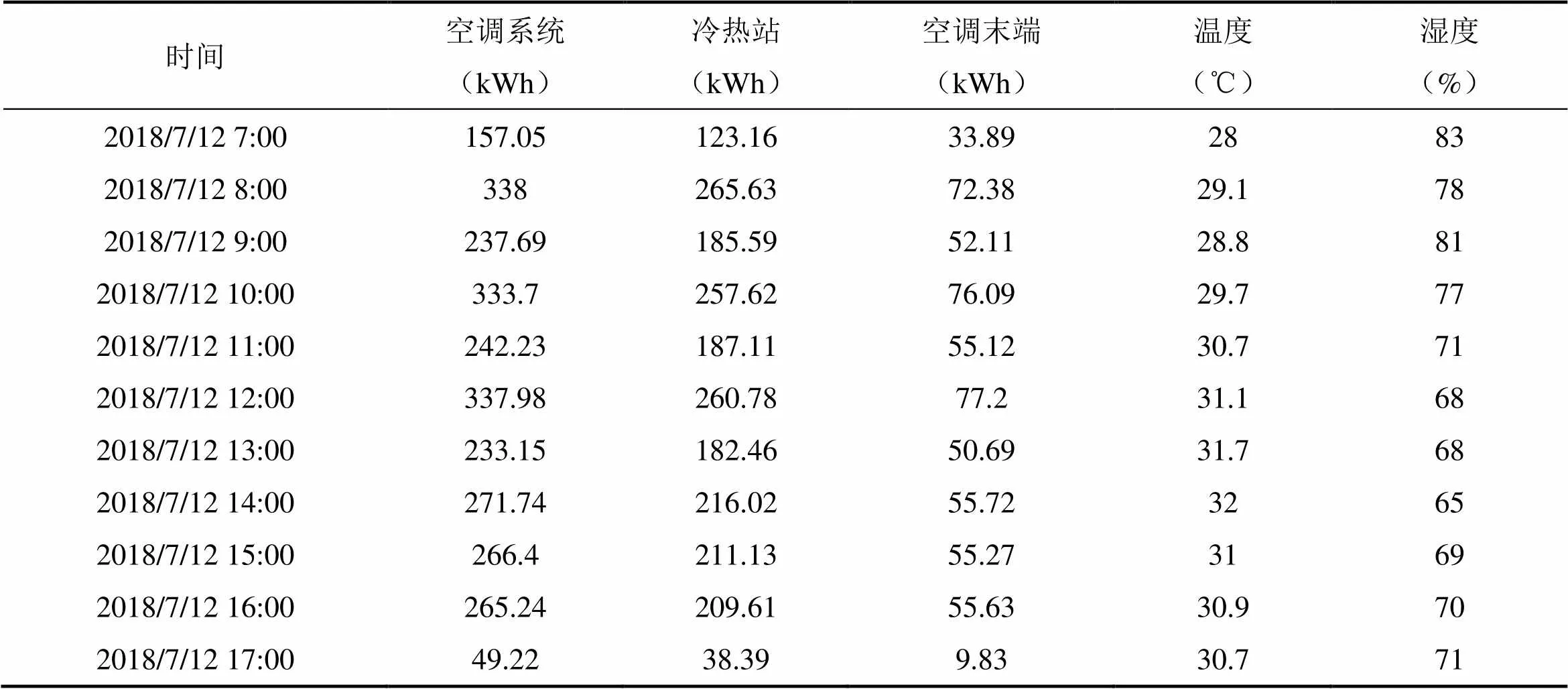
表1 截取分析数据某一天的分析数据

注：（1）该建筑的上班时间为8:30-17:00；（2）8-9时的空调能耗比7时显著增高，这是由于员工上班后空调启动时的能耗比正常运行时能耗大。

2.1 修正观测数据

由于空调开启时的能耗异常值以及建筑内人员的行为因素导致了数据的波动性变大，为了增加模型的预测精度，首先利用GM(1,1)对原始数据序列进行数据修正处理，得到原始数据的修正值，此处截取某一天的空调能耗数据为例，如表2所示。

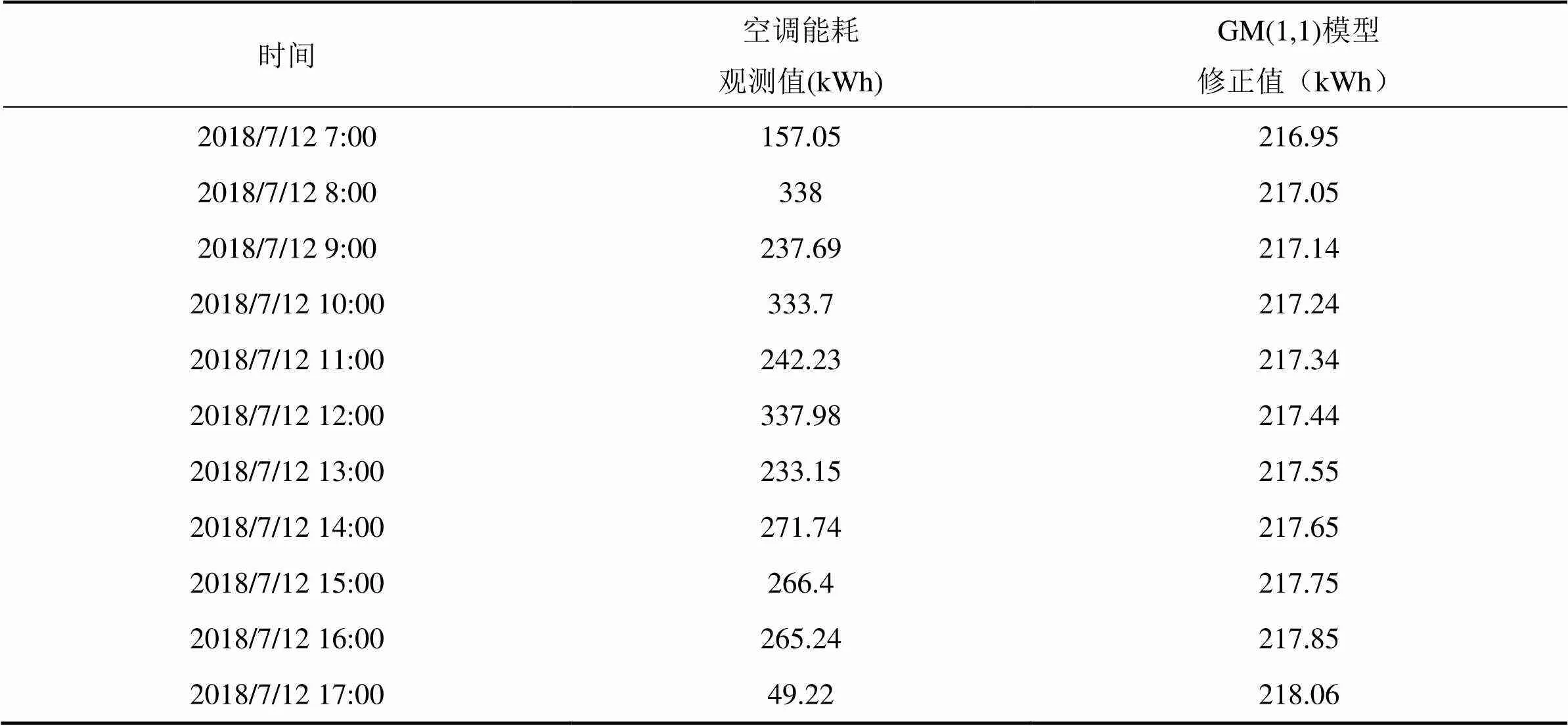
表2 GM(1,1)模型修正某一天空调能耗值

此时输入空调能耗的观测值：

输出的空调能耗修正值为：

观察这一天的数据，空调能耗在8时、10时、12时和17时中有突变值，主要是因为8:30、9:30员工上班相继开启空调，造成这些时段空调能耗突然增高。11:20是员工的午餐时间，办公楼内办公区域的空调仍然开启，但是办公楼餐厅人流量增加，局部过密的人流导致空调能耗也相应会增加。在17:00左右员工陆续下班关闭空调，所以空调能耗骤降。由于这些外界影响因素导致了空调能耗值产生了异常值，增加了数据的波动性，若这些异常的空调能耗值参与空调能耗预测模型建模，对于其他正常时间段空调能耗的预测是有影响的，但经GM(1,1)模型优化异常的空调能耗值，削减了过高的异常值，可以提高空调能耗预测模型的精度。

2.2 相关性分析

2.2.1 散点图分析

利用SPSS22.0绘制散点图，通过散点图可以直观地看出变量之间的相关性程度。散点图结果如图3、4所示。

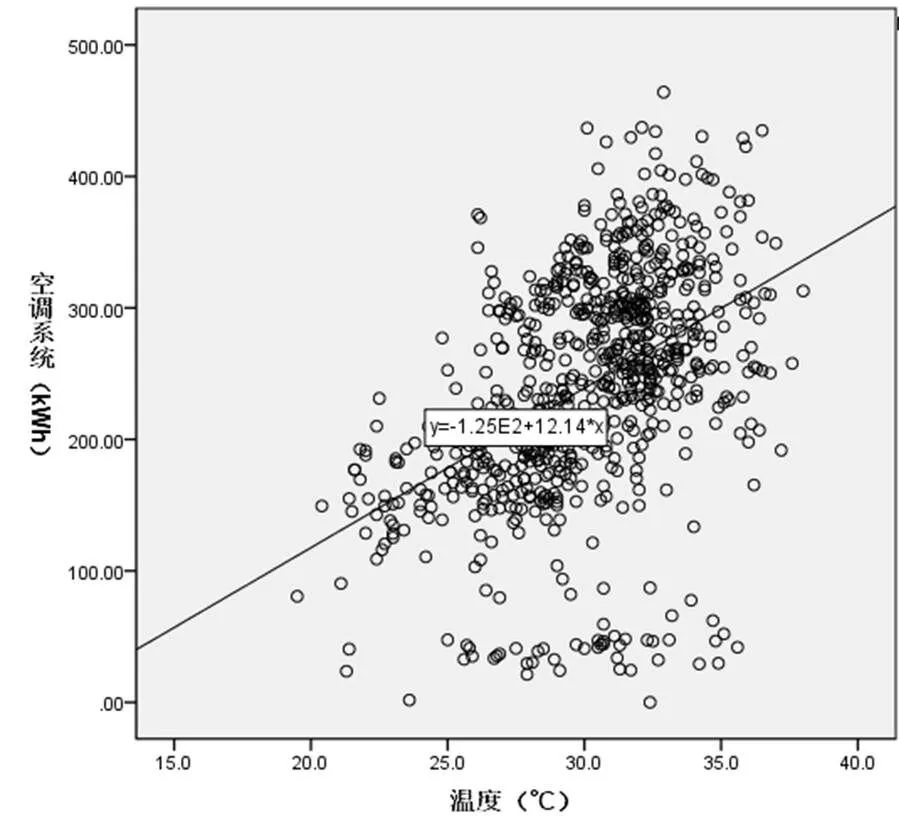
图3 温度与空调系统能耗之间的散点图

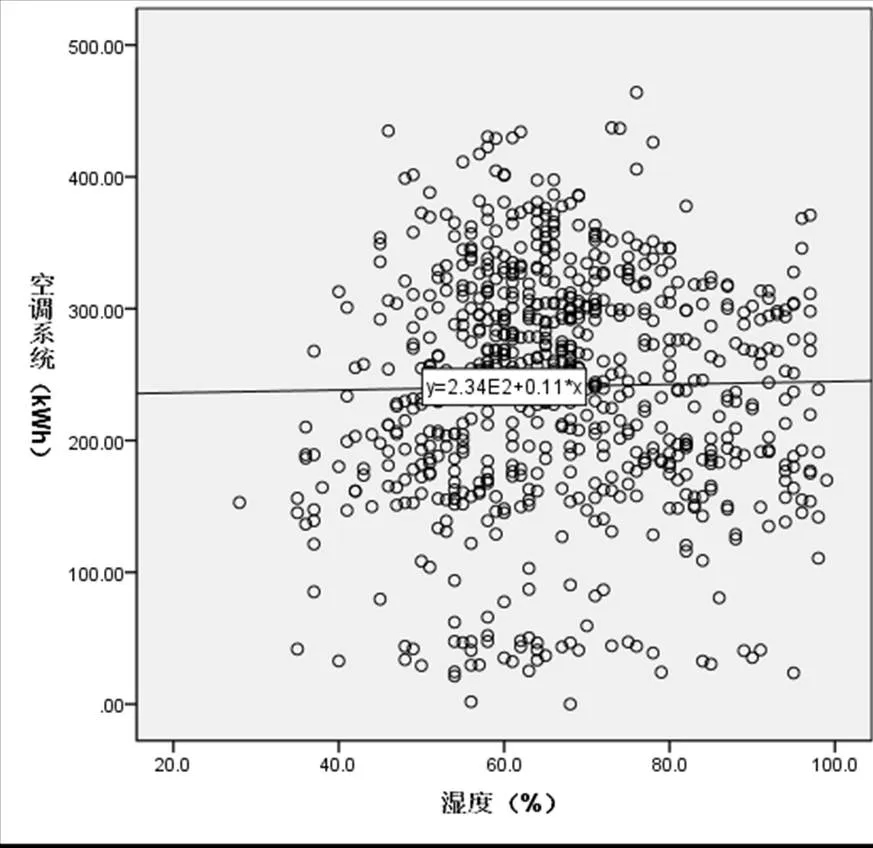
图4 湿度与空调系统能耗之间的散点图

从空调系统能耗与室外温度、湿度的散点分布图可以看出制冷季期间的温度明显与空调系统能耗呈现正相关性，但是湿度与空调系统能耗之间的相关性并不明显。

2.2.2 统计学分析

本文采用相关性分析，为了对比灰色模型修正前、后数据的特点，本文用SPSS22.0软件对温度与空调能耗、湿度与空调能耗进行相关性分析，修正前后的结果对比如表3所示。

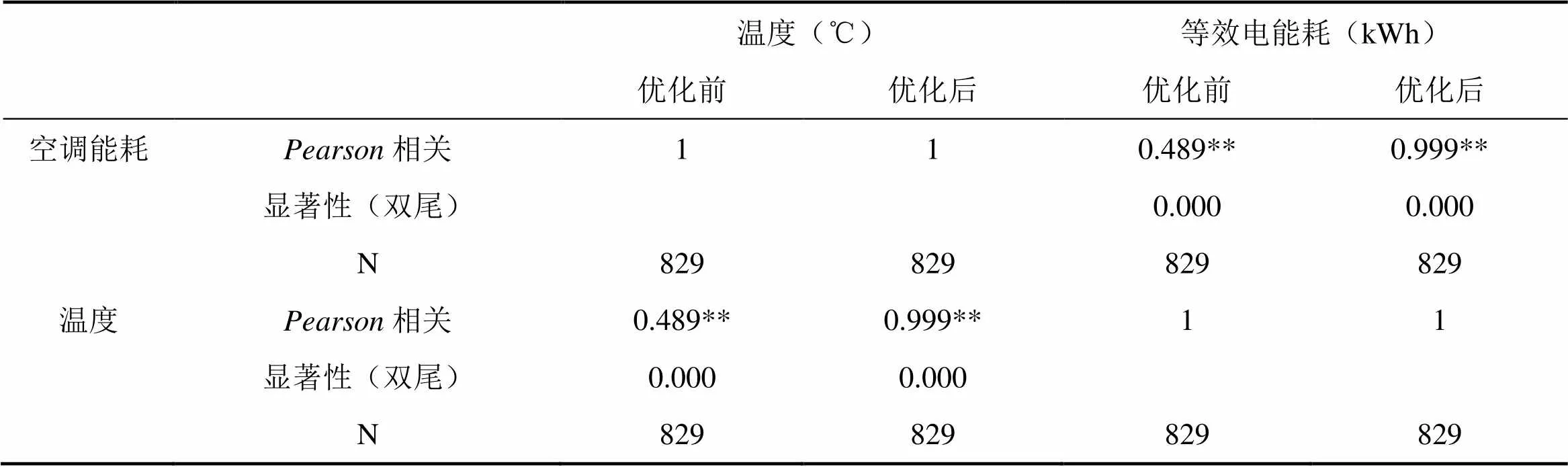
表3 修正数据前后温度与空调能耗之间的相关性分析结果对比

注：**相关性在0.01层上显著（双尾）。

结果分析：数据修正后，相关系数由原来的0.489上升到0.999，修正后的数据明显比修正前的数据与空调能耗有更明显的相关性，呈极强相关。这是由于GM(1,1)修正后的数据削减了异常能耗值，降低了数据的随机波动性，进而增强空调能耗与温度之间的相关性。

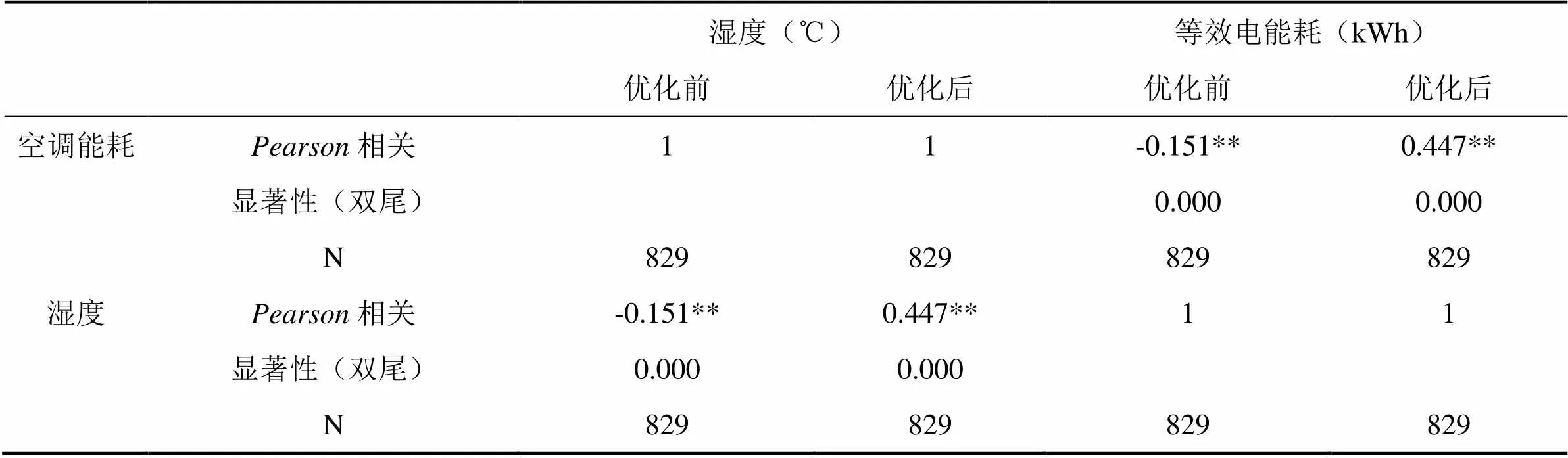
表4 修正数据前后湿度与空调能耗之间的相关性分析结果对比

注：**相关性在0.01层上显著（双尾）

结果分析：原始数据中每天中午时湿度最低的时候，但是此时空调能耗却比较高，所以导致了呈现非常弱的负相关的错误相关性归分析结果。优化后的数据分析结果呈现的是中等相关，符合空调系统运行能耗的特点。从相关系数来看，数据修正后的湿度与空调能耗之间有更明显的相关性，呈中等程度相关。

温度与空调能耗之间的相关系数要大于湿度与空调能耗之间的相关系数，表明温度与空调能耗之间的相关性更紧密，温度对空调能耗的影响程度要大于湿度。

2.3 建立灰色多元线性回归模型

经GM（1.1）修正后的数据结合多元线性回归模型，建立灰色多元线性回归空调能耗预测模型，并对灰色线性回归模型的拟合程度进行检验，相关系数检验、检验和检验结果分别如下表所示。

表5 R2检验

注：预测值：（常数）温度、湿度。

表6 F检验

注：应变数：空调能耗；预测值：（常数）温度、湿度。

表7 t检验

注：应变数：空调能耗。

以上结果显示灰色多元线性回归方程拟合结果良好，得到灰色多元线性回归方程为：

（17）

式中，为空调能耗预测值；为温度；为湿度。

本文以上海某办公建筑6、7、8月空调能耗观测值建立多元线性回归空调能耗预测模型，求出与9月份实际观察值之间的差值以及差值百分比，从而验证灰色理论与多元线性回归模型结合方法的合理性以及模型预测精度。下表是截取的某一时间段的对比值。

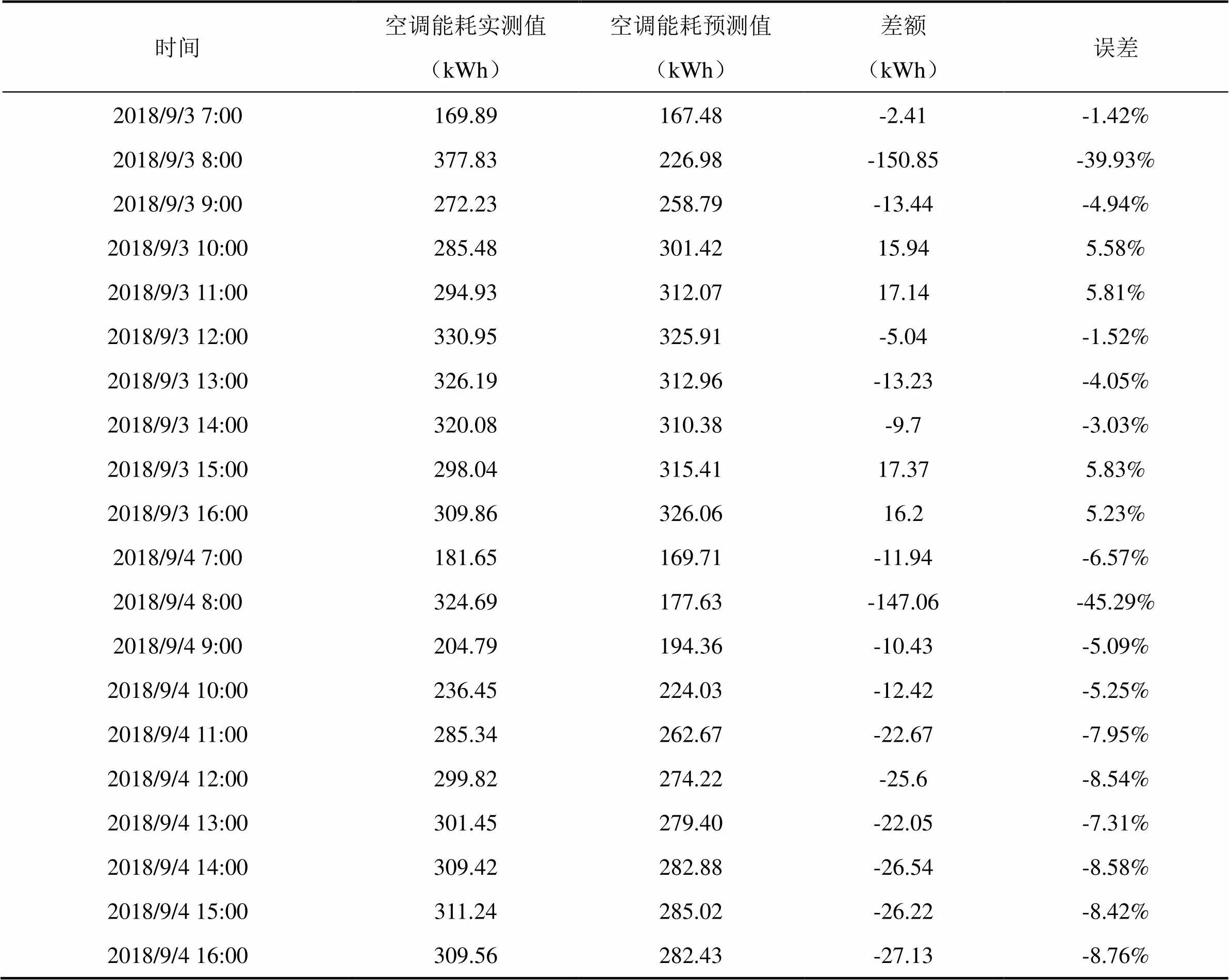
表8 模型检验

需要注意的是，根据办公楼运营时间，每天早上8点-9点是员工上班时间，此时会陆续开启空调，开启空调时电量消耗比普通运行模式情况下大，所以造成了预测能耗与实际能耗之间的差值较大。结果显示，除去空调开启时间段能耗差异值较大，其余时间预测结果显示有较高的精度。将GM（1,1）模型修正后的数据与多元线性回归法相结合，建立的灰色多元线性回归模型拟合精度较高，符合建模要求。

3 结论

本文是根据逐时的温度和湿度数据建立灰色多元线性回归模型，在实际使用空调过程中，由于空调系统不正当使用等因素导致了空调系统能耗的浪费，管理者可以根据天气气象参数得出空调能耗预测值，然后根据预测值设定本建筑空调系统的能耗阈值，建立节能规章制度，减少不必要的能耗浪费。

（1）根据相关性分析结果，温度与空调能耗之间的相关性系数明显高于湿度与空调能耗之间的相关性系数，说明温度对空调系统能耗的影响程度要高于湿度。

（2）经过灰色理论修正过的温度、湿度与空调能耗之间的相关性明显增强，灰色理论降低数据的随机波动性的效果是显著的。并且根据灰色模型优化前后的数值拟合方程效果对比，灰色模型优化后的数据在建立多元线性回归模型时拟合精度要高于原始数据的，说明降低外界因素对于数据造成的波动可以提高模型的预测精度。

（3）灰色多元线性回归空调能耗预测模型有较高的预测精度，即灰色理论与多元线性回归模型相结合的方法是可行的。

[1] 2018年上海市国家机关办公建筑和大型公共建筑能耗监测及分析报告[R].上海:上海市住房和城乡建设管理委员会,2018.

[2] 江亿,薛志峰.北京市建筑用能现状与节能途径分析[J].暖通空调,2004,(10):17-20.

[3] 王定奥,刘清惓,戴伟,等.基于BP神经网络的空调能耗预测与监控系统[J].现代电子技术,2019,42(22):140- 144.

[4] 陈彦熹,刘建华,李旭东,等.基于ANN的绿色办公建筑HVAC系统运行能耗预测[J].建筑节能,2017,45(10): 1-5.

[5] 廖文强,王江宇,陈焕新,等.基于长短期记忆神经网络的暖通空调系统能耗预测[J].制冷技术,2019,39(1):45- 50,54.

[6] X Yang, et al. A forecasting method of air conditioning energy consumption based on extreme learning machine algorithm[C]. 2017 6th Data Driven Control and Learning Systems (DDCLS), Chongqing, 2017:89-93.

[7] 周芮锦,潘毅群,黄治钟.基于时间序列分析的建筑能耗预测方法[J].暖通空调,2013,43(8):71-77.

[8] 马忠娇,张吉礼.基于相似工况组合权重的空调能耗预测方法[J].建筑热能通风空调,2017,36(12):13-18.

[9] 杨柳,侯立强,李红莲,等.空调办公建筑能耗预测回归模型[J].西安建筑科技大学学报(自然科学版),2015,47 (5):707-711.

[10] 沙国荣,钱青.人工智能算法在建筑能耗预测中应用综述[J].科技创新与生产力,2018,(9):58-59,62.

[11] 李俊峰,戴文战.GM(1,1)改进模型的研究及在上海市发电量建模中的应用[J].系统工程理论与实践,2005, 25(3):140-144.

[12] 宋晓华,祖丕娥,伊静,等.基于改进GM(1,1)和SVM的长期电量修正组合预测模型[J].中南大学学报(自然科学版),2012,(5):1803-1807.

[13] 李昕,张明明.SPSS 22.0统计分析[M].北京:电子工业出版社,2015.

Air Conditioning Systems Energy Consumption Prediction Model of Office Buildings Based on Grey-multiple Linear Regression Theory

Dou Chenhao Xu Feng

( School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiaotong University, Shanghai, 200240 )

Energy consumption prediction model can provide building managers with energy consumption value and growth trend during the futural operation, so as to facilitate managers to make relevant energy-saving strategies. This paper mainly discusses the influence degree of influencing factors on air conditioning system and establishes the air conditioning energy consumption prediction model based on the combination of grey model and multiple linear regression model. Firstly, the grey model is used to modify the air conditioning energy consumption value of an office building in Shanghai and the observation value of outdoor weather temperature and humidity in 2018, which can reduce the random volatility of collected data. Secondly, calculating correlation coefficient between the influencing factors and air conditioning energy consumption, in order to explore the influence degree of the energy influencing factors. Finally, the grey multiple linear regression energy consumption prediction model is established by using the emendated data. This paper analyzes the influence degree of influencing factors on air conditioning energy consumption, and established grey multiple linear regression prediction model meets the requirements of multiple linear regression modelling and obtains high accuracy of energy consumption prediction.

Grey theory; office buildings; grey-multiple linear regression model; air conditioning systems energy consumption

1671-6612（2021）03-352-08

TU831

B

国家科技部国家重点研发计划子课题“基于BIM的绿色建筑运营成本控制技术（编号：2018YFC0705901-04）”

豆晨昊（1995-），男，在读硕士研究生，E-mail：douchenhao1995@163.com

徐 峰（1970-），男，硕士生导师，副教授，E-mail：F.Xu@sjtu.edu.cn

2020-08-17