全工况下离心式制冷压缩机轴向力数值分析

衣可心 赵远扬 王 春

全工况下离心式制冷压缩机轴向力数值分析

衣可心 赵远扬 王 春

（青岛科技大学机电工程学院 青岛 266061）

离心压缩机广泛应用于商用空调系统中，气悬浮技术是离心式制冷压缩机重要发展方向之一，但需承载压缩机轴向力的气体轴承的承载能力较小。因此，以离心式制冷压缩机闭式叶轮为研究对象，采用数值方法对叶轮在全工况下的轴向力进行了模拟分析。研究结果表明：当压缩机运行于稳定工况范围时，叶轮轴向力随压比的增大而减小，随流量的减小而减小，但当压缩机工作点接近喘振区和阻塞区时，轴向力明显增大；叶轮轴向力随转速的增大而减小，密封直径对叶轮所受轴向力影响较大；设计工况下的轴向力数值计算与理论计算的误差为4.4%。

离心压缩机；叶轮；轴向力；气悬浮；CFD数值方法

0 引言

离心压缩机广泛应用于商用空调系统中，叶轮是离心压缩机最重要的部件[1,2]。在离心制冷压缩机运行时，旋转叶轮流道内的气流由于流速和压力会对叶轮产生冲击，加之叶轮外侧的轮盖与轮盘所受压力的作用，以及密封间隙区域的气流影响，使得叶轮会产生一个沿轴向的力[3,4]。由于叶轮的轮盘和轮盖两侧所受的气体作用力不同，相互抵消后，还会剩余部分轴向力作用于转子，这部分轴向力由止推轴承来承担。如果轴向力过大，会影响轴承寿命，严重时会使机器损坏，甚至影响整个机组的安全[5-7]。

传统离心制冷压缩机采用齿轮增速方式提高其叶轮转速，使用油膜滑动轴承承受其轴向力，该轴承承载力较大[8]。近年来，磁悬浮制冷离心压缩机逐渐成熟并应用，该压缩机采用高速电机直接驱动，使用磁悬浮轴承，该轴承的承载力比油膜滑动轴承的承载力低[9,10]。采用气体轴承替代磁悬浮轴承的气悬浮制冷离心压缩机是制冷离心压缩机的发展方向之一[11]。气悬浮制冷离心压缩机不仅克服了传统齿轮增速结构的缺点，而且还具有成本低、无需主动控制等优点，但相比于油膜滑动轴承和磁悬浮轴承，气体轴承的承载力较低[12]。所以，准确并详细的分析全工况下的轴向力，是气悬浮离心制冷压缩机结构设计的关键问题。

以往离心压缩机轴向力的计算均是利用传统的理论计算方法，只能得到设计工况下的轴向力[13]。而制冷压缩机的运行工况是复杂多变的，需要根据环境温度和负荷不断调整其运行工况，这会带来其轴向力的变化。因此，本文以离心制冷压缩机为研究对象，采用CFD数值方法对叶轮在全工况下的轴向力进行模拟分析，研究压比、流量、转速、密封直径等参数对轴向力的影响。

1 轴向力理论计算

离心压缩机叶轮轴向力分为轮盖侧轴向力和轮盘侧轴向力。如图1所示，从入口直径D到出口直径2范围内叶轮两侧的气体压力大小相等、方向相反，不会产生轴向力。因此，叶轮的轴向力就是轮盖侧从轮毂直径d到D和轮盘侧从密封直径d到D间气体作用的结果[14,15]。

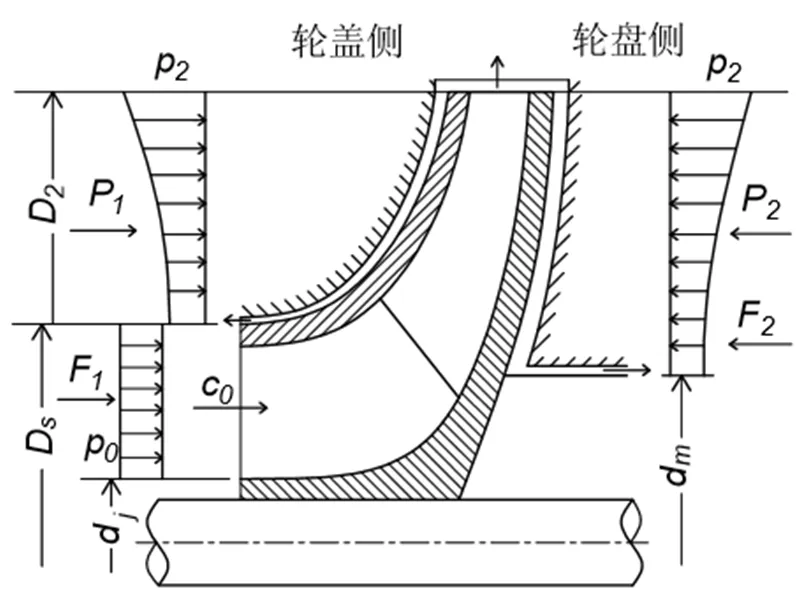
图1 叶轮轴向力分布示意图

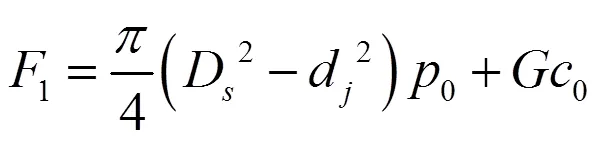
轮盘侧：气体压力在D至d间产生的轴向力为：

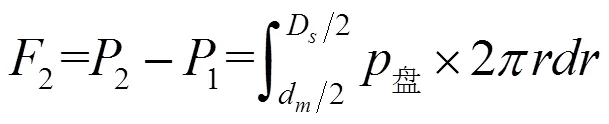
其中，

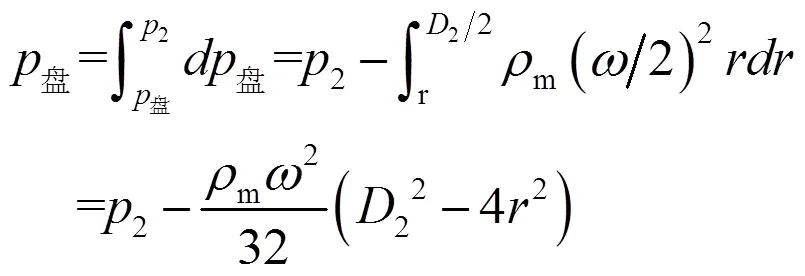
经过推倒整理，整个叶轮的气体轴向力为：

将设计工况下的数据（进口压力0为342.9kPa，出口压力2为570kPa，密封直径d为60mm）代入上述公式，算得轴向力：

即轴向力大小为644.9N，方向由轮盖侧压向轮盘侧。

2 数值计算方法

2.1 模型构建

抽取流体域作为物理模型，包含叶轮模型和泄漏模型（如图2所示）。泄漏间隙进口密封处和密封直径处泄漏间隙为0.2mm，其余处为1mm。

图2 叶轮和泄漏模型

2.2 网格划分

对叶轮单流道进行六面体结构化网格划分，网格数为212976。由于泄漏区域圆周对称，只取十六分之一模型进行分析，对其进行四面体非结构化网格划分，通过网格独立性验证，网格数为838898。

2.3 计算参数与边界条件设置

本文计算的气悬浮离心压缩机包括叶轮流道和泄漏通道两部分，如图3所示。设置叶轮部分为旋转计算域，设置转速分别为18000r/min、21000r/min、24000r/min。泄漏部分为静止计算域。流体设置为R134a，参考压力为0Pa，热量传输模型为Total Energy，湍流模型采用标准-模型。叶轮周期和泄漏周期均采用周期性交界面，叶轮和泄漏之间的交界面采用冻结转子模型。

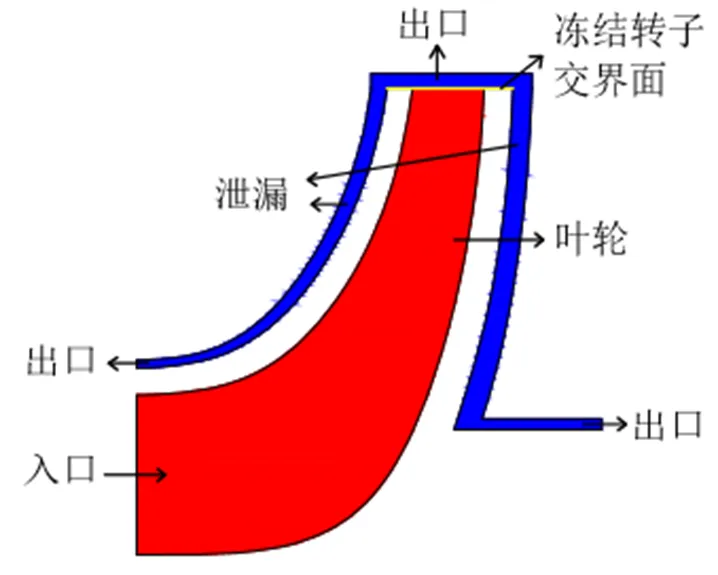
图3 叶轮和泄漏部分计算模型简图

采用总压入口和静压出口边界条件。入口总压为355.78kPa，入口总温为6.5℃，出口静压根据不同的工况设置。轮盖、轮盘和叶片表面均设置为无滑移、光滑、绝热壁面。泄漏部分内表面为旋转壁面，外表面为静止壁面。采用一阶迎风离散格式，设置残差为1.0E-5。

2.4 压力分布

选取进口总压为355.78kPa，出口流量分别为2.8kg/s、2.4kg/s、1.6kg/s的三种工况下，对叶轮轮盘、轮盖内壁面和叶轮轮盘、轮盖外壁面的压力分布进行分析。

出口流量为2.4kg/s时的轮盘外壁面的压力分布如图4所示，可以看出，轮盘外壁面的压力从中心沿径向逐渐增大。将三种工况下轮盘外壁面的压力随半径的变化绘制成图5，从图中可以看出，叶轮轮盘外壁面压力与半径近似呈线性关系。

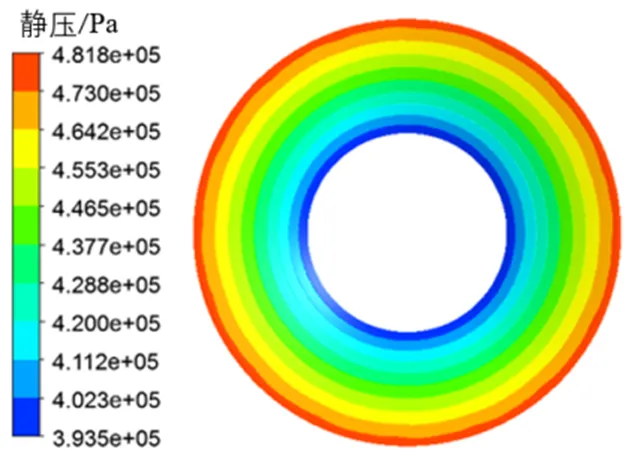
图4 叶轮轮盘外壁面的压力分布图

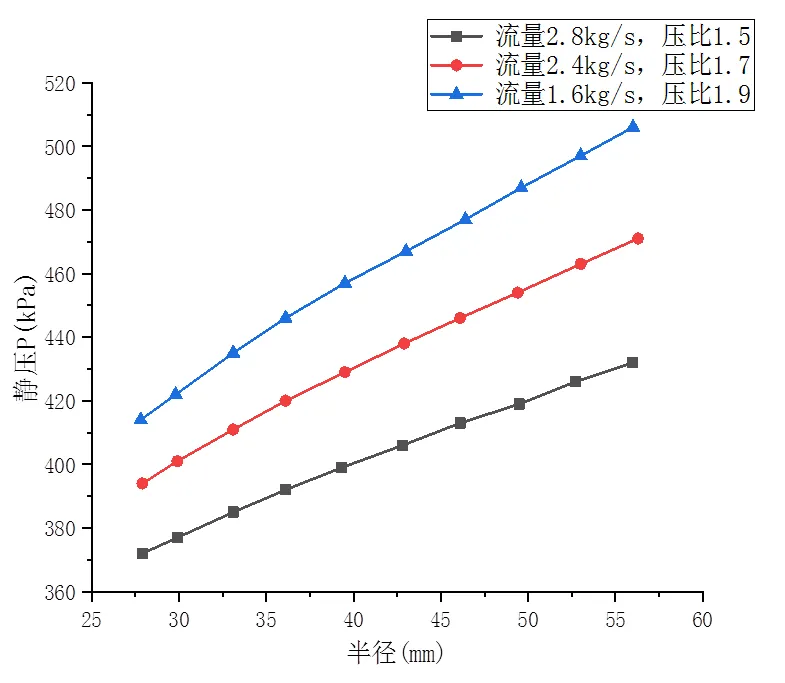
图5 叶轮轮盘外壁面的压力随半径的变化图

出口流量为2.4kg/s时轮盖外壁面的压力分布如图6所示，可以看出，轮盖外壁面的压力几乎也是从中心沿径向逐渐增大。并将这三种工况下轮盖外壁面的压力随半径的变化绘制成图7，从图中可以看出，当半径比较小时，即靠近进口处时，压力随半径变化得很快，当流过入口段时，压力随半径的变化减慢，且呈线性关系。

图4轮盘外壁面的压力变化范围为395.3kPa～481.8kPa，图6轮盖外壁面的压力变化范围为343.2kPa～471.9kPa，对比可以看出，叶轮轮盖外壁面的压力变化剧烈程度比轮盘的大。

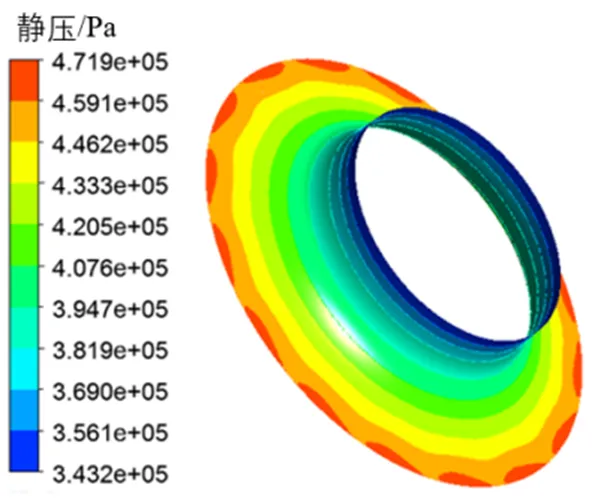
图6 叶轮轮盖外壁面的压力分布图

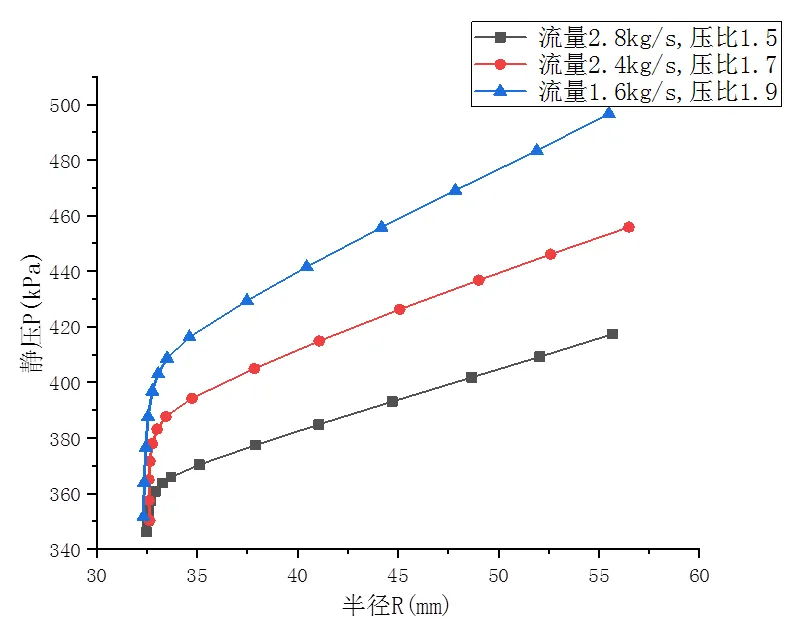
图7 叶轮轮盖外壁面的压力随半径的变化图

轮盖内壁面的压力分布如图8所示，从图中可以看出，在叶轮流道内，气体压力变化剧烈，但气体从进口流到出口，压力并不是一直增大的，而是先减小再不断增大。这是因为在进口处，由于进气通道的抽吸作用，气体的压力有所降低，随着气体的流动，压缩机对气体做功，压力逐渐升高，在出口处达到最大[16]。

图8轮盖内壁面的压力变化范围为196.6kPa～464.2kPa，图9轮盘内壁面的压力变化范围为292.6kPa～455.1kPa，对比可以看出，叶轮轮盖内壁面的压力变化剧烈程度比轮盘的大。

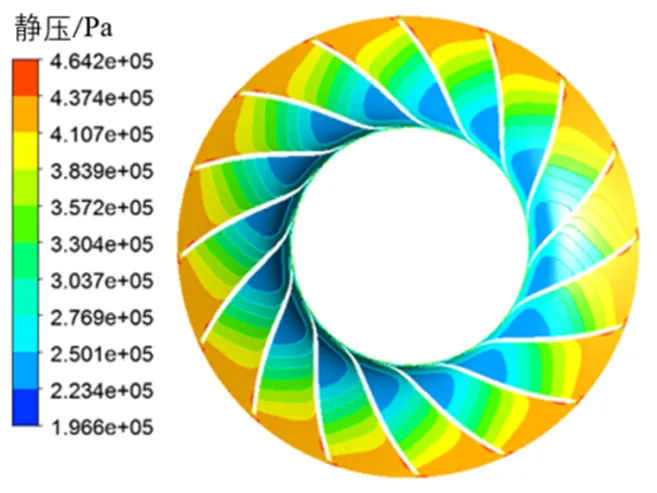
图8 叶轮轮盖内壁面压力分布图

图9 叶轮轮盘内壁面压力分布图

2.5 轴向力计算结果分析

由于本文数值模拟中只对流体区域进行了计算，所以计算轴向力时忽略了轮盖进口壁面所受的轴向力。针对设计工况，由公式=0计算得轮盖进口壁面所受轴向力为147.9N，CFD数值计算中得到的叶轮轴向力为526.7N，两者相加得到的总轴向力为674.6N。

上节理论计算得到的轴向力为644.9N，方向都是由轮盖侧压向轮盘侧。因此，数值计算与理论计算的误差为4.4%。由此可以验证，数值计算结果具有一定的准确性。

钟瑞兴等人[17]对离心压缩机轴向力进行的试验研究表明，其轴向力理论计算结果与试验结果误差小于5%，说明理论计算可以为离心压缩机轴向力设计提供理论依据。Shi Weidong等人[18]使用数值模拟来预测深井泵的轴向力，模拟结果与测量值的比较表明，在整个操作条件范围内，误差为0.3～5.9%。

CFD数值计算结果与理论计算值和试验测量值的误差都较小，因此数值计算结果具有一定的准确性，可作为离心制冷压缩机轴向力计算的一种可靠方法。

3 结果分析

3.1 压缩机特性曲线

离心压缩机特性曲线反映了离心压缩机变工况性能，它清晰的表明了各种工况下压缩机的性能、稳定工作范围等，是压缩机运行控制、分析变工况性能的重要依据[19,20]。本文采用CFD数值方法计算了三种不同转速下的压缩机特性曲线，如图10所示。

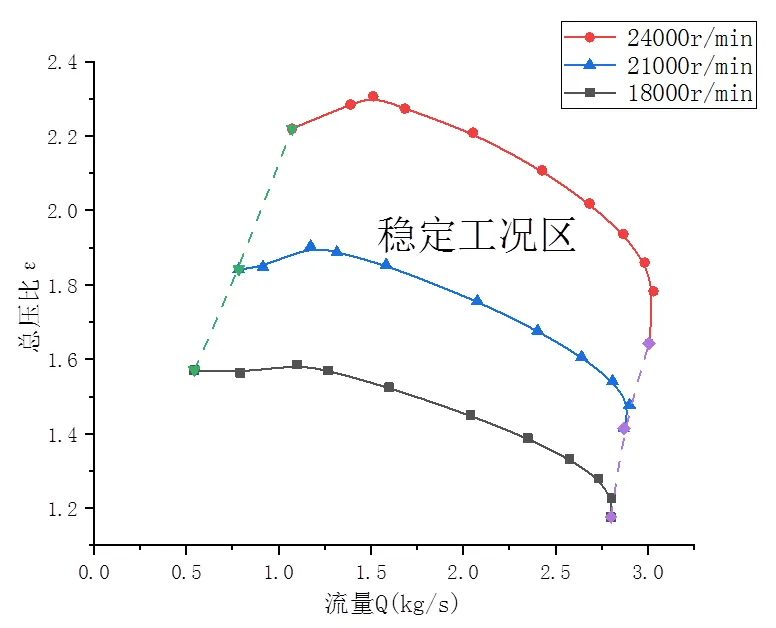
图10 离心压缩机特性曲线

压缩机某一转速下，有一定的稳定工况范围。当流量减小到一定值时，压比开始下降，此时接近喘振区；当流量增大到一定值时，压比快速下降，此时接近阻塞区。

3.2 轴向力影响因素

从叶轮轴向力计算公式（4）中可以看出，对叶轮轴向力的影响有压缩机运行工况和叶轮结构参数，其中：运行工况对轴向力的影响有进口压力、出口压力和流量，并且进、出口压力对其影响较大；结构参数密封直径d对轴向力具有较大影响。

3.2.1 变工况的影响

设置进口总压为355.78kPa，改变出口静压值，得到18000r/min、21000r/min、24000r/min三种转速下，叶轮轴向力随工况的变化趋势（见图11）。

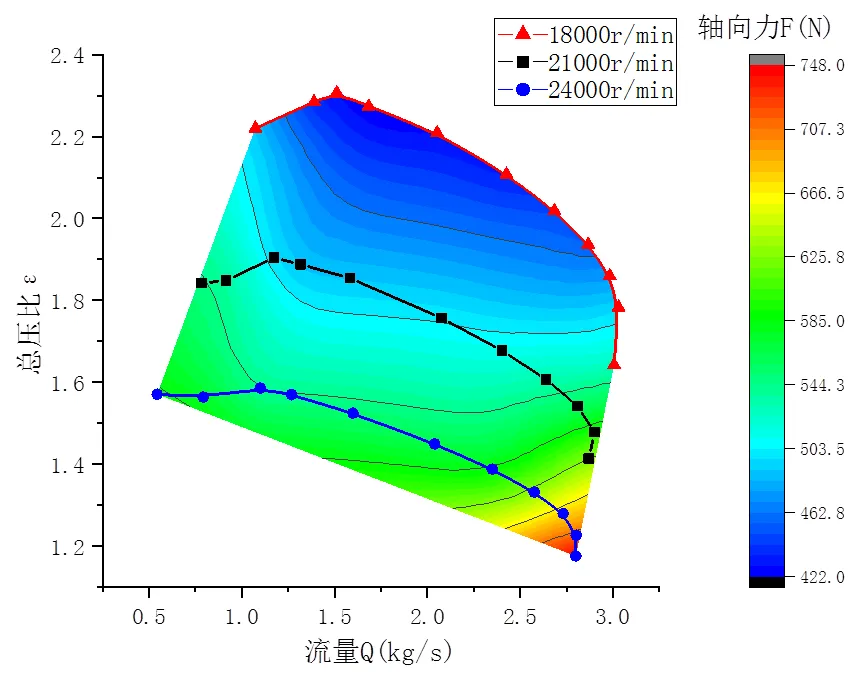
图11 叶轮轴向力随流量-总压比变化图

从离心压缩机特性曲线中可以看出，总压比是随着流量的变化而变化。因此当压比变化对轴向力产生影响时，流量也会对轴向力产生影响，也就是流量和压比共同对叶轮轴向力产生影响。

取入口流量为2kg/s，将此流量下的转速，总压比，轴向力绘制成表1，可以看出，在流量相同时，转速越大，总压比越大，轴向力越小。

表1 流量为2kg/s时转速、总压比、轴向力变化

当叶轮转速为18000r/min时，稳定工况区内的轴向力变化范围为542N～747N；当叶轮转速为21000r/min时，稳定工况区内的轴向力变化范围为489N～627N；当叶轮转速为24000r/min时，稳定工况区内的轴向力变化范围为422N～526N。

本文计算工况下，最大轴向力是设计工况下轴向力的1.4倍，最小轴向力是设计工况下的0.8倍。

在18000r/min、21000r/min、24000r/min这三种转速下，叶轮轴向力随流量变化如图12所示。当压缩机工作点位于工作区时，叶轮轴向力随流量的减小而增减小，但当流量减小到接近喘振流量时，轴向力又开始增大。

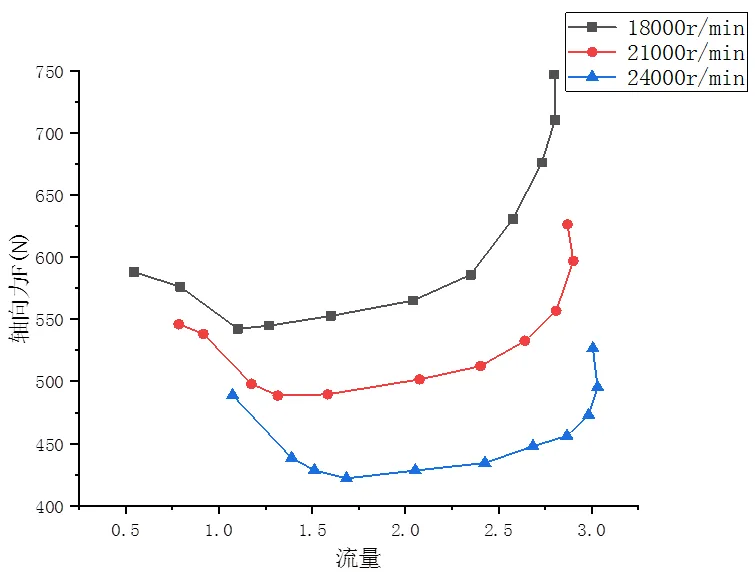
图12 叶轮轴向力随流量变化图

当压缩机工作点接近喘振区和阻塞区时，叶轮所受的轴向力较大。所以，应严格控制压缩机的运行工况，使压缩机工作点远离喘振区和阻塞区，可防止轴向力过大造成轴承损害。

3.2.2 密封直径的影响

在进口总压为355.78kPa，出口静压为342.9kPa，转速为21000r/min的条件下，改变密封直径d的大小，分别设置为40mm、42mm、44mm、60mm，对其进行模拟，得到的轴向力大小如表2所示。由此可以得到当密封直径d为44mm时，叶轮所受轴向力最小。

表2 不同密封直径下的轴向力

4 结论

本文以离心压缩机闭式叶轮为研究对象，采用CFD数值方法对叶轮进行轴向力模拟，详细分析了压比、流量、转速、密封直径等参数对轴向力的影响，得到如下主要结论：

（1）通过对叶轮轴向力数值计算结果与理论计算结果的对比，计算误差约为4.4%，验证了数值模型的准确性。

（2）轮盘外壁面的压力从中心沿径向逐渐增大，且与半径近似呈线性关系；气体在叶轮内的压力先减小后逐渐增大；轮盖侧的压力变化剧烈程度比轮盘侧的大。

（3）当压缩机运行工况位于稳定工况范围时，叶轮轴向力随压比的增大而减小，随流量的减小而减小，但当压缩机运行工况接近喘振区和阻塞区时，轴向力明显增大；叶轮轴向力随转速的增大而减小；本文计算工况下，最大轴向力是设计工况下轴向力的1.4倍，最小轴向力是设计工况下的0.8倍；本文计算条件下，当密封直径d为44mm时，叶轮所受轴向力最小。

[1] 陈文卿,马元,彭学院,等.制冷压缩机基础理论研究与关键技术开发[J].制冷学报,2010,31(4):14-21.

[2] 程伟,屈福康,肖金,等.基于Flow Simulation的高风压离心式风机设计[J].制冷与空调,2019,33(3):283-286.

[3] 罗定鑫,张瑞,李镇杉,等.水平对置式离心压缩机轴向力分析与测试研究[J].暖通空调,2019,49(4):145-148.

[4] JAPIKSE D. Centrifugal compressor design and performance [M]. Billings: Concepts ETL Inc, 1996:15-18.

[5] 李立.悬臂式高压离心泵轴向力计算及影响因素分析研究[D].西安:西安理工大学,2019.

[6] 张国军.透平膨胀机轴向力数值计算方法研究[D].兰州:兰州理工大学,2014.

[7] Cao W, Dai X, Hu Q, et al. Effect of impeller reflux balance holes on pressure and axial force of centrifugal pump[J]. Journal of Central South University, 2015,22(5):1695-1706.

[8] 姬忠礼,邓志安,赵会军.泵和压缩机[M].北京:石油工业出版社,2008:166-170.

[9] Anantachaisilp P, Lin Z. Fractional Order PID Control of Rotor Suspension by Active Magnetic Bearings[J]. Actuators,2017,6(1):1-31.

[10] 王东,姜豪,苏振中,等.船用磁悬浮轴承关键技术与发展综述[J/OL].中国电机工程学报:1-13[2020-06-19]. https://doi.org/10.13334/j.0258-8013.pcsee.200174.

[11] Schiffmann J A, Kontomaris K, Arpagaus C, et al. Scale limitations of gas bearing supported turbocompressors for vapor compression cycles[J]. International Journal of Refrigeration, 2020:92-104.

[12] 骆文平.气浮直驱高速离心风机关键技术研究[D].哈尔滨:哈尔滨工业大学,2015.

[13] 闻苏平,朱报桢,苗永淼.高压离心压缩机轴向推力计算[J].西安交通大学学报,1998,(11):3-5.

[14] 石建伟,金永鑫,宋文武,等.多级离心泵叶轮相位交错对转子受力变化的影响[J].热能动力工程,2017,32(11): 33-40,130.

[15] 黄钟岳,王晓放.透平式压缩机[M].北京:化学工业出版社,2004:124-126.

[16] 王净.高压比离心压气机叶轮冷却仿真研究[D].哈尔滨:哈尔滨工程大学,2015.

[17] 钟瑞兴,张治平,陈玉辉,等.离心压缩机轴向力计算与试验研究[J].制冷,2016,35(1):16-21.

[18] Weidong S, Hongliang W, Ling Z, et al. The Estimation and Experiment of Axial Force in Deep Well Pump Basing on Numerical Simulation[J]. International Journal of Modern Education and Computer Science, 2010,2(2):53-61.

[19] 吴业正,李红旗,张华.制冷压缩机[M].北京:机械工业出版社,2010:254-256.

[20] 张泽国,樊海彬,曹向军,等.不同型线的高效二元离心叶轮优化设计[J].制冷与空调,2013,27(1):65-69.

Axial Force Analysis of Centrifugal Refrigeration Compressor Based on Numerical Method

Yi Kexin Zhao Yuanyang Wang Chun

( College of Electromechanical Engineering, Qingdao University of Science and Technology, Qingdao, 266061 )

Centrifugal refrigeration compressors are widely used in commercial air-conditioning systems, and the gas suspension of rotor is an important development direction of centrifugal compressors in the future. But the bearing capacity of gas bearings, which bear the axial force on impeller, is smaller than that of traditional bearings. Therefore, the axial force of the shrouded impeller under full working conditions is simulated with the CFD numerical method. The numerical results are verified by the theoretical results. The influences of pressure ratio, flow rate, rotating speed, and seal diameter on the axial force are analyzed. The results show that when the compressor is operated in the steady working conditions, the axial force of impeller decreases with the increase of pressure ratio and the decrease of flow rate. But when the working point of the compressor is near the surge and the choked areas, the axial force of impeller increases. The axial force of impeller decreases with the increase of rotation speed.The error between the numerical calculation and theoretical calculation of the axial force under design conditions is only 4.4%, indicating that the CFD numerical method can be used as a reliable method for the calculation of the axial force of the centrifugal compressor impeller.

Centrifugal compressor; impeller; axial force; Gas suspension; CFD method

1671-6612（2021）03-371-06

TB652

A

衣可心（1996-），女，硕士，在读硕士研究生，E-mail：1215148207@qq.com

赵远扬（1978-），男，博士，教授，E-mail：yuanyangzhao@163.com

2020-10-14