基于β散度约束的非负矩阵分解的机械复合故障诊断方法*
2021-07-25王梦阳薛向尧邵明振
王梦阳,郭 劲,薛向尧,时 魁,邵明振,王 光,遇 超
(1.中国科学院长春光学精密机械与物理研究所,长春 130033;2.中国科学院大学,北京 100049)
0 引言
非负矩阵分解(NMF)是一种新的特征提取方法,由于分解前后的矩阵中仅包含非负的元素,在某种意义上抓住了智能数据描述的本质,使其分解结果更具物理意义[1]。由于算法的简便性,特征信息的局部性[2],因而在生物医学工程、模式识别、图像目标提取等方面应用广泛[2]。
随着算法的不断推广,有学者将NMF算法应用在盲源分离的问题上。相较于传统解决盲源分离采用的独立分量分析和稀疏分量分析算法,非负矩阵分解算法分解形式简单,收敛较快[3],效率更高。武健[4]提出了基于非负矩阵分解的盲分离算法,实现了心电信号的有效分离。Hao Yansong等[5]采用内稟特征尺度分解与LNMF算法结合,实现了多源信号的欠定盲源分离。王梦阳等[6]提出了基于EVMD-LNMF的复合故障信号分离方法,通过引入能量收敛因子,成功分离出多源故障信号。王宏超[7]将稀疏约束作为非负矩阵分解算法的惩罚函数,通过引入反馈机制,有效解决了欠定盲分离问题。然而在实际工况下的旋转机械领域,由于运行环境嘈杂,滚动轴承产生的振动信号十分复杂,特征信息通常淹没在噪声中,难以提取。综上,本文采用β散度约束作为非负矩阵分解算法的惩罚函数,通过构建新指标加权脉冲因子(Correlation impulse factor.CIF),筛选分解后的重构信号。从而有效分离提取出耦合故障特征,实现机械的复合故障诊断。
1 β-NMF算法模型
非负矩阵分解的算法模型[8]可简单地定义为:对任意的非负矩阵,NMF算法总能够找出非负矩阵和,使其满足:

式中:m为矩阵的维数;n为样本个数;r为矩阵的秩。
自NMF算法提出以来,已有大量研究针对其惩罚函数进行优化改进,如α散度约束、β散度约束、Bregman散度约束等。而NMF算法固有的惩罚函数取决于应用领域及数据处理类型[9]。本文根据实际轴承发生复合故障时信号之间的相互耦合,信噪比低,导致重构信号很难表达多源故障特征信息。为此,选择数据适应性更强的β散度作为NMF算法的惩罚函数,其表达式为:
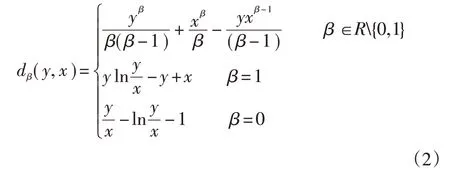
而将β散度约束作为NMF算法的目标函数可用下式表示:

根据迭代算法,循环迭代矩阵W和H,直至式(3)目标函数收敛,停止迭代,输出矩阵W和H。
2 基于β-NMF算法的复合故障诊断方法
2.1 加权脉冲因子
脉冲因子指标可以作为信号处理领域中检测有无冲击成分,其定义为信号的峰值与整流平均值的比值。相关系数指标定义为信号之间的相关程度。本文根据故障时信号的冲击特征及重构后信号的选取规则,构建信号的综合影响参数加权脉冲因子(Correlation impulse fac⁃tor.CIF),其定义如下:
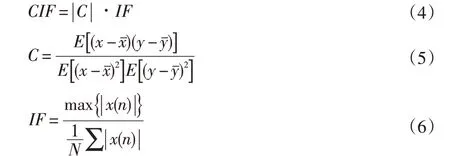
式中:IF(impulse factor)为信号x(n)的脉冲因子;N为信号选取的长度;C为信号之间的相关系数。
由相关系数的性质可知,|C|≤1。因此,C可以看作是脉冲因子的权重,故参数CIF定义为加权脉冲因子。
2.2 基于β-NMF的复合故障诊断方法
综上,针对实际滚动轴承出现耦合故障时产生的振动信号,本文提出了基于β散度约束的非负矩阵分解的机械复合故障诊断方法。方法流程如图1所示,步骤如下:
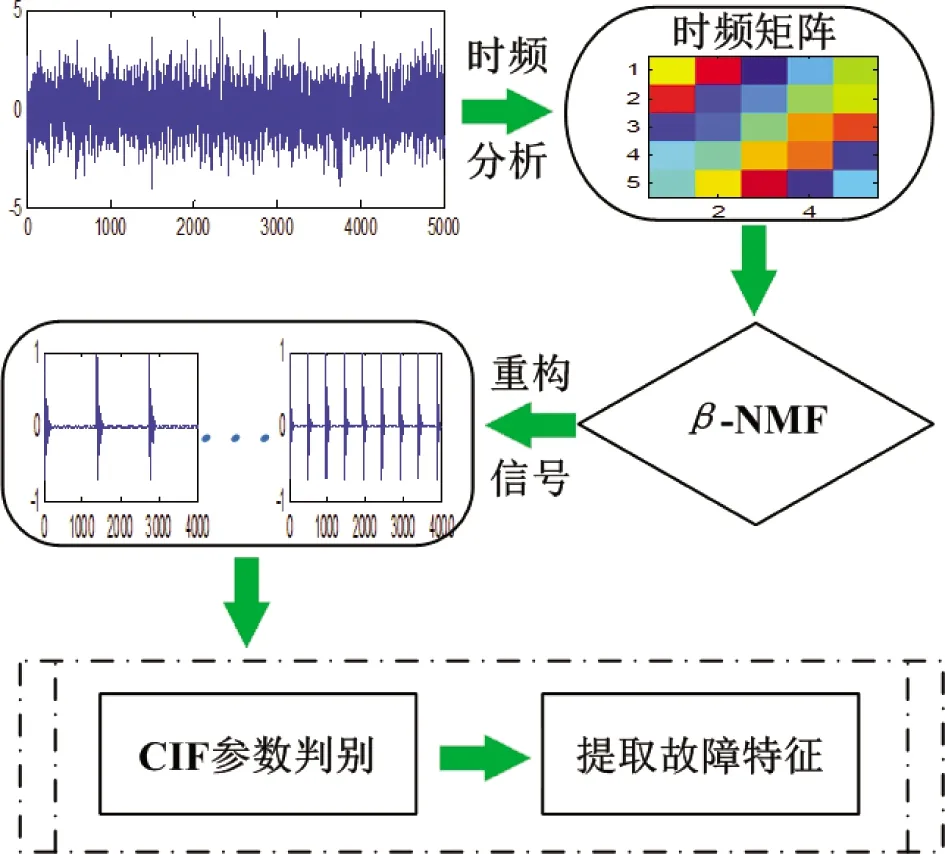
图1 诊断方法流程Fig.1 Flow chart of method about fault diagnosis
(1)对采集的振动信号进行时频分析,得到时频特征矩阵;
(2)取时频矩阵的能量值,采用β-NMF算法分解处理,并将分解后的向量在时域中恢复;
(3)计算恢复信号的CIF参数值;
(4)选择参数CIF值较大的恢复信号,作其包络频谱图,从频谱图中提取相应的特征信息,完成故障诊断。
3 仿真信号分析
为了说明所提出方法的有效性,采用如下的模型来模拟滚动轴承发生故障时产生的振动信号:
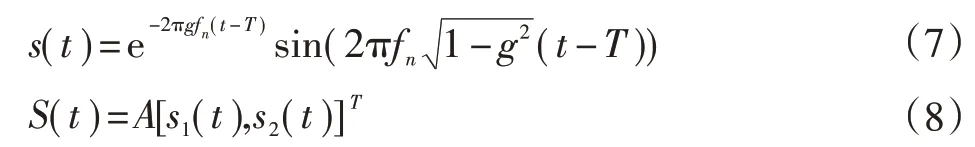
式中:g为阻尼属性,本文取值0.1;s1(t)和s2(t)为模拟故障信号,按fn分别取3 500 Hz和5 500 Hz。
由式(7)中s(t)的形式,可知产生的特征频率为f=1/T,本文取值63 Hz和157 Hz。采样频率取fs=100 kHz,截取0.5 s时间片段作为仿真分析数据。随机产生混合矩阵A=[0.857 3,0.942 6],按照式(8)形式获得信号S(t)。对信号S(t)作归一化处理,得到其时域波形和包络频谱如图2所示。
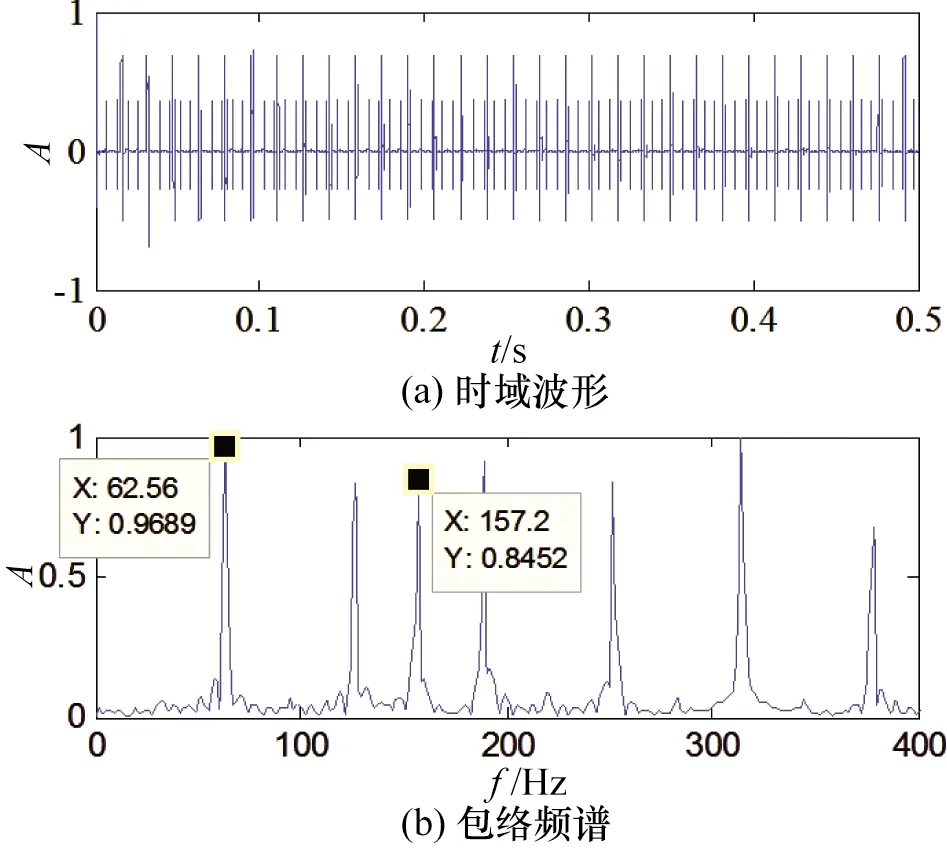
图2 仿真信号的时域波形和包络频谱Fig.2 Waveform and envelope spectrum of simulated signals
根据图1中的流程步骤,采用所提出的方法对上述仿真信号进行分析。首先对混合信号S(t)进行时频分析,获得高维时频特征矩阵;其次取时频特征矩阵的能量值,采用β-NMF算法分解降维,将分解得到的特征分量在时域中恢复还原;然后计算恢复后信号的CIF参数值,如表1所示。由表可知,筛选出第8组与第9组的CIF参数值。对筛选出的二组信号作归一化处理,其包络频谱图如图3所示。
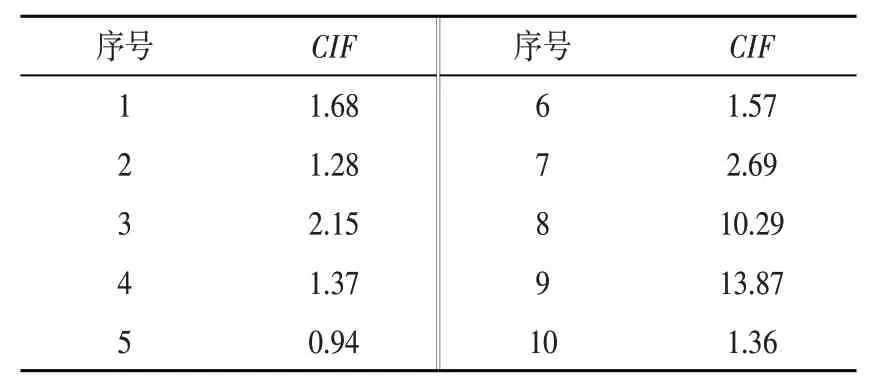
表1 恢复信号的CIF值Tab.1 CIF of the signal
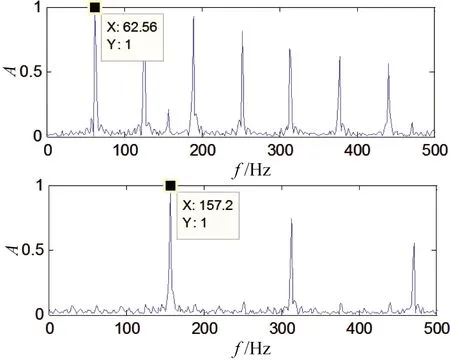
图3 分离后信号S(t)的包络频谱Fig.3 Envelope spectrum of the separated signals
由分离信号包络频谱图中可以看出,存在于仿真信号S(t)的两种特征成分63 Hz与157 Hz,经本文所提出的方法处理后可以有效分离。因此,从上述仿真信号的处理分析中,可以得出如下结论。原始混合信号经本文所提出的方法处理后,可以分离得到源信号,信号的特征信息也可以从频谱中提取出,验证了方法的有效性。
4 实验验证
本实验采用NTN N204型号的圆柱滚子轴承为研究对象,对其外圈和滚动体上加工相应缺陷。将此故障轴承安装在轴承座上,并在轴承座的竖直方向和水平方向上安装加速度传感器。将电机转速设为900 r/min,采样频率为100 kHz,采样时间为10 s。根据如表2所示的轴承相关参数计算得知滚动体故障特征频率fb=74 Hz,外圈故障特征频率fo=60 Hz。

表2 轴承NTN N204参数Tab.2 Structure parameters of bearing NTN N204
随机截取0.4 s数据片段的实测信号进行处理分析,对其进行归一化,得到时域波形和包络频谱如图4所示。由图可知信号明显存在冲击成分,表示此轴承已存在缺陷。在其包络频谱图中,特征信息被噪声成分淹没,难以作出相应识别诊断。
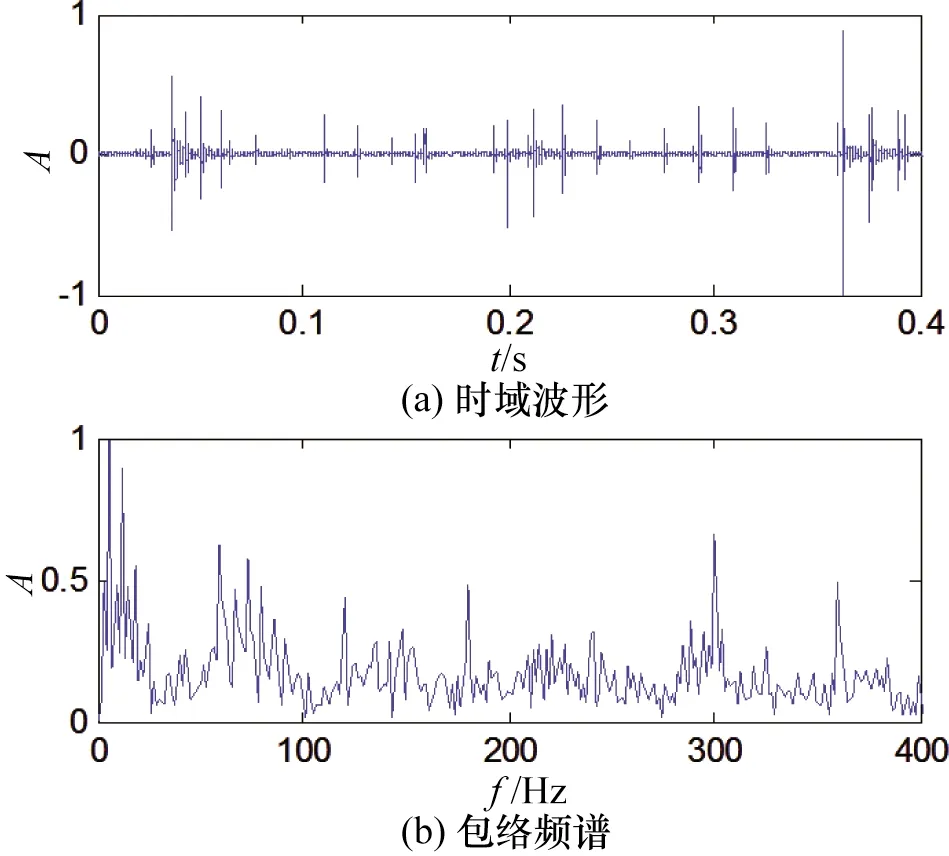
图4 实测信号的时域图和包络频谱Fig.4 Waveform and envelope spectrum of the signal
根据图1流程步骤,采用本文所提出的方法对采集的信号进行验证。首先对原始信号进行时频分析,获得高维时频特征矩阵;其次取时频特征矩阵的能量值,进行β-NMF算法分解降维,将分解得到的特征分量在时域中恢复还原;然后计算恢复后信号的CIF参数值,如表3所示。由表可知,第3组与第6组的CIF值较大。
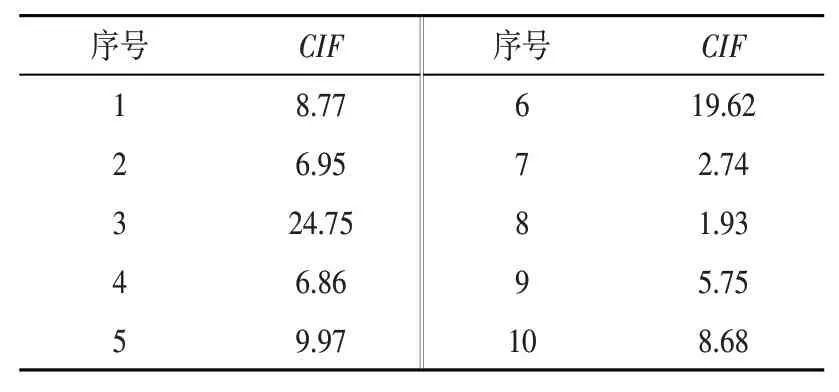
表3 恢复信号的CIF值Tab.3 CIF of the signal
对筛选出的二组信号作归一化处理,其包络频谱图如图5所示。由图可以看出,原始振动信号经过本文所提方法处理后,分离出两种源信号成分。通过与理论计算值对比,两种特征成分分别对应滚动体故障特征和外圈故障特征,并且出现了高次谐波成分也证明特征信息正确。实验结果表明,本文所提出的方法可以有效地从耦合信号中分离出故障源信号,在频谱图中也可以提取出故障特征频率信息,验证了该方法在轴承复合故障诊断中的有效性。
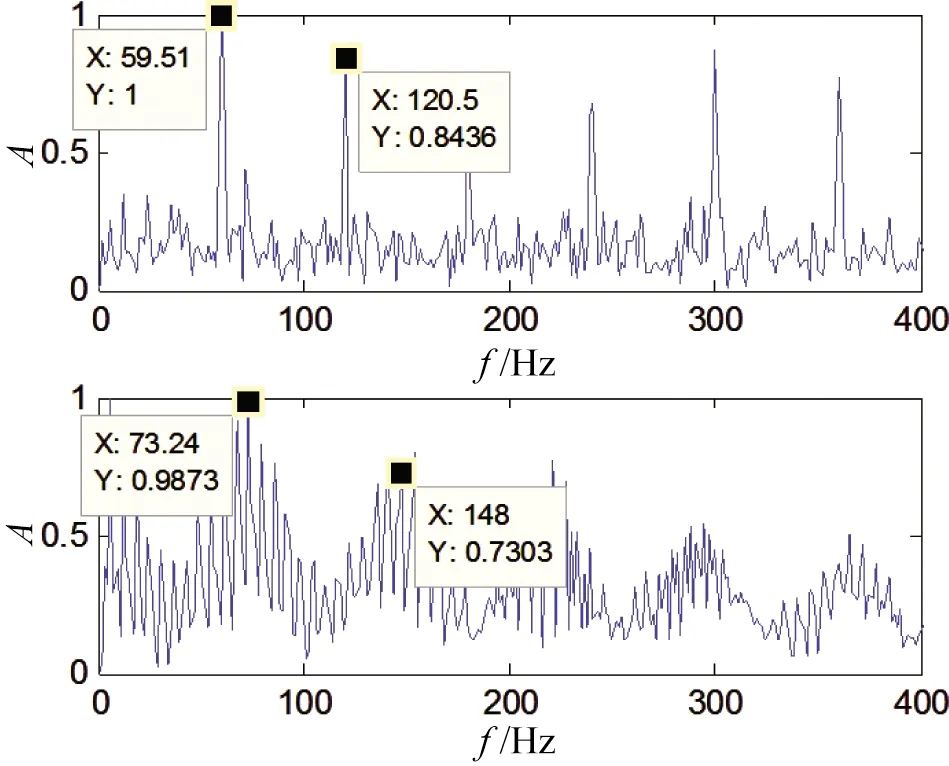
图5 分离信号频谱Fig.5 Spectrum of separated signals
5 结束语
本文针对机械故障诊断领域中存在耦合故障、特征信息难以识别提取的问题,提出了基于β散度约束的非负矩阵分解的机械复合故障诊断方法。利用数据适应性更强的β散度约束,增强局部分解能力;并通过在算法中引入加权脉冲因子(CIF),对重构后的信号进行筛选,有效地减少了分解后的冗余信息,实现了数据的有效降维。将其应用在实际滚动轴承信号中,表明存在多重缺陷的故障轴承,经本文所提出的方法处理后,可以分离提取出其特征信息,实现了机械复合故障的有效诊断。因此,本文提出的方法在机械故障诊断领域具有一定的参考意义和工程应用价值。
