过载振动复合条件下的加速度计不对称性误差分析

关伟

(国营长虹机械厂,广西 桂林 541002)

0 引言

导弹、火箭等飞行载体上的加速度计工作时一般都会经受大量级过载与振动复合作用的环境,振动整流误差成为在过载-振动复合环境下衡量加速度计性能的重要指标。振动整流误差的产生与加速度计结构和电路有关[1-2],是加速度计的固有特性。振动整流误差表现为加速度计输出的时域信号平均值中直流量的异常漂移[3],当振动加速度作用时,从常用的加速度计误差模型来看,振动整流误差的主要来源包括加速度计不对称性(包括偏值不对称性和标度因数不对称性)和偶次非线性项(即加速度计误差模型中的二次项、四次项等误差项)[4-5]。2005 年有学者研究了过载振动复合环境下的惯性仪表误差建模方法[6];2013 年有学者将复合环境下的整流误差用于校准加速度计的非线性系数[7];2014 年则有人通过仿真证明了过载振动复合环境下振动整流误差取决于过载和振动的共同作用[8]。在2015 年,董雪明等人则提出了加速度计振动整流误差的校准方法[9]。目前过载-振动复合环境下整流误差的研究主要是与加速度计模型中的二阶及以上非线性项有关,尚未研究复合环境下加速度计不对称性对整流误差的影响。

加速度计不对称性是指在方向相反的输入加速度激励下,加速度计零偏和标度因数的不一致性。随着加速度计准确度的提升和量程的增大,加速度计不对称性引入的误差将更加明显和重要[10]。本文首先建立过载振动复合环境下包含加速度计不对称性的加速度计振动整流误差模型,之后通过模型和仿真分析加速度计不对称性对振动整流误差测试结果的影响,最后给出分析结论。

1 加速度计误差模型

对大多数加速度计而言,在考虑加速度计不对称性误差时,加速度计的输出可以表示为[2,4]

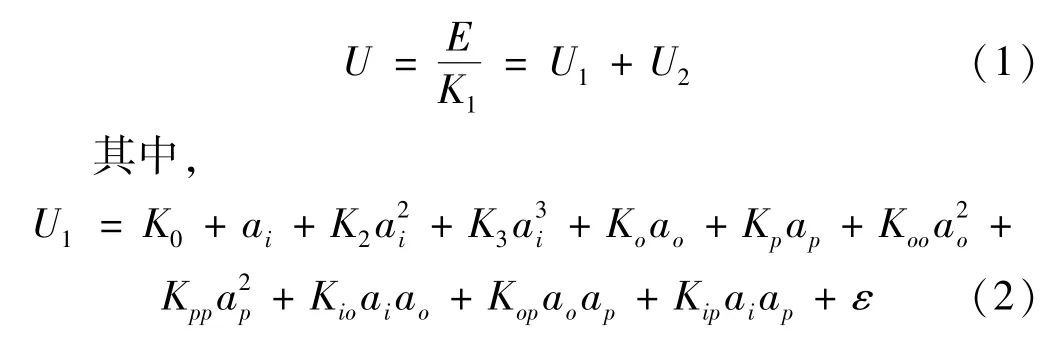
加速度计不对称性项表示为

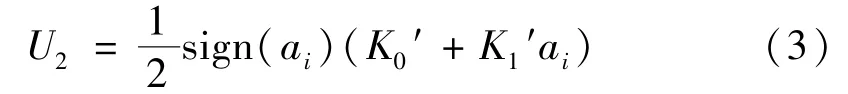
式中:E为加速度计输出,为表示方便,以伏特(V)表示;U为加速度计输出,g;K0为偏值,g;K0′为偏值不对称性,g;K1为加速度计标度因数,V/g;K1′为标度因数不对称性,无量纲;K2为二阶非线性系数,g/g2;K3为三阶非线性系数,g/g3;Kp,Ko为交叉轴灵敏度,V/g;Kpp,Koo为交叉轴非线性系数,g/g2;Kio,Kip为交叉耦合系数,g/g2;ai,ao,ap分别为沿加速度计输入轴(IA),输出轴(OA)和摆轴(PA)的加速度,g;sign (ai) 为符号函数,sign (ai)=ε为均值为0 的测量噪声,包括信号噪声以及未建模误差。

由于加速度计误差模型中的四次项系数量级很小,本文并未将其纳入模型方程。

2 振动整流误差模型

一般采用给定频率和幅值的正弦振动激励加速度计,通过对比加速度计在静止和振动两种状态下的输出信号整周期算术平均值来得到振动整流误差。将加速度计三个轴上的加速度分量统一表示为

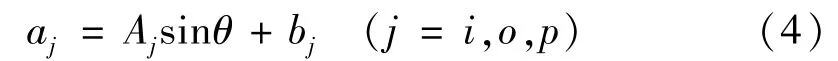
式中:Ajsinθ为加速度分量中的振动加速度,θ∈[0,2π];Aj为振动加速度幅值,g;bj为过载,g。

本文主要分析加速度计不对称性的影响,由式(3)可知,U2与沿OA,PA输入的加速度无关。一般的整流误差测试主要采用输入轴处于水平状态的标定方法,不能体现同一方向复合加速度对整流误差的影响[11]。为便于讨论,按图1 所示坐标系安装加速度计,使得IA与振动方向位于竖直面,而OA和PA位于水平面。

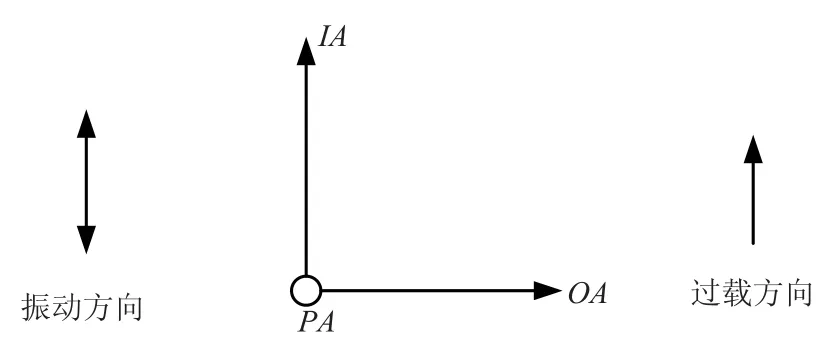
图1 加速度计安装坐标系

当加速度计静止时,各轴加速度分量为

当加速度计振动时,加速度计各轴加速度分量为

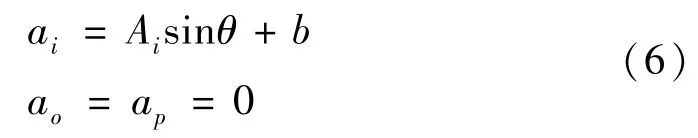
不失一般性,假设b >0,接下来分两部分讨论。

2.1 高阶非线性项引起的整流误差

对式(2)所示U1对应的时域信号,在加速度计静止时,其算术平均值为

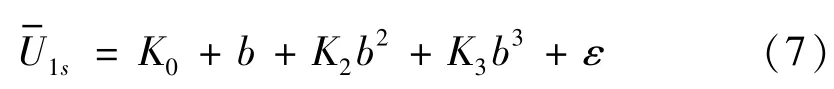
在加速度计同时受到过载与振动激励时,其算术平均值为

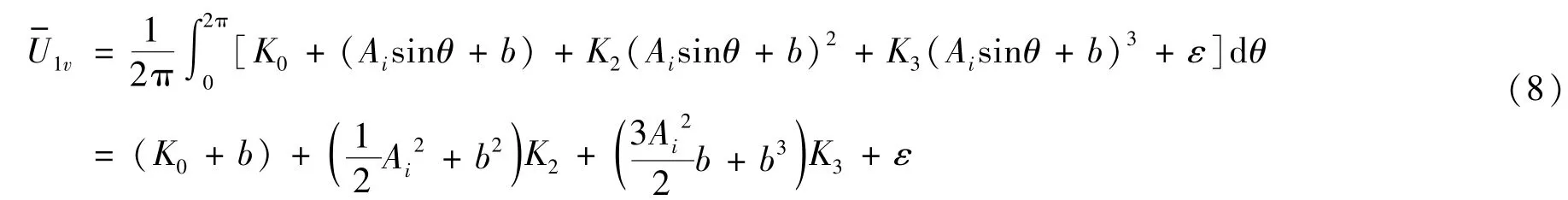
U1对应的整流误差为

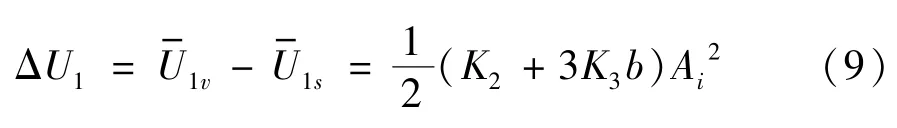
由式(9)可知,该部分整流误差与加速度计高阶非线性项系数(K2和K3)有关。

2.2 系数不对称性引起的整流误差

对式(3)所示U2对应的时域信号,在加速度计静止时,其算术平均值为

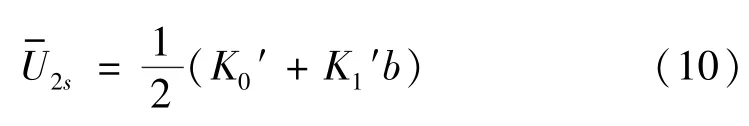
在加速度计同时受到过载与振动激励时,其对应的时域信息表达式为

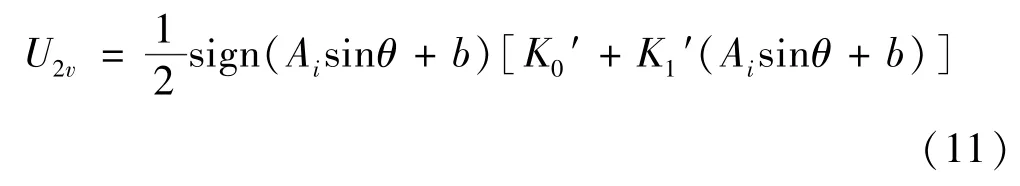
根据振动加速度幅值与过载之间的关系,对U2v的整周期算术平均值分两种情况讨论。

即也可以忽略U2引起的振动整流误差。

综上所述,考虑了加速度计不对称性之后,在过载振动复合环境下的加速度计振动整流误差可表示为两部分之和

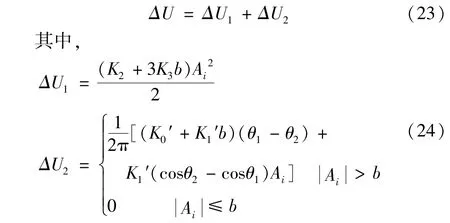
由式(24)可知,ΔU1和ΔU2与振动幅值、过载成正比,且ΔU2与振动幅值与过载的比值有关。

3 数值仿真分析

表1 仿真参数设置

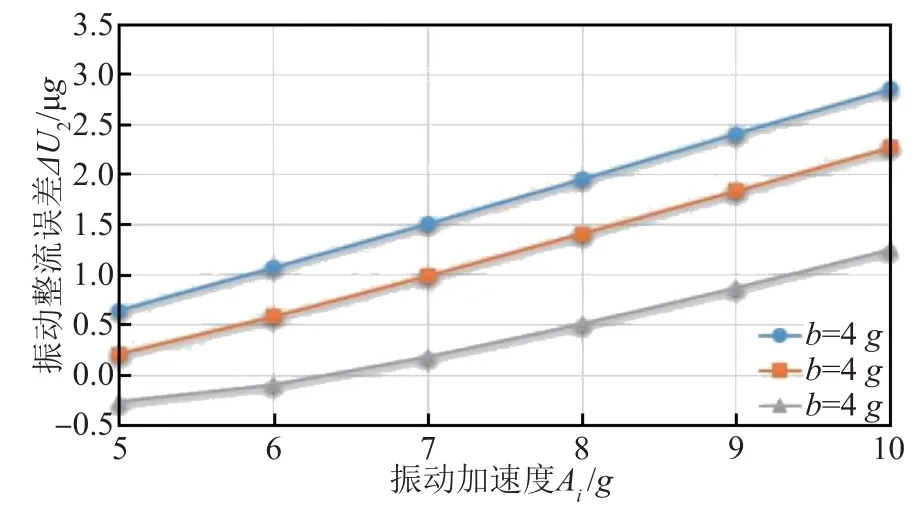
图2 加速度计不对称性引起的振动整流误差

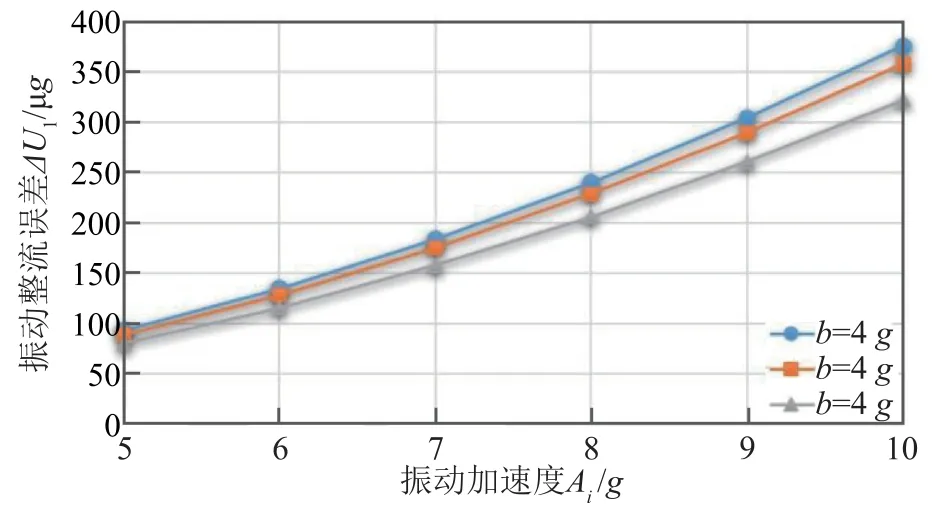
图3 高阶非线性项引起的振动整流误差

根据图2 和图3 可知,给定振动加速度和过载,由高阶非线性项引起的振动整流误差(ΔU1)是由加速度计不对称性引起的振动整流误差(ΔU2)的100 倍以上。定义振动整流误差测试相对误差为

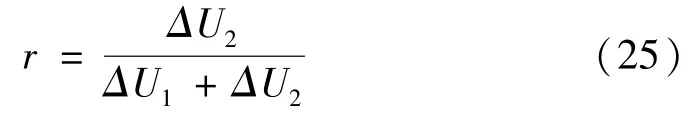
由图4 可知,由加速度计不对称性引起的测试相对误差小于1%。

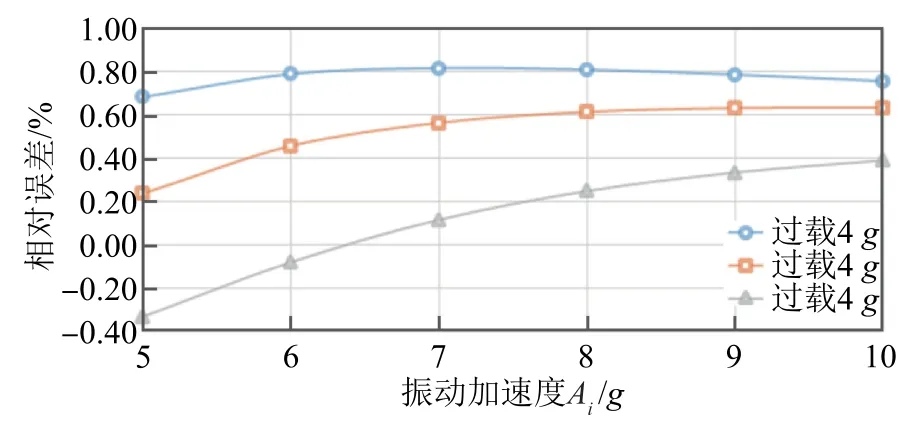
图4 加速度计不对称性引起的相对误差

当过载为1g时(重力加速度),若振动加速度为5g和6g,由加速度计不对称性引起的测试相对误差为负值,说明此时能够抵消部分因加速度计高阶非线性项引起的振动整流误差,从而减小总的振动整流误差。

4 结论

通过数学建模和仿真分析表明,加速度计不对称性影响整流误差测试准确度。

当加速度计敏感轴方向同时存在振动加速度和过载时,若振动加速度幅值不大于过载,则可忽略加速度计不对称性对整流误差测试的影响。在某些飞行器的主动段,一般满足此要求。

当振动加速度幅值大于过载时,根据仿真数据,加速度计不对称性引起的振动整流误差小于加速度计高阶非线性项引起的振动整流误差约2 个数量级。当加速度计在高振动环境下进行高准确度过载测量应用时,应考虑这种影响。

本文提供的分析思路可用于其他量级的振动加速度和过载组合,也适用于多轴加速度计的振动整流误差分析