光学遥感卫星几何成像模型高精度对地定位技术研究

赵巨波

（92941部队，辽宁葫芦岛，125000）

0 引言

随着科技的进步，现代卫星遥感技术得到了质的飞跃，高分辨率对地观测系统已成为地理空间信息获取的重要手段。现代卫星遥感技术已经成为国民经济与国防建设的重要标志，因此如何利用卫星影像精确获取目标的三维信息就会出现影响卫星影像的高精度定位。文章介绍了几何成像模型高精度对地定位技术，该技术是获取各种地理空间信息的基本保障，同时也是扩大高分辨率遥感卫星影像应用的重要前提和手段[1]。

1 光学遥感卫星影像成像所涉及的坐标系及其相互转换

坐标系及其转化在光学遥感卫星影像成像几何模型构建中起到了重要作用，卫星影像的像点与对应地面点的投影关系需要依靠坐标系间的转化进行计算，在实际操作中常用的几何模型坐标系有一下几种。

1.1 扫描坐标系

如图1所示为扫描坐标系，该坐标系（O、-X、J）通常使用行列号来表示像元素。对于遥感卫星影像来说，左上角第一行第一列为影像原点，若像元位于第X行第J列，则该像元的扫描坐标为（X，J）。

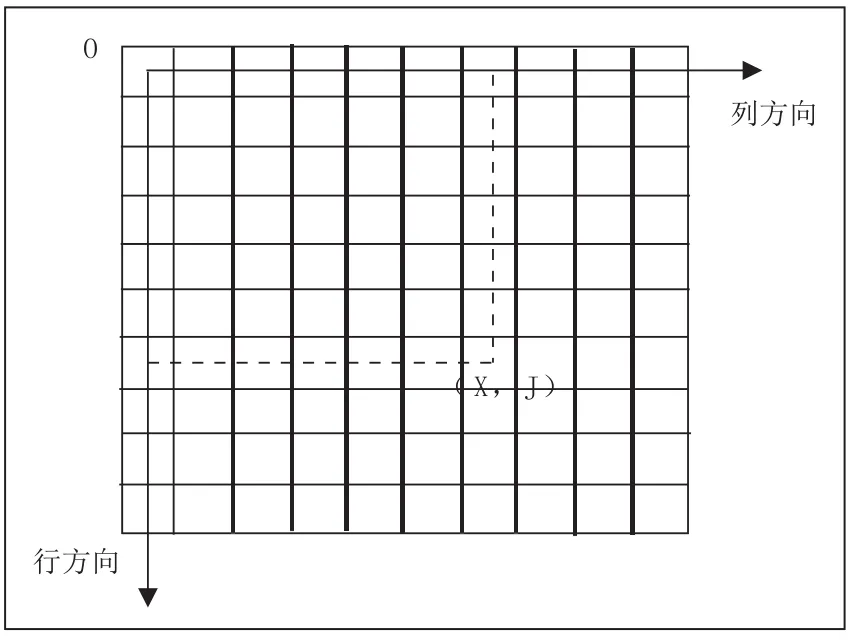
图1 扫描坐标系

1.2 瞬时影像坐标系

如图2所示为瞬时影像坐标系，其原点是每个扫描点的中心点，用（O-xy）来表示瞬时影像坐标系。该坐标系下的遥感卫星的像点为（o，y），因此x轴即为卫星的飞行方向，y轴即为扫描方向[2]。

图2 瞬时影像坐标系

1.3 传感器坐标系

如图3所示为传感器坐标系,同时也被称为相机坐标系（OC-XCYCZC）。该坐标系的原点为传感器的投影中心，XC轴、YC轴与影像的轴线相平行，ZC根据右手法则定律来划分，因此在传感器坐标系下卫星影像的像点为（x，y，-g），其中传感器的主距为g。

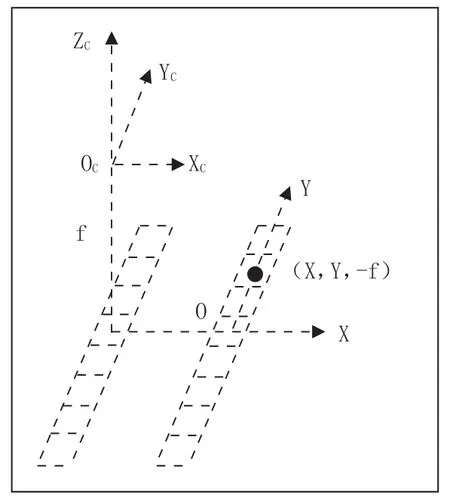
图3 传感器坐标系

1.4 本体坐标系

遥感卫星的坐标原点通常位于卫星的质心，坐标系为（OR-XRYRZR）如图4所谓为遥感卫星本体坐标系。其中，XR轴的方向即为卫星的飞行方向，YR轴即为遥感卫星的横轴，ZR根据右手法则进行分析确定。

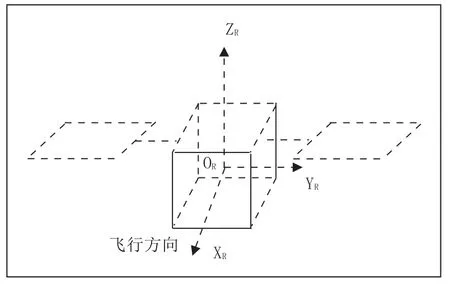
图4 本体坐标系

2 光学遥感卫星影像成像几何模型

2.1 严密几何成像模型

严密几何成像模型是根据影像的物理特性来进行计算的，通过遥感卫星影像像点坐标和对应物坐标来建立函数关系的。想要获取清晰的高分辨率影像，需要采用线阵CCD扫描的方式，该扫描方式会根据卫星的实际运行情况来成像，满足共线方程。其中，对共线方程的扩展需要进行以下考虑一下几点。

2.1.1 投影中心位置及线阵CCD姿态变化

在光学遥感卫星影像成像几何模型中，投影中心位置及线阵CCD姿态变化是影响基础共线方程扩展中外方位元素变化的主要因素。而投影中心位置的确定及线阵CCD姿态变化主要需要参考卫星的卫星的运动轨迹、地球自转等因素。其中卫星的运动轨迹为一固定轨迹，满足开普勒定律；地球自转在进行几何成像模型构建的短时间内基本可认定为绕地球自转轴开展的匀速运动；系统扰动则可通过转换进行时间函数表达[3]。

2.1.2 星载相机复杂的光学结构

星载相机与一般相机结构存在巨大差异。星载相机需要同时兼顾光学遥感卫星影像处理的高分辨率需求和宽视场成像。同时，由于卫星承载能力限制，有要求星载相机最小化的质量。因此，在有限的相机结构尺寸限制下，相机多采用折反式复杂光学成像结构或采用多镜头进行组合成像。这一光学结构极容易导致复杂的坐标转换问题。

2.2 通用数学成像模型

根据工艺发展、卫星需求等的不同，卫星平台与平台之间的机构通常存在一定的差异。随着光学遥感卫星中所使用的相机分辨率不断提升，传统的空间坐标对应关系发生了改变，需要针对卫星平台中不同功能、类型的传感器开发不同的处理数学成像模型。与严密几何成像模型相比，该种成像模型具有更明显的数学抽象和近似，并不像严密几何成像模型一样能够直接描述成像误差与影像变形间的关系。同时通用数学成像模型也并不需要像严密几何成像模型一样利用影像获取卫星对地定位结构信息。能在很大程度上取得一般成像模型无法获得的独立性，降低高分辨率卫星在进行相同类型作业时的图像处理复杂程度。但是，由于通用数学成像模型具有理论上的局限性，通常无法对影响变形大、覆盖范围大或地形起伏变化较大的情况进行图像处理。

2.3 抽象几何成像模型

抽象几何成像模型在实际应用中需要借助多种数据（卫星影像和对应的RPC参数），其中RPC参数只是一个求解或者优化数据和相关参数的工具，不具备任何物理意义，需要在RPC的基础上借助数学成像模型对影像中的数值进行处理，该方法在一定程度上影响了几何定位的精准度[4]。因此，在RPC参数的基础上，重新设置了一套适用于光学遥感卫星几何成像模型高精度对地定位技术要求的模型，即抽象几何成像模型，该模型具有非常重要的意义与实用价值。

3 星历姿态背景下的卫星影像立体定位研究

在星历姿态背景下可以将遥感卫星影像转化为卫星成像的外方元素。如图5所示为多片影像联合立体定位示意图，可以通过两张以上的像点进行同名像点结合，然后再来分析确定对应点的地面坐标。

图5 多片影像联合立体定位示意图

由以上可知，两张以上的影响立体定位计算如下：

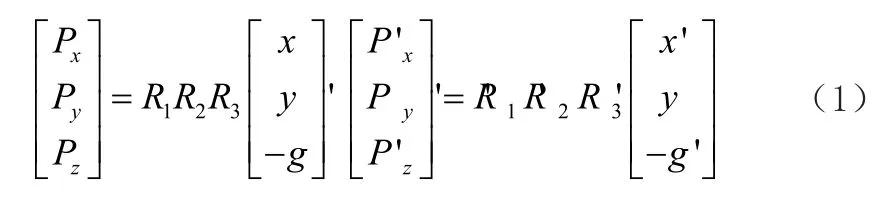
由公式（1）可得出：

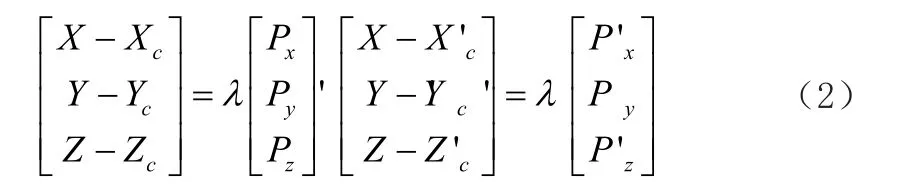
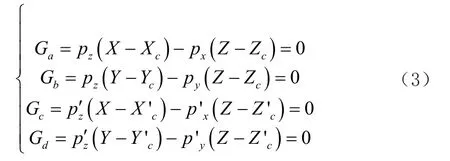
因此可以得出：

根据以上公式可求出多张影像的像点对应三维坐标，同理在公式（3）的基础上应用观测方程同样可以求出多片影像的立体定位[5]。

4 结语

我国在航空航天领域有了诸多重要的发展，现代卫星遥感技术已经成为国民经济与国防建设的重要标志。国产卫星影像几何定位精度虽然有了大幅提升，但仍与国外商业遥感卫星存在差距，在实际应用中有许多需求是无法满足的，因此，利用几何成像模型高精度对地定位技术进行研究是非常重要的，该技术可以扩大高分辨率遥感卫星影像应用。