模拟移动床色谱分离吴茱萸碱和吴茱萸次碱

2021-07-24姚传义郑震玮涂志贤卢英华

化工学报 2021年7期

姚传义，郑震玮，涂志贤，卢英华

（厦门大学化学化工学院，福建厦门361005）

引言

吴茱萸是芸香科植物吴茱萸、石虎、疏毛吴茱萸的干燥近成熟果实，为著名中草药，具有散寒止痛、降逆止呕、助阳止泻的功能[1]。吴茱萸碱和吴茱萸次碱是吴茱萸中的重要活性成分及质量控制指标，然而，现代医药研究揭示二者具有不同的药理功能。其中吴茱萸碱具有抗肿瘤[2-3]、抗老年痴呆[4]、减肥[5]、舒张血管及调节血压[6-7]等功能，而吴茱萸次碱则具有增强药物代谢酶活性[8]、治疗心血管疾病[9]及抗癌[10]的功效。因此，吴茱萸碱和吴茱萸次碱的分离纯化具有潜在的药物开发价值，对中药现代化有重要意义。

由于吴茱萸碱和吴茱萸次碱的结构相似（图1）、理化性质接近，很难利用常规分离方法如萃取、结晶等实现分离。张起辉等[11]利用硅胶柱色谱梯度洗脱从吴茱萸中分离得到5 个成分，鉴定为吴茱萸碱、去氢吴茱萸碱、吴茱萸内酯、对羟基苯甲酸乙酯及小檗碱，但硅胶色谱分离具有分离效率低、不可逆吸附、操作烦琐的缺点。Liu 等[12]利用高速逆流色谱，以正己烷/乙酸乙酯/甲醇/水=5/5/7/5（体积比）为溶剂体系分离了5种生物碱，包括吴茱萸碱、吴茱萸次碱、吴茱萸卡品碱（evocarpine）、1-甲基-2-[(6Z，9Z)]-6,9-十五二烯基-4-(1H)-喹诺酮和1-甲基-2-十二烷基-4-(1H)-喹诺酮，纯度均达到96%以上，但适宜溶剂系统的选择是一个挑战。

图1 吴茱萸碱和吴茱萸次碱的化学结构Fig.1 Chemical structures of evodiamine and rutaecarpine

模拟移动床（SMB）是一种连续制备色谱技术，由多根色谱柱首尾相连构成一个闭环系统，洗脱液进口、萃取液出口、进料口、萃余液出口将系统分为四个区带，通过进出口沿流动相方向的切换来模拟固定相的反向移动，避免了真实移动固定相的困难。SMB 因具有高效、高生产能力及连续操作的优点，已成功用于石油化工[13-14]、食品工业[15-16]、手性药物[17]及天然产物[18]的分离领域。近年来，人们又开发了很多SMB 过程的变体，如异步切换模型移动床或称Varicol 过程[19-23]、PowerFeed[24]和ModiCon[25]过程等，通过改变SMB 的操作模式进一步提升分离过程效能，其中，Varicol 过程通过异步切换，使得各区带柱子数目不局限于整数，从而实现了固定相的灵活分配，提高了产品的分离纯度或生产能力。本课题组建立了三区带Varicol 过程[26]，并用于香兰素与丁香醛的分离，在不增加设备投资的情况下，仅通过异步切换使生产能力较传统SMB 过程提高了40%以上[19]。

本研究拟采用模拟移动床技术分离吴茱萸碱和吴茱萸次碱，通过建模实现过程的优化设计，并利用异步切换策略提高生产能力。

1 数学模型

1.1 柱模型

对柱子取微元横截面进行质量衡算可得传质扩散模型：

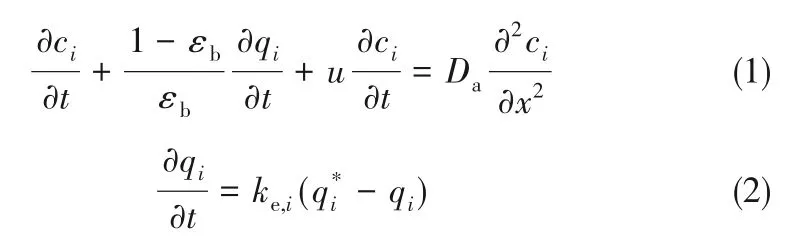
初始条件为：

边界条件为：

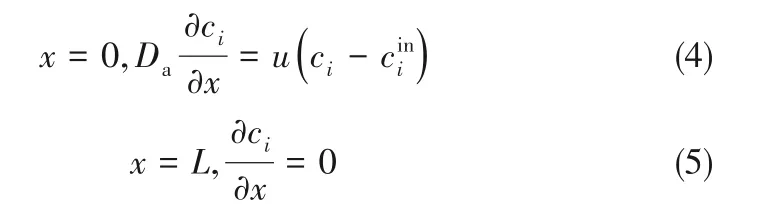
式中，L为柱子长度；cini为流入柱子的液相浓度，它与柱子所在位置有关。

对各进出口节点物料衡算可得：洗脱液进口节点

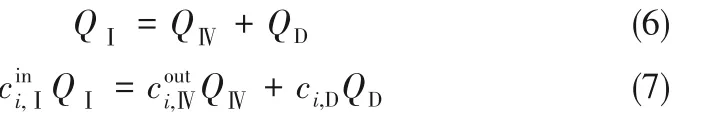
萃取液出口节点

进料口节点

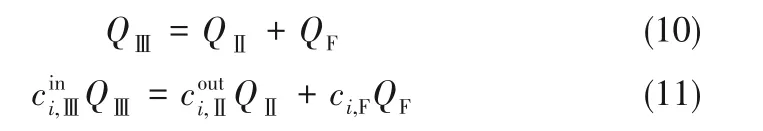
萃余液出口节点

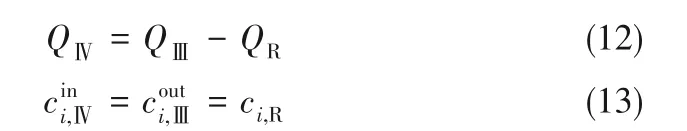
图2 Varicol过程实现平均构型[1,1.5,1.5,1]的异步切换策略Fig.2 Asynchronous switching strategy in Varicol for achieving the average configuration of [1,1.5,1.5,1]

式中，Q为流量；上角标in 表示进口，out表示出口；下角标Ⅰ、Ⅱ、Ⅲ、Ⅳ分别表示区带Ⅰ、区带Ⅱ、区带Ⅲ和区带Ⅳ；下角标D、E、F、R 分别表示洗脱液、萃取液、进料和萃余液。

1.2 异步切换过程

在传统SMB 过程中各进出口同时切换，因而各区带中柱子数目或称系统构型是固定不变的，而Varicol 技术中各进出口可以异步切换。图2 以5 柱四区带系统为例说明Varicol 操作过程，系统初始构型为[1,1,2,1]，在切换周期的中点即0.5ts时刻切换进料口F，此时构型变为[1,2,1,1]，在切换周期结束时切换洗脱液口D、萃取液口E 及萃余液口R，恢复初始构型。因而在一个切换周期内，前0.5 个周期构型为[1,1,2,1]，后0.5 个周期构型为[1,2,1,1]，则平均构型为[1,1.5,1.5,1]。Varicol 技术中各区带柱子数目不再局限于整数，有利于固定相在各个区带的合理分配，从而提高系统效能。

为描述Varicol过程，沿用文献[23]所做的定义。初始构型，即一个切换周期开始时各区带柱子数目：

平均构型，即一个切换周期各区带平均柱子数目：

各进出口的切换时间：

归一化切换时间，即各进出口切换时间除以切换周期ts：

由于每一个进出口在一个切换周期中都切换一次，因而归一化切换时间必然介于0～1之间：

各进出口的相对切换时间定义为:

由于在一个切换周期内，任意两个进出口的归一化切换时间之差必然介于-1～1之间，因此有：

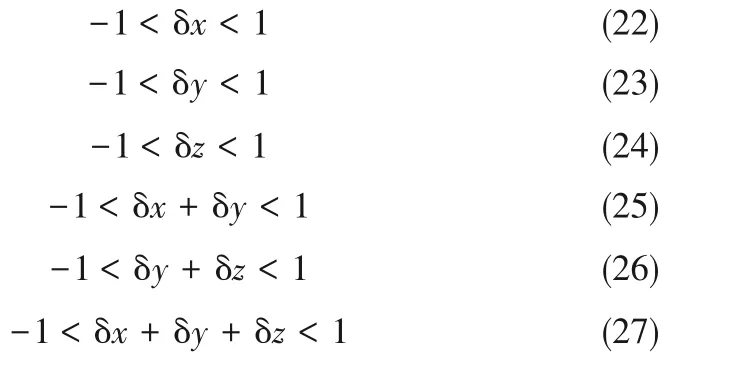
前文已经证实，对切换时间的平移不影响分离效果[23]。对归一化切换时间向量δt平移得到虚拟切换时间向量δt0：

可以发现δt0仅由3 个相对切换时间决定，但其分量值有可能为负数。要由δt0得到δt只需对其平移使各分量均为正值即可，按照习惯，通常令D口在切换周期的结束时刻进行切换，即令δt第一个分量δtD=1。

另外，利用相对切换时间很容易由初始构型得到平均构型[23]：

在对Varicol 优化过程中，可以利用相对切换时间δx、δy、δz作为决策变量，约束条件式（22）～式（27）构成一个十二面体[28]，其体积比式（22）～式（24）所限定的正立方体小了50%。利用优化得到的相对切换时间由式（29）～式（32）可得到平均构型，要得到切换策略，先构建δt0，然后通过平移得到δt。

下面以图2 所示Varicol 过程为例进行说明，由N0=[1,1,2,1]及Nˉ=[1,1.5,1.5,1]，由式（29）～式（32）易得δx=0，δy=-0.5，δz=0.5，构建δt0=[0, δx, δx+δy，δx+δy+δz]=[0, 0, -0.5, 0]，平移得到δt=δt0+1=[1, 1,0.5,1]，δt向量清晰指出洗脱液口D、萃取液口E、萃余液口R的切换时间为ts，而进料口F的切换时间为0.5ts。

对三区带Varicol 过程，由于不包含区带Ⅳ，即Nc,Ⅳ=Nˉc,Ⅳ=0，由式（32）可得δx+δy+δz=0，因而独立的相对切换时间只有两个，通常取δx和δy。

2 材料和方法

2.1 实验材料

吴茱萸碱(纯度99.9%)和吴茱萸次碱(纯度99.5%)购于成都瑞芬思生物科技有限公司，甲醇（HPLC 级）购于天津光复精细化工研究所，硫脲、乙酸铵、乙酸、异丙醇、辛烷均为分析纯，购于国药集团化学试剂有限公司。

C18 填料（粒径75µm）购于青岛海洋化工有限公司，采用干法装填于内径1 cm、长度15 cm 的不锈钢柱制备柱中。模拟移动床小试设备由作者实验室搭建，该系统包含3 台P230 Ⅱ泵（大连伊利特分析设备有限公司）及4 个EMTCSD8UW 高压选择阀（美国Valco 公司），单向阀用于避免流体的反向流动，萃取液口外接反压阀以方便流量的控制，萃余液口放空，其流量由系统压力自行控制，具体流程图请参考前文[19]。实验温度控制在30℃，所有实验均需等系统稳定（运行80个切换周期后），连续收集3个切换周期样品检测产品纯度。

样品分析采用大连伊利特P230 ⅡHPLC 系统进行，分析柱（4.6 mm×250 mm）固定相为10µm C18填料，分析流动相为甲醇/水=80/20(体积比)，流量为1 ml∙min-1，进样量20 µl，检测温度30℃，紫外检测波长254 nm。

2.2 孔隙率的测定

硫脲被广泛用作反相C18 色谱的不保留指示剂[29]。将硫脲溶于流动相中配制浓度为1 mg∙ml-1的溶液，在不同流动相流速条件下，测定其在制备柱上的保留时间t0，t0与总孔隙率εt的关系为：

式中，Vc=πd2L/4 为柱管内总体积，d为制备柱内径。

采用总孔堵塞法[30]测定外部孔隙率εb，其原理是先用疏水性溶剂堵塞固定相内孔，然后利用亲水性溶液测定不保留物质的保留时间。选用辛烷为疏水性溶剂，10 mmol∙L-1的乙酸铵水溶液（利用乙酸调pH到3.0）作为亲水性溶液。其操作步骤为：(1)利用异丙醇为流动相冲洗色谱柱120 min，流量为1 ml∙min-1；(2)以辛烷为流动相冲洗色谱柱120 min，流量为1 ml∙min-1；(3)拆下色谱柱，以二通连接管路，以5 ml∙min-1异丙醇冲洗管路5 min，再以2 ml∙min-1亲水性溶液冲洗管路5 min；(4)重新连接柱子，以1 ml∙min-1亲水性溶液冲洗色谱柱至稳定；(5)以1 mg∙ml-1硫脲溶于亲水性溶液为样品，在不同流速下测定其保留时间tb0。tb0与外部孔隙率εb的关系为：

根据总孔隙率和外部孔隙率，内部孔隙率可按式（35）计算：

2.3 吸附等温线测定

采用前沿分析法测定吸附等温线。将吴茱萸碱或吴茱萸次碱溶于流动相中配制不同浓度的溶液，每隔25 min，将进口溶液切换为更高一级浓度的样品溶液，流量恒定于3 ml∙min-1，记录多个浓度平台的穿透曲线。平衡浓度可由式（36）计算[30]：

式中，ck为第k级平台的进口浓度；t0,k为第k级平台的开始时间；tR,k为第k级平台的保留时间，取平台半高浓度的洗脱时间。

2.4 轴向扩散系数及有效传质系数的估算

轴向扩散系数利用Chung and Wen 关联式[31]计算：

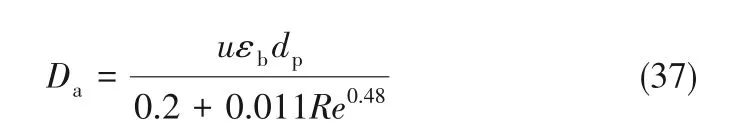
式中，dp为填料粒径，Re为Reynolds数。

有效传质系数按式(38)估算[32]：

式中，H为亨利系数；Dp为粒子内扩散系数；kf为膜传质系数。具体估算过程可参见文献[19]。

3 结果与讨论

3.1 总孔隙率及外部孔隙率

在不同流速下测定硫脲的停留时间，如图3 所示，t0与Vc/Q之间呈线性关系，通过线性回归可得总孔隙率εt=0.707。利用疏水溶剂辛烷进行孔堵塞后，再次测定不同流速下硫脲的保留时间，结果亦示于图3，通过线性回归得到外部孔隙率εb=0.353。根据式(35)可得内部孔隙率εp=0.547。

图3 C18制备柱上孔堵塞前后硫脲保留时间与Vc/Q之间的关系Fig.3 Relationship between retention time of thiourea and Vc/Q on the C18 preparative column before and after pore blocking

图4 前沿分析法测定吴茱萸碱和吴茱萸次碱的吸附等温线Fig.4 Adsorption isotherms of evodiamine and rutaecarpine by frontal analysis

3.2 吸附等温线

利用前沿分析法测定吴茱萸碱和吴茱萸次碱在30℃的吸附等温线三次，其中一次的实验结果如图4(a)所示。根据式(36)计算得平衡固相浓度，从图4(b)可知，两种物质的吸附等温线均可用线性关系描述，通过线性回归得吸附等温线方程：

需要强调一点，本研究中所使用溶质浓度较低（0.05 g∙L-1），这是由于吴茱萸碱和吴茱萸次碱在甲醇/水体系中的溶解度太低所致。

3.3 轴向扩散系数与有效传质系数

利用经验关联式(37)估算不同流速下的轴向扩散系数，如图5 所示，轴向扩散系数与流量Q之间呈线性关系，这是由于在实验条件范围内，Reynolds数很小，根据式(37)，Da与u呈正比也即与Q呈正比，经线性回归得到：

图5 不同流量下的轴向扩散系数与有效传质系数Fig.5 Axial diffusion coefficient and mass-transfer coefficients at different flow rates

利用式(38)估算吴茱萸碱和吴茱萸次碱在30℃的有效传质系数，结果如图5 所示，可以看到，两组分的有效传质系数随流量变化很小，这是因为流量主要影响外扩散即膜传质系数kf，而本研究所采用的固定相粒径较大，内扩散成为传质阻力的控制因素。为方便起见，取实验流量范围内的均值作为传质系数，得到ke,A=13.62 min-1，ke,B=21.73 min-1。

3.4 SMB操作

三角形理论被广泛用于SMB 过程操作条件的设计[33]，该理论中定义了第j区带的液固流速比mj:

对于二元线性体系，要实现有效分离，第Ⅱ、Ⅲ区带的流速比mⅡ与mⅢ均需要介于两组分的亨利系数HA与HB之间，因而在mⅡ-mⅢ平面上，两组分完全分离限定了一个三角形区域，即图6 中w、a、b 所围成的三角形区域。图中对角线上的操作点（包括a和b）生产能力为0（QF=0），不具有实际意义；w 点具有最大的生产能力，但由于它位于分离区域的边界上，操作并不稳定。因此，本研究中选择了5个操作点，即图6 中的P1～P5进行实验，这五个操作点与对角线的距离相同，即具有相等的进料流量。原料液浓度为cA=cB=0.05 g∙L-1，操作条件及实验结果如表1所示。

图6 mⅡ-mⅢ平面内的操作点Fig.6 Operation points in the mⅡ-mⅢplane

由表1 可看出，从P1到P5，随着QE增大，萃取液纯度下降，萃余液纯度上升，但萃余液纯度最高为96.1%，未能达到吴茱萸碱和吴茱萸次碱均大于99%的高纯度分离。这是因为三角形理论基于理想色谱条件，忽略了轴向扩散及传质阻力对柱效的影响，因而只适用于操作条件的粗略估计[19]。虽然可以降低操作点位置，使其与对角线距离更近，从而提高产品纯度，但进料流量也会随之下降。为了在保证产品纯度的要求下，尽量提高系统生产能力，采用基于数学模型的优化方法，设置第一区带流量固定在2 ml∙min-1，产品纯度大于99.5%，优化决策变量QE、QF和ts，优化目标为最大化进料流量，该优化问题可描述为：

在优化过程中，由优化算法产生决策变量即QE、QF和ts的值，通过求解模型方程式（1）～式（13）得到产品纯度PE和PR，并检验其是否满足纯度要求。优化算法采用复合形法[34]，该方法是单纯形算法在有约束优化问题中的扩展，即根据用户提供的初始点，构建2k个顶点的复合形（k为决策变量数目，对本问题为3），对最差点进行反射以获得一个新顶点，利用新顶点取代最差点以构成新的复合形，由此不断搜索以收敛到最优点。复合形法的优点是适用范围广，不需要对目标函数求导，缺点是收敛速度较慢[34]。

利用基于模型的优化得到SMB 过程最优操作条件如表2 所示，相对应的操作点位于图6 中P6位置。实验验证该操作点的纯度列于表1 中，吴茱萸碱和吴茱萸次碱的纯度均达到99%以上，实现了高纯度分离。与脉冲进样的间歇制备色谱[11]相比，SMB 分离过程连续进料，因而生产能力大幅提高；与高速逆流色谱[12]相比，SMB 利用了固定相的高选择性能力，可实现高纯度分离，且不需要使用复杂的溶剂系统。

表1 不同操作点的操作条件及产品纯度Table 1 Operation conditions and product purities at different operation points

表2 SMB及Varicol过程的最优操作条件Table 2 Optimum operation conditions for the SMB and Varicol processes

3.5 Varicol操作

由于Varicol 过程通过异步切换可实现固定相的灵活分配，从而提高系统效能[20]，因此，本研究尝试通过异步切换提高处理量。对于三区带过程，相对切换时间只有δx与δy两个独立变量[19]，同时，对于初始构型N0=[1, 1, 2]，为了确保在异步切换过程的任何时刻，三个区带均存在，需要Nˉc,j≥1（j=Ⅰ,Ⅱ,Ⅲ），相应地要求δx、δy和δx+δy介于-1～0 之间。因此，优化问题可描述为：

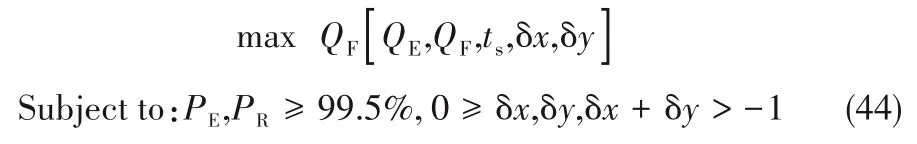
利用复合形法优化得到相对切换时间δx=δy=-0.16，其他条件列于表2。根据式（29）～式（31）可得平均构型为Nˉ=[Nc,Ⅰ-δx，Nc,Ⅱ-δy，Nc,Ⅲ+δx+δy]=[1.16，1.16，1.68]，该操作点对应于图6 中P7位置。根据相对切换时间，构建δt0=[0，δx，δx+δy]=[0，-0.16，-0.32]，通过平移δt0得到δt=δt0+1 =[1，0.84，0.68]，切换策略如图7所示。

通过求解数学模型，可得Varicol 过程中吴茱萸碱和吴茱萸次碱在各柱中浓度分布情况，切换周期中点时刻的浓度曲线如图8所示，为了对比，SMB 过程的浓度分布曲线亦示于图8。由图8可见，强保留物质吴茱萸次碱的浓度波主要位于区带Ⅱ，弱保留物质吴茱萸碱浓度波主要位于区带Ⅲ。由于Varicol 过程的进料流量增加，因而吴茱萸碱的浓度波平台高于SMB 过程，但吴茱萸次碱的浓度波平台高度相差不大，这是因为相比于SMB 过程，Varicol过程区带Ⅱ长度增加，而液相流量减小（参考表2），其结果是流动相在区带Ⅱ的停留时间增加，由于扩散及传质阻力的作用，使吴茱萸次碱浓度波变得更加扁平，降低了平台高度。由于Varicol 过程进料口在2.32 根柱子的位置，相比于SMB 过程右移了0.32根柱子的距离，因而从图8可以看出，Varicol过程两个物质的浓度波相比于SMB 过程右移，但吴茱萸碱的浓度波前沿是个例外，它在两个过程中基本重合，这是因为Varicol 过程中区带Ⅲ长度减小，为1.68根柱子，而SMB 过程区带Ⅲ有2根柱子，对三区带过程吴茱萸碱的浓度波最多迁移到R 口的位置（即4 柱出口位置），因而区带Ⅲ长度的减小导致吴茱萸碱浓度波变窄，即其浓度波前沿左移，而进料口的右移又驱使其浓度波前沿右移，两种因素共同作用使得Varicol 中吴茱萸碱的浓度波前沿与SMB过程处于非常接近的位置。显然，Varicol 中吴茱萸碱浓度波后沿的右移有利于提高萃取液口产品纯度，而吴茱萸次碱的浓度波前沿右移则可能降低萃余液口产品纯度，但实际上萃余液口仍然得到高纯度吴茱萸碱，这是由于Varicol 中区带Ⅲ长度的减小及流量的增加，使得液相在区带Ⅲ中停留时间减小，因而扩散及传质阻力对柱效的影响降低，从图8也可以看出，吴茱萸次碱的浓度波前沿比SMB 过程更为陡峭，因此，虽然Varicol 中吴茱萸次碱的浓度波前沿整体右移，但其末端位置却几乎与SMB 过程的吴茱萸次碱浓度波前沿末端处于相同位置，因而并未引起萃余液口产品纯度下降。

图7 实现平均构型[1.16,1.16,1.68]的切换策略Fig.7 Switching strategy for achieving the average configuration of[1.16,1.16,1.68]

图8 SMB及Varicol过程在切换周期中点时刻的柱内浓度分布曲线Fig.8 Concentration profiles of SMB and Varicol processes at the mid-point of switching period

对优化得到的Varicol 过程操作条件进行实验验证，结果列于表1，萃取液口及萃余液口纯度都达到99%以上，与标准SMB 过程相比，在产品纯度要求相同的前提下，进料流量即生产能力提高了12%。文献中[35-38]经常将Varicol 过程的异步切换策略作为离散变量来进行优化，即列出所有可能的构型组成构型空间，将切换周期四等分为四个亚区间，对每一个亚区间由优化算法从构型空间中选择一个构型来模拟其分离效果。这种方法的结果是每个区带的平均柱子数目均为1/4 的倍数，无法充分发挥Varicol 灵活分配固定相的优势，例如本文优化得到的平均构型[1.16,1.16,1.68]就无法利用这种方法获得。而本文方法将切换策略转换为连续变量即三个相对切换时间的优化，能更为精细地调控固定相在各区带中的分配，以充分发挥Varicol 过程的优势。

4 结论

利用三区带模拟移动床进行吴茱萸碱和吴茱萸次碱的高纯度分离，以C18 为固定相，甲醇/水=70/30（体积比）为流动相。通过前沿分析法测定了两种生物碱的吸附等温线，均符合线性吸附等温线，吴茱萸碱和吴茱萸次碱的亨利系数分别为3.11和5.25。基于数学模型对标准模拟移动床及Varicol过程操作条件进行了优化，并对优化操作条件进行了实验验证，采用4柱三区带模拟移动床，吴茱萸碱和吴茱萸次碱的纯度都达到了99%以上，Varicol 过程较标准SMB过程生产能力提高12%。

符号说明

c——液相浓度，mg∙ml-1

Da——轴向扩散系数，cm2∙min-1

dp——固定相粒径,cm

H——亨利系数

ke——有效传质系数，min-1

L——色谱柱长度，cm

Nc——柱子数目

Q——流量，ml∙min-1

q,q*——分别为固相浓度及与液相浓度平衡的固相浓度，mg∙ml-1

ts——切换周期，min

δt——归一化切换时间