露天煤矿内排土场台阶高度优化与稳定性研究
2021-07-24杨福卿张传伟王知乐才庆祥
杨福卿,田 涯,张传伟,王知乐,陆 翔,才庆祥
(1.昆明煤炭设计研究院,云南 昆明 650011;2.中国矿业大学 矿业工程学院,江苏 徐州 221116)
我国通过露天开采生产出的煤炭资源在整个能源架构中所占比例不断提高[1],其高效安全的生产方式有力地为诸多行业的发展提供支撑[2]。但同时,随着露天煤矿采场不断地推进、降深,其开采范围、深度也在不断提高,这一过程伴随着大量剥离物的产生[3],这些松散的表土与岩石通过运输至特定区域建设成为排土场,通过与采场之间的关系分为内排土场和外排土场,为不同粒径组成下的颗粒在人工堆积后固结形成的边坡[4]。排土场的稳定性一方面决定着企业生产过程中承担的安全风险,一方面限制着排土场的边坡角,即受单个排土台阶高度的限制。对于内排土场,单个排土台阶越高,可以有效地控制端帮稳定性[5]、提高采场有限空间的利用率来减少采场外土地占用、提供更多空间提高土地复垦面积、减小运输过程克服的高差以节省运输成本等,缺点会使边坡的安全稳定系数降低,存在地质灾害隐患。
针对排土场台阶高度,国内外学者进行了大量的研究。田华[6]建立了倾斜基底上排土场堆载形成的边坡几何结构、力学模型,揭示了排土场边坡稳定性随着高度的增长呈二次函数规律递减,采用模拟分析确定准东露天矿平直和凹形排土台阶的最大安全高度为64 m和80 m,内排跟进压帮之后首采区西帮靠帮开采的最佳角度为38°。艾啸韬等[7]借助元胞自动机用窄级配粗粒土模拟了高台阶排土场的粒径分级的不均匀与随机性,探讨了不同堆排方案下边坡的安全稳定性,结果表明排土场发生“拉-剪”破坏,土体中上部有圆弧形滑坡趋势,下部变形表现为沉降,顶部平台产生拉剪裂缝。翟文龙等[8]借助太沙基极限承载力理论与排土场设计规范等的极限堆高计算方法,得到排土场基底承载力和极限堆高,通过多种方法计算得到该排土场在严格控制好坡度和第1台阶高度的基础上可堆置的极限高度为205 m,为排土场的优化设计提供参考。蔡利平等[9]通过构建排土场表面积计算和排土容积计算的方法,分析排土场的几何参数与评价指标之间的关系,在保证边坡稳定性的情况下多次进行网格划分,得到了排土场优化设计的几何参数,结果表明采用多次划分的方式能够有效地获取排土场几何参数设计的最佳模型。综上所述,内排土场台阶高度的提高在矿山安全、经济与社会效益方面有着重要的意义。因此,在以往学者的研究基础上,在松散物料重构效应与离散元数值模拟理论的方法上,针对天池能源南露天煤矿内排土场所获取的物料展开研究。
1 排土场土石混合体力学特性试验
天池能源南露天煤矿内排土场单台阶的高度为30 m,台阶坡面角33°。南露天煤矿内排至2020年底,最大排弃高度为550 m水平,坑底为325 m水平,边坡角为15.232 2°,西帮排土场由8个30 m台阶和1个15 m台阶组成,南露天煤矿采场如图1。
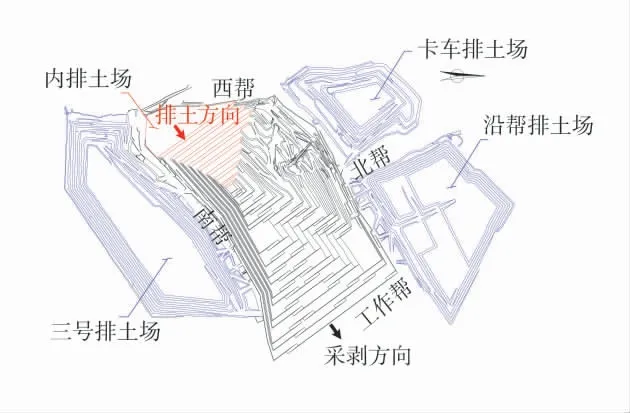
图1 南露天煤矿采场概况Fig.1 The general situation of south open pit coal mine stope
内排土场物料分别取自370 m水平与520 m水平,共取得试样46.99 kg(370 m水平22.41 kg,520 m水平24.58 kg)。将所取试样充分混合后通过粒径分级筛得到不同粒径范围的质量,西帮排土场所取物料粒径组成见表1。根据表中数据选取“土石阈值”为5 mm,根据JTG 3430—2020公路土工试验规程[10]中要求将试验所需最大颗粒粒径设为10 mm,以此对所取试验进行相似级配法的缩尺处理。
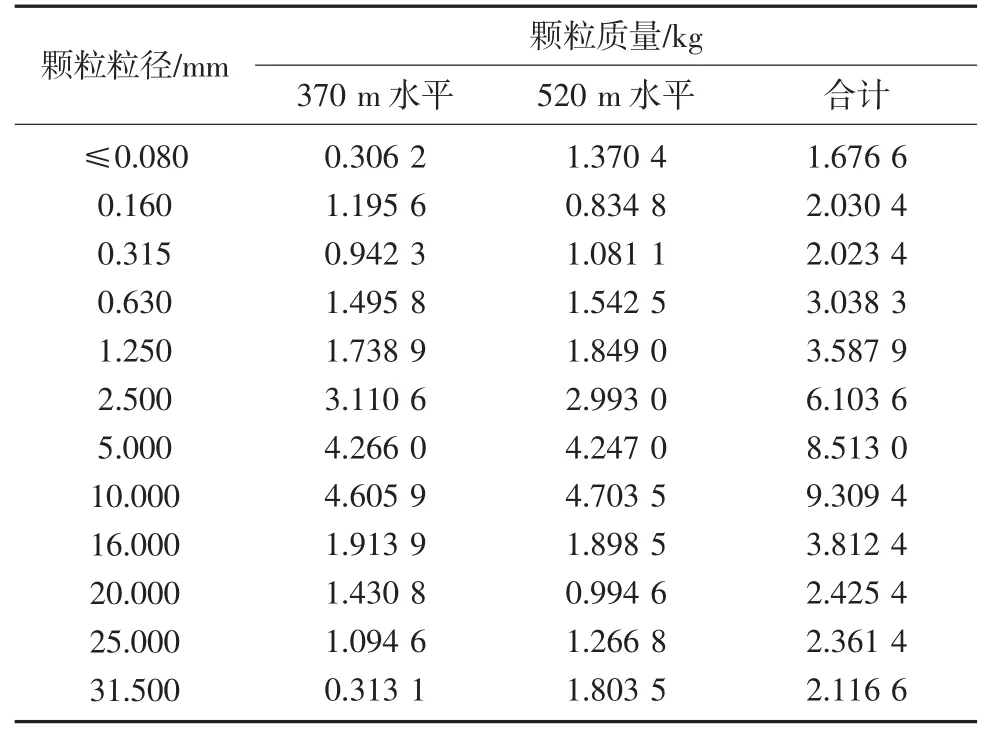
表1 西帮排土场所取物料粒径组成Table 1 The particle size composition of the material taken from the west dumping site
1.1 物料力学参数获取
宋仁忠等[11]在露天矿排土场稳定性分析中提出了排土场分层方法,该方法考虑物料在自重作用下的重构效应,较以往方法准确度较高。为此,沿用该方法对内排土场的物料进行分层,以往研究数据表明南露天煤矿排弃物料密度在1.98~2.21 g/cm3,为简化单杠杆固结试验设计,将排弃物料密度取为2.00 g/cm3,重力加速度取10 N/kg,计算得到物料所处不同位置的上覆载荷,以此分层。不同分层试样的上覆载荷见表2。

表2 不同分层试样的上覆载荷Table 2 Overburden loads of different stratified specimens
确定上覆载荷后进行单杠杆固结试验并脱模后进行无侧限抗压试验,单杠杆固结仪为南京土壤仪器厂WG-1型,无侧限抗压试验选用长春科新试验仪器有限公司的WDW-300型微控电子试验机。设定逐级加载的时间为6 h,每级加载76 kPa,在试样不再产生沉降后即可加载下一级载荷,并保证在最大载荷时加载重力的时间满足24 h。其中,固结试样的最大加载应力分为9种,与表2中相同,初始含水率为15%。
对脱模后的试样高度使用千分尺进行测量并称量试样质量,计算得到不同固结压力下的试样密度。不同固结压力下试样的密度如图2。由图2中可以得到,试样的密度和固结压力呈正相关,同时密度的离散程度也会有一定减小。
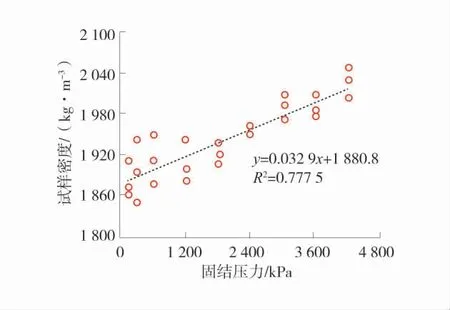
图2 不同固结压力下试样的密度Fig.2 The density of the specimen under different consolidation pressures
随后将试样切削成长度100 mm的标准试样进行无侧限抗压试验,以位移控制的方式进行加载,加载速度0.5 mm/min,结束方式为应变超过9.5%。不同固结条件下试样全应力-应变曲线如图3。由图3中可得,随着之前固结压力的增大,试样在无侧限抗压试验中表现出的弹性模量越大、峰值强度越高、残余强度越大。固结压力小时,试样内部胶结较差,容易生成剪切面,破坏后表现为残余强度;随着固结压力提高,试样出现应变软化现象。
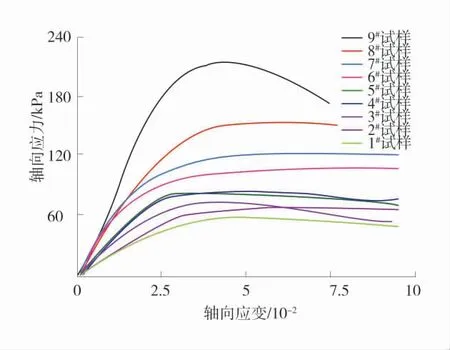
图3 不同固结条件下试样全应力-应变曲线Fig.3 Total stress-strain curves of samples under different consolidation conditions
1.2 离散元数值模拟参数标定
离散元模拟方法,由Cundall P A于1971年提出[12],可有力解决不连续介质的数值模拟。其中,颗粒流(PFC)离散元是将圆(球)形或不规则颗粒认为是介质的基本构成,通过颗粒间的细观胶结,最终使颗粒系统表现出宏观上的力学特性。程序的理论基础为:①牛顿第二定律;②力与位移关系。颗粒流离散元不要求位移连续,可以直接观察边坡从开始变形到破坏的整个过程(如坡体的滑移、倾倒、裂缝的发展),以及最终滑裂面的几何形状和位置。因此,颗粒流离散元是模拟边坡破坏问题较为理想的途径。
但在边坡计算之前需要在程序中先“还原”室内试验,通过调整细观的胶结参数使程序与室内试验中的应力-应变曲线相似,完成数值模拟的第1环节——参数标定。在参数标定时,首先在PFC中建立试样模型,因主要研究边坡,所用的颗粒数无法与真实一致,需要结合设备的计算能力进行颗粒数目调整。限制因素为西帮内排土场剖面计算时的颗粒数,同时需要注意,边坡模拟与室内试验模拟需要在同一尺度下进行[13]。因此,室内试验模拟将决定后期边坡稳定性模拟过程中的颗粒数n:

式中:n为小尺度试验中的颗粒数;Amin为室内试验模拟中试样面积,m2;Amax为边坡模型初始面积,m2;nmax为设备计算颗粒数目上限。
颗粒数目的下限受内尺度比限制[14]:

式中:Lmin为模型最小边界尺寸,m;Rmax为模型内颗粒最大半径,m。
通过式(1)与式(2),以及西帮内排土场的模型尺寸,可得到室内试验模拟中的颗粒数为2 225,试样高60 m,宽30 m。最小颗粒粒径为0.40 m,最大为0.64 m,随后将粒径超过0.52 m的颗粒替换为不规则的刚性簇。模型用于模拟胶结较差的土石混合体,故选线性接触黏结模型。在试错法进行多次计算后,得到细观参数与全应力-应变曲线。不同固结压力下土石混合体细观参数见表3,数值模拟中不同试样全应力应变曲线如图4。

图4 数值模拟中不同试样全应力应变曲线Fig.4 The total stress-strain curves of different specimens in the numerical simulation
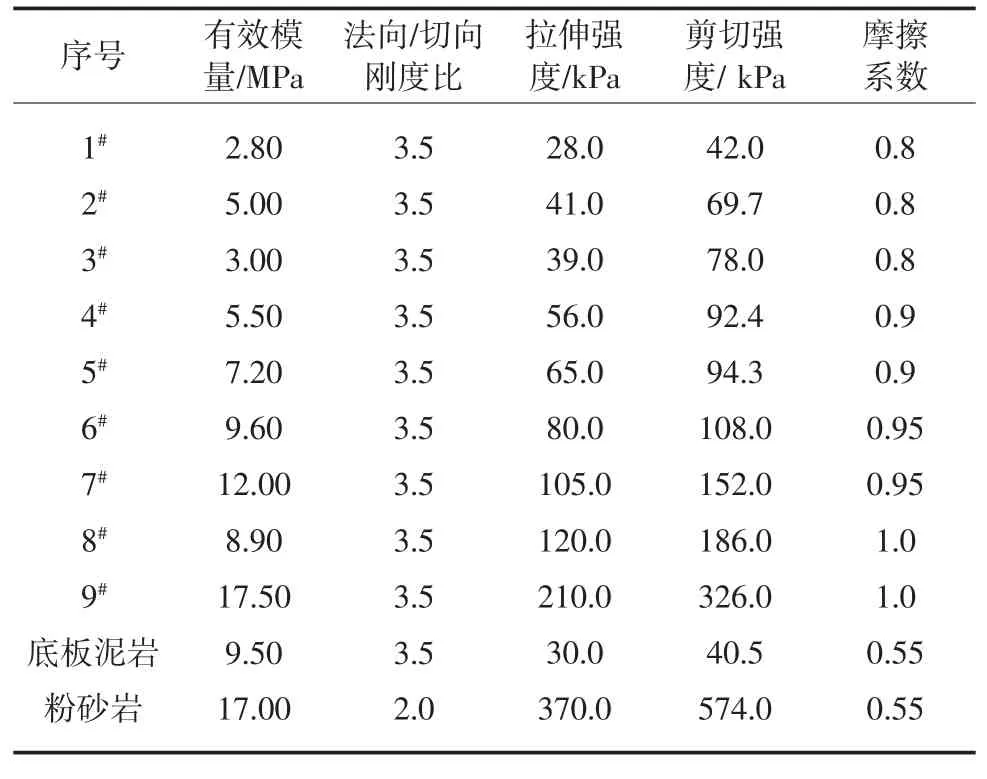
表3 不同固结压力下土石混合体细观参数Table 3 Meso-parameters of soil-rock mixture under different consolidation pressures
2 高段排土单层台阶最大高度
为优化南露天煤矿西帮内排土场台阶高度H,列出H为75、60、45、30 m这4种不同高度台阶,根据台阶所处位置将其分为“最下部排土场台阶”与“普通排土场台阶”。其中最下部排土场台阶建立在底板泥岩上,普通排土场台阶建立在内排物料上。模型中,最下部排土场台阶的坡脚距右侧约束边界的距离为100 m,即露天煤矿坑底安全距离;坡顶距左侧约束边界的距离为75 m,即内排土场平盘宽度。普通排土场台阶坡顶、坡脚距左、右侧约束边界均为75 m,不同高度的边坡模型如图5。
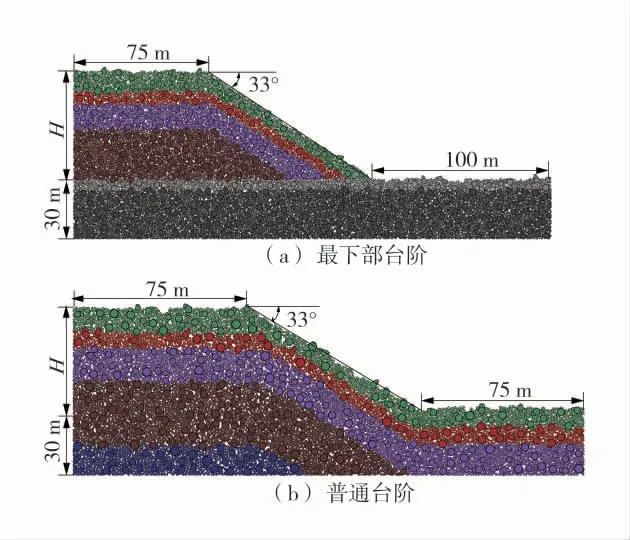
图5 不同高度的边坡模型Fig.5 Slope models of different heights
模型采用强度折减法对不同高度的边坡安全稳定系数获取,在颗粒流边坡模型中,影响边坡稳定性的参数为颗粒间细观的拉伸强度Tensile、抗剪强度Shear与摩擦系数fric,这3种细观参数对应着宏观中的黏聚力C与内摩擦角φ。在强度折减法原理的指导下对颗粒间的黏结强度和摩擦系数同时进行折减,直到边坡达到临界破坏状态,此时的折减系数即为边坡的安全稳定系数Fs,表示为:

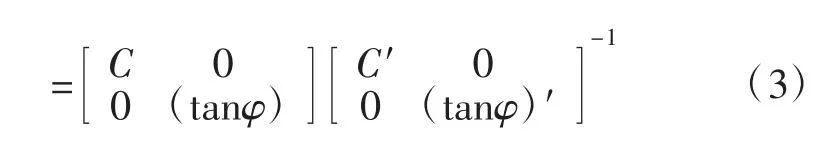
式中:Tensile′为临界破坏状态时的拉伸强度,Pa;Shear′为临界破坏状态时的剪切强度,Pa;fric′为临界破坏状态时的摩擦系数;C′为临界破坏状态时的黏聚力,Pa;φ′为临界破坏状态时的内摩擦角,(°);E为单位矩阵。
其中强度折减法的失稳判据为限制计算步内平均不平衡力比是否满足收敛要求,同时对边坡坡面处颗粒的平均速度进行计算。折减系数在限定范围内采用二分法取值,精度为0.001。
以最下部排土场45 m台阶为例,在折减系数为1.448时,边坡失稳,出现了典型的圆弧形滑坡,折减系数为1.448时边坡不同时步位移变化如图6。

图6 折减系数为1.448时边坡不同时步位移变化Fig.6 The slope displacement changes in different simultaneous steps(F s=1.448)
从图6可以得到,模型在计算到10 000步时,滑体后缘颗粒出现了少量(0.20~0.32 m)的位移,滑体前缘位移相比后缘较小,滑动初期表现为坡顶处的不均匀沉降;计算至15 000~50 000步时,滑体与滑床位移的区分度较大,圆弧形滑动面清晰,滑体累积位移量在此期间不断增大;模型从50 000步直到计算结束(平均不平衡力比小于1×10-5)的过程中,滑体沿圆弧形滑动面产生位移的同时伴随坡顶颗粒向坡脚滚落。计算结束时,滑体表面颗粒位移较大(12.51~39.42 m),颗粒越靠近滑动面位移越小(0.32~5.01 m)。
计算过程中坡面区域的平均速度曲线如图7(折减系数1.448),平均速度对应的坡面位移云图如图8(折减系数1.448)。
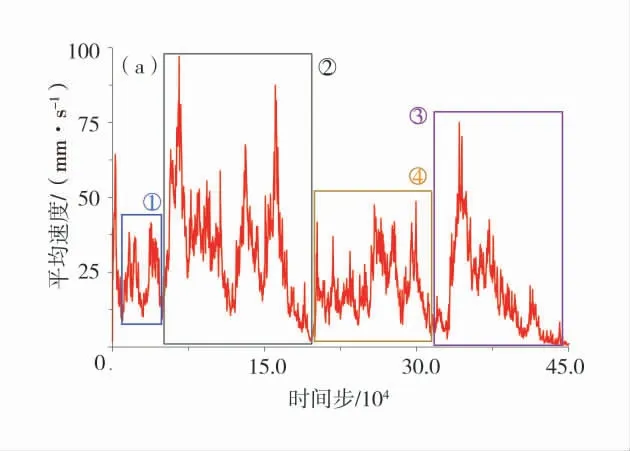
图7 坡面区域的平均速度曲线(折减系数1.448)Fig.7 Average velocity curves of slope area

图8 平均速度对应的坡面位移云图(折减系数1.448)Fig.8 Cloud images of slope displacement corresponding to average velocity(F s=1.448)
根据不同时步下的位移云图与平均速度的曲线可将边坡滑坡到稳定的历程分为4部分:①第1部分(0~50 000步):对应位移云图①,边坡开始出现圆弧形滑坡趋势,滑体前缘从坡脚剪出,坡面颗粒平均速度最大为38.7 mm/s,速度曲线波动较小;②第2部分(50 000~200 000步):对应位移云图②,此时边坡的颗粒滚落并堆积在原坡面中部区域,坡面处的颗粒位移不断增大,速度曲线出现多次波动;③第3部分(200 000~325 000):对应位移云图③,此时坡面的颗粒在达到收敛标准后重新开始滑动,从这部分中的速度曲线来看,边坡第二次达到稳定状态;④第4部分(325 000~450 000):对应位移云图④,平均速度曲线中得到边坡出现第4次滑动,该阶段结束后边坡稳定,此后速度曲线再未出现较大波动。
不同折减系数(1.437、1.444、1.447、1.448)下监测区域的平均速度曲线如图9。
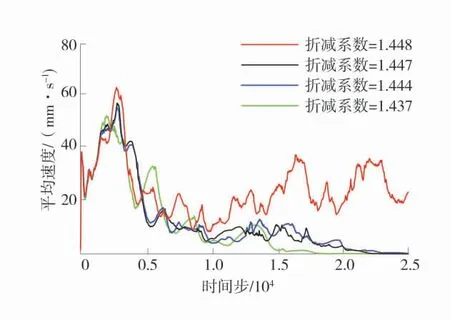
图9 不同折减系数下监测区域平均速度变化Fig.9 Variation of average velocity in monitoring area under different F s coefficients
由图9可知,折减系数为1.437、1.444、1.447时平均速度曲线能够从参数变化后的短暂波动回归稳定,表现出模型固有的自稳性。在折减系数为1.448时平均速度不断波动,出现速度突变,与其他3组折减系数下的平均速度曲线差异较大。由此可得,内排土场最下部45 m台阶的安全稳定系数为1.447,此时为极限平衡状态,当折减系数为1.448时边坡失稳。
通过以上的方法,对剩余7种排土场边坡的稳定性进行了计算,不同高度下边坡安全稳定系数如图10。台阶高度在30~60 m之间时,边坡安全稳定系数变化较小,但当台阶高度超过60 m之后,边坡安全稳定系数变化较大。不同区域的排土场边坡都在高度达到75 m时,安全稳定系数小于1.0,边坡无法在此高度下保持稳定状态。同时,最下部排土场安全稳定系数均大于普通排土场台阶,差值在0.198~0.294之间。
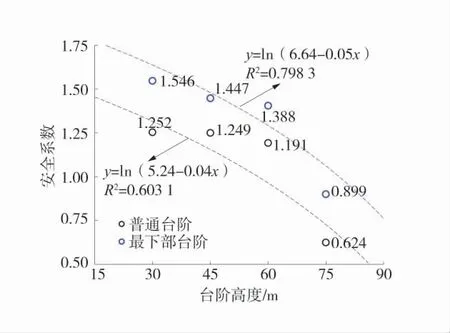
图10 不同高度下边坡安全稳定系数Fig.10 Safety factor of slope at different heights
3 结论
1)试样密度会随着固结压力的增大,并在无侧限抗压试验中表现出弹性模量增大、峰值强度提高、残余强度提高的现象。在固结压力小时,试样内部胶结较差,容易生成剪切面,破坏后表现为残余强度,随着固结压力提高,试样表现出应变软化现象。
2)边坡在计算过程中,滑体后缘颗粒会先出现少量位移,表现为坡顶处不均匀沉降,随后滑体与滑床位移的区分度较大,圆弧形滑动面形成且清晰,最后滑体沿圆弧形滑动面滑动的同时伴随坡顶颗粒不断向坡脚滚落。滑体表面颗粒位移较大,颗粒靠近滑动面位移逐渐变小。
3)边坡模型在小于等于安全稳定系数的折减系数时,平均速度曲线会在短暂波动后回归稳定,在大于安全稳定系数的折减系数时,平均速度曲线不断波动,出现速度突变。
4)台阶高度在30~60 m之间时,边坡安全稳定系数变化较小,当高度超过60 m后,边坡安全稳定系数变化较大,呈对数函数变化。同时,最下部排土台阶稳定性均优于普通排土台阶。但不同区域的排土场边坡都在台阶高度达到75 m时,都无法保持稳定状态。
