矩形巷道全长锚固锚杆力学模型分析及设计
2021-07-24谷拴成杨超凡
谷拴成,王 盼,杨超凡
(西安科技大学 建筑与土木工程学院,陕西 西安 710054)
煤炭作为我国的主要能源支柱,对国家经济起着举足轻重的作用[1]。在煤炭开采中,如何快速安全实现巷道支护显得尤为重要。由于锚喷支护施工速度快、支护效果好、造价经济,因此被广泛应用[2]。巷道锚喷支护设计方法的丰富与改进经历了漫长的研究过程,因早期理论研究的滞后,使得巷道锚喷支护设计普遍使用工程类比法。随着原位测试技术与计算机技术的发展,理论计算法、现场监测、非线性大变形力学设计法及数值模拟等多种方法开始应用于巷道支护设计中[3-9]。现阶段,对于圆形巷道围岩变形及锚杆支护的研究已有较为成熟的理论[10-15],因此在矩形巷道支护设计中,常将矩形巷道等效为圆形或椭圆形巷道来研究围岩变形及应力分布规律,从而对巷道锚杆进行分析设计。廖保明等[16]基于弹塑性力学理论,采用等效椭圆法,确定了矩形巷道锚杆(索)支护参数。冉金林等[17]基于围岩松动圈理论,运用等效圆法和压力拱法计算得出巷道顶板松动圈范围,并对锚杆、锚索参数进行设计。宋涛[18]以柠条塔煤矿S1201工作面回采煤巷为依托,基于等效椭圆的巷道设计方法对回采巷道进行支护设计研究。以上研究促进了锚杆支护设计的发展,但也存在少许不足,即圆形巷道围岩变形规律与矩形巷道不同,并不能准确反映矩形巷道锚杆受力情况,使支护设计产生误差。为此,根据柠条塔煤矿S12001运输巷道的现场监测得到巷道顶板围岩变形规律,建立矩形巷道顶板梁模型,考虑煤岩体抗压强度大于抗拉强度的特点,根据弹塑性理论,研究巷道顶板在上覆煤岩体自重应力场作用下的挠曲变形。基于顶板梁变形特点,进一步运用中性点理论对矩形巷道全长锚杆支护机理进行分析,并提出其锚杆支护设计方法。
1 巷道顶板围岩变形监测
柠条塔煤矿S12001运输巷道埋深200 m,巷道断面尺寸宽6 m高4 m,煤层平均厚度为4.3 m,基本顶一般厚度为12.9 m,成分以细粒砂岩为主。直接顶一般厚度为9.55 m,成分以细粒砂岩为主。底板一般厚度为8.75 m,成分以碳质泥岩为主,岩层物理力学参数见表1。
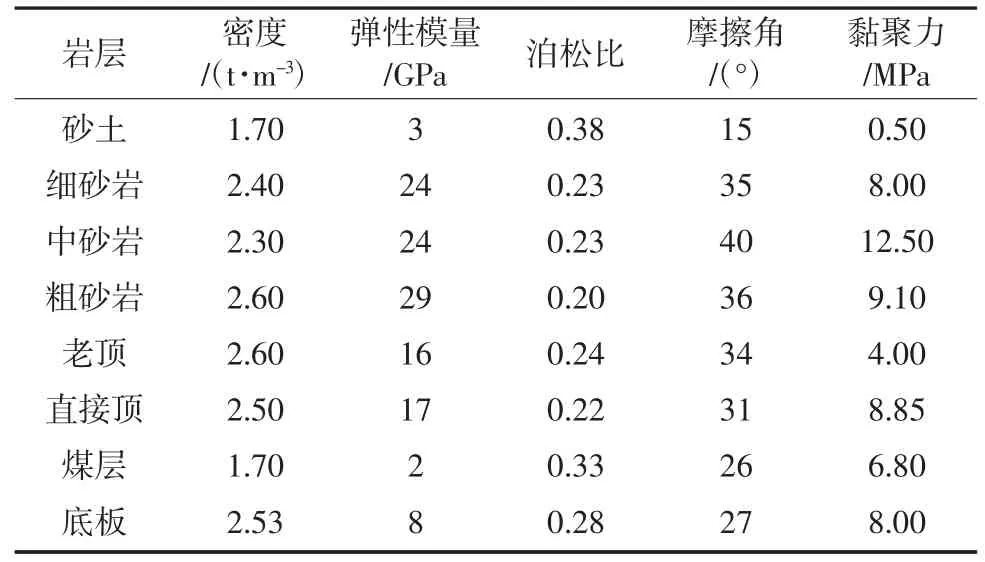
表1 煤岩体物理力学参数Table 1 Physical and mechanical parameters of coal and rock mass
测站布置在柠条塔煤矿S12001工作面运输巷道。顶板离层仪监测点安装位置分别距顶板表面跨中部位0.5、1.0、1.5、2.0、2.5、3.0、4.0、5.0、6.0 m。收敛计测点安装位置为距巷道左帮部0.5、1.5、2.5、3.0、3.5、4.5、5.5 m的顶板表面处,实测离层曲线及顶板表面下沉量如图1。

图1 实测顶板下沉量Fig.1 Actual roof subsidence
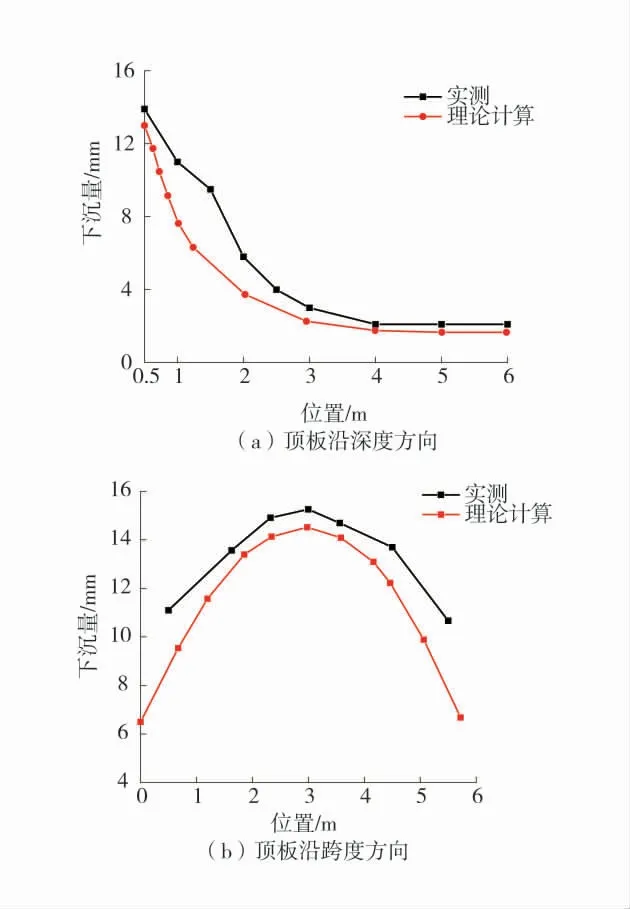
巷道变形稳定后,顶板跨中部位沿深度方向不同位置的下沉变形以及沿跨度方向不同位置处的下沉变形绘制为曲线如图2。由图2可知,巷道顶板表面的沉降值最大,向岩体内部逐渐减小;顶板表面不同位置处,沉降值并不相等,顶板跨中部位沉降值最大,向两帮逐渐递减。

图2 实测巷道顶板下沉变形曲线Fig.2 Measured roadway roof subsidence deformation
2 矩形巷道顶板梁模型建立及分析
2.1 顶板梁模型建立
将巷道顶板简化为简支梁,梁的横截面近似简化为矩形。顶板梁材料视为理想弹塑性材料,按平面应变问题进行分析,建立的顶板梁模型如图3。图中,2l为顶板梁计算长度,m;2h为变梁高度,m;b为梁宽,m;q为梁承担的上覆岩土体自重荷载,kN/m。

图3 顶板梁模型Fig.3 Mechanical model of roof beam
2.2 顶板梁弹塑性状态分析
为了求得顶板梁在弹性和塑性状态下的挠曲方程,首先对顶板梁截面的弹性和塑性演化阶段进行分析,求得不同阶段梁截面所对应的弯矩。继而根据平截面假定得到顶板梁在弹性和塑性状态下的挠曲方程。
顶板梁截面上应力分布随着煤岩体材料进入塑性阶段的不同呈现不同情况,顶板梁截面弹塑性阶段演化图如图4。图中,σt为顶板围岩的极限抗拉强度,MPa;σc为顶板围岩的极限压强度,MPa;β为顶板围岩抗拉屈服强度与抗压屈服强度的比值;e为中性轴的偏移离距离,m;y为顶板梁上层弹塑性区交界处距梁中性轴的距离,m;βy为下层弹塑性区交界处距梁中性轴的距离,m。

图4 顶板梁截面弹塑性阶段演化图Fig.4 Elastoplastic phase evolution of roof beam section
当顶板梁截面受拉侧最大拉应力小于顶板围岩的极限抗拉强度时,整个截面处于弹性状态,其截面上的正应力分布如图4(a);当顶板梁截面受拉侧最大拉应力达到顶板围岩的极限抗拉强度时,顶板梁截面受拉侧应变将继续增大,应力值不再增加,截面受拉侧塑性区逐渐扩大,此时为保证梁截面上正应力之和为0,中性轴开始偏离,如图4(b);当顶板梁截面受压侧最大压应力达到顶板围岩的极限压强度时,该侧也将进入塑性状态,如图4(c)。
2.2.1 顶板梁弹性状态分析
当顶板梁截面的最大正应力等于围岩的极限抗拉强度时,处于弹性极限状态下的顶板梁高为[19]:

式中:σmax为梁截面所受的最大正应力,MPa;y′为计算点到中性轴的距离,m;I为惯性矩,m4;Me为弹性极限状态下顶板梁跨中弯矩,N·m;he为弹性极限状态下的顶板梁高,m。
由式(1)、式(2)解得:
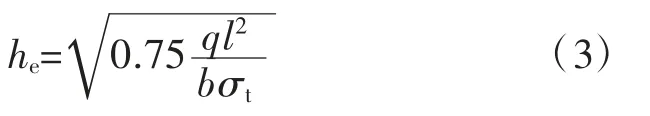
弹性状态下顶板梁跨中挠度为:

式中:ωe为弹性状态下顶板梁跨中挠度,m;E为围岩的弹性模量,MPa。
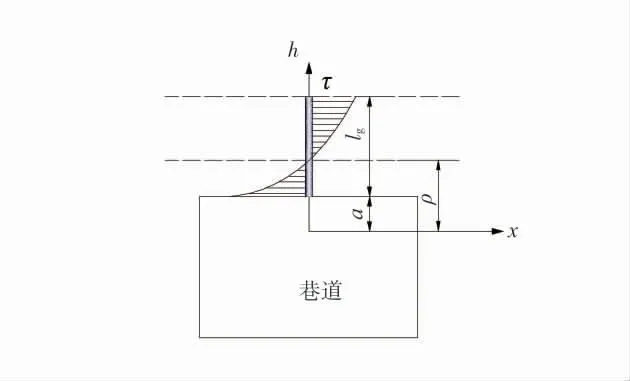
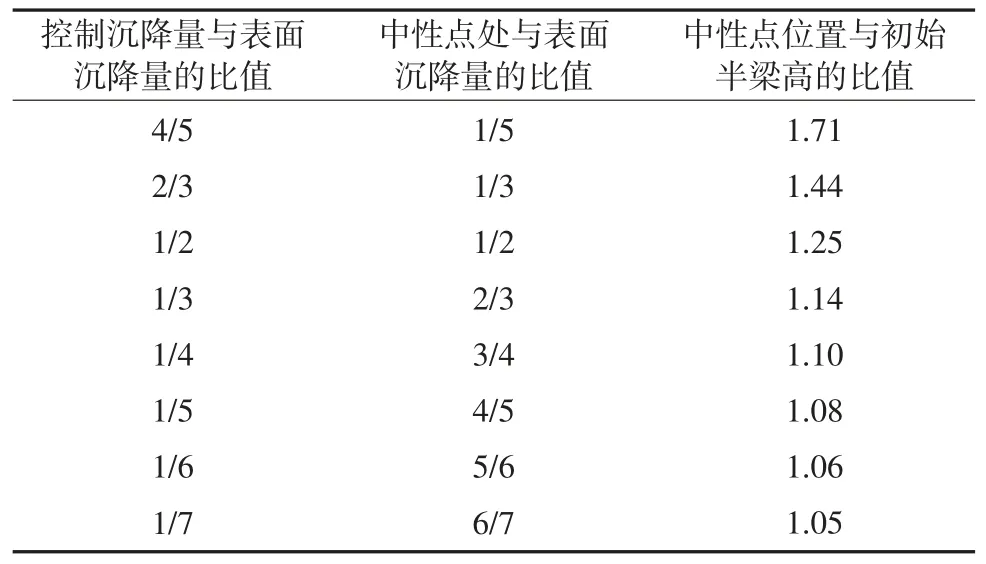
由式(3)可知,当h≥he时,顶板梁处于弹性状态;当h 2.2.2 顶板梁弹塑性状态分析 当梁截面处于弹塑性第2阶段状态时,离心距及截面弯矩为: 式中:M为梁截面弯矩,N·m。 当y=0时,即截面处于完全塑性状态,如图4(d),此时截面处于塑性状态下的弯矩为: 式中:Mp为梁截面处于完全塑性状态下的弯矩,N·m。 应用平截面假定可得顶板梁塑性状态下挠曲方程,分别如式(8)、式(9)(取β=1/6)。 式中:ω为顶板梁挠度,m。 根据式(8)、式(9)可知顶板梁的挠度在不同位置处是不同的,在顶板梁跨中位置x=l处挠度最大,由跨中向两边递减,与监测所得顶板围岩沿跨度方向变形规律一致。 当x=l时,代入式(9)可得巷道顶板跨中部位梁截面处于塑性状态的挠度为: 式中:ωp为顶板跨中部位梁截面处于塑性状态下的挠度,m。 根据式(7)可得顶板跨中部位梁截面处于塑性状态下的最大弯矩为: 式中:Mmax为顶板跨中部位梁截面处于塑性状态下的最大弯矩,N·m。 当顶板梁截面上的最大正应力等于围岩极限抗压强度时,可求得塑性状态下的顶板梁高为: 式中:hp为塑性状态下的顶板梁高度,m。 根据以上分析可知,当h≤hp,顶板梁处于塑性状态,此时顶板梁跨中挠度方程为式(10)。 当h≥he时,顶板梁处于弹性状态,此时顶板梁跨中挠度方程为式(4)。 当he 式中:ωep为顶板梁处于弹塑性状态时顶板梁跨中挠度,m。 当h不同时,可得到处于不同状态不同深度处顶板围岩的变形值。顶板围岩变形沿深度方向随h的增大逐渐减小,顶板围岩表面处变形最大,向岩体内部逐渐减小,在趋于无限远处(h→∞)为0,与现场监测所得顶板围岩沿深度方向的变形规律一致。 根据现场监测结果以及理论推导可知,巷道顶板跨中部位的下沉值最大,因此以顶板跨中部位作为关键点,在此基础上运用中性点理论[20]对全长锚固锚杆支护机理进行分析,并提出锚杆支护设计方法。 在全长锚固锚杆靠近巷道一端,顶板围岩向巷道内变形,锚杆阻止围岩变形而受到向下的剪应力;在锚杆远离巷道端,围岩要阻止锚杆向下位移而使锚杆受到向上的剪应力,故在锚杆上必有1个中性点,此处的剪应力为0,中性点位置如图5。图中a为初始半梁高,m;ρ为中性点位置,m;lg为锚杆的长度,m;τ为锚杆所受的剪应力,MPa。 图5 中性点位置Fig.5 The position of neutral point 根据锚杆全长上剪应力之和为0可得[20]: 剪应力τ的分布规律取决于顶板围岩变形,锚杆各点上剪应力的大小应与该点锚杆对岩体的相对位移成正比[20],即: 式中:K为顶板岩体的剪切刚度,kN/m2;△u为锚杆对顶板岩体的相对位移,m。 在锚杆中性点处,锚杆的位移与围岩的位移相等,因此,锚杆相对于围岩的位移就是各点岩体的位移与中性点位移之差,再减去锚杆相对于中性点的伸长量,由于锚杆的伸长量较小,可忽略不计[21],故: 式中:uρ为中性点位移,m;u为顶板围岩下沉量,m。 根据式(14)~式(16)得: 式中:B为参数,顶板梁处于弹性状态下时,B=0.31ql4/bE,顶板梁处于弹塑性状态下时,B=((4.64he3-0.31hp3)ql4)/((he3-hp3)bE),顶板梁处于塑性状态下时,B=4.64ql4/bE。 解得,中性点位置为: 将不同的锚杆长度与初始半梁高的比值(lg+a)代入式(18)可得到相应的中性点位置与初始半梁高的比值(ρ/a),锚杆长度与中性点位置的关系见表2。 表2 锚杆长度与中性点位置的关系Table 2 Relation between bolt length and the position of neutral point 矩形巷道顶板围岩控制沉降量与中性点处围岩沉降量及顶板表面围岩沉降量之间的关系为: 式中:uk为矩形巷道顶板围岩控制沉降量,m;ua为顶板表面围岩沉降量,m。 可将式(19)变换为: 根据式(10)得: 将以上关系整理可得控制变形量与中性点的关系(表3)。 根据表3中控制沉降量与表面沉降量的比值uk/ua可得中性点位置与初始半梁高的比值ρ/a,然后查表2便可求得锚杆长度lg。 表3 控制变形量与中性点的关系Table 3 Relationship between the control deformation quantity and the neutral point 在求得锚杆中性点位置后,进一步对锚杆应力分布进行分析。 由式(15)、式(16)可得锚杆剪应力: 由式(22)可知,锚杆最大剪应力发生在孔口h=a处,在设计时,最大值不得超过锚杆的锚固强度。 在锚杆中取一微段,对锚杆轴向应力进行分析。可得锚杆微段静力平衡微分方程为: 式中:σh为锚杆微段轴向应力,MPa;dh为锚杆微段长度,m;d为锚杆直径,m。 根据式(18)、式(22)、式(23)可得: 式中:C为积分常数。 根据边界条件,当h=a时,σh=0可得: 在已知锚杆允许抗拉强度[σ]、刚度系数k、巷道宽度2l、锚杆长度lg、岩土体密度ρy及岩土体弹性模量E的条件下,可根据式(25)可求得锚杆直径d。 为了验证本文推导理论的合理性,下面结合柠条塔煤矿S12001运输巷道进行全长锚固锚杆支护设计及参数分析。 已知围岩刚度系数K=3.2×102MPa,锚杆允许抗拉强度[σ]=200 MPa,锚杆锚固强度[τ]=3 MPa,取半梁初始高度a=1.4 m。 根据uk/ua=0.94/1.4,由表3得ρ/a=1.45,由表2可知lg=1.2×a=1.68 m,取lg=1.7 m。根据式(25)得锚杆直径为:d=17 mm,取d=18 mm。 将现场监测巷道顶板下沉变形与理论计算结果比较,顶板沿跨度及深度方向不同位置处下沉变形对比如图6,可知,现场监测巷道顶板下沉变形与理论计算结果基本一致,验证了理论的可靠性。 图6 顶板沿跨度及深度方向不同位置处下沉变形对比Fig.6 Comparison of roof subsidence deformation at different positions along the span direction and depth direction 根据式(22)、式(25)可将锚杆所受的剪应力和轴向应力绘制为曲线,锚杆剪应力分布图如图7,锚杆轴向应力分布图如图8。 图7 锚杆剪应力分布图Fig.7 Shear stress distribution of bolt 锚杆上剪应力以中性点为界,两端剪应力方向相反,锚杆最大剪应力发生在孔口。锚杆最大轴向拉应力发生在中性点处,锚杆两端轴向应力为0。锚杆剪应力最大值为2.84 MPa<[τ]=3 MPa;锚杆轴向拉应力最大值为186.06 MPa<[σ]=200 MPa,锚杆所受剪应力与最大轴向应力均符合设计要求。 1)根据现场监测得到的巷道顶板围岩变形规律,建立了顶板梁模型。考虑煤岩体抗压强度大于抗拉强度的特点,根据弹塑性理论,推导出巷道顶板在上覆煤岩体自重应力场作用下的挠曲变形计算式。巷道顶板围岩表面跨中部位处竖向位移最大,并向岩体内部以及巷道两帮逐渐减小。 2)以顶板围岩变形最大处,即顶板跨中部位作为关键点,依据中性点理论,对矩形巷道全长锚固锚杆受力进行分析,并提出了支护设计方法。锚杆上剪应力以中性点为界,两端剪应力方向相反,最大剪应力发生在孔口;锚杆轴向拉应力在中性点处最大,两端为0。在设计时,孔口处锚杆剪应力不得超过锚杆锚固强度;锚杆的最大轴向应力不应超过锚杆材料允许的抗拉强度。 3)结合实际工程对巷道顶板进行支护设计,同时将理论计算的顶板围岩下沉变形值与现场监测结果进行对比,结果表明,根据理论设计的锚杆受到的剪应力与轴向应力均符合要求;理论计算的顶板围岩下沉变形量与现场监测结果接近,从而验证了模型的可靠性。
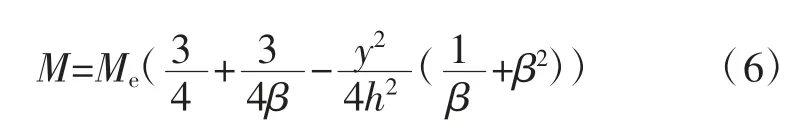
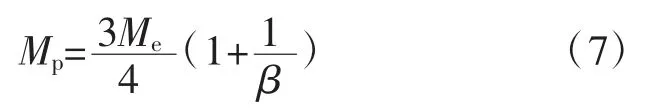





3 不考虑预张力条件下全长锚杆受力分析及设计
3.1 锚杆中性点位置计算



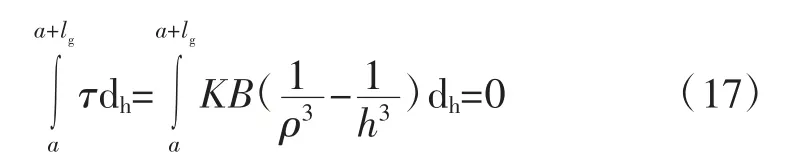





3.2 锚杆应力分析
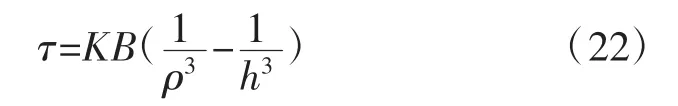
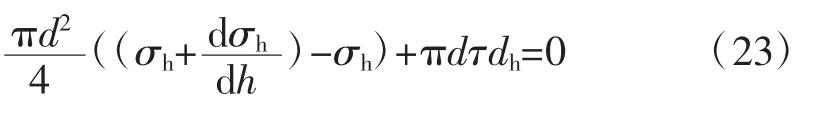

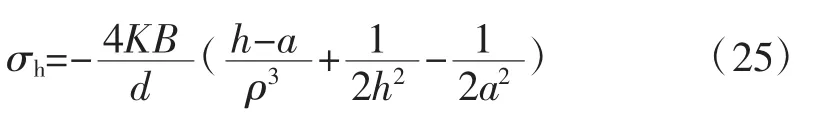
4 工程应用
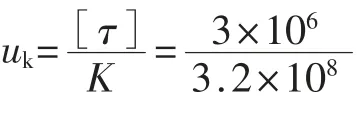

5 结 语
