张拉整体结构模块组合的力密度法找形与分析
2021-07-23程丽宋健张赵威程钦锟潘友胜
程丽 宋健 张赵威 程钦锟 潘友胜


摘 要:首先在用力密度法对张拉整体单元找形的基础上,对模块化组合的张拉整体结构进行找形分析;其次以三杆张拉整体单元及双模块结构为算例,用Matlab工具软件编程绘出结构的形态,同时阐述这种组合结构的形态特性;最后验证了这种找形可以推广到任意N模块,对实际工程应用具有重要意义。
关键词:张拉整体结构单元;找形;力密度法;模块化组合
0 引言
“张拉整体”这一概念最初由美国学者Fuller提出[1],由此概念,张拉整体结构被各国学者广泛研究,并且将张拉整体结构(Tensegrity Structures)定义为:一种处于自平衡状态的特殊索杆结构[2],索杆的组合使结构处于连续张拉状态并保持稳定。张拉整体结构最早广泛应用于雕塑作品中[3],近几十年逐渐成为国内外热门话题,学者们将这种结构与拓扑结构联系起来,从而把张拉整体思想逐渐应用到实际工程中,涉及航空航天、建筑、生物、智能机器人等多个领域。
张拉整体结构的形状具有多样性,找形是为了使其几何形式满足自应力准则[4],确定其几何构型及其预应力,来形成一种自平衡且稳定的体系,它是张拉整体结构设计中的关键。张拉整体结构找形中常见的算法有力密度法、数值方法[5]、改进鱼群算法[6]、粒子群算法[7]、遗传算法[8]等,其中力密度法是一个被广泛认可的重要找形方法。
通过连接组合张拉整体单元形成的模块化张拉整体结构是建立模块化张拉整体结构的主要方法。Snelson在1968年建立了通过沿着轴线连接的张拉整体结构[9];Fuller提出了最初的线型张拉整体结构并构造出了理想状态的线型张拉整体[10],所以这种线型的连接是模块化组合的最普遍方法。
本文以张拉整体单元为研究对象,用数值方法求出節点坐标,通过力密度法找到结构的平衡构型,以三杆张拉整体结构单元为算例,先对三杆张拉整体结构找形,再引入重叠率方程对找形后的单元模型进行模块化组合。利用工具软件Matlab编程绘出组合后的图形,并对最终形成的模块化结构的特性进行分析。
1 张拉整体单元找形
力密度法最早由Linkwitz和Schek于1971年提出[11],由Vassart和Motro[12]于1999年首次用于张拉整体结构的找形分析;利用力密度法找形时需要设定的基本参数有结构的拓扑构型(即求连接矩阵)、边界约束条件、平衡状态内力等,计算结构的力密度和各个杆件的力密度值,从而确定结构构型中的预应力。
1.1 建立结构的拓扑构型
张紧结构预应力的稳定性取决于连通性,这里用连接矩阵表示其结构构型。
张拉整体结构中一个成员l的两端节点由a指向b,在a-b节点的连通性矩阵Cl可定义如下:
Cl(a,b)= 1, l的连接起点a,-1,l的连接终点b, 0, 无连接关系 (1)
基于公式(1),节点间的连接关系用连接矩阵表示为:
1.2 以节点坐标建立平衡矩阵
结构中每个节点处的平衡方程由力密度和连接到节点的绳索表示,节点和连接节点之间的节点的坐标差与力密度有关,力密度与外部载荷处于平衡状态,结构处于平衡状态时,可以表示为:
Aq=f(3)
式中:A为结构系统中杆的平衡矩阵;q为杆的力密度向量;f为作用在节点上的外部载荷。
可以构造出如下形式平衡矩阵:
A=CTdiag(Cx)CTdiag(Cy)CTdiag(Cz)(4)
1.3 力密度
力密度矩阵表示为:
D=CTdiag(q)C(5)
力密度矩阵D中元素按式(6)可以求出:
D(a,b)= -qab, 如果a≠l,∑l=a qal, 如果a=l,求和 0, a与l不相连,(6)
1.4 平衡矩阵奇异值分解
将平衡矩阵奇异值分解:
A=M∑NT(7)
其中Mk=[m1 m2 … mk]是平衡矩阵A分解成的一个左奇异向量,Ns=[n1 n2 … ns]是平衡矩阵A分解成的一个右奇异向量,diag(*)和∑为对角矩阵。
1.5 数值算例
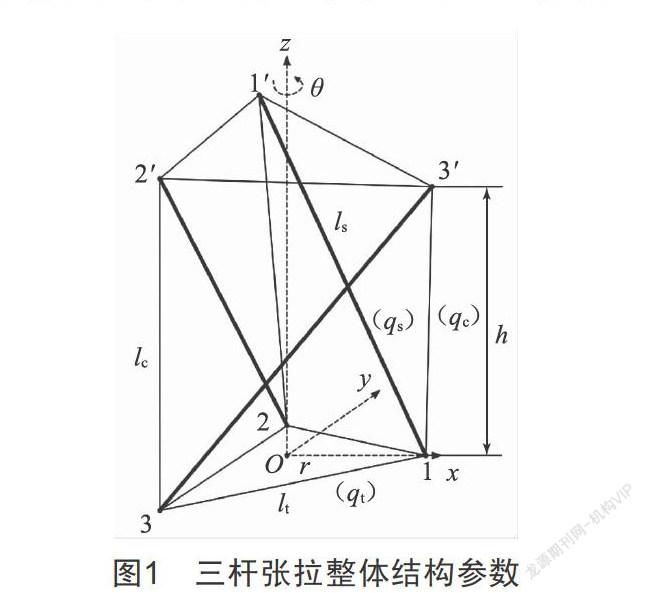
以图1的三杆张拉整体结构为例:在结构的底面三角形建立笛卡儿坐标系,其中上下端面扭转角度θ、杆长ls、水平索长lt为已知条件,利用公式(8)(9)(10)求上下端面外接圆半径r、高度h及最小竖索长lc,求出节点坐标向量x、y、z。
h2=ls 2-(2r2-2r2cos θ)(9)
lc 2=h2+2r2-2r2cos(-θ)(10)
建立连接矩阵:
C=1 -1 0 0 0 00 1 -1 0 0 01 0 -1 0 0 00 0 0 1 -1 00 0 0 0 1 -10 0 0 1 0 -11 0 0 0 0 -10 1 0 -1 0 00 0 1 0 -1 01 0 0 -1 0 00 1 0 0 -1 00 0 1 0 0 -1(11)