基于粒子群优化（PSO）超限学习机预测新疆参考作物蒸散量

尹起 周建平 许燕 李志磊 樊湘鹏 魏禹同

摘要： 參考作物蒸散量（ET0）的准确预测对于作物需水量预测、农田精准灌溉和提高水资源利用效率等具有重要意义。为了解决传统方法获取ET0的弊端，本研究基于粒子群优化（Particle swarm optimization，PSO）-超限学习机（Extreme learning machine，ELM）预测ET0。通过选取新疆地区3个站点（乌鲁木齐、喀什、哈密）的最高气温（Tmax）、最低气温（Tmin）、平均相对湿度（RH）、风速（u2）、光照时间（n）等气象数据，建立PSO-ELM预测模型，对模型精度和普适性进行研究，并通过与ELM、Makkink、I-A模型的对比，探究不同气象因子组合模型的预测精度。结果表明，PSO-ELM模型在5种气象因子输入下具有最高预测精度（平均R2=0.974 7，平均MAE=0.252 0 mm/d，平均RMSE=0.364 3 mm/d）。由PSO-ELM6模型与ELM、Makkink、I-A模型的对比结果看出，在相同的气象因子输入条件下，3个站点用PSO-ELM6模型预测的效果最好。通过对PSO-ELM3模型在新疆地区普适性的研究发现，该模型具有较高的预测精度（平均R2=0.946 5，平均MAE=0.307 0 mm/d，平均RMSE=0.356 9 mm/d）。不同站点、不同气象因子输入的PSO-ELM模型能够较为精准地反映气象因子与ET0之间复杂的非线性关系，且模型在新疆地区的普适性较好，可以为新疆地区逐日ET0预测提供新的方法。

关键词： 新疆;粒子群优化;超限学习机;参考作物蒸散量;模型精度

中图分类号： S27;TP312 文献标识码： A 文章编号： 1000-4440（2021）03-0622-10

Prediction of reference crop evapotranspiration in Xinjiang based on particle swarm optimization（PSO） optimized extreme learning machine

YIN Qi1， ZHOU Jian-ping1， XU Yan1， LI Zhi-lei2， FAN Xiang-peng1， WEI Yu-tong1

（1.College of Mechanical Engineering，Xinjiang University，Urumqi 830000，China;2.Engineering Training Center，Xinjiang University，Urumqi 830000，China）

Abstract： Accurate prediction of reference crop evapotranspiration （ET0） is of great significance in predicting crop water demand， precise irrigation of farmland and improving water resource utilization efficiency. To solve the disadvantages of traditional methods in obtaining ET0， ET0 was predicted based on particle swarm optimization （PSO）-extreme learning machine （ELM） in this study. By selecting meteorological data such as maximum temperature （Tmax）， minimum temperature （Tmin）， average relative humidity （RH）， wind speed （u2） and illumination time （n） of three stations in Xinjiang （Urumqi， Kashgar and Hami）， the PSO-ELM prediction model was established. The accuracy and universality of the model was studied， and the prediction accuracy of models combined with different meteorological factors was explored by comparing with ELM， Makkink and I-A models. The results showed that， PSO-ELM model showed the highest prediction accuracy under the input condition of five meteorological factors （average R2=0.974 7， average mean absolute error=0.252 0 mm/d， average root mean square error=0.364 3 mm/d）. The prediction effect of PSO-ELM6 model was the best under the same meteorological factor input conditions of three stations by comparing the PSO-ELM6 model with ELM， Makkink， I-A models. The research on the universality of PSO-ELM3 model in Xinjiang showed that， the model had high prediction accuracy （average R2=0.946 5， average mean absolute error=0.307 0 mm/d， average root mean square error=0.356 9 mm/d）. The PSO-ELM model with different meteorological inputs at different stations can accurately reflect the complex non-linear relationship between meteorological factors and ET0， and the model shows good generalizability in Xinjiang， which can provide new methods for daily ET0 prediction in Xinjiang.

Key words： Xinjiang;particle swarm optimization;extreme learning machine;reference crop evapotranspiration;model accuracy

参考作物蒸散量（ET0）是水循环研究中的重要组成部分，也是优化农业用水的重要变量，在水资源可持续管理及农业精准灌溉中起着重要作用[1]。在农业生态系统中，约2/3的降水量由作物蒸散过程损失[2-3]。由于频繁的干旱及农业、个人和工业用户之间对水资源的竞争，目前的农业生产用水量已经减少[4]。因此，有必要为灌溉管理者和水利研究人员提供一个准确的工具来估算参考作物蒸散量。ET0的获取方法较多，通常可以使用蒸渗仪或涡流协方差系统直接测量，但是使用、建设和维护蒸渗仪的成本较高。因此，使用基于气象因子经验和半经验建立的数学模型是一种更加符合实际且不需要额外代价的方法，如Hargreaves-Samani模型、Priestley-Taylor模型、Makkink模型等，但是这些数学模型受到多种因素影响，很难准确预测ET0[5]。联合国粮食及农业组织（FAO）推荐FAO-56 Penman-Monteith（PM）方法用于计算ET0的标准值，该方法需要大量气象数据（相对湿度、最高气温、最低气温、太阳辐射和风速等），但是这些数据并不总能从气象站获取，在大多数发展中国家，这些气象数据往往是缺失或无法获取的[6]。

近年来，机器学习模型被应用于各个领域的科学和工程研究中以处理各种问题，如建模、优化和预测等[7-12]。使用机器学习模型通过选择输入（添加或删除输入因子），并找到变量（输入和目标变量）之间隐藏的复杂关系。此外，机器学习在ET0的预测方面也得到了大量应用[13-20]，且气温是被证明与ET0相关性最好的因子[21-22]。本研究选择基于最高气温（Tmax）、最低气温（Tmin）的多种气象因子组合模型对试验结果进行分析。

张皓杰等[23-24]采用超限学习机（Extreme learning machine，ELM）对中国不同地区的ET0进行建模预测，研究在不同气象因子输入下模型的拟合程度，并且得到了较好的结果。虽然ELM算法已经被许多研究者在不同的工程领域中得到验证，但是该算法的参数（随机初始化的输入权重和隐藏阈值）会限制模型的准确程度。在此背景下，本研究提出1种粒子群优化-超限学习机（PSO-ELM）预测ET0的方法，并将该算法与传统ELM算法及2种经验模型进行比较，分析在不同地区输入不同组合气象因子的最佳预测模型，并通过对模型的普适性分析，筛选出新疆不同地区逐日ET0的最佳计算方法，以期为ET0的高精度预测提供一定的参考。

1 材料与方法

1.1 研究区域和数据集划分

新疆维吾尔自治区位于中国西北地区，地处亚欧大陆腹地，属于温带大陆性气候。考虑到新疆不同地区地理区域的差异性，选取站点需要有代表性，本研究选取的3个主要研究站点为新疆地区6个气象站点中的乌鲁木齐牧试站（地理位置为87°11′E、43°27′N，海拔为1 930 m）、喀什站（地理位置为75°45′E、39°29′N，海拔为1 385 m）、哈密站（地理位置为93°31′E、42°49′N，海拔为737 m）。选取的用于模型普适性分析的辅助站点分别为阿勒泰站（地理位置为88°05′E、47°44′N，海拔为735 m）、昭苏站（地理位置为81°30′E、43°14′N，海拔为1 851 m）、和田站（地理位置为79°56′E、37°08′N，海拔为1 375 m）。本研究站点的地理位置见图1。本研究获取的平均气温（Tmean）、最高气温（Tmax）、最低气温（Tmin）、相对湿度（RH）、风速（u）、日照时长（n）等逐日气象数据来源于中国气象数据网（http：//data.cma.cn）。本研究站点的气象数据涵盖2009年1月至2019年12月的11年（132个月），站点气象资料完整且经过人工审核。本研究中的数据集采用留出法进行划分，以2009年1月至2017年12月的数据作为训练集，占总数据量的82%，以2018年1月至2019年12月的数据作为测试集，占总数据量的18%。取3次试验结果的平均值作为最终数据评价指标。

1.2 参考作物蒸散量计算方法

以联合国粮食及农业组织推荐的FAO-56 Penman-Monteith（PM）方法作为ET0计算方法获取标准ET0值，计算公式如下：

ET0=0.408△（Rn-G）+γ900T+273u2（es-ea）△+γ（1+0.34u2）（1）

式中，ET0为参考作物蒸散量，mm/d;T为平均气温，℃;△为气温-饱和水汽压关系曲线上气温为T时的斜率，kPa/℃;Rn为净辐射量，MJ/（m2·d）;G为土壤热通量，MJ/（m2·d）;γ为湿度计常数，kPa/℃;u2为2 m高度处的风速，m/s;es为饱和水汽压，kPa;ea为实际水汽压，kPa。上述每个变量的计算方法详见FAO-56[25]。

另外选取2种经验模型：

Makkink经验模型：

ET0=0.61△△+γRs2.45-0.12（2）

式中，Rs为太阳总辐射，MJ/（m2·d）;其余变量的含义与公式（1）相同。

Irmark-Allen（I-A）经验模型：

ET0=0.489+0.289Rn+0.023Tmean  （3）

式中，Tmean为当日平均气温，℃;其余变量的含义与公式（1）相同。

1.3 超限学习机

ELM是新加坡南洋理工大学黄广斌教授于2006年正式提出的[26]，旨在克服传统機器学习算法存在的大量人为调整参数、计算速度缓慢、泛化性能较差等问题。该算法是一种单隐含层前馈传播的神经网络，其输入层和隐含层之间的连接权重、隐含层神经元的阈值是随机生成的，设定完成后就不再调整。隐含层和输出层的权重不需要迭代调整，而是通过解广义逆求得，因此该算法在计算时间上有较大优势。ELM包括3层：输入层、隐含层和输出层。

对于输入N个不同的样本（xi，yi），xi=[xi1，xi2，…，xin]T∈Rn，ti=[ti1，ti2，…，tik]T∈Rk，设隐含层节点数为L个，激活函数为G（x），则该算法的表达式为：

ti=f（xi）=∑Lj=1βjG（wj·xi+bj），wj∈Rn， βj∈Rk（4）

式中，i=1，2，…，N;j=1，2，…，L;wj=[wi1，wi2，…，win]表示连接输入层到第j个隐含层节点的输入权重;βj=[βj1，βj2，…，βjk]T表示连接第j个隐含层节点到输出节点的输出权重;激活函数G（x）可选择Sigmoid函数、Sin函数等;wj·xi为向量wj和xi的内积;bj为隐含层第j个神经元的阈值。

将该表达式转为矩阵，可得：

Hβ=T（5）

由于H在训练前是已经确定的矩阵，该网络的训练转化为求输出权重的最小二乘解的问题，输出权重可表示为下式：

β=H+T（6）

式中，H+为隐含层输出矩阵H的Moore-Penrose广义逆[26]。

1.4 粒子群优化-超限学习机算法

由于ELM连接的输入层与隐含层的权重（w）和隐藏神经元阈值（b）是随机生成的，从而可能使模型进入局部最优，导致预测结果精度较差。粒子群优化算法是1种应用广泛的优化算法，是由Eberhart和Kennedy从生物群体的协作行为出发提出的，多用于调整机器学习模型参数，其在农业方面的应用也被证明是有前景的[27-28]。因此本研究利用PSO算法优化ELM的输入权重和隐含神经元的阈值。PSO中的每个粒子被认为是群中的一个个体，粒子的好坏用适应度函数的值判断，并通过个体和全局每步的最优位置不断更新，最终获得最优解。

在1个D维空间中，设含有n个粒子群X=（X1，X2，…，Xn），粒子i的位置（Xi）=（Xi1，Xi2，…，XiD）T，速度（Vi）=（Vi1，Vi2，…，ViD）T，粒子i和整个群的最佳位置分别为Pi=（Pi1，Pi1，...，PiD）T和Pg=（Pg1，Pg2，...，PgD）T，在粒子群迭代优化过程中，粒子i的位置和速度的更新表示为：

Xk+1id=Xkid+Vk+1id（7）

Vk+1id=ωvkid+c1r1（Pkid-Xkid）+c2r2（Pkgd-Xkid） （8）

式中，d=1，2，…，D;i=1，2，…，n;w为惯性权重，其值代表偏重于全局搜索和局部搜索的能力;k为当前迭代次数;c1、c2为学习因子;r1、r2为0～1中的随机数。

PSO-ELM算法的具体步骤如下：

（1）对数据集进行归一化处理，并划分训练集和测试集。

（2）设置ELM输入层、隐含层、输出层维度，设置PSO种群大小、最小误差、迭代速度、迭代次数、惯性权重、学习因子。

（3）计算粒子的适应度，选择均方误差（Mean squared error，MSE）作为适应度函数SMSE，表达式如下：

SMSE=1N∑Ni=1（Ti-Yi）2（9）

式中：N为总样本数;Ti为样本的实际值;Yi为样本的预测值。

根据上式计算个体的适应度，迭代优化个体和全局最优粒子的位置和速度;当迭代到达设置的最小误差或一定的迭代次数时终止，得到输入权重和隐含层阈值的最优参数;将最优参数带入ELM进行计算，输出最优解。

PSO-ELM算法的流程见图2。

1.5 算法参数设置

设算法模型输入气象因子的数量为m个，PSO-ELM算法和ELM算法的参数设置见表1。

1.6 模型评价指标

为了评价预测结果，选择决定系数（R2）、平均绝对误差（MAE）、均方根误差（RMSE）、整体评价指标（GPI）作为预测结果的评价指标，相关公式如下：

MAE=1MMi=1|yi-i|（11）

RMSE=1MMi=1（yi-i）2（12）

GPIj=3k=1αk（Zjk-Zk）（13）

式中，yi为真实值;i为预测值;yi—为真实值的平均值;M为预测模型的天数;GPIj为模型j的GPI值;Zjk为模型j参数k的值;Zk为模型参数k的中位数，当k=R2时，αk=1，当k=RMSE或MAE时，αk=-1;GPI越大，预测结果的准确度越高。

2 结果与分析

2.1 不同输入因子下PSO-ELM模型的预测精度分析

本研究是基于气温因子（Tmax、Tmin）进行分析的。由表2可知，包含气温因子且表现较差的模型在乌鲁木齐、喀什、哈密地区分别为PSO-ELM8、PSO-ELM4、PSO-ELM8，但模型的各项评价指标均优于不包含气象因子的模型（PSO-ELM9～PSO-ELM12），在这3个地区含有气象因子且表现最差的模型（喀什地区的PSO-ELM4模型）的精度也比不含有气温因子的最好的模型（喀什地区的PSO-ELM9模型）高。可以推测，气温因子与ET0的相关性最高，这与李志磊等[21-22]的研究结论一致。

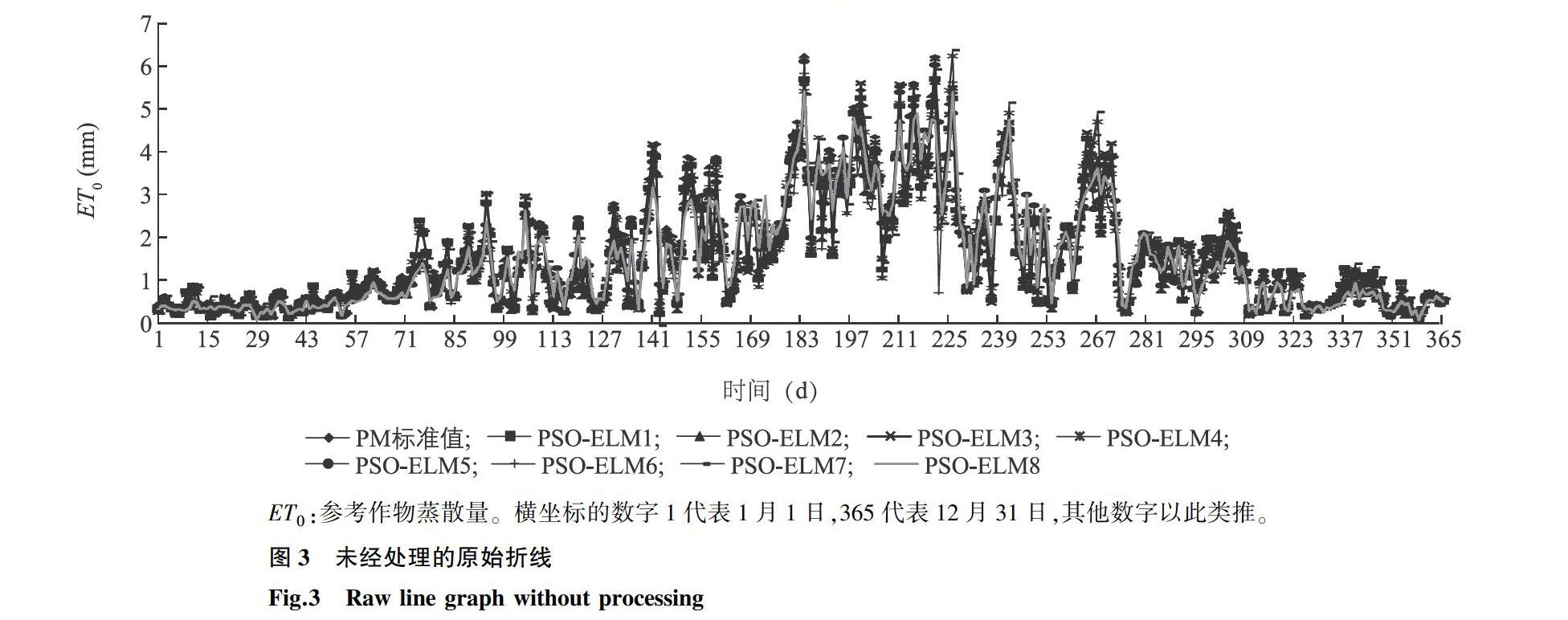
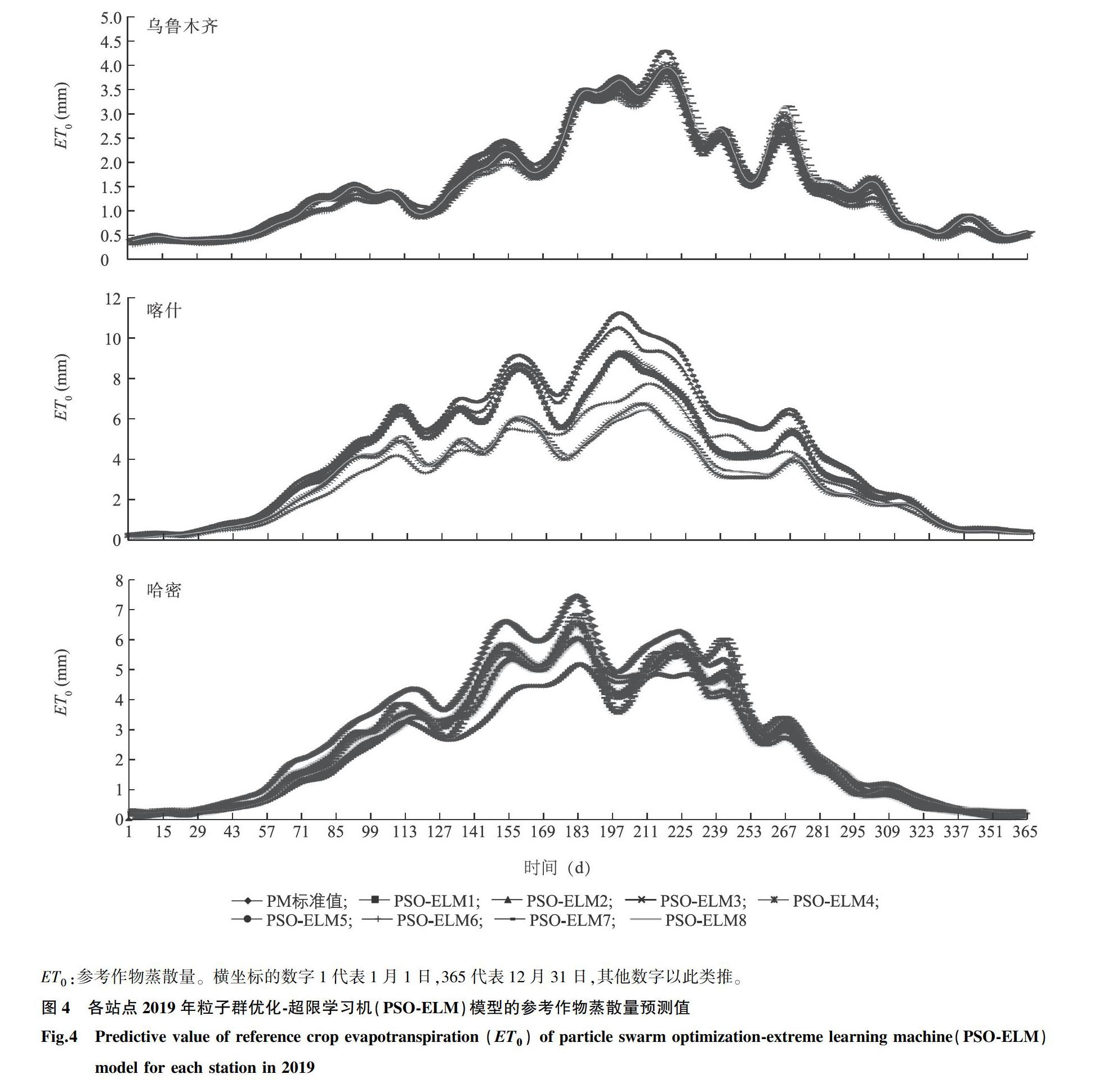
对3个站点基于气温气象因子的8种模型（PSO-ELM1～PSO-ELM8）进行分析。图3为未经处理的原始折线，可见ET0在不同站点及不同模型下波动较大。由于图3具有伪噪声特性，不利于直观展示各个模型与PM标准值的拟合度，因此对预测值进行高斯平滑处理。图4为高斯平滑处理后基于PM标准值的2019年乌鲁木齐站点、喀什站点、哈密站点PSO-ELM模型日ET0的预测曲线，可以看出，各站点ET0表現为喀什站点>哈密站点>乌鲁木齐站点，3个站点的年均ET0需求量分别为4.058 6 mm/d、3.034 6 mm/d、1.573 8 mm/d。如表2所示，3个站点的R2为0.777 0～0.989 2，MAE为0.094 6～1.088 6 mm/d，RMSE为0.131 4～1.588 4 mm/d。

当输入的气象因子数量为5个时，乌鲁木齐站点、喀什站点、哈密站点的PSO-ELM1模型的R2分别为0.989 2、0.985 2、0.949 7，MAE分别为0.094 6 mm/d、0.196 7 mm/d、0.464 7 mm/d，RMSE分别为0.131 4 mm/d、0.390 4 mm/d、0.571 1 mm/d，平均R2=0.974 7，平均MAE=0.252 0 mm/d，平均RMSE=0.364 3 mm/d。虽然哈密站点模型的精度略低于其他2个站点，但相比于其他模型的精度已经达到最高水平。以上结果表明，PSO-ELM1模型的综合判断精度在所有模型中最高，能够精准反映气象因子与ET0之间的关系。

当输入的气象因子数量为4个时，即缺失u2、n、RH其中1个，此时PSO-ELM模型的精度较输入5个气象因子的模型略有下降，在喀什站点PSO-ELM4模型的R2下降了0.220 6，其预测效果相对较差。而在乌鲁木齐站点，PSO-ELM4模型的R2为0.968 5，表明该模型在乌鲁木齐站点的适用性大于喀什站点及哈密站点。PSO-ELM3模型的精度明显优于PSO-ELM2、PSO-ELM4模型，与PSO-ELM1模型相比，R2、MAE、RMSE的差值分别小于0.002 9 mm/d、0.012 6 mm/d、0.097 5 mm/d，可以作为PSO-ELM1的近似模型。乌鲁木齐站点模型按精度排序为PSO-ELM3>PSO-ELM4>PSO-ELM2，其中气象因子u2和RH对模型的正向影响较大，喀什站点、哈密站点模型按精度排序为PSO-ELM3>PSO-ELM2>PSO-ELM4，其中气象因子u2和n对模型的正向影响较大。在本输入因子条件下，3个站点中表现最好的模型均含有u2因子。综合考虑得出，在4个气象因子条件下，气象因子u2是除气温因素外对ET0影响最大的，这与张皓杰等[23]研究得出的除气温因素外u2因素为西北旱区ET0的主要驱动因子的结论一致。

当输入的气象因子数量为3个时，即缺失u2、n、RH其中的2个，PSO-ELM6模型的精度下降最为明显，其中喀什站点、哈密站点的R2分别降至0.794 8、0.808 2，MAE分别提高至1.021 0 mm/d、0.752 5 mm/d，RMSE分别提高至1.588 4 mm/d、1.174 7 mm/d。值得关注是，在喀什地区，与PSO-ELM4模型相比可知，PSO-ELM6模型在缺少输入因子RH的情况下综合指标反而优于PSO-ELM4模型，说明在某些地区增加输入因子不一定能提升预测精度。模型PSO-ELM5在喀什站点、哈密站点表现出较为理想的拟合效果。与PSO-ELM2相比，PSO-ELM5在少了因子n后，3个站点的R2、MAE、RMSE变化较小，表明输入不同气象因子对ET0的影响水平与贡献率大小不同，得出n因子的贡献率较其余2个因子小。PSO-ELM7模型在乌鲁木齐站点的表现优于PSO-ELM5且异于喀什站点、哈密站点的较优模型，MAE、RMSE分别为0.160 0 mm/d、0.242 1 mm/d，是3因子模型中的最优值，表明在乌鲁木齐地区，气象因子RH对ET0的贡献率起主导作用，PSO-ELM7可作为该地区ET0的推荐模型。

当输入的气象因子数量为2个时，即只有Tmax、Tmin2个因子，仅在输入气温因子时模型PSO-ELM8也表现出一定的预测能力，其中乌鲁木齐站点的R2高达0.871 4，MAE為0.326 9 mm/d，RMSE为0.453 9 mm/d，与喀什站点、哈密站点的相关指标相比最好，说明该模型在新疆平均气温较低的地区（乌鲁木齐、喀什、哈密，年均气温分别为8.35 ℃、12.95 ℃、11.00 ℃）适用性好;相对于PSO-ELM6而言少了气象因子n，但相对应的预测精度仅略微下降，这与上文中气温因子和ET0相关性最高的结论一致;在喀什站点，与PSO-ELM7模型相比，PSO-ELM8模型在缺少输入因子RH情况下综合指标反而也优于PSO-ELM7模型，同样印证了上文所提到的结论——在某些地区增加输入因子不一定能提升预测精度。

2.2 PSO-ELM模型与其他模型预测精度的比较分析

以PM公式计算得出的ET0作为标准值，在上述模型精度的评价中选择精度较差的PSO-ELM6模型与ELM、Makkink、I-A 3种模型进行综合对比，Makkink、I-A模型的计算方法分别见公式（2）和公式（3）。

选择气象因子Tmax、Tmin、n作为输入参数。表3显示，3个站点PSO-ELM6模型的R2、MAE、RMSE范围分别为0.794 8～0.907 9、0.274 8～1.021 0 mm/d、0.388 3～1.588 4 mm/d。ELM模型的精度较PSO-ELM6低，其中R2、MAE、RMSE的范围分别为0.704 1～0.897 5、0.287 3～1.106 7 mm/d、0.405 1～1.719 7 mm/d。PSO-ELM6、ELM的GPI分别为1.730 3、0.916 5，结果表明，粒子群优化后的ELM在精度方面有了明显提升。在经验模型方面，虽然乌鲁木齐站点经验模型I-A的R2为0.791 4，小于Makkink的0.857 4，但两者的GPI分别为-1.135 1、-8.880 7，表明I-A模型的综合精度比Makkink模型高。4种模型的GPI排序为PSO-ELM6>ELM>I-A>Makkink。图5为在3个站点由4种不同模型的预测结果与PM公式计算的ET0标准值分布的箱线图，可以看出，PSO-ELM6模型的箱体位置分布、中位线、上下边缘线与PM标准模型非常相近且相似度大于ELM，与I-A、Makkink传统模型相比，机器学习模型提供了更接近PM标准值的ET0分布。根据上述分析可知，基于机器学习的模型比传统经验模型具有更好的性能，与ELM、I-A、Makkink模型相比，PSO-ELM6模型在所有站点提供了最好的ET0预测。

2.3 PSO-ELM模型的普適性分析

由上述分析结果可知，PSO-ELM3模型（输入气象因子为Tmax、Tmin、RH、u2）在输入因子较少的情况下表现出较高精度。为了对模型在新疆地区的普适性进行分析，以PSO-ELM3作为乌鲁木齐、喀什、哈密训练站点的模型，在2018-2019年选取乌鲁木齐、喀什、哈密、阿勒泰、昭苏、和田中的5个站点作为预测站点建立预测模型，共构建15个预测模型。

由表4可知，模型PSO-ELM3在新疆地区各个站点的R2均大于0.905 0，MAE均小于0.456 7 mm/d，RMSE均小于0.596 8 mm/d，其中阿勒泰站点的ET0误差相对较大，平均R2、MAE、RMSE分别为0.923 4、0.345 9 mm/d、0.403 3 mm/d，模型精度稍低，这是由于阿勒泰地区处于较高的纬度且年平均气温（4.25 ℃）与其他站点的差距较大。整体上看，与原始训练站点模型精度对比可知，预测站点的模型预测精度仅略微下降，各个站点间模型的可移植性较好，都达到了较高水平。结果表明，PSO-ELM3模型在新疆各地区的普适性较好，可以将该模型作为预测新疆地区其他站点ET0值的推荐模型。

3 结论

本研究基于粒子群优化算法[29]优化超限学习机的权重和阈值，利用新疆各地区2009-2019年的气象数据建立了1个用于逐日ET0预测的PSO-ELM模型，将该模型用于不同地区的ET0预测。结果表明，PSO-ELM在3个主研究地区的8种气象因子组合条件下都表现出了较好的预测精度，通过与其他模型的对比及普适性分析，验证了该模型在不同地区、不同条件下的适用性和普适性。

对5种不同的气象因子进行组合，得到3个站点的8种不同PSO-ELM模型，不同模型预测乌鲁木齐、喀什、哈密地区ET0的精度有差异，其中PSO-ELM1的预测精度最高，在对应站点的平均R2为0.974 7，MAE、RMSE表现出较小误差（平均MAE=0.252 0 mm/d，平均RMSE=0.364 3 mm/d）。当输入因子数为4个时，模型PSO-ELM2、PSO-ELM3、PSO-ELM4的分析结果表明，在新疆各站点中除气温因子外气象因子u2对ET0预测影响最大，在只有气温因子输入的情况下，模型也能表现出足够的精度。结果表明，PSO-ELM模型在不同气象因子输入组合下是一种能够作为替代PM公式计算ET0的模型。

将使用Tmax、Tmin、n作为气象输入因子的PSO-ELM6、ELM、Makkink、I-A模型与由PM公式计算出的标准值进行对比发现，PSO-ELM6的预测效果好于其他3种模型，乌鲁木齐站点、喀什站点、哈密站点的R2分别为0.907 9、0.794 8、0.808 2，且平均MAE为0.682 8 mm/d，平均RMSE为1.050 5 mm/d，均为最小值。因此PSO-ELM6更适合气象因子（Tmax、Tmin、n）输入条件下乌鲁木齐、喀什、哈密地区的逐日ET0预测。

通过对模型的普适性分析，将乌鲁木齐站点、喀什站点、哈密站点的PSO-ELM3模型应用到疆地区其他站点进行ET0预测，预测结果表现较好，R2为0.920 7～0.982 3，MAE为0.103 4～0.456 6 mm/d，RMSE为0.153 0～0.596 7 mm/d，整体表现出较高的预测精度，表明该模型在新疆不同地区的普适性较好，可以作为新疆缺乏历史数据地区的ET0预测模型使用。

参考文献：

[1] 康绍忠.农业水土工程概论[M].北京：中国农业出版社，2007：115-118.

[2] SHIRI J， NAZEMI A H， SADRADDINI A A，et al. Comparison of heuristic and empirical approaches for estimating reference evapotranspiration from limited inputs in Iran[J]. Computers and Electronics in Agriculture， 2014，108： 230-241.

[3] KISI O， SANIKHANI H， ZOUNEMAT-KERMANI M， et al. Long-term monthly evapotranspiration modeling by several data-driven methods without climatic data[J]. Computers and Electronics in Agriculture， 2015，115： 66-77.

[4] MARTI P， GONZLEZ-ALTOZANO P， LPEZ-URREAR， et al. Modeling reference evapotranspiration with calculated targets. Assessment and implications[J]. Agricultural Water Management， 2015，149： 81-90.

[5] FERREIRA L B， DA CUNHA F F， DE OLIVEIRA R A， et al. Estimation of reference evapotranspiration in Brazil with limited meteorological data using ANN and SVM-A new approach[J]. Journal of Hydrology， 2019， 572： 556-570.

[6] BANDA P， CEMEK B， KUCUKTOPCU E， et al. Estimation of daily reference evapotranspiration by neuro computing techniques using limited data in a semi-arid environment[J]. Archives of Agronomy and Soil Science， 2018， 64（7）： 916-929.

[7] 冀秀梅，王 龙，高克伟，等. 极限学习机在中厚板轧制力预报中的应用[J].钢铁研究学报，2020，32（5）：393-399.

[8] 卢宏亮，赵明松. 基于神经网络模型的安徽省土壤pH预测[J].江苏农业学报，2019，35（5）：1119-1123.

[9] 李 晨，崔宁博，魏新平，等. 改进Hargreaves模型估算川中丘陵区参考作物蒸散量[J].农业工程学报，2015，31（11）： 129-135.

[10]LI H J， XU Q， HE Y S， et al. Prediction of landslide displacement with an ensemble-based extreme learning machine and copula models[J]. Landslides， 2018， 15（10）： 2047-2059.

[11]张 千，魏正英，张育斌，等. 基于烟花算法优化极限学习机的温室参考作物蒸散量预测研究[J].中国农村水利水电，2020（3）：29-32，38.

[12]许伟栋，赵忠盖. 基于卷积神经网络和支持向量机算法的马铃薯表面缺陷检测[J].江苏农业学报，2018，34（6）：1378-1385.

[13]魏 俊，崔宁博，陈雨霖，等. 基于极限学习机模型的中国西北地区参考作物蒸散量预报[J].中国农村水利水电，2018（8）：35-39.

[14]刘小华，魏炳乾，吴立峰，等. 4种人工智能模型在江西省参考作物蒸散量计算中的适用性[J].排灌机械工程学报，2020，38（1）：102-108.

[15]樊湘鹏，许 燕，周建平，等. 遗传算法与小波神经网络在ET0预测中的应用[J].燕山大学学报，2019，43（2）：182-188.

[16]RAWAT K S， SINGH S K， BALA A， et al. Estimation of crop evapotranspiration through spatial distributed crop coefficient in a semi-arid environment[J]. Agricultural Water Management， 2019，213： 922-933.

[17]邢立文，崔宁博，董 娟. 基于LSTM深度学习模型的华北地区参考作物蒸散量预测研究[J].水利水电技术，2019，50（4）：64-72.

[18]李可利，张 鑫. 基于ANFIS的陕西省参考作物蒸散量计算[J].自然资源报，2020，35（6）：1472-1483.

[19]GRANATA F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study[J]. Agricultural Water Management， 2019，217： 303-315.

[20]ANTONOPOULOS V Z， ANTONOPOULOS A V. Daily reference evapotranspiration estimates by artificial neural networks technique and empirical equations using limited input climate variables[J]. Computers and Electronics in Agriculture， 2017，132： 86-96.

[21]李志磊，周建平，魏正英，等. ET0预测的卡尔曼滤波修正ANFIS模型研究[J].干旱地区农业研究，2017，35（3）：114-119.

[22]冯 禹，崔宁博，龚道枝，等. 基于极限学习机的参考作物蒸散量预测模型[J].农业工程学报，2015，31（增刊1）：153-160.

[23]张皓杰，崔宁博，徐 颖，等. 基于ELM的西北旱区参考作物蒸散量预报模型[J].排灌机械工程学报，2018，36（8）：779-784.

[24]吳立峰，鲁向晖，刘小强，等. 蝙蝠算法优化极限学习机模拟参考作物蒸散量[J].排灌机械工程学报，2018，36（9）：802-805，829.

[25]ALLEN R G， PEREIRA L S， RAES D， et al. Crop evapotranspiration： guide-lines for computing crop water requirements[M]//FAO. Irrigation and Drainage. Rome：FAO， 1998.

[26]HUANG G， ZHU Q， SIEW C K， et al. Extreme learning machine： theory and applications[J]. Neurocomputing， 2006， 70（1）： 489-501.

[27]王 俊，刘 刚. 基于粒子群优化聚类的温室无线传感器网络节能方法[J].农业工程学报，2012，28（7）：172-177.

[28]刘环宇，陈海涛，闵诗尧，等. 基于PSO-SVR的植物纤维地膜抗张强度预测研究[J].农业机械学报，2017，48（4）：118-124.

[29]郭亚菲，樊 超，闫洪涛. 基于主成分分析和粒子群优化神经网络的粮食产量预测[J].江苏农业科学，2019，47（19）：241-245.

（责任编辑：徐 艳）