基于模糊贝叶斯证据理论的盾构下穿既有隧道安全风险评价

吴贤国，刘 茜，陈虹宇，曾铁梅，王金峰，陶文涛

(1.华中科技大学土木与水利工程学院，湖北 武汉 430074；2.新加坡南洋理工大学土木工程与环境学院，新加坡 639798；3.武汉地铁集团有限公司，湖北 武汉 430040)

0 引言

近年来，我国地下轨道网线越来越密集，新建隧道下穿既有隧道的情况也越来越普遍。当盾构下穿既有隧道时，会不可避免地引起土层的扰动和变形，从而诱发既有隧道产生沉降变形，严重时会影响既有隧道的正常运营。因此，对盾构下穿既有隧道的安全风险进行有效评估，及时进行施工安全控制具有重要的工程意义。

目前，国内外学者已经对盾构下穿隧道施工的影响和安全控制进行了一些研究。杨春山等[1]借助大型有限元软件进行施工模拟，对新建隧道盾构掘进过程引起既有隧道的位移变化进行了分析。金大龙[2]基于多种理论分析和模型试验，对盾构隧道群下穿既有运营隧道的变形影响和控制问题进行了深入研究。马文辉等[3]基于有限元分析软件，总结了近距离下穿既有地铁盾构隧道的施工参数控制经验。杨建烽等[4]通过数值模拟分析，对盾构下穿既有地铁区间隧道的沉降控制进行了研究。Yin等[5]采用三维有限元方法研究了下穿盾构隧道开挖间隙对既有盾构隧道结构沉降的影响。Lai等[6]基于监测数据和有限差分法数值模拟，对下穿隧道引起的既有隧道沉降行为进行了深入研究。还有学者基于模糊故障树分析、突变理论和模糊综合评价等方法，从风险分析评估的角度对隧道近接施工的安全问题进行了相关研究[7-9]。然而，上述研究中数值模拟和模型试验方法往往是通过假设和简化来进行建模分析，相较于实际情况会存在较大差距，且工作量大，精确度浮动性较大；而模糊故障树分析和模糊综合评价等方法没有综合考虑多源风险因素的模糊性、随机性和不确定性，且过程中对于指标权重的确定过于主观，难以实现较好的隧道施工风险预警与控制。

为此，本文将模糊贝叶斯和证据理论相结合，提出一种基于模糊贝叶斯证据理论模型的盾构下穿既有隧道安全风险评价方法。首先，将盾构下穿施工对既有隧道安全的主要影响因素进行分析；然后，结合工程经验和专家知识建立贝叶斯网络，并引入证据理论对专家评价进行有效融合，以获得根节点先验概率；最后，在构建的模糊贝叶斯网络模型基础上进行风险概率推理与敏感性分析，对工程的安全风险进行评估并确定关键的敏感因素，从而有助于工程的安全风险预警与控制。本文提出的方法不仅模型结构简单，易于表达，可以对模糊问题和不确定性问题进行建模，而且能够综合不同专家或数据源的知识或信息，实现更准确的风险建模和评价。

1 方法及原理

1.1 贝叶斯网络

贝叶斯网络(bayesian networks,BN)也称为贝叶斯信度网络(bayesian belief networks)，它通过有向无环图来反映具体问题中复杂变量之间的连接关系，是一种基于概率理论的网络模型[10]。贝叶斯网络本质是概率值的推理计算。对于贝叶斯网络中任意随机变量X=(xt1,xt2,…,xtn)，相应的联合概率分布可表示为

f(xt1,xt2,…,xtn)=∀tj∈tf(xtj|Xpa(tj))。

(1)

式中：Xpa(tj)为随机变量X在时期tj的父节点集合；t为时期长度。

如果随机变量X为时间序列，且xtj的父节点为(xtj-1,…,xt1)，则式(1)可转换为

f(xt1,xt2,…,xtn)=∀tj∈tf(xtj|xt1,…,xtj-1)。

(2)

根据概率论中的链规则，即联合概率可以由其条件概率链表达，则式(2)右端的条件概率函数可构建为

(3)

1.2 证据理论

证据理论是一套关于证据推理的数学理论，可以很好地表现问题的未知性和不确定性[11]。证据理论可以综合不同专家或数据源的知识或信息，能有效处理不确定知识，在多传感器信息融合、检测诊断等领域具有广泛的应用。

1)定义1：假设论域Θ={θ1,θ2,…,θM}是1个元素个数有限且元素两两互斥的集合，则将Θ称为识别框架，Θ的所有子集而组成的集合称为Θ的幂集，记作2Θ。

2)定义2：识别框架Θ的基本概率分配函数(BPA)m是一个从集合2Θ到[0,1]的映射，且满足

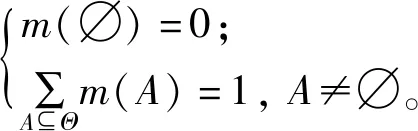
(4)

其中:∅为空集；A为Θ的任意子集，记作A⊆Θ；m(A)为命题A的基本信任分配函数。

3)定义3：假设识别框架Θ内有n组独立的证据{m1,m2,…,mn}，Ai,Aj,…,Ak(i,j,…,k=1,2,…，n)表示n组独立证据的焦元，则利用Dempster合成规则进行证据融合，可表达为：

(5)

K=∑Ai∩Aj∩…∩Ak=∅m1(Ai)·m2(Aj)…mn(Ak)。

(6)

式中K为各条证据之间的冲突系数，衡量了证据之间的冲突程度。

2 基于模糊贝叶斯证据理论的安全风险评价模型

本文提出一种将模糊贝叶斯网络和改进证据理论相结合的安全风险评价模型，评价流程如图1所示。该方法包括4个主要阶段：1)贝叶斯网络设计，2)专家评价模糊化，3)基于改进证据理论的区间融合，4)风险概率推理及分析。基于模糊贝叶斯网络与证据理论对盾构下穿既有隧道的安全风险进行评价，可以有效解决评价过程中的不确定性问题和推理问题，从而得到更加可靠和全面的评价结果。

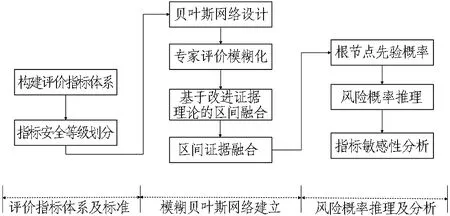
图1 基于模糊贝叶斯证据理论的盾构下穿既有隧道安全风险评价流程Fig.1 Safety risk assessment process of shield tunneling underneath existing tunnel based on fuzzy Bayesian network and evidence theory

2.1 评价指标体系及标准

盾构下穿既有隧道的安全评价是一个复杂的不确定推理问题，涉及到众多因素。通过分析相关文献，提炼出盾构下穿既有隧道安全风险的主要影响因素，包括新建隧道参数设计B1、土体条件B2、既有隧道条件B3、施工与管理条件B44类，以此构建盾构下穿既有隧道安全评价指标体系。

1)新建隧道参数设计B1。新建隧道相关参数的设计是影响周围土体和构筑物非常重要的一类因素，它可以反映隧道开挖的大致情况。新建隧道相关参数一般主要考虑新建隧道直径(X1)、两隧道的净距(X2)以及两隧道的平面夹角(X3)3个参数[12-13]。

2)土体条件B2。土体作为新建隧道与既有隧道相互作用的中间媒介，土体条件对于盾构下穿引起既有隧道的变形破坏有着至关重要的作用[14]。其中，压缩模量(X4)、黏聚力(X5)、内摩擦角(X6)和泊松比(X7)是表征土体条件的几个常见影响因素。

3)既有隧道条件B3。既有隧道的变形破坏不仅与外部环境影响有关，而且与自身现有的条件也有很大的关系。既有隧道埋深(X8)、既有隧道直径(X9)和覆跨比(X10)会影响既有隧道的基底应力变化，从而影响隧道的变形[15]。此外，既有隧道健康状态(X11)反映了隧道结构目前渗漏水、开裂及沉降等病害情况，对于既有隧道的变形程度也有较大影响，在一定程度上决定了隧道承受变形的能力。

4)施工与管理条件B4。盾构隧道的施工过程是一个人-机-环综合作用的系统工程，人为因素的管理条件也是工程安全需要考虑的重要因素之一[16]。本文通过施工技术的复杂性(X12)、施工环境的复杂性(X13)和施工协调的复杂性(X14)来表征工程的施工与管理水平。

为了更好地对盾构下穿既有隧道的风险指标进行评价，需要对指标的安全等级进行划分。依据相关研究成果，并参考相关规范[17-19]的要求，将盾构下穿既有隧道安全风险评价指标等级状态划分为安全(Ⅴ级)、较安全(Ⅳ级)、一般(Ⅲ级)、较危险(Ⅱ级)、危险(Ⅰ级)5个等级。其中，客观因素的划分由实际工程中的具体测量值进行衡量，主观因素的划分由领域专家结合百分制进行衡量。评价指标安全等级划分及其量值范围如表1所示。

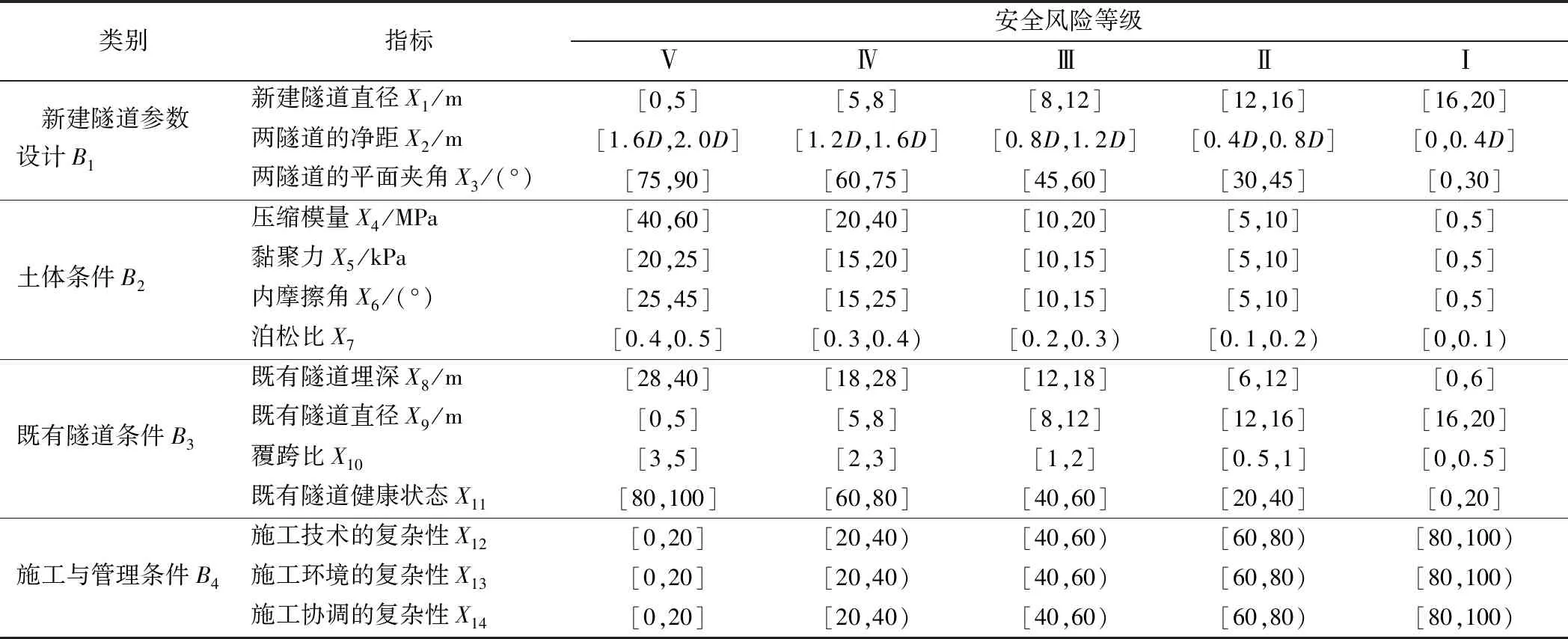
表1 评价指标安全等级划分及其量值范围Table 1 Classification of safety grade of evaluation index and its range of value

2.2 模糊贝叶斯网络建立

2.2.1 贝叶斯网络设计

贝叶斯网络设计通常有基于专家知识的人工建模和基于大量数据的学习建模2种方法，由于缺乏盾构下穿既有隧道的大量样本数据，所以本文采用人工建模的方法来进行贝叶斯网络设计。贝叶斯网络模型由网络结构和网络参数2部分组成，因此，构建贝叶斯网络需要进行结构设计和概率参数设计。首先，根据评价指标体系和风险等级划分，确定贝叶斯网络节点和节点状态；然后，在专家知识和大量工程实践经验的基础上，对模糊贝叶斯网络进行条件概率设计，并根据因素间的相互影响关系，结合工程实际情况，采用故障树向贝叶斯网络转化来进行结构设计，根节点的先验概率则通过专家群决策法得到，具体如下文所述。

2.2.2 先验概率获取

在没有大量精确统计数据的情况下，本文采用专家群决策法来获取根节点的模糊先验概率，具体流程为:

1)将专家语言评价值分为5个风险等级，分别为安全、较安全、一般、较危险、危险，对应的量化值x分别定义为0.1、0.3、0.5、0.7、0.9。

2)邀请几位领域专家，根据自己的工程经验和知识对各个根节点所处的风险等级给出语言值评价，以及对此等级的不确定度。

3)利用模糊隶属函数将专家的语言值评价转换成模糊区间值，从而对专家评价进行模糊化。本文选择高斯隶属函数，它能够反映非线性正态分布特性，其表达式为

(7)

式中：x为专家评价对应的量化值；μ为函数的中心；σ为标准偏差，表示函数的均方根(RMS)宽度。

本文令5个风险等级的高斯隶属函数中心分别为0、0.25、0.5、0.75、1，则每个等级可得到对应的隶属函数。

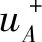
(8)

式中α为常数，且α∈[1,+∞)。

2.2.3 基于改进证据理论的区间融合

2.2.3.1 有效性和规范性检验

专家评价的区间模糊集可直接转换成证据理论中的区间基本概率赋值函数，但在进行区间证据融合前，需要先对区间基本概率赋值函数的有效性和规范性进行检验和修改，使其满足区间基本概率赋值函数的定义，才能进行区间融合。

2.2.3.2 改进的区间证据合成

经典的证据理论合成规则存在一定的缺陷，为了最大限度地减少高冲突证据的负面影响，基于证据可信度提出一种改进的混合区间证据合成规则，具体步骤如下。

1)证据冲突检测

根据经典证据理论，n个证据体之间的冲突程度以冲突系数K表示。

K=∑Aj1∩Aj2∩…∩Ajn=∅m1(Aj1)m2(Aj2)…mn(Ajn)。

(9)

式中Ajn(j=1,2,…,n)为第n个证据体的第j个焦元。

为了区分证据间的冲突程度，以便采用不同的融合规则，设置1个阈值ε对冲突系数K进行冲突检测。当K≥ε时，为高冲突情况，采用改进合成规则进行融合；否则，采用经典的证据理论合成规则进行融合。本文根据统计习惯，将阈值ε设置为1-0.05=0.95。

2)低冲突证据融合

冲突系数K<0.95时为低冲突情况，证据间的冲突可被接受，采用经典的证据理论合成规则进行融合，对于区间基本概率赋值函数m1,m2,…,mn，合成后的区间值下限min(m1⊕m2⊕…⊕mn)(A)和上限max(m1⊕m2⊕…⊕mn)(A)由式(10)确定。

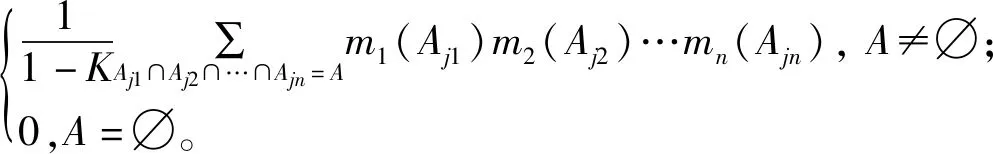
(10)

3)基于高冲突证据的改进合成规则

冲突系数K≥0.95时为高冲突证据情况，为了规避经典证据理论合成规则在高冲突证据下易得到与事实相悖的缺陷，基于证据的可信度重新定义冲突信息的分配，得到新的证据合成规则，具体算法如下。

①步骤1：通过计算证据的支持度获取证据的可信度。

根据式(11)计算证据mi和mj之间的距离dij，然后计算证据mi的支持度Sup(mi)，证据mi的可信度crdei通过Sup(mi)归一化得到，具体如式(12)所示。

(11)

(12)

可以看出，若1个证据与其他证据的相似度越高，则说明该证据被其他证据所支持的程度越高，该证据就越可信，反之亦然。

②步骤2：根据证据可信度分配冲突信息，得到新的区间证据合成规则。

根据可信度将冲突信息按比例分配给证据，对于区间基本概率赋值函数m1,m2,…,mn，合成后的区间值下限和上限由式(13)确定。

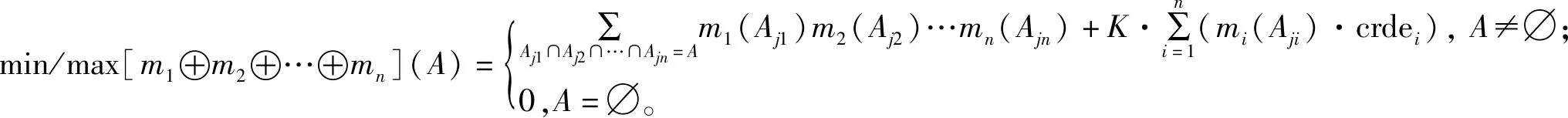
(13)

2.3 风险概率推理与分析

2.3.1 风险概率推理

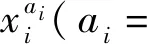
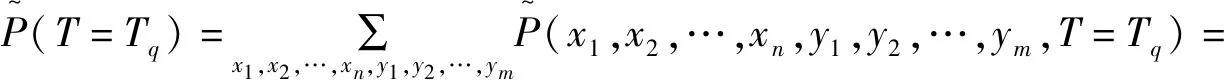
(14)

2.3.2 敏感性分析

敏感性分析能够反映叶节点对于根节点微小变化的敏感程度，从而确定对风险事件贡献度较大的关键风险因素，为风险管控提供理论依据。节点xi对于叶节点T风险等级为Tq的敏感度如式(15)所示。

(15)

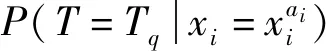
3 实例分析

3.1 工程概况

武汉市某地铁1期工程总长16.7 km，中间贯穿了多个经济带，是连接长江两岸的重要交通线路。1期工程中间下穿了另一条已运营4年的既建轨道交通线路，交角约为21°，2条线路相交后又并行了约200 m。相交区段新建隧道直径约为6 m，既建隧道直径约为8 m。2条隧道相交区段中间的夹层土体主要为淤泥质粉质黏土和粉质黏土，内摩擦角为7.6～16.5°，上覆土体为杂填土和黏土，新建隧道下层土体为粉细砂混砾卵石和强风化含粉砂泥岩。工程施工环境复杂程度和技术难度适中，较易进行工程施工协调。

3.2 构建贝叶斯网络

3.2.1 节点状态划分

结合2.1节中对盾构下穿既有隧道安全风险的等级划分，将贝叶斯网络中各节点划分为1、2、3、4、5这5种状态，使其能够与安全风险等级状态的安全(Ⅴ级)、较安全(Ⅳ级)、一般(Ⅲ级)、较危险(Ⅱ级)、危险(Ⅰ级)一一对应，以方便后文的安全风险评价与分析。

3.2.2 贝叶斯网络设计

根据2.1节构建的评价指标体系，结合贝叶斯网络设计的思路和具体做法，整合事故树及专家经验等先验知识，得到盾构下穿既有隧道安全评价的贝叶斯网络拓扑结构，并对网络的中间节点和叶节点的条件概率表进行设计，具体模型结构如图2所示。

3.3 根节点先验概率获取

由于工程中无大量精确的统计资料，因此,本文通过专家群决策法来获取根节点的先验概率。根据前文所述专家评价方法，邀请3位领域专家结合自己的工程经验和知识对贝叶斯网络中各个根节点指标所处的风险等级给出语言值评价，以及对此等级的不确定度，然后根据式(7)和式(8)利用模糊隶属函数将专家的语言值评价转换成模糊区间值。3位专家的具体评价如表2—4所示。

通过模糊隶属函数对专家评价进行模糊化处理得到模糊区间值后，为了能够基于证据理论进行区间融合，必须先对区间值进行有效性、规范性检验和修改，再根据本文所提出的改进的混合区间证据合成规则对3位专家的评价区间值进行融合。首先，根据式(9)计算证据体之间的冲突系数K；然后，根据阈值ε=0.95判断证据融合应该选用的融合规则。若K<0.95则根据式(10)采用经典证据理论合成规则进行区间融合；否则采用基于证据可信度的改进合成规则，先根据式(11)和式(12)计算出证据的可信度，再根据式(13)基于可信度将冲突信息按比例分配给证据，从而实现区间证据融合。基于改进证据理论对3位专家评价区间值进行融合，得到的结果如表5所示。

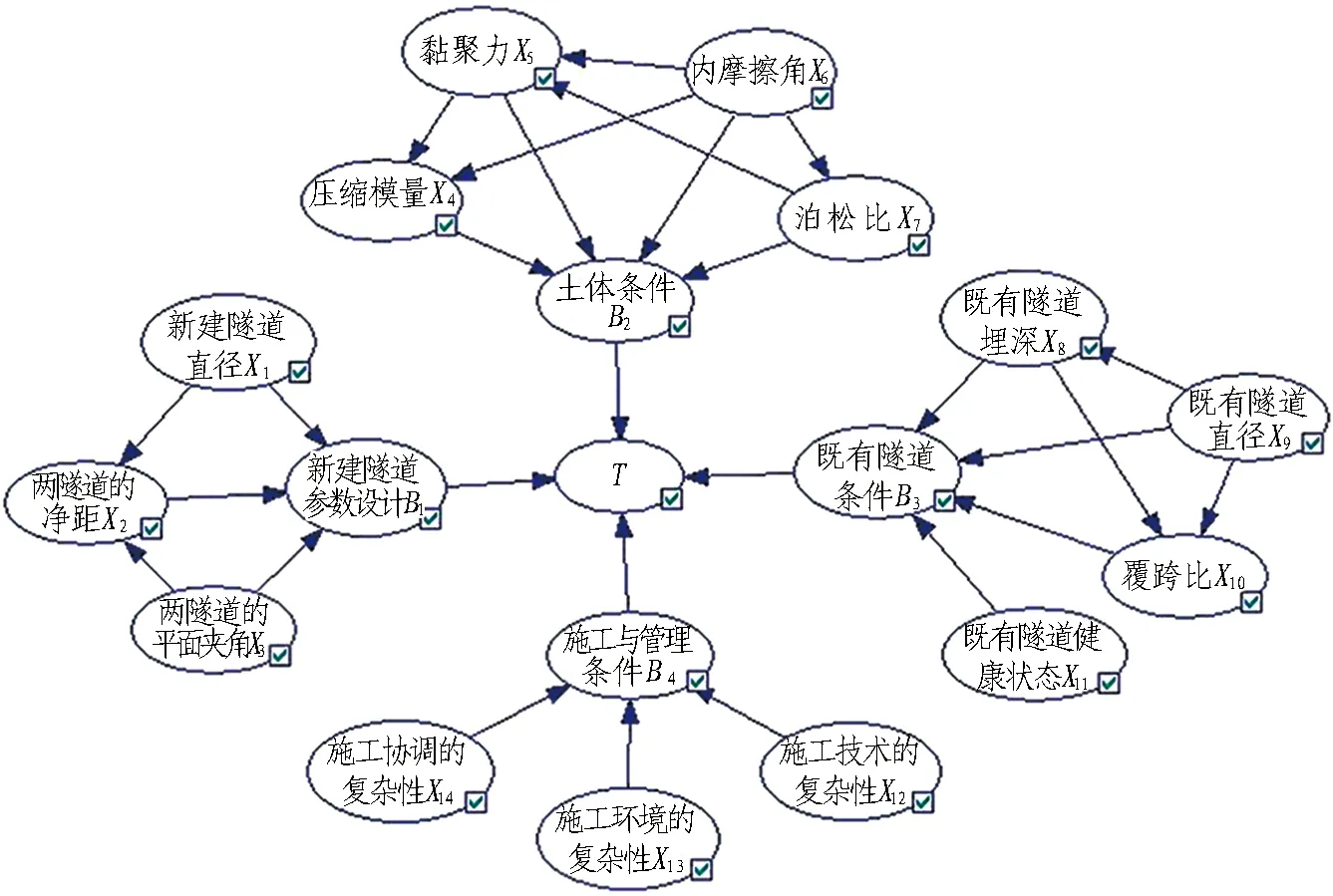
图2 盾构下穿既有隧道安全评价贝叶斯网络模型Fig.2 Bayesian network model for safety assessment of shield tunneling underneath existing tunnels

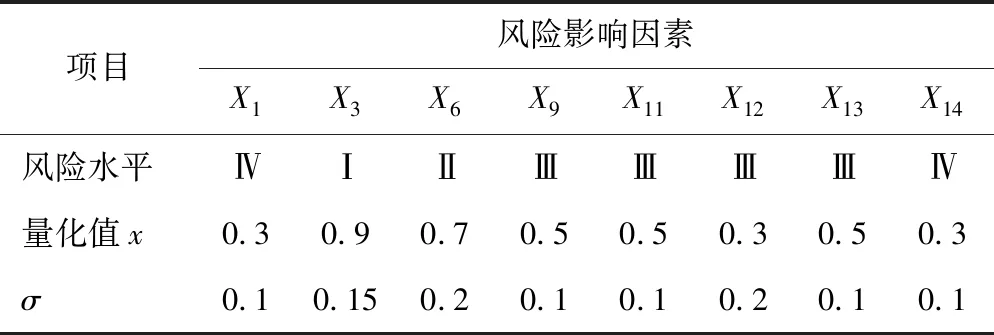
表2 专家1评价Table 2 Evaluation of Expert 1

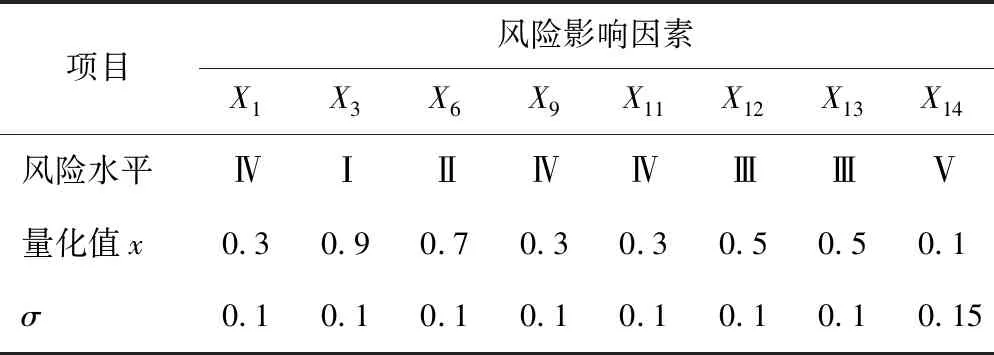
表3 专家2评价Table 3 Evaluation of Expert 2

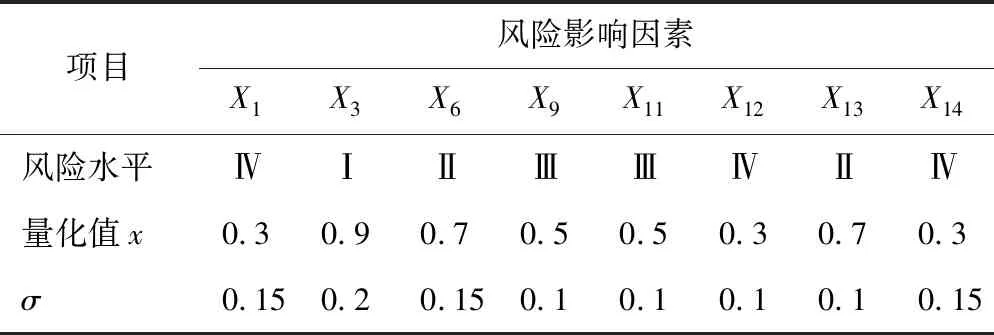
表4 专家3评价Table 4 Evaluation of Expert 3

3.4 风险评价

3.4.1 风险概率推理

在已知根节点先验概率以及中间节点和叶节点条件概率的情况下，通过贝叶斯网络推理可以将根节点的不确定性在网络中进行传递，从而得到叶节点在各个风险等级状态下的概率区间。在表5的基础上，根据式(14)推算得到叶节点T和中间节点B1、B2、B3、B4在各个风险等级状态下的平均概率。计算结果如表6所示。

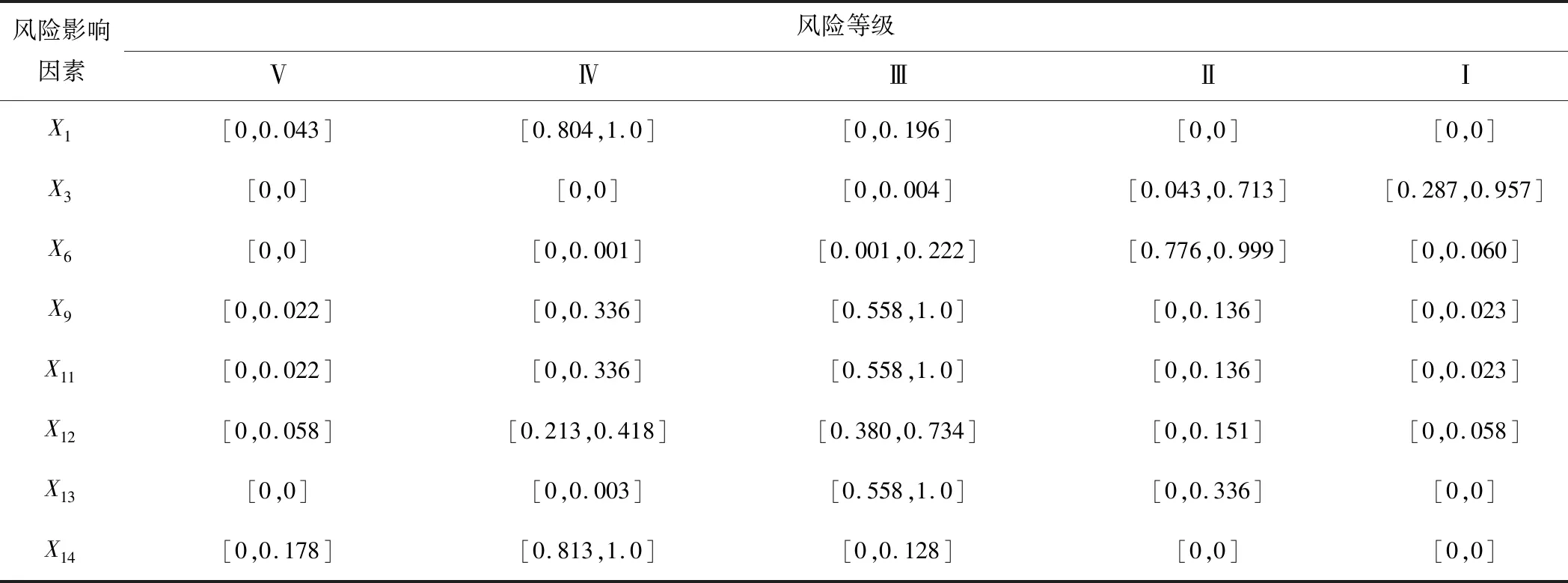
表5 区间证据融合结果Table 5 Fusion results of interval evidence

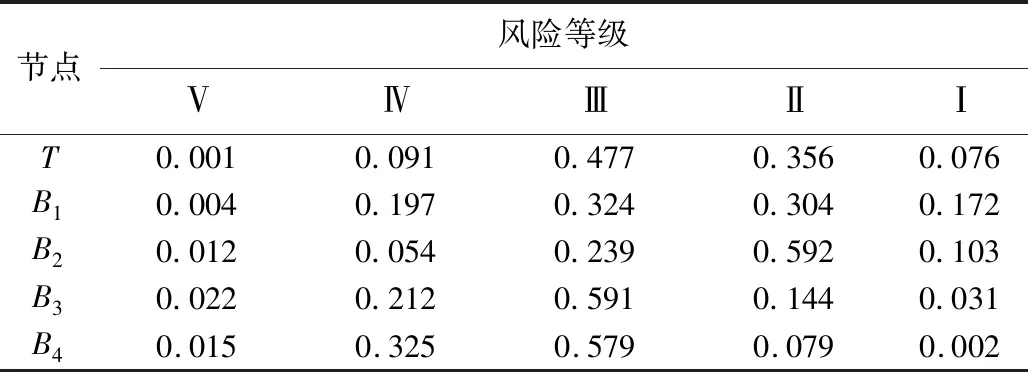
表6 节点的风险概率Table 6 Risk probability of Bi and T

由表6可知，叶节点T风险状态为Ⅲ级的平均风险概率最大，为0.477，对于风险状态为Ⅱ级的平均风险概率也较大，为0.356。因此，可以判断该工程盾构下穿既有隧道安全风险等级为一般(Ⅲ级)，但有向较危险(Ⅱ级)发展的趋势，需要加强关注并采取一定的措施进行管控。

同理分析可得:B1的安全风险等级为一般(Ⅲ级)，但有向较危险(Ⅱ级)发展的趋势；B2的安全风险等级为较危险(Ⅱ级)；B3和B4的安全风险等级均为一般(Ⅲ级)。因此，对于B3和B4方面的风险因素应当加强监控，而对于B1和B2方面的风险因素则应采取适当的安全措施以降低其安全风险。

3.4.2 敏感性分析

敏感性分析可以帮助管理人员辨识关键致险因素，辅助进行安全控制决策。本文按照概率区间的均值进行计算分析，根据式(15)计算14个风险因素对于叶节点T为较高风险等级(T=1、2、3)下的敏感度。为了方便分析，将每个风险因素的敏感度进行数字平均化，如图3所示。

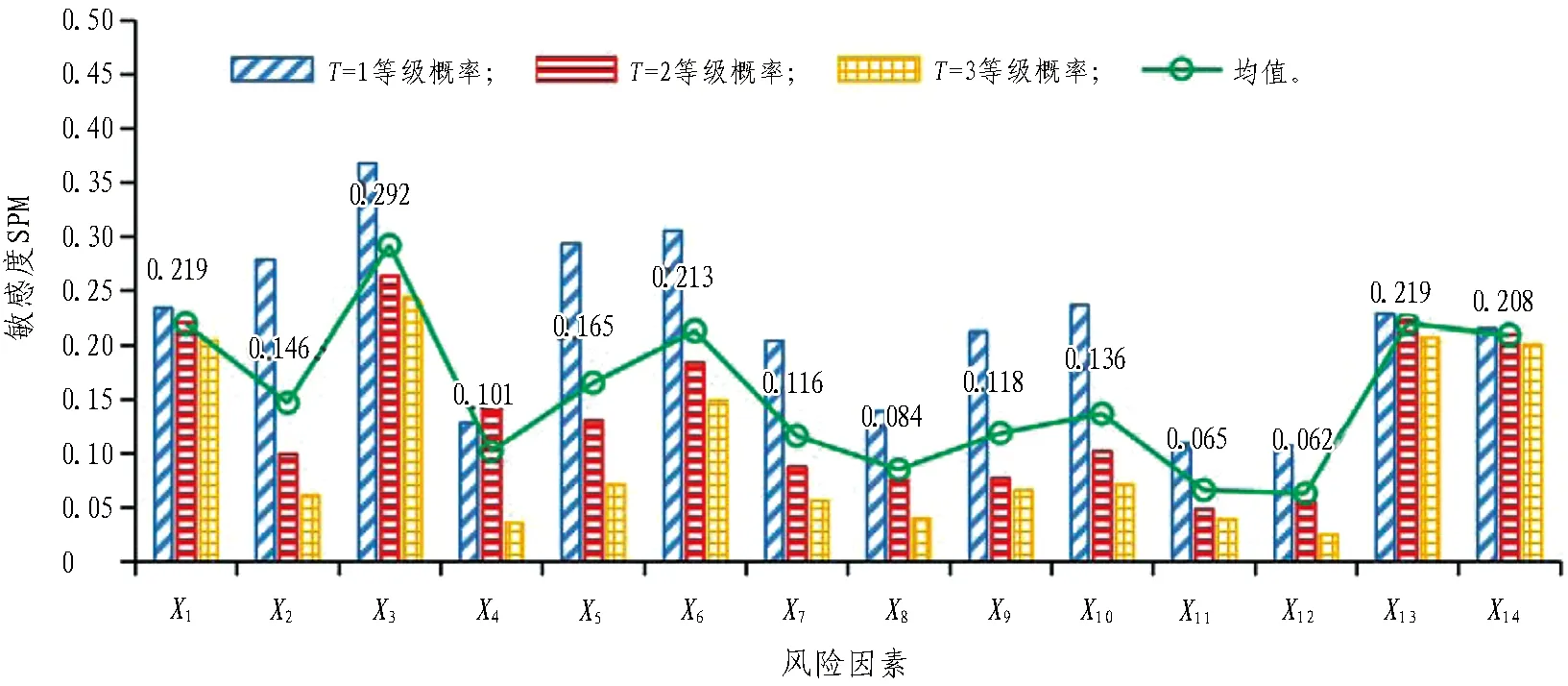
图3 14个风险因素的敏感性分析Fig.3 Sensitivity analysis of 14 risk factors

由图3可知：当安全风险等级为危险(Ⅰ级)时，X3(两隧道的平面夹角)和X6(内摩擦角)的敏感性明显高于其他因素；当安全风险等级为较危险(Ⅱ级)和一般(Ⅲ级)时，X1(新建隧道直径)、X3(两隧道的平面夹角)、X13(施工环境的复杂性)和X14(施工协调的复杂性)的敏感性最大。同时，由图3可知，X1(新建隧道直径)、X3(两隧道的平面夹角)、X6(内摩擦角)、X13(施工环境的复杂性)和X14(施工协调的复杂性)这5个因素对于3个风险等级的敏感性均值排在最前面。因此，当盾构下穿既有隧道安全风险为较高风险等级(T=1、2、3)时，上述5个风险因素应当作为工程重点关注的因素，采取相应的决策对其进行管控，直至潜在安全风险得以控制。

4 结论与讨论

本文提出一套基于模糊贝叶斯和证据理论的盾构下穿既有隧道安全风险评价方法，依托武汉某盾构下穿既有隧道工程进行实证研究，并得出以下结论。

1)在先验知识基础上构建了盾构下穿既有隧道安全评价的贝叶斯网络拓扑结构，基于专家评价结合证据理论融合获取了风险因素的先验概率，从而构建了基于模糊贝叶斯和证据理论的盾构下穿既有隧道安全风险评价模型。

2)基于改进证据理论对专家评价进行融合，通过贝叶斯网络进行风险概率推理，确定本工程盾构下穿既有隧道安全风险等级为一般(Ⅲ级)，但有向较危险(Ⅱ级)发展的趋势，实现了盾构下穿既有隧道施工前阶段的风险评价。

3)在模糊贝叶斯网络的基础上进行敏感性分析，确定了施工前对工程安全风险较为敏感的5个关键因素，分别为X1(新建隧道直径)、X3(两隧道的平面夹角)、X6(内摩擦角)、X13(施工环境的复杂性)和X14(施工协调的复杂性)，为工程的安全控制决策与措施制订提供了依据。当安全风险等级较高时，可以针对这几个因素采取相应的管控措施，如调整两隧道的平面夹角为70～90°，或采取土体注浆法来保持新建隧道与既有隧道之间土体的稳定性等。

本文建立的安全风险评价指标中对土体条件的考虑较为简单，在未来的研究中，可考虑上覆土体条件、上下隧道夹层和周边土体条件及下层地质条件，使风险评价模型更接近实际工程。