满装圆柱滚子轴承自锁必要条件分析
2021-07-22杨凯文潘隆刘高杰赵琳郭志刚
杨凯文,潘隆,2,刘高杰,2,赵琳,郭志刚
(1.洛阳LYC轴承有限公司,河南 洛阳 471039;2.航空精密轴承国家重点实验室,河南 洛阳 471039;3.河南中原特钢装备制造有限公司,河南 济源 454650)
满滚子径向自锁轴承是一种滚子相互锁紧,不会沿径向掉出的圆柱滚子轴承。该类轴承滚子数多,载荷容量大,无保持架,结构简单[1],在低速重载场合应用越来越广泛。受安装空间及结构尺寸的限制,很多轴承无法采用满装自锁结构。文献[1-6]介绍了满滚子径向自锁轴承自锁量及圆周总间隙量的计算方法,在轴承设计时需多次试算调整,同时计算中要兼顾套圈壁厚。没有类似尺寸设计经验的轴承能否采用满装自锁结构,需试算多种主参数,效率低。为便于设计,提出了圆柱滚子轴承径向自锁的必要条件判定公式和图表判定法。
1 锁量和圆周总间隙计算方法
在保证自锁的前提下,锁量不可太大,否则难以从径向装入最后一粒滚子,轴承旋转灵活性也较差,应保证一定的圆周总间隙。在计算前,往往需要根据工程经验先确定锁量和圆周总间隙。
根据轴承外形尺寸及约束条件初步设计轴承滚子组节圆直径Dpw、滚子直径Dw和滚子数Z,由几何关系可得锁量为[1]
(1)
圆周总间隙为[1]
(2)
将滚子组节圆直径最小值、滚子直径最大值和滚子数代入(1),(2)式可得最大锁量和最小圆周总间隙,将滚子组节圆直径最大值、滚子直径最小值和滚子数代入(1),(2)式可得最小锁量和最大圆周总间隙。判断锁量和圆周总间隙是否在预设范围,若不在,需调整滚子直径、滚子组节圆直径和滚子数,重复上述计算,直到满足锁量和圆周总间隙。
2 轴承自锁设计的必要条件
对于给定的尺寸空间,轴承自锁设计都要经过上述试算过程。但对于某些轴承,通过多次调整主参数,反复计算,仍无法找到一组满足预设锁量的主参数,故有必要进行自锁设计前的必要条件判断。
滚子紧密排列的局部圆周分布如图1所示(A,B,C为滚子圆心),存在如下几何关系
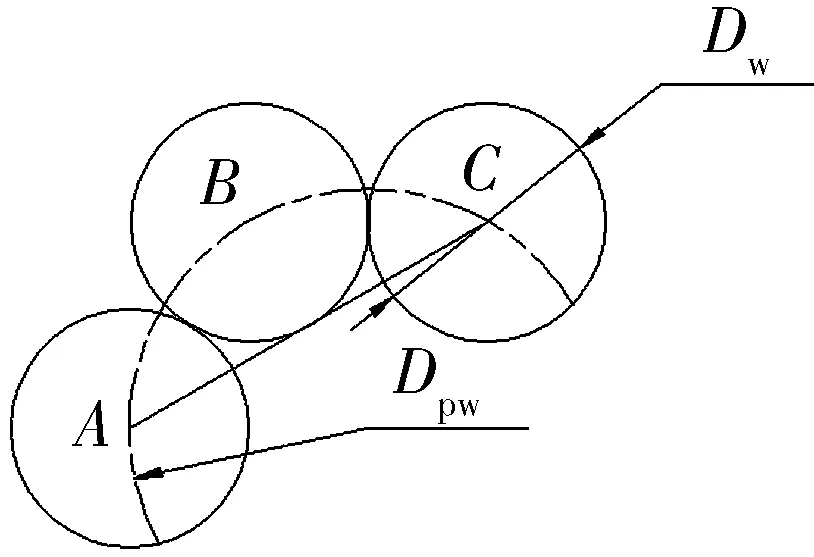
图1 滚子无间隙沿圆周方向排列
(3)
当圆周总间隙为0时,锁量最大,此时,滚子之间彼此紧挨,每个滚子的锁量相等且均为最大锁量。图1中,
(4)
极限锁量为
(5)
此时圆周总间隙为0,联立(3),(5)式可得
(6)
实际上轴承滚子并非无间隙排列,(6)式计算的锁量ε并不是轴承最大锁量,而是一种假设滚子无间隙排列时的极限锁量,即一定直径、个数的滚子组合在一起能够形成的最大锁量。由(6)式可得滚子数
(7)
滚子直径
(8)
计算得到的滚子数可能不是整数,也不是轴承实际滚子数,但可以作为一定锁量和滚子直径下轴承滚子数的极大值。由(6)式可知滚子直径一定时,滚子数增多,无间隙排列滚子组锁量减小,而滚子数一定的轴承锁量不可能大于同样个数和直径的紧密排列滚子组的锁量。若要使轴承锁量大于某一值,将这一锁量代入(7)式,轴承滚子数Z需小于(7)式计算得到的滚子数极大值,即
(9)
同理,由(6)式可知滚子数一定时,若要使轴承锁量大于某一值,滚子直径需满足
(10)
在给定空间内,初步设计滚子直径、滚子数和锁量,代入(9),(10)式,若不成立,说明这组参数无法满足预定锁量。由(3),(9)式可得
(11)
(11)式可作为自锁必要条件中关于滚子直径和滚子组节圆直径的判定公式。(9)—(11)式涉及的参数不同,可以择一使用。
在自锁必要条件判定时,可将设定锁量及滚子数代入(8)式计算一定锁量时的滚子直径。滚子数变化时,可得滚子直径随滚子数的变化曲线。文献[2]设计实例中滚子无间隙排列最大锁量为0.51 mm,若将必要条件计算时的锁量设定为0.3~0.6 mm,可以根据锁量得到一组滚子直径与个数的对应值,见表1(仅给出部分数据),根据数据绘制一组曲线,如图2所示(仅给出部分曲线)。
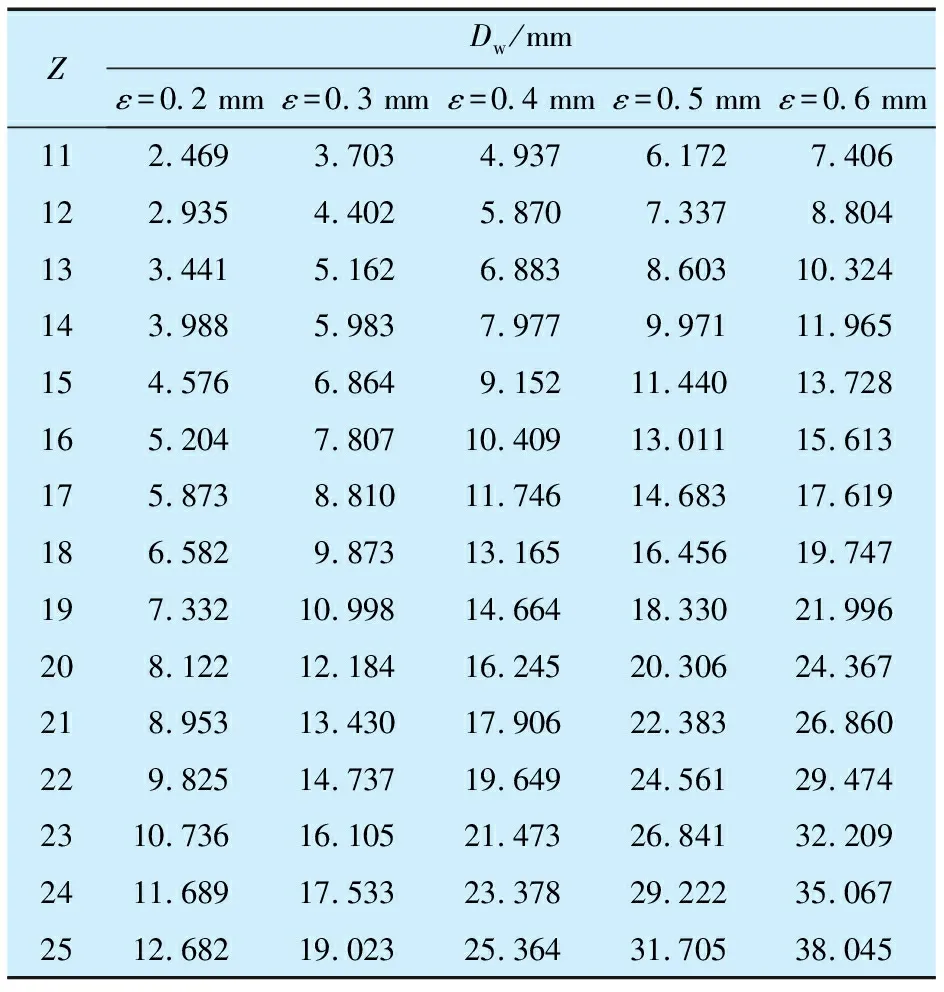
表1 一定锁量时无间隙排列滚子直径与个数
由图2可知:滚子直径一定时,滚子数越多,无间隙排列滚子组能够形成的最大锁量越小;滚子数一定时,滚子直径越大,紧密排列的滚子组能够形成的最大锁量越大;锁量设定后,对于无间隙排列的滚子,滚子直径随滚子数增大而增大,滚子数确定后,滚子直径随之确定。
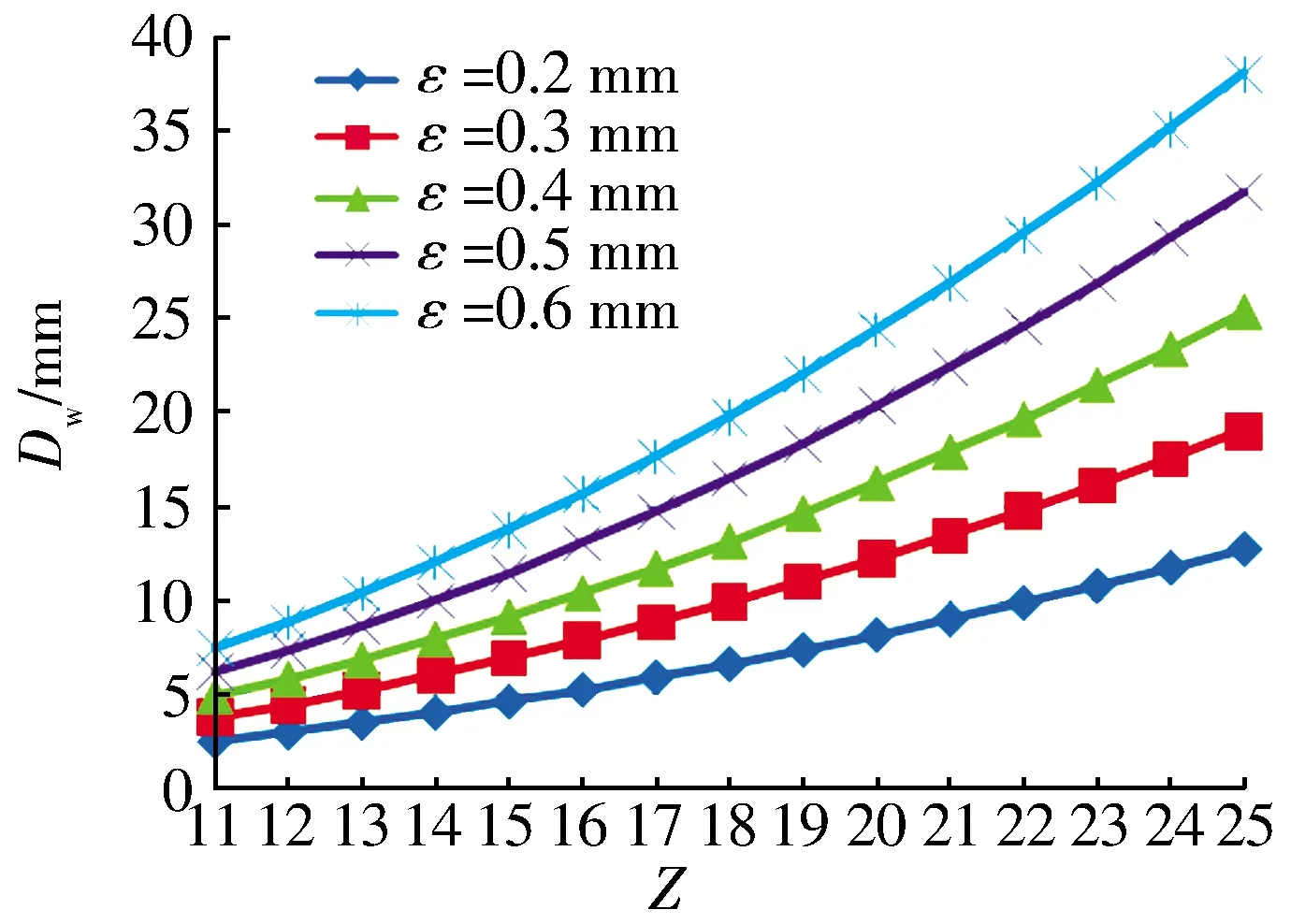
图2 一定锁量时无间隙排列滚子直径与个数的关系
采用上述方法确定的滚子直径与个数的轴承无论滚子组节圆直径取多少,滚子组所能形成的最大锁量不会超过设定值。在给定空间内,要在一定截面尺寸内设计满装自锁轴承需要满足滚子直径与个数的匹配关系才能实现。实际设计中,可以根据工程经验确定合理锁量范围。通过(6)式计算或查询滚子直径与个数关系图获得不同主参数组合能够形成的最大锁量,由此判断所设计轴承参数是否满足自锁必要条件。
锁量一定时,滚子直径、滚子数确定后,可以计算得到无间隙排列的滚子组节圆直径,即得到滚子数与滚子组节圆直径的对应值,见表2(仅给出部分数据),根据数据绘制一组曲线,如图3所示(仅给出部分曲线)。
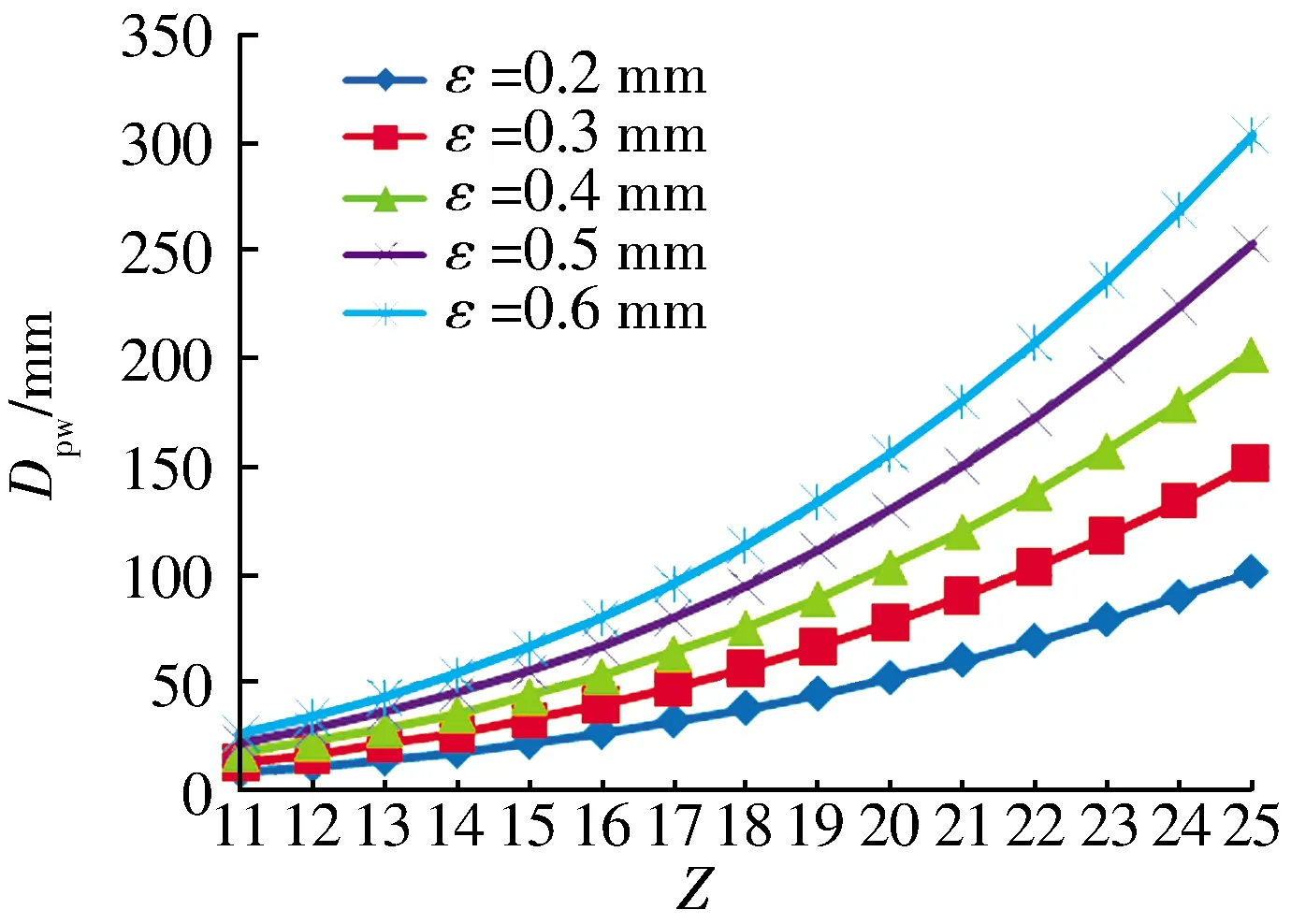
图3 一定锁量时无间隙排列滚子数与滚子组节圆直径的关系

表2 一定锁量时无间隙排列滚子数与滚子组节圆直径
3 实例计算
以某轴承为例,轴承外形尺寸为φ120 mm×φ160 mm×30 mm。若设定滚子直径为11 mm,滚子组节圆直径等于截面中心直径约为140 mm,由(3)式可得无间隙排列滚子数为40。假设该轴承滚子最大锁量要大于0.5 mm,由(7)式计算可得与之对应的滚子数需小于14.7,不满足要求,说明设定的主参数不能满足满装自锁设计的必要条件。
可知滚子组节圆直径在129.8~155.8 mm内变动时(实际滚子组节圆直径调整小于此范围),假设滚子组最大锁量大于0.5 mm,滚子数为20,由表1可得滚子直径应大于20.306 mm,对于实例中轴承截面尺寸,是不可能的,故此外形尺寸无法满足最大锁量大于0.5 mm的要求。
4 结束语
提出的滚子数、滚子直径、滚子组节圆直径的约束条件可以作为满装圆柱滚子轴承自锁的必要条件。通过计算获得了一定锁量下满装圆柱滚子轴承滚子直径与个数的关系图表和滚子直径与滚子组节圆直径的关系图表,可以快速判断能否满足自锁的必要条件,为满装自锁轴承的设计提供参考。
