斜面兜孔圆柱滚子轴承保持架稳定性分析
2021-07-22邓增辉刘延斌桑得雨
邓增辉,刘延斌,桑得雨
(河南科技大学 机电工程学院,河南 洛阳 471003)
高速圆柱滚子轴承是航空发动机的关键部件,保持架在高速运动过程中易发生振动,其性能会直接影响发动机的使用寿命和工作性能。据统计,在发动机故障引起的飞行事故中,有27%的故障是由轴承失效引起[1],保持架运行不稳定是引起轴承故障的重要原因,故有必要对保持架稳定性进行分析。
国内外学者对保持架稳定性做了大量研究:文献[2]发现高速运转时轴承保持架运行不稳定;文献[3]指出在高速运转时轴承零件的速度、惯性力对保持架动态特性影响较大,并建立轴承动力学微分方程,分析了保持架动态特性,结果表明高速状态有利于保持架的稳定;文献[4]建立了圆柱滚子轴承动态模型,分析了结构参数对保持架稳定性的影响,发现间隙比(兜孔间隙与引导间隙的比值)对保持架稳定性影响显著;文献[5]考虑轴承各零件之间的相互作用,尤其是保持架与内外圈滚道之间的相互作用,建立了油润滑圆柱滚子轴承保持架动力学模型,分析了间隙比、载荷、转速对保持架涡动的影响,在高速、轻载工况下,保持架稳定性好,间隙比大于1时,保持架稳定性变差;文献[6]建立了动力学分析模型,并开发了轴承动力学分析软件ADORE,分析结构参数及工况参数等对保持架稳定性的影响,结果与文献[5]一致;文献[7]分析了引导方式对保持架稳定性的影响;文献[8]分析了在高速、轻载工况下保持架复杂的受力状态,基于四阶龙格-库塔法分析了保持架质心轨迹,结果表明径向游隙和引导间隙过大或过小均会造成保持架不稳定;文献[9]采用精细积分和预估-校正相结合的算法对建立的圆柱滚子轴承动力学微分方程进行求解,分析了间隙比对保持架质心轨迹的影响,与文献[4]研究结果一致;文献[10]建立三自由度保持架动力学分析模型,分析了碰撞力、惯性力等对保持架质心轨迹及运动稳定性的影响,结果表明碰撞力、惯性力对保持架稳定性影响较大。
上述文献对保持架稳定性做了大量研究,但很少涉及斜面兜孔保持架的研究。鉴于此,以某斜面兜孔保持架圆柱滚子轴承为研究对象,考虑零件之间的约束、接触等条件,基于多体动力学软件ADAMS对轴承进行动力学仿真,分析转速、径向载荷及间隙比对保持架稳定性的影响。
1 斜面兜孔保持架圆柱滚子轴承
斜面兜孔保持架圆柱滚子轴承结构示意图如图1所示,保持架采用外圈引导。保持架兜孔结构[11]如图2所示,α,β分别为兜孔前、后壁倾角。以某型斜面兜孔保持架圆柱滚子轴承为研究对象,其主要结构参数见表1,内外圈及滚子材料均为GCr15,保持架材料为铜,材料参数见表2。假设轴承外圈固定,内圈旋转。

表1 斜面兜孔保持架圆柱滚子轴承主要结构参数Tab.1 Main structural parameters of cylindrical roller bearings with inclined cage pocket

表2 斜面兜孔保持架圆柱滚子轴承材料参数Tab.2 Material parameters of cylindrical roller bearing with inclined cage pocket

图1 斜面兜孔保持架圆柱滚子轴承结构示意图Fig.1 Structure diagram of cylindrical roller bearing with inclined cage pocket

图2 保持架结构示意图Fig.2 Structure diagram of cage
2 动力学模型
基于SOLIDWORKS建立轴承三维模型,将其导入ADAMS中。在内圈质心施加与重力方向相同的载荷及逆时针方向的转速。外圈施加全约束,限制内圈轴向和径向方向的自由度,使其在xOy平面内旋转,限制保持架轴向移动和歪斜,保持架仅在xOy平面内旋转和平移,限制滚子轴向平移和歪斜,仅在xOy平面内公转和自转。轴承动力学分析模型如图3所示。

图3 斜面兜孔保持架圆柱滚子轴承动力学分析模型Fig.3 Dynamic analysis model of cylindrical roller bearing with inclined cage pocket
在多体动力学软件ADAMS中,采用Impact函数计算滚子与内外圈以及保持架之间的碰撞接触力,该函数用速度和位移定义接触力,适用于连续性接触和非连续性接触,Impact计算的碰撞力由弹性力和阻尼力两部分组成,定义为
(1)
式中:F为零件之间的接触力;k为刚度系数;q0为零件之间碰撞的初始距离;q为零件之间碰撞的实际距离;e为接触力指数,对于线接触,取10/9;cmax
为最大阻尼系数,一般取刚度的0.1%~1%;dq/dt为零件之间的相对运行速度;d为刺入深度(阻尼最大时,滚子侵入内外圈滚道的深度),取0.1 mm;ε()为阶跃函数。
ADAMS中定义的接触刚度指静态刚度,刚度系数可表示为
(2)
(3)
式中:E′为当量弹性模量;Lwe为滚子有效长度;E1,E2为材料弹性模量;ν1,ν2为材料泊松比。
当保持架与套圈接触时,法向接触力可根据赫兹接触理论计算,即
Fn=kδ10/9,
(4)
式中:δ为接触变形量。
在ADAMS中摩擦力的计算采用Coulomb模型,摩擦因数与相对平移速度有关[12],摩擦因数为
μv=
(5)
式中:μ1为动摩擦因数;μ2为静摩擦因数;v1为动摩擦滑动速度;v2为最大静摩擦滑动速度;sign(v),v参考文献[12]。
滚子与内、外圈的静摩擦因数为0.12,动摩擦因数为0.08;滚子与保持架的静摩擦因数为0.10,动摩擦因数为0.06[13]。
3 保持架稳定性分析
为更直观评价保持架稳定性,引入速度偏差比和盒维数分析。
3.1 速度偏差比
速度偏差比可表示为
(6)

速度偏差比越小,保持架质心涡动轨迹越规则,保持架稳定性越高;反之,保持架稳定性越差。
3.2 盒维数
3.2.1 盒维数定义
设F为Rn上任意非空的有界子集,Nδ(F)是直径最大为δ,可以覆盖F的集的最少个数,则F的上下盒维数分别定义为[14]
(7)
若这两个值相等,则称此值为F的计盒维数,记为
(8)
盒维数越小,保持架稳定性越高,反之,稳定性越低。
3.2.2 盒维数计算
基于MATLAB计算保持架质心轨迹的盒维数,步骤如下:
1)将像素大小为n×n的保持架质心轨迹图像进行灰度处理,然后将灰度图导入MATLAB进行二值化处理,生成一个二进制的数据文件;
2)用大小为l×l的正方形盒子去覆盖保持架质心轨迹图像,统计出含0元素(黑色像素点)所需盒子的总数,记为Nl;
3)改变盒子边长l,继续统计盒子总数;
4)在对数坐标平面内,将所得的各组盒子尺寸和盒子数以坐标(logl,logNl)的形式用最小二乘法拟合,输出拟合直线的斜率,取相反数即为所求盒维数。
4 仿真分析
轴承径向载荷为2 000 N,转速为20 000 r/min,间隙比为0.2时,通过仿真分析可得不同兜孔前、后壁倾角下保持架质心涡动速度偏差比和质心轨迹盒维数,结果见表3,α=10°,β=-10°时保持架质心涡动速度偏差比和质心轨迹盒维数值均最小,保持架稳定性最好。以优化轴承(α=10°,β=-10°)和普通轴承(α=0°,β=0°)为例进行对比,分析转速、间隙比、径向载荷对圆柱滚子轴承保持架稳定性的影响。
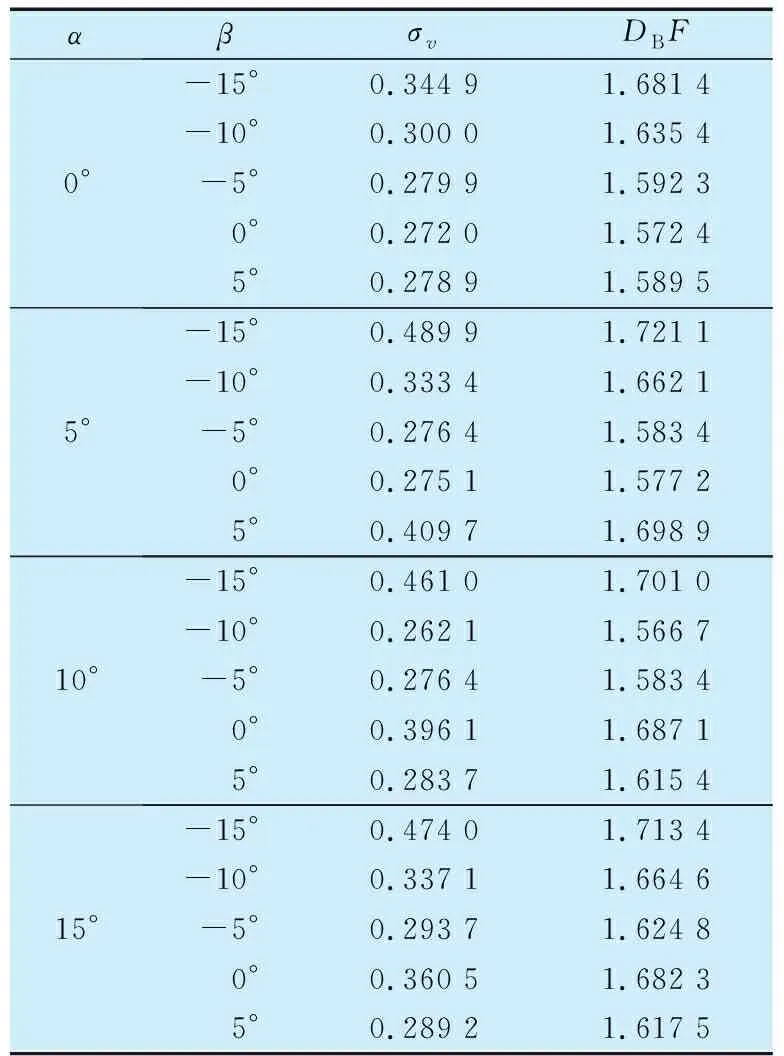
表3 保持架质心涡动速度偏差比和质心轨迹盒维数Tab.3 Deviation ratio of vortex velocity and box dimension of trajectory of cage center of mass
4.1 转速对保持架稳定性的影响
在径向载荷为2 000 N、间隙比为0.2时,保持架质心涡动速度偏差比和质心轨迹盒维数随转速的变化曲线如图4所示:1)优化轴承和普通轴承的质心涡动速度偏差比及质心轨迹盒维数均随转速增大逐渐减小,最终趋于稳定,说明保持架稳定性逐渐增强并趋于稳定;2)优化轴承的质心涡动速度偏差比和质心轨迹盒维数均小于普通轴承,表明优化轴承保持架稳定性更好。

图4 保持架质心涡动速度偏差比和质心轨迹盒维数随转速的变化曲线Fig.4 Variation curve of box dimension of deviation ratio of cage center and trajectory of cage center of mass with rotating speed
不同转速下优化轴承和普通轴承保持架质心轨迹分别如图5和图6所示,随转速增大,优化轴承和普通轴承保持架质心轨迹都逐渐趋于圆形,说明随转速增大,保持架逐渐趋于稳定涡动状态。

图5 不同转速下优化轴承保持架质心轨迹Fig.5 Trajectory of center of mass of optimized bearing cage under different rotating speeds
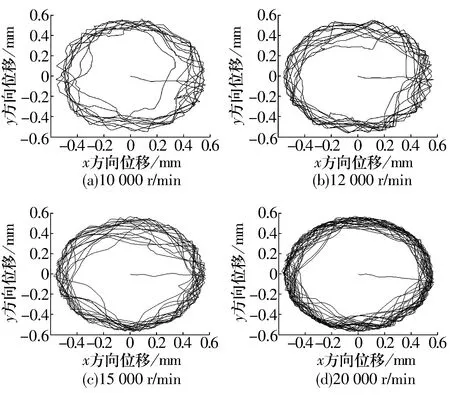
图6 不同转速下普通轴承保持架质心轨迹Fig.6 Trajectory of center of mass of ordinary bearing cage under different rotating speeds
综上可知,随转速增大,保持架稳定性逐渐提高,且优化轴承的质心涡动速度偏差比和质心轨迹盒维数均小于普通轴承,说明优化轴承稳定性优于普通轴承。
4.2 径向载荷对保持架稳定性的影响
在转速为20 000 r/min、间隙比为0.2时,保持架质心涡动速度偏差比和质心轨迹盒维数随径向载荷的变化曲线如图7所示,由图可知:随径向载荷增大,保持架质心涡动速度偏差比先减小后增大,说明保持架稳定性先增强后减弱,但两种轴承保持架稳定性区别不明显;随径向载荷增大,盒维数逐渐减小,保持架趋于越稳定。
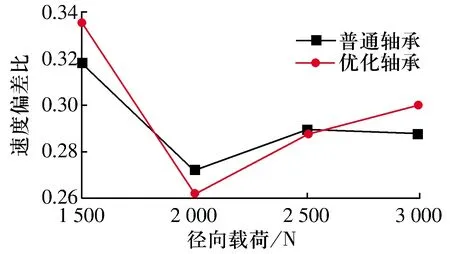

图7 保持架质心涡动速度偏差比和质心轨迹盒维数随径向载荷的变化曲线Fig.7 Variation curve of box dimension of vortex velocity of cage center and trajectory of cage center of mass with radial loads
不同径向载荷下优化轴承和普通轴承保持架质心轨迹分别如图8和图9所示,结合图7可知,优化轴承保持架稳定性优于普通轴承,当径向载荷为2 000 N时,优化轴承保持架稳定性最好。
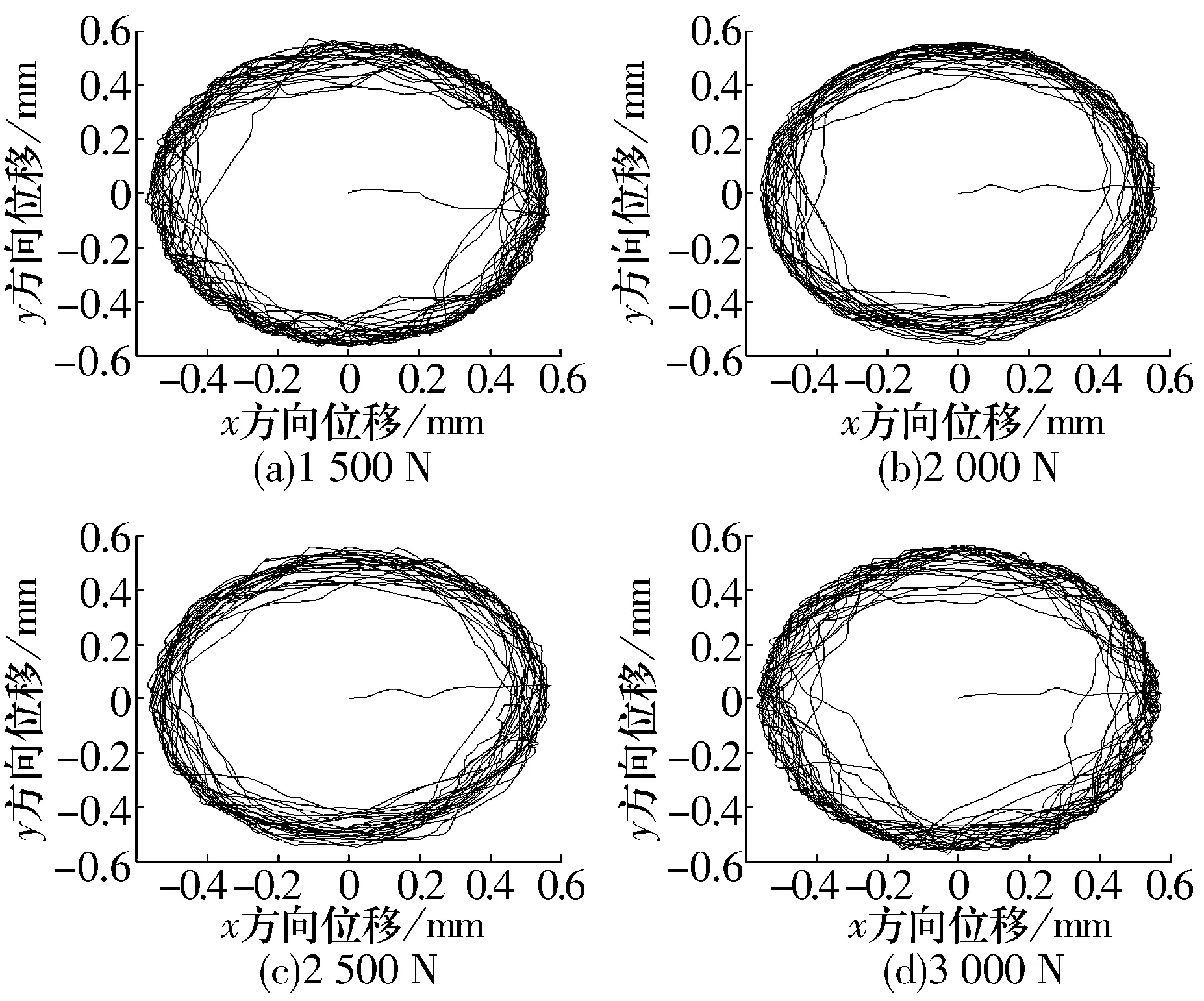
图8 不同径向载荷下优化轴承保持架质心轨迹Fig.8 Trajectory of center of mass of optimized bearing cage under different radial loads

图9 不同径向载荷下普通轴承保持架质心轨迹Fig.9 Trajectory of center of mass of ordinary bearing cage under different radial loads
4.3 间隙比对保持架稳定性的影响
在径向载荷为2 000 N、转速为20 000 r/min时,保持架质心涡动速度偏差比和质心轨迹盒维数随间隙比的变化曲线如图10所示,随间隙比增大,涡动速度偏差比和盒维数值均增大;间隙比小于0.6时,优化轴承和普通轴承的速度偏差比和盒维数值变化基本一致,且涡动状态稳定;间隙比大于0.6时,两种轴承保持架涡动速度偏差比和盒维数值都明显增大,开始处于不稳定的涡动状态,这是由于引导间隙减小,保持架与引导面之间的碰撞频率增加,使保持架运动处于不稳定状态。
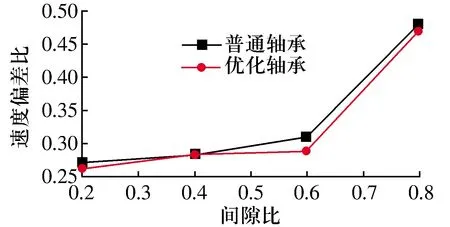
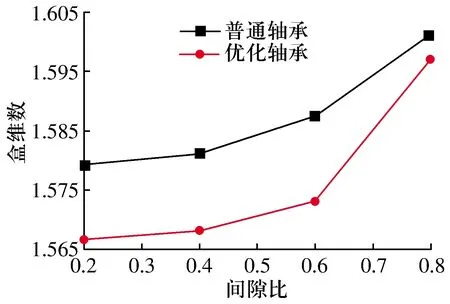
图10 保持架质心涡动速度偏差比和质心轨迹盒维数随间隙比的变化曲线Fig.10 Variation curve of box dimension of vortex velocity of cage center and trajectory of cage center of mass with clearance ratios
优化轴承和普通轴承保持架质心轨迹分别如图11、图12所示,随间隙比增大,保持架质心轨迹由规则的圆形逐渐变成不规则状态,混乱程度增大,保持架运动趋于不稳定。结合图10可知,优化轴承保持架稳定性优于普通轴承。

图11 不同间隙比下优化轴承保持架质心轨迹Fig.11 Trajectory of center of mass of optimized bearing cage under different clearance ratios
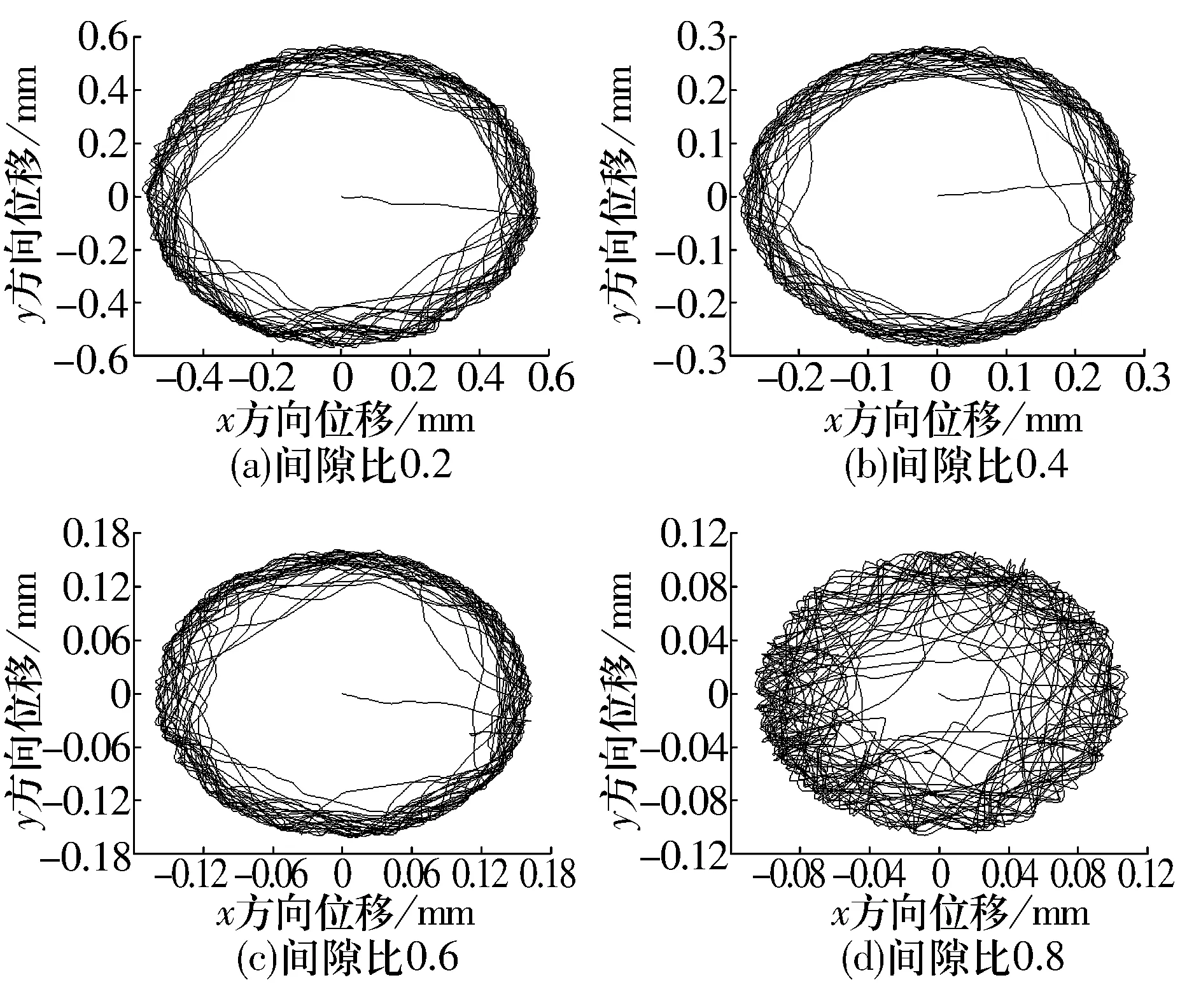
图12 不同间隙比下普通轴承保持架质心轨迹Fig.12 Trajectory of center of mass of ordinary bearing cage under different clearance ratios
5 结论
建立了斜面兜孔保持架圆柱滚子轴承多体动力学分析模型,分析了保持架兜孔倾角对轴承稳定性的影响,并对轴承进行优化,对比分析了转速、径向载荷、间隙比对优化前后轴承保持架稳定性的影响,得出如下结论:
1)兜孔前壁倾角α=10°、后壁倾角β=-10°时,保持架稳定性最好。
2)在10 000~20 000 r/min转速范围内时,优化轴承保持架稳定性明显优于普通轴承。超过20 000 r/min时,两种轴承保持架稳定性差别不大。
3)随径向载荷增大,优化轴承与普通轴承稳定性变化差别不大。
4)随间隙比增大,优化轴承和普通轴承保持架稳定性逐渐变差。间隙比小于0.6时,保持架处于稳定涡动状态;间隙比大于0.6时,保持架处于不稳定涡动状态。
