三峡地区岩质边坡滑动面裂隙水力劈裂分析

2021-07-22邹前堡

东北水利水电 2021年7期

邹前堡

（赣州市水兴建设有限公司，江西赣州341000）

0 引言

我国的滑坡灾害具有分布广、危害大等特点，每年由于滑坡灾害造成的损失不计其数[1]。其中，岩质滑坡由于其规模较大、滑坡速度快等性质，造成的危害是最为严重的。因此，对岩质边坡滑坡启动机理的研究对边坡治理工程具有重要意义。陈喜昌等[2]通过对大量滑坡实例的调查研究，最终得出了降雨后地下水位的升高是导致岩质边坡产生滑坡的重要因素。周永利等[3]对含裂隙的岩质边坡失稳机制进行研究，认为岩质边坡失稳与后缘裂隙的水头高度、水致弱化函数等相关。曾芮等[4]模拟了降雨对岩质边坡的变形破坏机理，认为雨水在岩体裂隙中快速充水，对岩体产生向外的推力是导致岩体崩塌的直接诱因。

岩质边坡产生滑坡不仅要满足力学失稳条件，在一定的水力条件下有对应的软弱结构，还需具有外倾软弱破裂面。而破裂面的形成与边坡裂隙、水力条件等因素相关，当雨水渗入裂隙时，造成裂隙内的水压力升高，导致裂隙继续扩张甚至贯通，岩质边坡渗透性增加，渗流速度加快，促使形成新软弱破裂面，如此循环，最终导致边坡岩体发生破坏，使得滑坡容易产生。由此可知，岩质边坡滑坡的形成与雨水渗入裂隙中产生的水力劈裂效应相关。鉴于此，本文根据断裂力学理论，研究岩质边坡滑动面水力劈裂作用，并推导岩质边坡的临界水头公式。

1 力学模型的建立

根据Hoek 和Bray 给出的典型岩质边坡横坡面图，绘制滑动面的水力模型，见图1。并假定该边坡发生破裂的滑动面倾角小于坡角，该滑动面为一平面。滑动面后缘的张裂缝与水平方向垂直，走向与该边坡走向一致。降雨后，雨水可沿着张裂缝渗透至滑动面。

岩质边坡内的岩体含有大量的裂纹，取图1 中距滑动面顶端为h的岩体内裂纹为分析对象。假定岩体为脆弹性材料，裂纹失稳扩展时的应力满足断裂力学条件。将岩体内的三维裂纹简化为含闭合单裂纹的二维平面，见图2。

图1 岩质边坡结构面力学模型

图2 含单裂纹岩体的力学模型

一般情况下，发生岩质滑坡时的深度不会特别大，构造应力作用较小，因此，仅考虑自重应力的作用。则图2 中的垂直应力σv和水平应力σh的计算公式：

式中：γ为边坡岩体的重度，kN/m3；h为岩体的厚度，m；k0为岩体的侧压力系数，一般情况下小于1。

图2 中，闭合单裂纹的长度为2a，α为单裂纹中轴线与垂直应力σv作用方向之间的夹角（裂纹方位角）。闭合单裂纹内作用有孔隙水压力p，假设孔隙水压力沿裂纹各个方向的作用力是相同的，则根据图2 中的应力状态，可得到裂纹面上的正应力σα和剪应力τα：

2 结构面水力劈裂分析

由于在断裂力学中规定受拉为正，受压为负，因此需在式（2）前面添加负号。由式（2）可知，单裂纹面上既有正应力σα作用，也有剪应力τα作用，由此可把裂纹失稳扩展的模式当成Ⅰ-Ⅱ复合型模式。即当裂纹面上的正应力为拉应力时（σα>0），裂纹的失稳扩展模式为压剪复合型；当裂纹面上的正应力为压应力时（σα<0），裂纹的失稳扩展模式为拉剪复合型。

当σα> 0 时，此时裂纹扩展模式属于拉剪复合型。根据工程近似断裂准则[5]，得到裂纹失稳扩展的判别表达式：

式中：KⅠc为Ⅰ型断裂韧度；KⅠ为Ⅰ型应力强度因子；KⅡ为Ⅱ型应力强度因子，其表达式分别为：

式中：a为闭合单裂纹的半长，m。

将式（2）代入式（4），得到的结果再代入式（3），即可得到：

将式（5）进行移项处理，则可得到边坡滑动面岩体在拉剪状态时的临界水压力：

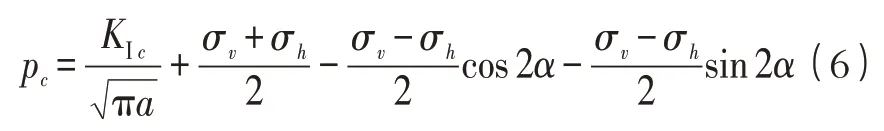
将式（1）代入式（6），则式（6）中的临界水压力可表示为：

当σα<0 时，此时裂纹扩展模式属于压剪复合型。在工程中常把这类情况近似看成纯Ⅱ型裂纹的断裂问题，此时取Ⅰ型应力强度因子KⅠ=0。在足够大的压力作用下，裂纹面会逐渐闭合并发生相对滑动，裂纹面间会产生摩擦力σαtanφ和粘聚力c，则裂纹面间的有效剪应力τe可表示为：

式中：φ为裂纹面的内摩擦角。由断裂力学中Ⅱ型裂纹破坏判据可知：

式中：KⅡc为Ⅱ型断裂韧度。

将式（2）、式（8）及式（9）进行联立，则可得到边坡滑动面岩体在压剪状态时的临界水压力：

将式（1）代入式（10），则式（10）中的临界水压力可表示为：

当岩体内存在多条成周期分布的等长、等间距的平行共线裂纹如图3 所示。

图3 岩体内周期分布的共线裂纹

将单裂纹条件下的断裂韧度代入式（12），则可得到：

将式（13）分别代入式（7）和式（11），得到共线裂纹发生拉剪破坏时的临界水压力p′c为：

当雨水渗入边坡滑动面顶端的张裂缝时，假定在周围产生的孔隙水压力恰好在h1处（图1）达到临界水压力pc，此时裂缝开裂，则有：

式中：γw为水的容重，kN/m3。

将式（16）分别代入式（14）和式（15）得到拉剪破坏时的临界水头：

式（17）中除了α角未知以外，其余均为已知值，则在同一临界水头条件下最容易发生水力劈裂现象的裂纹方位角为：

压剪破坏时的临界水头为：

同理，在同一临界水头条件下最容易发生水力劈裂现象的裂纹方位角为：

假如滑坡体为图1 所示，根据几何关系可得：

式中：H为坡体高度；h0为滑动面顶端张裂缝的高度；h1为临界水头。假设滑坡体厚度是均匀的，则h为常数。水头超过临界水头h1时会发生水力劈裂。

3 案例分析

以文献［7］三峡地区的金铜村滑坡为例，该滑坡厚度差别不大，可按均布边坡计算，重度约为22 kN/m3，厚度h约为15 m，滑坡体总长度约为260 m，滑动面顶端后缘的张裂缝长度h0约为12 m，滑坡体高度H约为 54.9 m，φ=22.5°，c=12 kPa，取k0=0.5。根据文献［8］，取KⅠc=0.8 MPa/m0.5，KⅡc=0.71 MPa/m0.5。

根据以上数据，代入式（17），取α=22.5°，得到裂纹发生拉剪型破坏时的不同裂纹连通率下的临界水头。

由式（22）可知，在同一裂纹长度下，发生拉剪破坏时的临界水头随着连通率的增加而增加。此外，式（22）中的临界水头h′1恒大于h0，所以该边坡结构面不会发生水力劈裂现象。

将数据代入式（19），取α=45°+φ/2，得到裂纹发生压剪型破坏时的不同裂纹连通率下的临界水头。

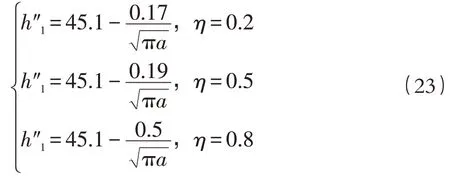
由式（23）可知，在同一裂纹长度下，发生压剪破坏时的临界水头随着连通率的增加而减小。在该破坏模式下，边坡结构面会有一定几率发生水力劈裂。当η=0.2 时，发生水力劈裂时的最大裂纹半长为8.39 × 10-6m；当η=0.5 时，发生水力劈裂时的最大裂纹半长为1.05×10-5m；当η=0.95 时，发生水力劈裂时的最大裂纹半长为7.26×10-5m。