基于EEMD和HHT的低压异步电动机故障诊断

汤 成，张 懿，魏海峰，周啸伟，丁 伟

(1.江苏科技大学 电子信息学院，镇江 212003；2.常熟瑞特电气股份有限公司，常熟 215500；3.大全集团有限公司，镇江 212200)

0 引 言

在船舶行业中，船舶上的设备运作几乎都需要通过电机来实现。电机是电能和机械能相互转化的一种设备，低压异步电动机是目前应用最广的机电传动装置，有着功率容量大、性能稳定、制造成本低、适应性强等优点。然而，船舶上的中小型电动机数量多、位置分散、安装环境各异、起动方式多样、无法进行全生命周期的全过程监测。随着长时间的运作，电机各个部件的可靠性降低，出现故障的概率升高，电动机的性能下降、磨损加剧，甚至最终发生灾难性故障，造成严重的人力物力损失。电机状态监测及故障诊断技术提供了一种“治未病”的方法，应用各种信号分析与处理技术对取得的电机参数进行分析，在此基础上提取出对特定故障敏感的特征信息，在电机出现小型故障时发现并准确定位故障，避免灾难性故障的发生。

近年来，针对使用振动传感器进行电机故障诊断，国内外学者进行了深入研究。目前，较为常用的特征提取方法是快速傅里叶变换(以下简称FFT)和短时傅里叶变换(以下简称STFT)。文献[1]对FFT分析具体故障进行了实际工业应用。FFT就是将信号变换到频域，是快速计算离散傅里叶变换(DFT)的计算机算法，在频域上对时域上的信号进行描述，具有降低计算复杂度、减少计算时间的特点。但FFT对于时间不敏感，不能对时间域上的信号的某一局部进行刻画，对突变和非平稳信号的描述效果也不理想。为了解决这些问题，利用STFT进行信号处理[2]，它在FFT的基础上增加了窗函数，利用窗函数对信号进行截取，这样就可以描述不同时刻的频谱，便于非平稳信号的处理。然而，它的窗函数不能随信号频率的变化而变化，往往会出现频率分辨率差或时间分辨率差的现象。因此，使用小波变换的方式对信号进行分析。小波变换对傅里叶变换的基底进行变换，把基函数由正弦信号变为长度有限、会衰减的小波基(一般是两个正交基的分解)[3]，克服了STFT窗函数不能随频率变化的缺点。文献[4]利用小波变换进行感应电动机转子偏心故障诊断，证明了可以同时观察频率和时间轴，达到时间和频率的最优化。但是，小波变换在处理信号和噪声频带混叠的情况下效果不理想。Norden Huang提出了经验模态分解(以下简称EMD)方法，它是一种针对非平稳信号的信号处理方法，这种方法将原始信号分解成一系列具有时变频率的基本模态函数，能够反映出非平稳信号的局部特征，无需预先选择基函数，直接进行分解，对不同的特征尺度具有自适应性，适合非线性非平稳信号的分解[5-6]。然而，EMD存在模态混叠问题[7]。Flandrin又解决了EMD分解出现的模态混叠现象，提出了集合经验模态分解。集合经验模态分解的方法运用白噪声在任何频率上分布均匀的特征把白噪声加入EMD分解中，有效解决了模态混叠现象，但是在引入噪声后出现了不确定性[8]。

本文旨在利用集合经验模态分解和希尔伯特-黄变换对低压异步电动机的振动信号进行分析，对电机常见故障进行分析。利用压电式振动传感器采集电机运行时的振动信号，采集到的信号将采用集合经验模态分解(以下简称EEMD)的方法进行分解，利用相关系数提取出关联性较大的分量，对振动信号进行重构，重构后的信号使用希尔伯特-黄变换(以下简称HHT)信号处理方法，进行故障的判断。这样，既能解决EMD留下的模态混叠现象，又可以利用相关系数进行筛选，将低相关系数甚至负相关系数的分量进行去除，解决引入噪声后的不确定性。

1 振动信号的采集

根据2015年中国船级社发布的《智能船舶规范》[9]，智能故障诊断技术中应注重以下几个方面：

1)故障诊断思维的延申。要从通过故障现象分析故障机理、通过经验解决问题，转向以经验机理为基础、故障现象为表征、监测数据为内核、智能算法为手段、故障预测和状态监测为目的的新方向。

2)诊断目标的延申。从传统的故障之后分析解决问题，转向及时识别机械故障的出现和演变、实时监测系统运行状态、提前预测并化解、减少或避免事故的新方向。

3)诊断方法的延申。从人工搜集并筛选数据、基于机理提取故障特征的切片式诊断方法，转向多工况、多随机因素干扰下利用智能算法提取、筛选数据特征，并进行故障数据解析和全局分析的新方向。

振动信号采集是利用振动信号进行电机故障诊断的基础。要想达到《智能船舶规范》中的要求，必须选择一款适合进行数据特征提取、筛选的，精度较高的振动传感器。常见的振动传感器包括速度振动传感器、加速度振动传感器和涡流振动传感器，如表1所示。

表1 振动传感器分类及特点

从表1中可以看出，加速度振动传感器是唯一适合于测量中高频旋转机械的振动传感器。加速度振动传感器不仅具有适合测量电机振动的特点，同时还具有结构紧密、体积小，安装方式多样等特点，并且可以利用其频谱比较广的特点，在整个频谱范围内进行频谱分析，以便及时发现微小的故障。因此，相比于表1中的其他两种传感器，采用加速度传感器测量异步电动机有着速度快、精度高、兼容性佳、针对性强的独到优势，可以实时监测不同频率下振动信号的信号振幅，以满足《智能船舶规范》智能故障诊断技术中要求的数据的实时性和准确性。

加速度振动传感器可分为磁电式和压电式两种。压电式加速度振动传感器具有1 Hz～9 000 Hz的宽大频率测量范围，并具有更廉价、更耐用等优势。此外，由于船舶上中小型电动机位置分散,安装环境各异，而压电式加速度振动传感器安装方式多样，可以采用金属螺栓安装、对地绝缘转换螺栓连接、胶粘剂粘接和磁铁转换吸盘连接四种安装方式。因此，船用振动信号采集使用压电式加速度振动传感器。实验平台选用CA5005 M10型压电式加速度振动传感器，传感器参数如表2所示。

表2 振动传感器参数表

在实验环境搭建时，将实验用风机(三相低压异步电动机)用四只螺柱进行固定，在风机轴承正上方安装压电式加速度振动传感器，安装采用胶粘剂粘接加磁铁转换吸盘连接双重固定方式，以保证安装牢固，不会掉落或影响安装刚度。

综上，实验平台采用压电式加速度振动传感器，利用风机作为低压异步电动机进行实验，风机及振动传感器安装位置如图1所示。

图1 振动信号故障诊断实验平台

平台使用的风机为低压异步电动机，外接三相交流电压380 V电源，电机参数如表3所示。

表3 低压异步电机参数

2 振动信号的处理

压电式加速度传感器采集到的信号，需要通过特征提取，才能进行故障识别和预测。利用合理的手段进行振动信号的故障特征提取，是系统故障诊断中的重要一环，信号的提取既保证了将振动信号中的有用信息准确提取，又可以明确机械故障信息表征。目前,对于振动信号的处理通常采用的都是FFT或STFT，虽然STFT在FFT的基础上增加了取样的窗函数，但是两者对于非平稳信号的处理都不甚理想。使用EEMD可以对不同特征尺度的信号进行自适应，更适合于非线性非平稳信号的分解。

2.1 EEMD

EMD是一种新型、自适应时频局部的时频分析法，不仅能够处理非静态过程，还能使用按初始数据确定的自适应变换基的变换[10]。EEMD是一种噪声辅助的数据分析手段，从EMD发展而来并解决了EMD发生的模态混叠现象。下面从EMD开始对EEMD的原理及特性进行分析。

对于非平稳信号x(t)而言，每一时刻的频率都随时间变化，不能用傅里叶变换中的全局性概念进行分析，需要采用瞬时频率来表示信号的瞬时特性。采用希尔伯特变换可以将给定非平稳信号x(t)变换为y(t)：

构造解析函数z(t)：

把瞬时相位进行微分，得到瞬时频率：

EEMD是在EMD的基础上加入白噪声，并使用EMD算法进行分解，可以得到本征模态函数(以下简称IMF)。根据白噪声具有统一的频率分布，将白噪声添加进原信号中，因为白噪声不同，因此在获得IMF分量时相邻IMF分量不会产生关联，即EEMD解决了EMD的模态混叠现象。

假设任何复杂信号都是多个固有模态函数的和，任何模态函数都可以在线性和非线性之间相互独立，则非平稳信号x(t)的EEMD分解步骤如图2所示。

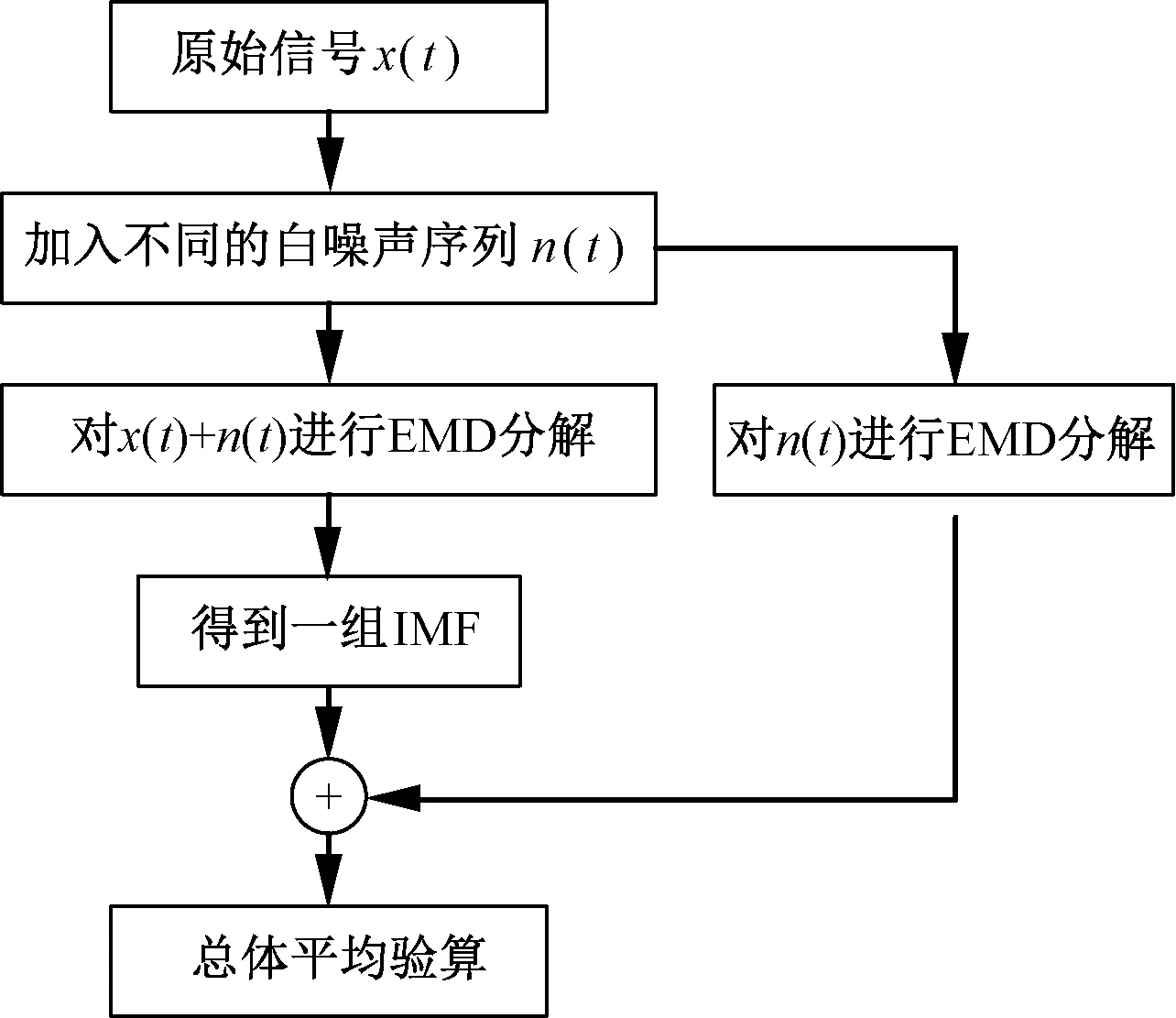
图2 EEMD分解流程图

2.2 相关系数

在得到各级IMF分量后，可以利用相关系数的方法对IMF分量进行筛选。相关系数是两个变量之间的线性关系度量，在本文中，各级IMF分量的相关系数是指各级IMF分量和原信号之间的线性关系大小。相关系数的公式：

式中：x(t)表示原信号，yi表示第i级的IMF分量。利用x(t)和yi(t)的相关系数可以得到EEMD分解结果与原信号之间的线性相关性。根据公式可知，在原信号和IMF分量呈现负相关时，相关系数的值为负，且线性相关性越高，相关系数的值越大。在相关系数Q<0或低于设定阈值时，IMF分量是原信号的伪分量。这样，就可以利用相关系数解决EEMD引入噪声后IMF分量的不确定性。

2.3 HHT变换

在剔除伪IMF分量后,对IMF分量进行重构，重构步骤和EMD分解相反。接着，对重构后的信号进行HHT变换，得到重构信号的包络。定义重构信号为H(ω)，则边际谱函数h(ω)：

边际谱函数H(ω)提供了每个频率上的总振幅，即反映了在每个频率上振动的情况，是对整个数据跨度的振幅的累积。

3 电动机故障诊断

电动机故障诊断实验流程如图3所示，实验通过对风机振动信号的采集、数据处理，最终得到电机的故障诊断结果。

图3 电机故障诊断模型

根据图3的过程，利用MATLAB对采集到的数据进行信号处理，数据由每组3 304个分布在不同频率上采集点所构成，上传的数据采样间隔为3 s。利用20组数据对近60 s电动机的振动状态进行描述。下面列举出异步低压电动机在正常、堵转、三相不平衡三种状态下对采集到的数据进行信号处理的结果。

3.1 正常状态下的EEMD分析

在正常情况下起动风机，采集风机的振动信号，通过EEMD，得到各级IMF分量，即IMF1～IMF12，各级IMF分量如图4所示。

图4 正常状态下振动信号EEMD分解结果

在电机运行过程中，振动量值的采集往往同时包含着噪声等无关分量，因此在EEMD分解后的各级IMF分量中包含着无关分量，甚至负相关分量，称为伪分量。可利用各级分量的相关系数，将IMF分量中相关系数Q>10-4的分量进行提取，并定义提出伪分量后的分量为IMF’，各级IMF’分量如图5所示。在IMF’分量中，每个分量与原信号都保持着较高的相关系数。

图5 正常状态下利用相关系数提取IMF分量结果

对经过筛选后的IMF分量,IMF’分量进行重构，得到重构后的信号，经重构的振动信号如图6所示。

图6 正常状态下的信号重构

利用HHT，得到重构信号的包络，如图7所示。

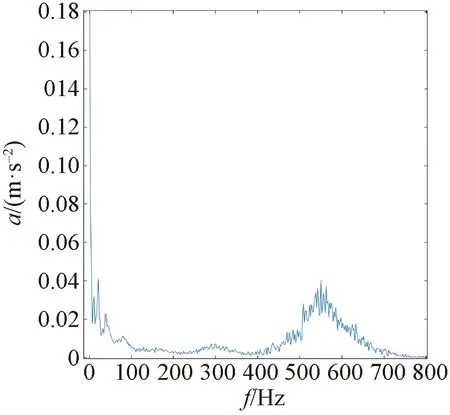
图7 正常状态下的边际谱函数

经过观察正常状态下的幅频曲线可以看出，在正常状态下，在频率极小时，取到的幅值>0.18 m/s2；在频率为300 Hz时，幅值有一次明显的提升；在频率略高于550 Hz时，幅值达到第二次高峰，取到的幅值略大于0.04 m/s2。

3.2 堵转状态下的EEMD分析

在风机成功起动后，将风机出风口用重物封住，使气流无法从出风口排出风机。对于风机，这种措施可以造成轻微的堵转故障。将风机开启后堵住出风口，将采集到的振动信号通过EEMD，得到各级IMF分量，即IMF1～IMF12，IMF分量如图8所示。

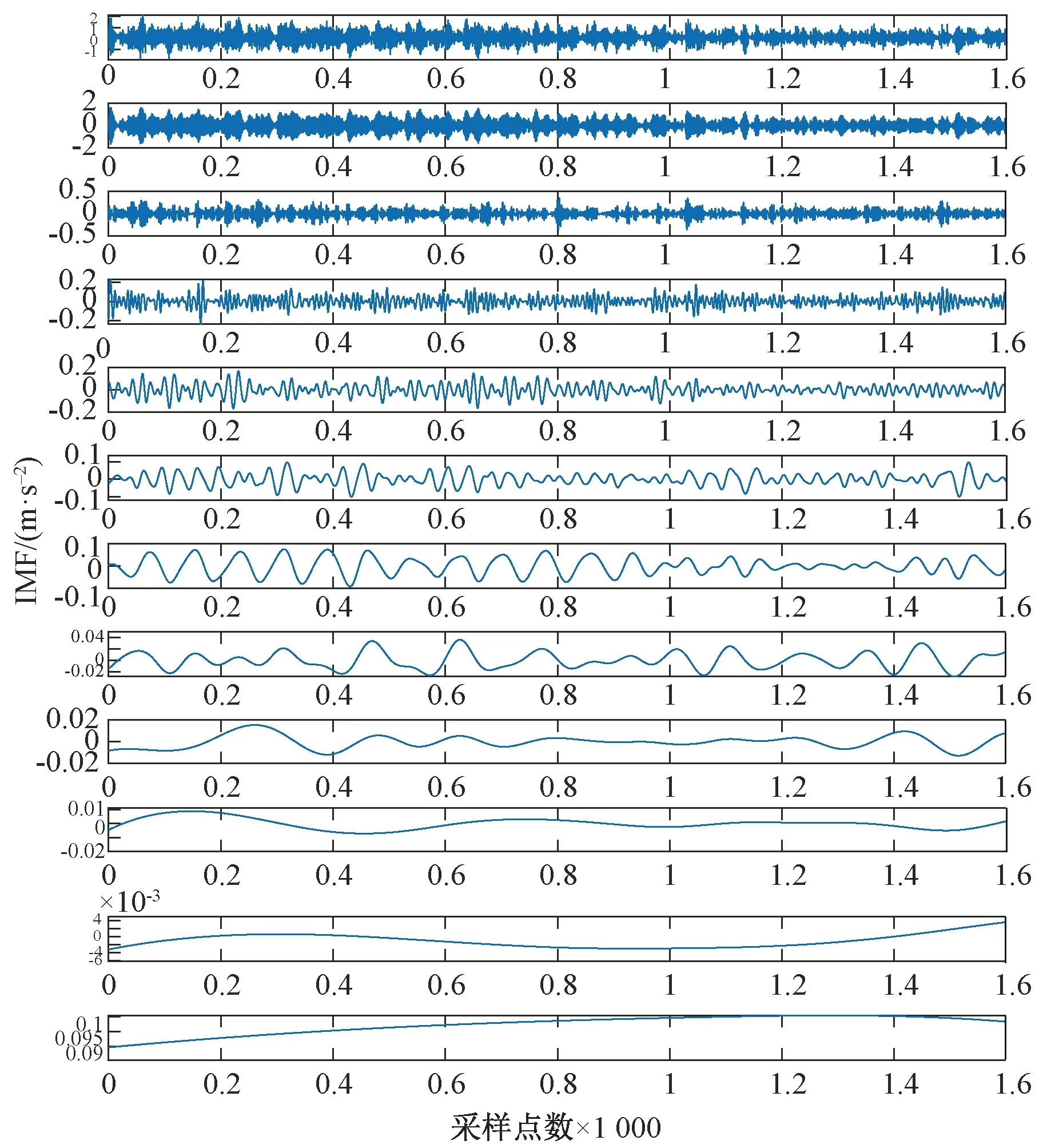
图8 堵转状态下振动信号EEMD分解结果

堵转时，将IMF分量相关系数Q>10-4的分量进行提取，并定义新的经过筛选后的分量为IMF’，各级经过筛选后的IMF’分量如图9所示。

图9 堵转状态下利用相关系数提取IMF分量结果

在堵转情况下，对经过筛选后的IMF分量，IMF’分量进行重构，得到堵转情况下重构后的信号，经重构的振动信号如图10所示。

图10 堵转状态下的信号重构

利用HHT，得到重构信号的边际谱函数，如图11所示。

图11 堵转状态下的边际谱函数

可以看出，在堵转情况下，和正常状态下相比，在频率极小时，取到的幅值约为0.12 m/s2，远小于正常情况下的0.18 m/s2以上；在频率为300 Hz时，幅值有一次明显的提升，与正常状态下相同；在频率略高于550 Hz时，幅值未超过频率为25 Hz左右的极大值，取到的幅值小于0.04 m/s2。

3.3 三相不平衡状态下EEMD分析

将一个螺栓固定在风机的铁片上，人为制造一个三相不平衡故障。开启风机，采集到的振动信号通过EEMD，得到各级IMF分量，即IMF1～IMF12，IMF分量如图12所示。

图12 三相不平衡状态下振动信号EEMD分解结果

发生三相不平衡故障时，将提取到的IMF分量相关系数Q>10-4的分量进行提取，并定义去除伪分量的各级本征模态函数为IMF’，各级经过筛选后的IMF’分量如图13所示。

图13 三相不平衡状态下利用相关系数提取IMF分量结果

在三相不平衡情况下，对经过筛选后的IMF分量,IMF’分量进行重构，得到堵转情况下重构后的信号，经重构的振动信号如图14所示。

图14 三相不平衡状态下的信号重构

利用HHT，得到重构信号的边际谱函数，如图15所示。

图15 三相不平衡状态下的边际谱函数

可以看出，在三相不平衡状态下，和正常状态下相比，在频率极小时，取到的幅值略大于0.14 m/s2，小于正常情况下的0.18 m/s2以上；在频率为250 Hz时，幅值有一次明显的提升，比正常状态下相同下早了50 Hz左右；在频率略高于550 Hz时，幅值未超过频率为25 Hz左右的极大值，取到的幅值小于0.04 m/s2。

3.4 重复实验

按照故障诊断模型的方法，对上述三种状态进行其余87次实验，得到了全部90组数据的诊断结果，其中有88次诊断结果和人为设置的故障相一致，其余2次正常情况被认作堵转，诊断正确率为97.7%。

4 结 语

利用振动信号，进行EEMD、相关系数提取、重构信号和HHT得到信号的包络，利用包络进行故障诊断，并通过实例对此方法进行了验证。结果证明，EEMD对于非平稳信号的分解有着很好的作用，HHT所得的边际谱函数也可以对异步电动机的常见故障进行准确的识别。此种方法仅仅通过一个压电式加速度振动传感器，使用磁铁转换吸盘加胶粘安装，诊断结果明了、准确，在至多60 s的时间内就能发现轻微的电机常见故障，在实际船舶行业分布式电机的实时监测和故障诊断中具有较高的使用价值和经济价值。