基于精确有限元模型的弧齿锥齿轮承载振动特性分析

2021-07-22刘孝柏曹艳玲曹雪梅

河南科技大学学报(自然科学版) 2021年6期

刘孝柏, 曹艳玲, 曹雪梅

(河南科技大学 a. 机电工程学院；b.车辆与交通工程学院，河南洛阳 471003)

0 引言

弧齿锥齿轮传动平稳，承载能力大，广泛应用于汽车、轮船和航空航天等领域，用于传递两轴之间的运动和动力。在齿轮啮合传动过程中，承载传动误差作为振动的直接激励，是产生振动和噪声的主要因素[1-3]，对整个传动系统的平稳性影响很大。因此，分析弧齿锥齿轮的承载振动特性，对提高齿轮传动平稳性具有重要意义。

文献[4-5]基于局部综合法和遗传算法，对准双曲面齿轮的加工参数进行优化设计，进而有效地提高了齿轮副的动态特性。文献[6]利用ease-of差齿面，结合轮齿刚度解析法，提出轮齿时变啮合刚度算法与承载分析方法，对斜齿轮的动态啮合性能进行了分析。文献[7]在计算时变啮合刚度的基础上，推导了承载传动误差简化计算公式，分析了齿面印痕和几何传动误差对承载传动误差的影响。文献[8]提出了几何传动误差曲线幅值的设计，结合承载传动误差，使齿轮在不同载荷条件下既能具有高重合度，又保证了相对低的误差敏感性，有效改善了齿轮的动态特性。文献[9]研究了不同载荷下，接触椭圆长轴长度、接触迹线方向对时变啮合刚度和传动误差的影响规律。文献[10-11]采用有限元方法对螺旋锥齿轮进行了接触分析，讨论了齿轮接触刚度计算方法、应力变化和振动冲击等。

弧齿锥齿轮有限元模型通常是利用编程软件生成单齿凸面和凹面的齿面点，然后导入CAD软件生成全齿三维模型，通过手动调整主从动轮的装配位置来模拟滚检，很可能产生装配误差和轮齿干涉现象[12]。CAD装配模型通过CAE软件中的实体切分、网格划分等操作生成有限元模型，不仅工作量大，还导致齿面的精度损失，齿面拓扑形状微米量级的变化就能对齿轮啮合性能产生较大的影响[13-14]，因此，基于CAD软件建立的齿轮副有限元模型难以满足高精度建模的要求。

本文根据加工参数计算齿面点，直接以齿面点为网格节点，建立高精度的轮齿有限元模型。采用轮齿接触分析，精准计算大小轮齿面啮合位置，从而建立精确的齿轮副有限元装配模型。

采用静态分析方法计算轮齿的齿面接触应力、接触印痕及不同负载下的承载传动误差曲线，并将承载传动误差作为激励，研究了弧齿锥齿轮副承载振动特性，为提升齿轮副承载动态特性奠定基础。

1 弧齿锥齿轮有限元分析前处理

1.1 有限元模型的建立

根据弧齿锥齿轮的基本参数和机床加工参数求解大轮齿面方程，建立大轮的旋转投影平面[15]。图1为大轮网格节点在旋转投影面上的位置分布。

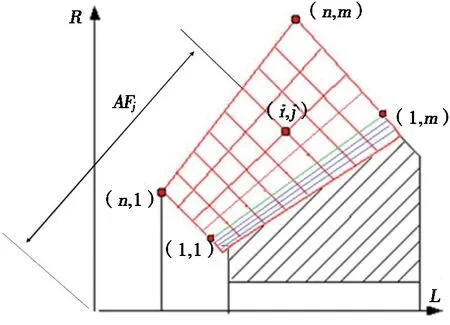
图1 大轮网格节点在旋转投影面上的位置分布

齿面上每一个节点坐标都满足：

(1)

其中：L为旋转投影面的横坐标轴；R为旋转投影面的纵坐标轴；m为沿齿长方向划分的网格节点个数；n为沿齿高方向划分的网格节点个数；u和v为齿面方程的两个变量。

齿轮的承载传动是高度复杂的几何非线性和边界条件非线性的接触问题，齿面不可避免地会受到冲击甚至产生扭曲变形，由于六面体网格抗扭曲能力强，计算效率和计算精度高，所以对齿轮进行网格划分时选用高质量的六面体网格，对齿轮的性能分析意义重大[16]。通过位置方程求解齿面上任一个网格节点的位矢和法矢；根据凸面和凹面对应的节点，合理地设计齿厚方向网格节点密度。

考虑到齿轮的工作寿命与最大弯曲应力值的六次方成反比，即弯曲应力略微减小，就会使得齿轮的工作寿命大幅度的提高[17]。在齿根过渡曲线处，齿轮形体发生突变，产生应力集中现象，模型沿齿根过渡曲线进行网格加密处理，划分6个节点。

弧齿锥齿轮的基本参数如表1所示，表2为大轮和小轮加工参数。

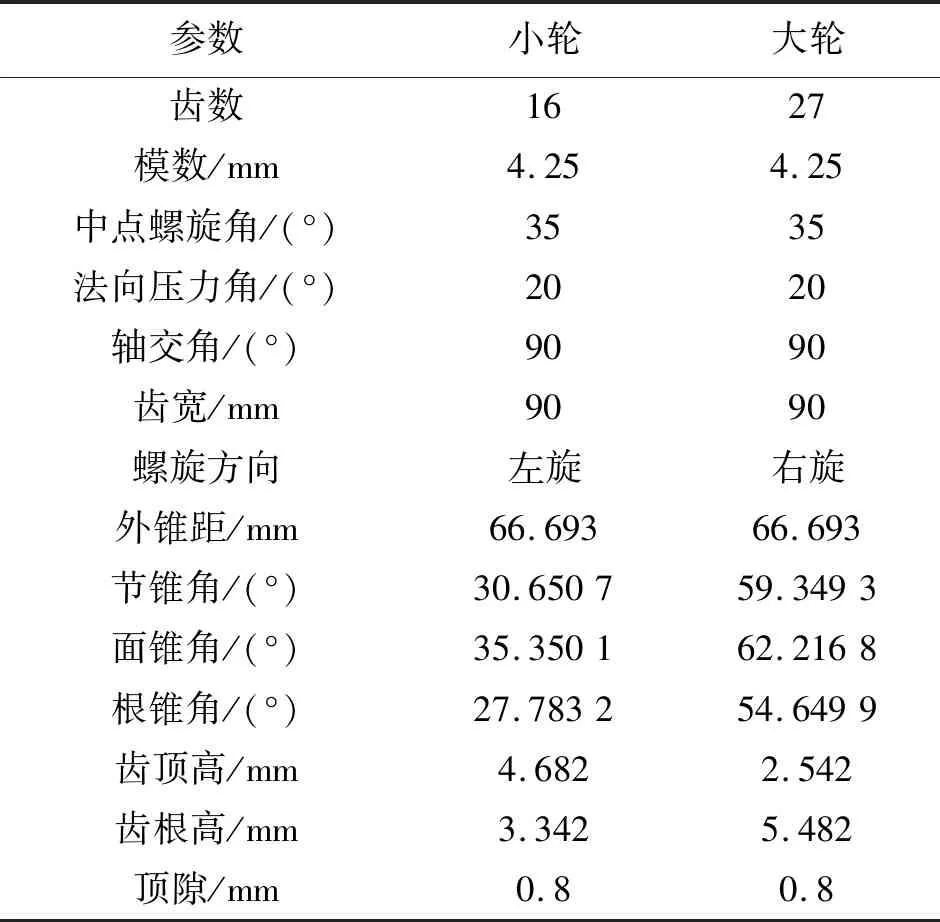
表1 弧齿锥齿轮的基本参数

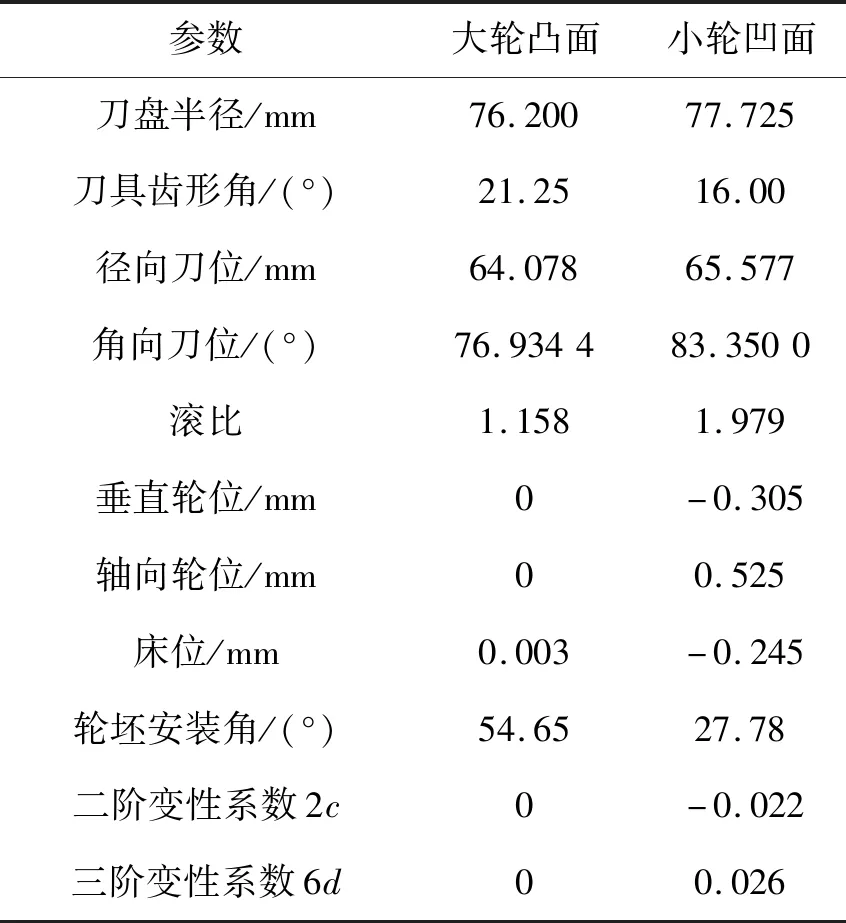
表2 大轮、小轮加工参数

图2为通过轮齿接触分析得到的齿轮副工作面齿面印痕和传动误差图。基于计算的传动误差，求得啮合路径每一瞬时接触点上的主从动齿轮啮合转角，通过坐标变换得到弧齿锥齿轮单齿有限元装配模型。

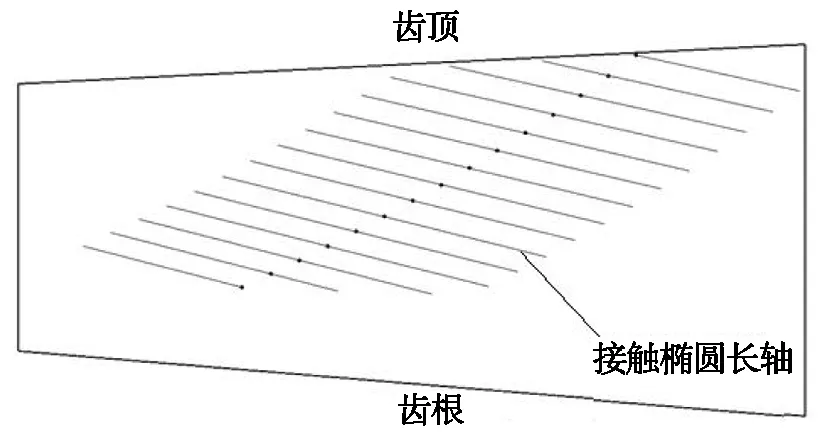
(a) 大轮齿面接触印痕

按照inp文件格式，将有限元装配模型节点及网格信息储存在inp文件中，导入有限元软件，可得到在正确装配位置下的有限元模型，五齿有限元装配模型如图3所示。

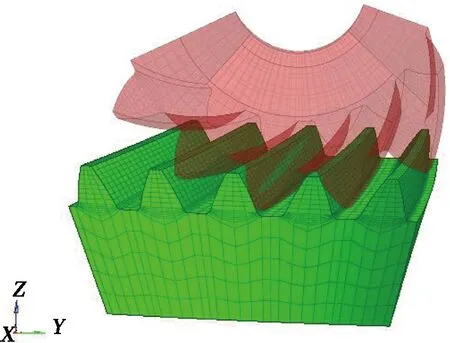
图3 弧齿锥齿轮五齿有限元装配模型

1.2 有限元模型前处理

在ABAQUS软件中进行有限元接触分析，对装配好的五齿模型设置如下：

材料属性：齿轮大小轮材料均为合金钢，杨氏模量E为2.1×105MPa、泊松比σ为0.3、密度ρ为7.9×10-9t/mm3。

接触对：定义接触面，包括轮齿凸面和凹面、相邻齿间的齿根过渡区域、齿顶过渡区域。齿轮在啮合过程中会出现相互浸透现象，这将直接影响求解器计算的进程和精度[18]。为避免浸透现象的发生，按照主面和从面的选择规则[19-20]，大轮齿面为从面，小轮齿面为主面，建立接触对。

耦合点：取大轮、小轮旋转轴线上一点为参考点，将齿轮内圈和轮毂断面耦合在参考点上，方便边界条件的施加。

分析步：采用隐式静力学分析方法，为保证有限元分析计算收敛，设置2个分析步。第1个分析步消除齿侧间隙，使两啮合齿面接触，保证初始接触迭代计算收敛，时间为1 s。第2个分析步时间设置为3 s。

边界条件和载荷：小轮全约束，大轮开放绕自身旋转自由度，并施加扭矩。

2 承载接触分析

2.1 接触应力

图4为大轮施加30 N·m时各接触位置的齿面接触应力分布云图。齿轮在正常啮合过程中，单齿啮合时接触应力值最大，双齿啮合时，两对齿都分担载荷，此时齿面的接触应力就会减小。

通过图4分析每一瞬时齿轮的啮合运动，根据应力分布云图和接触印痕，可以看出大轮接触椭圆从大端齿顶向小端齿根逐渐移动，最大主应力位于接触椭圆的中心位置。由图4a可知：接触区域位于工作面中间部位。由图4b可以看出：大轮中间齿在退出啮合时，齿面最大接触应力位于齿顶线下侧，齿轮啮合过程中并未出现边缘接触。

2.2 承载传动误差

承载传动误差是指受载状态下，当主动轮匀速回转时，从动轮实际转角与理论转角的差值，主要由于齿轮受载后弹性变形导致，包括轮齿的弯曲变形、齿面接触变形及轮体变形等[21-22]。任意小轮转角位置转角φ下，承载传动误差EL可表示为：

EL=δφ+ET，

(2)

其中：ET为齿面接触分析得到的转角φ的几何传动误差；δφ为承载变形量，可通过有限元软件提取。

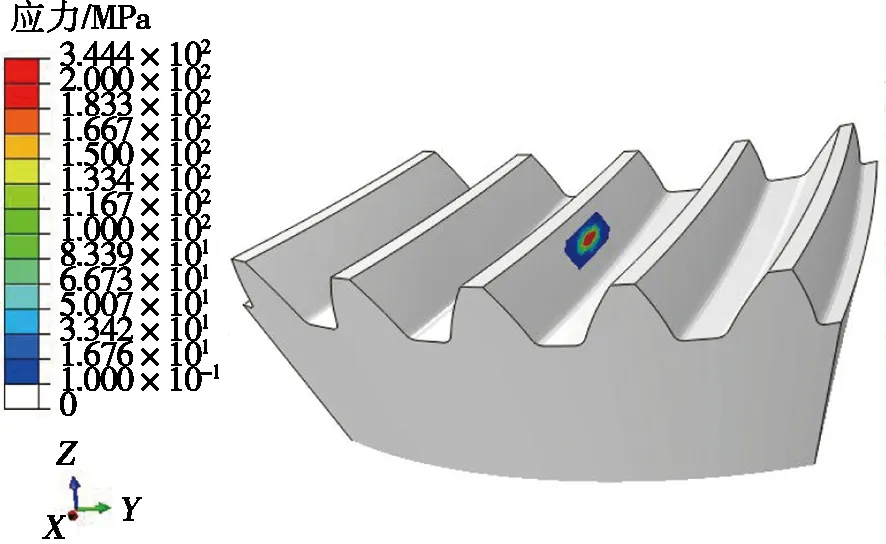
(a) 大轮中间齿单齿啮合应力分布云图

不同负载下的承载传动误差曲线如图5所示。由图5可知：负载分别为10 N·m、30 N·m和50 N·m时，承载传动误差由线波动幅值分别为18.64 μrad、11.18 μrad和31.24 μrad。承载传动误差波动先减小后增大，当负载达到50 N·m时，承载传动误差最大幅值为259.15 μrad，曲线位于几何传动误差曲线右端端点上方，处于边缘接触的临界状态。严重的边缘接触会使最大接触应力发生在齿轮齿顶或齿根处，引起轮齿强度破坏，使传动不平稳，承载传动误差曲线波动幅值较大。当负载为30 N·m时，该对齿轮副对应的承载传动误差波动最小，为11.18 μrad，传动最平稳。

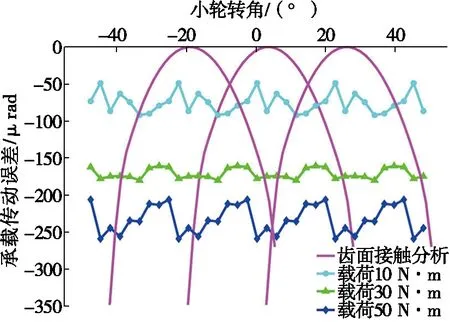
图5 不同负载下的承载传动误差曲线

3 振动分析

承载传动误差的时变性会产生动态啮合力，从而引起齿轮系统的振动噪声[23]。为了评估齿轮副的动态啮合性能，以承载传动误差为激励，利用MASTA软件进行振动分析。

图6是负载分别为10 N·m、30 N·m和50 N·m下，齿轮副前3阶啮合频率振动加速度瀑布图，第1阶啮合频率的振动加速度最大，对齿轮副整体振动的贡献度最大。

负载30 N·m的第1阶啮合频率振动加速度最大值明显最小，如图6b所示。10 N·m、50 N·m的振动加速度最大值依次增大，如图6a和图6c所示。以负载30 N·m为例，在第1阶啮合频率下，第1阶和第3阶固有频率1.66 kHz和2.19 kHz处出现较为明显的峰值，振动加速度分别为131.91 m/s2和128.93 m/s2，说明齿轮啮合频率与固有频率相同，产生共振；在第2阶固有频率2.10 kHz处，未引起齿轮副剧烈振动。

图7a为负载30 N·m工况下，动态啮合力随频率变化的曲线图；图7b为负载30 N·m工况下，相位随频率变化的曲线图；图7c为负载30 N·m工况下，柔度随频率变化的曲线图。从图7a中可以看出：动态啮合力出现两次峰值，分别位于1.66 kHz和2.19 kHz处。相位波动为0°～180°，如图7b所示。在图7c中，两条柔度曲线有3个交点，分别位于频率1.66 kHz、2.10 kHz和2.19 kHz处。

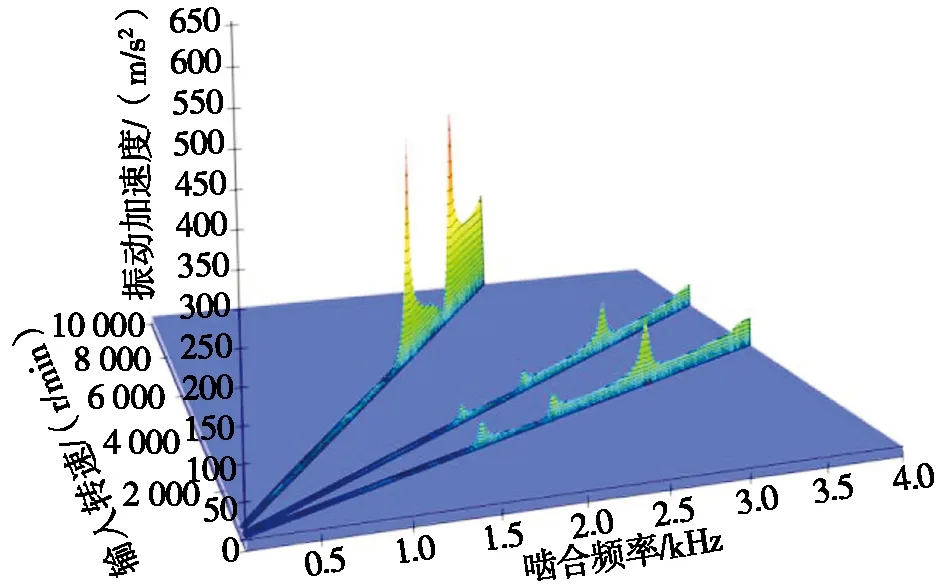
(a) 10 N·m负载下振动加速度瀑布图

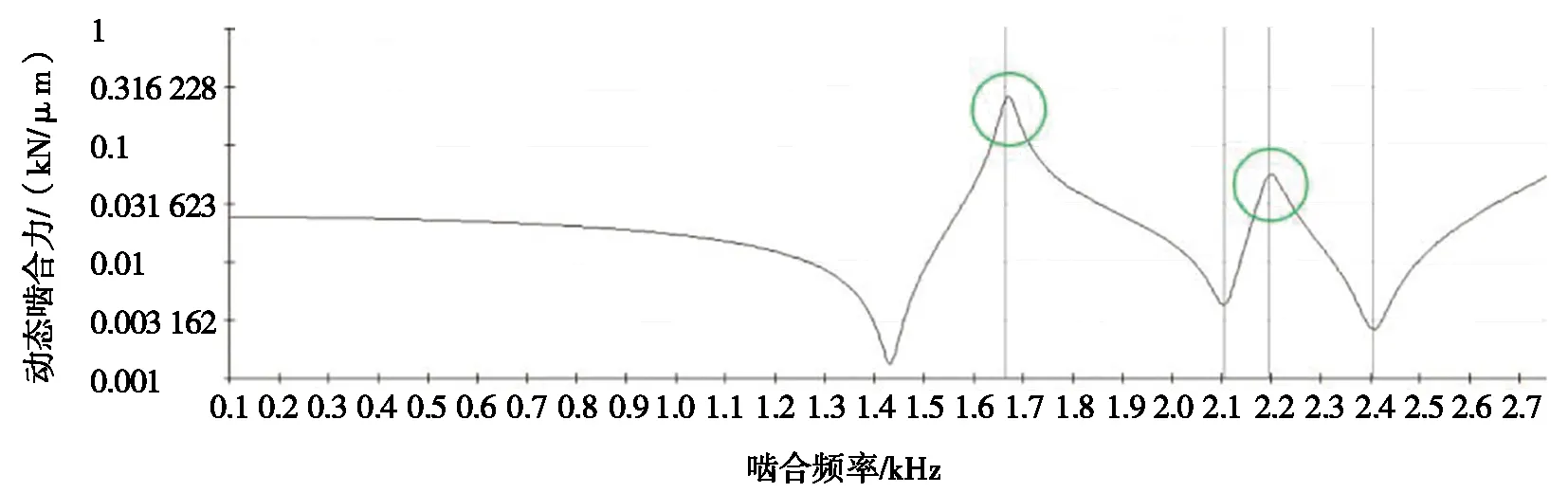
(a) 负载30 N·m工况下动态啮合力随频率变化曲线图

从图7中可以看出：当啮合频率为1.66 kHz和2.19 kHz时，齿轮副柔度绝对值相等，相位相反，动态啮合力出现峰值；啮合频率为2.10 kHz时，齿轮副柔度绝对值不相等，且相位相差不为180°，虽然啮合频率等于固有频率，但未引起齿轮副剧烈振动。结合图6和图7，通过啮合频率和固有频率相等可以找出潜在共振发生的区域，只有当齿轮副柔度绝对值相等、相位相反时，齿轮动态啮合力出现峰值，才引起齿轮副的剧烈振动。结合图5中齿轮在不同负载下的承载传动误差波动曲线，齿轮发生共振时，降低承载传动误差波动，可以有效地降低齿轮振动加速度幅值。

4 试验验证

基于锥齿轮闭功率流疲劳寿命试验台，使用M+P动态信号分析仪，对弧齿锥齿轮传动系统进行振动试验。M+P动态信号分析仪适用于所有振动噪声、声学和一般动态信号测量，可提供试验测试方案。图8为锥齿轮闭功率流试验台，将传感器固定在距离啮合位置较近的主动轮轴上方，图9为传感器放置位置。

图8 锥齿轮闭功率流试验台

图9 传感器放置位置

设置输入轴转速为540 r/min，从动轮负载分别为10 N·m、30 N·m和50 N·m，测得的轴向振动信号如图10所示。

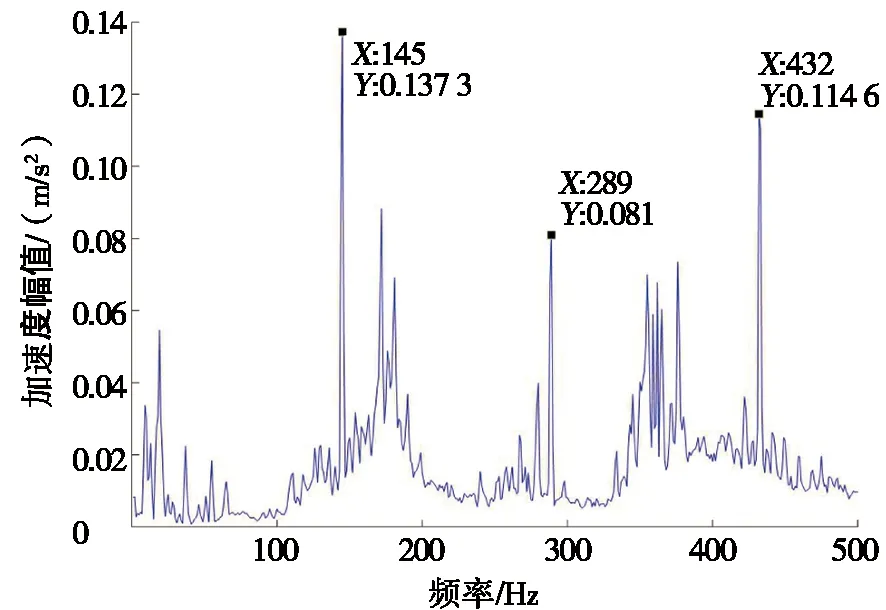
(a) 转速540 r/min、负载10 N·m

由图10可以看出：不同工况的频谱图中都包括弧齿锥齿轮的啮合频率和谐波分量，并且第1阶啮合频率处的振动加速度值最大，与图6的振动加速度瀑布图分析结论一致。在转速相同的条件下，分析第1阶啮合频率处的振动加速度，可以看出：30 N·m负载下的振动加速度幅值最小，为0.109 7 m/s2，而50 N·m负载下的振动加速度幅值最大，为0.180 2 m/s2，随着负载从10 N·m增加到30 N·m和50 N·m，振动加速度先减小后增大，与图5的承载传动误差分析规律一致。为保证弧齿锥齿轮副具有较好的动态啮合性能，应使负载工况下的承载传动误差幅值波动最小。