基于有限元与神经网络的含裂纹缺陷管道安全性分析
2021-07-22刘昌华殷海龙白瑞峰裴梦琛
刘昌华,殷海龙,白瑞峰,裴梦琛,武 玮
(1.西北大学 化工学院, 陕西 西安 710069;2.西安交通大学 化学工程与技术学院, 陕西 西安 710049)
随着远距离输送油气的要求,油气管道逐渐成为油气输送的主要形式。与水、陆等运输方式相比,管道运输具有运输量大、便于管理、安全可靠、迅速快捷等优势。目前绝大多数管道都敷设在地下,面临着土壤腐蚀的风险[1-5]。当管道因腐蚀产生表面缺陷时,管道表面的几何连续性遭到破坏,在管道外载荷作用下,缺陷部位会产生应力集中,管道承压能力将被严重削弱,严重的将导致管体穿孔或破裂,引起安全事故[6-10]。在诸多的腐蚀缺陷中,裂纹缺陷因其随机性、突发性和难检测性对管道安全服役的影响最大。因此对含裂纹型缺陷的管道开展缺陷评估,掌握其安全状态,为后续制定实施合理的防护措施至关重要。目前对含缺陷管道进行评定的主要标准规范有ASME B31G、DNV RP-F101、GB/T19624等[11-12],但这些规范评定的结果通常偏于保守。另外的方法是采用有限元分析技术对含缺陷管道进行分析[13-14],尽管这种方法的评定结果准确性高,但需要根据不同的情况构建不同的有限元模型,实施难度大,效率低。而机器学习技术,特别是人工神经网络,能够从大量数据中学习数据之间内在关联关系,构建合理预测模型。基于此,本文通过有限元方法和前馈神经网络,分析裂纹处最大应力和KI的变化规律,构建能够准确预测含裂纹型缺陷管道的最大应力和应力强度因子的预测模型,为准确便捷实施管道安全分析提供技术支持。
1 管道有限元模型构建
本文的研究对象为X80钢制管道,管道外直径为914 mm,壁厚为16.9 mm。材料参数:弹性模量190 GPa,泊松比0.3,屈服强度550 MPa。采用非线性有限元建模,材料使用双线性各向同性应力应变关系模型。管道几何模型长度设定为2 000 mm, 以消除管道边界载荷对管道裂纹处应力状态的影响(见图1)。裂纹采用半椭圆二维裂纹形式,位于管道外壁面正中间。管道两端采用固支边界条件,内部施加均布应力。网格选定为四面体网格,为了准确捕捉裂纹处的应力状态,在进行网格划分时对裂纹部位加密处理,并进行了网格无关性检验,图2为模型网格和裂纹处网格局部细化图。
采用上述模型模拟管道在承受3.0 MPa、5.0 MPa、 7.0 MPa内压条件下,裂纹长度为壁厚的10%~100%,裂纹深度为壁厚的10%~90%时,裂纹处的最大von Misses等效应力和应力强度因子KI,共计270组数据。
图1 埋地管道几何模型Fig.1 Geometric model of buried pipeline
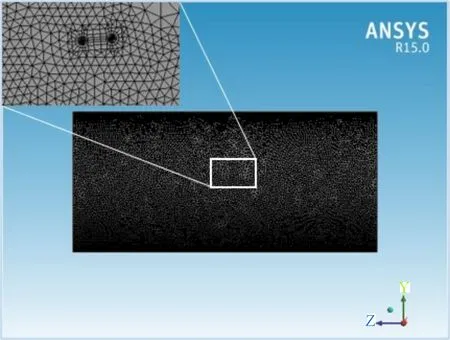
图2 网格划分及裂纹局部网格细化图Fig.2 Mesh generation and local mesh refinement of cracks
2 神经网络预测模型构建
采用前馈神经网络模型,利用有限元模拟获得的数据进行训练,构建能够准确预测含轴向外表面裂纹管道的最大应力和应力强度因子KI的预测模型。本文采用Levenberg-Marquardt(LM)算法优化网络参数,LM算法是一种先进的非线性优化算法,与最常用的反向传播算法相比,它的收敛速度更快、稳定性更好[15]。图3为前馈神经网络结构图。根据多次试验,确定网络结构为1个输入层(3个节点),1个隐藏层(12个节点)和1个输出层(1个节点),随机将270组数据中的70%作为训练集,15%作为验证集,15%作为测试集。
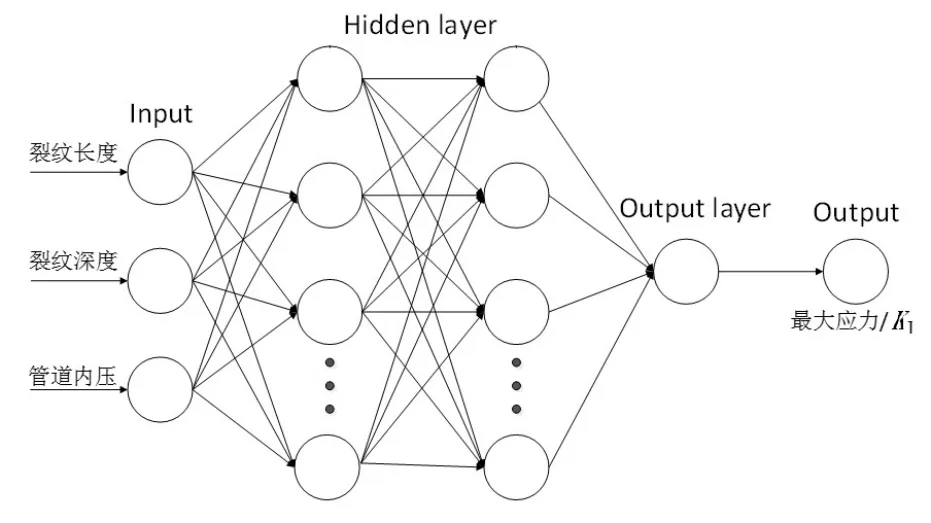
图3 前馈神经网络结构Fig.3 Feedforward neural network
3 结果与讨论
3.1 影响因素相关性分析
为了明确管道应力状态与裂纹特征参数(深度和长度)及管道内压之间关联关系强弱,需要对其各参数之间的相关性进行分析。本文根据有限元模拟数据,采用Peason相关分析方法计算各影响因素之间的相关系数,结果如图4所示。从图中可以看出,裂纹深度a、长度c和管道内压P与最大应力和KI呈正相关。与裂纹长度相比,裂纹深度与最大应力和KI相关性稍大。与裂纹尺寸相比, 管道内压与最大应力和KI的相关性更大。尤其是与KI的相关性,管道内压(0.70)明显高于裂纹深度(0.47)和裂纹长度(0.44)。
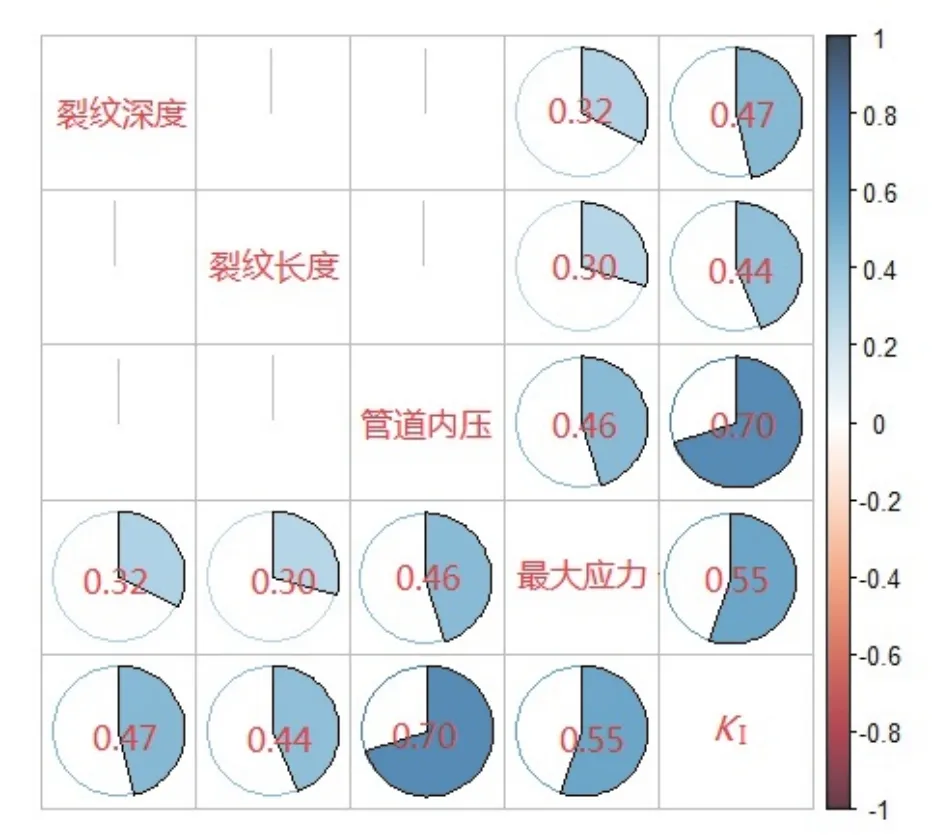
图4 各变量之间的相关性分析Fig.4 Correlation analysis among variables
3.2 管道内压对管道力学状态的影响
图5为管道内压对管道裂纹处最大应力和KI的影响(以深度为30%壁厚的裂纹为例)。如图所示,随着管道内压增大,裂纹处最大应力呈现增大趋势,但当最大应力超过材料屈服强度550 MPa后,受裂纹尖端应力松弛影响,管道内压对裂纹最大应力的影响变得很小。对于KI而言,随着管道内压增大,KI越大。且对于同样深度的裂纹,长度越大,KI随内压的增大幅度也越大。
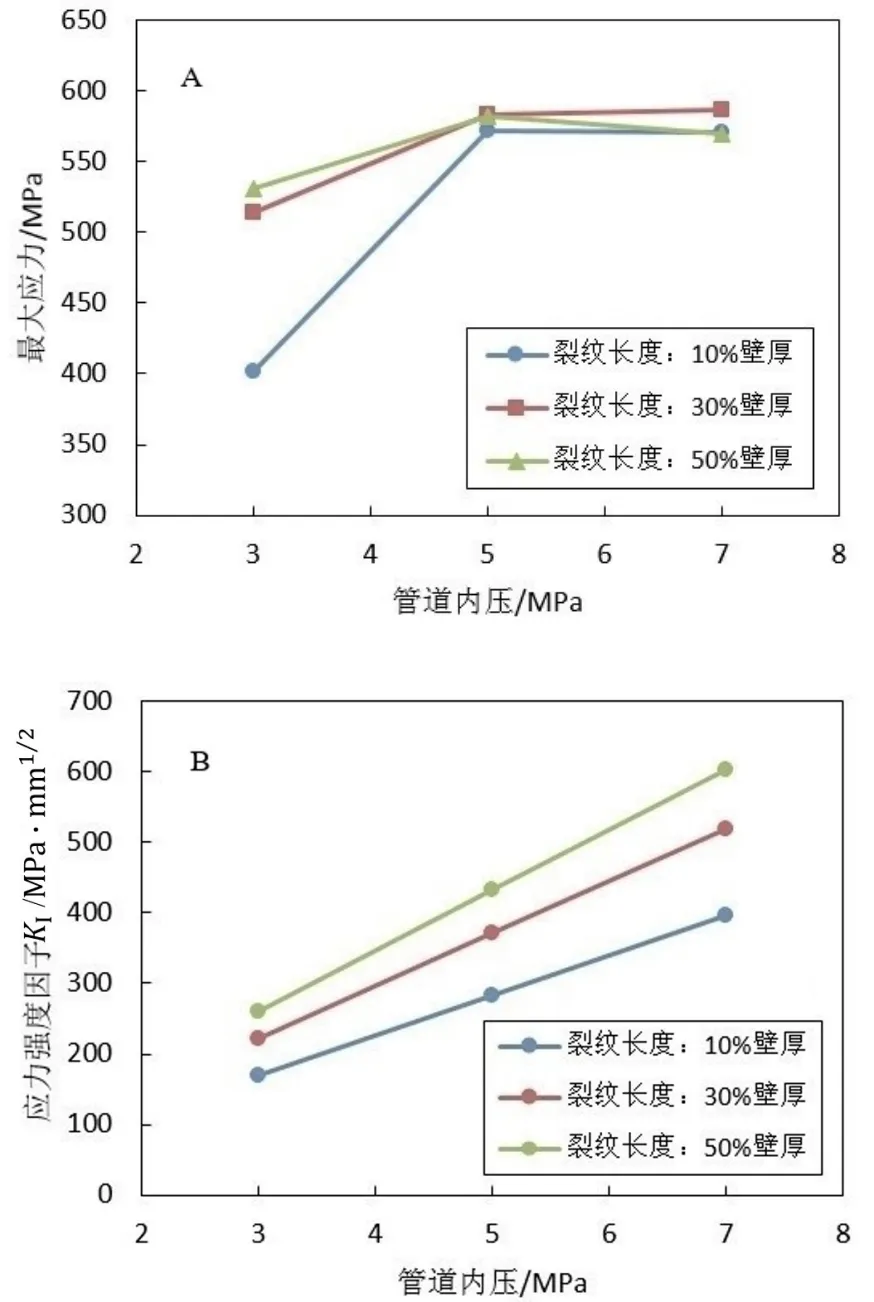
图5 管道内压对管道最大应力(A)和KI(B)的影响Fig.5 Influence of internal pressure on maximum stress and KI of pipeline
3.3 裂纹深度对管道力学状态的影响
在不同的管道内压条件下,裂纹特征参数对管道力学状态的影响规律相似。下面以管道内压3 MPa为例分析裂纹深度对管道最大应力和KI的影响,结果如图6所示。由图可知,管道的最大应力随裂纹深度的增加而增大,裂纹长度越小,最大应力随裂纹深度的增长速度越慢,当管道的最大应力超过材料屈服强度550 MPa之后,最大应力开始缓慢上升,受应力松弛的影响会有略微的降低,最终稳定在580 MPa左右。KI随着裂纹深度的增加而增大;裂纹长度越大,KI的增大幅度越大;同一深度裂纹下,裂纹长度越大,KI越大。
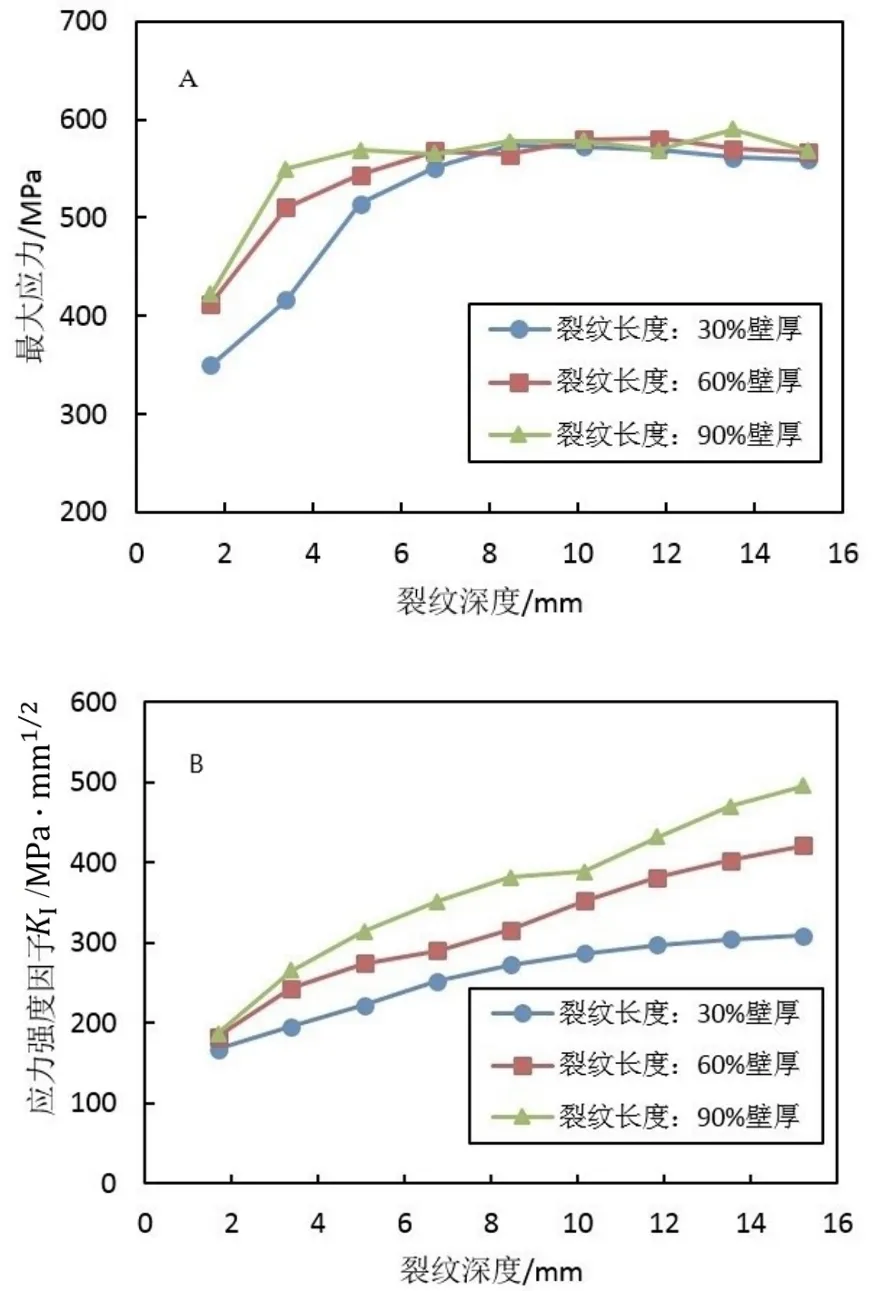
图6 裂纹深度对管道最大应力(A)和KI(B)的影响Fig.6 Influence of crack depth on maximum stress and KIof pipeline
3.4 裂纹长度对管道力学状态的影响
图7是管道内压为3 MPa时,裂纹长度对管道最大应力和KI的影响。管道的最大应力随着裂纹长度的增加而增大,裂纹深度越小,最大应力随裂纹长度的增长速度越慢,同样地,当管道的最大应力超过材料屈服强度550 MPa之后,最大应力开始缓慢上升,受应力松弛的影响会有略微的降低,最终最大应力稳定在580 MPa左右。KI随着裂纹长度的增大而增大,裂纹深度越大,KI的增大幅度越大。同一深度裂纹下,裂纹长度越大,KI越大。
3.5 神经网络模型预测性能分析
为了验证本文所建前馈神经网络的预测性能,运用预测模型对测试集数据进行预测,并与实际值进行比较,结果如图8所示。由图8可知,最大应力预测模型R=0.981 2,当裂纹深度为3.38 mm,长度为16.9 mm,管道内压为3 MPa时,预测误差最大,此时预测值为530.33 MPa,实际值为551.92 MPa,相对误差为3.91%。最大KI预测模型R=0.998 0,当裂纹深度为1.69 mm,长度为5.07 mm,管道内压3 MPa为时,预测误差最大,此时预测值为148.15 MPa·mm0.5,实际值为167.50 MPa·mm0.5,相对误差为11.55%。由此可以看出,文中所建预测模型的预测误差较小,结果较为准确,能够为实际缺陷安全评定提供可靠的预测数据。
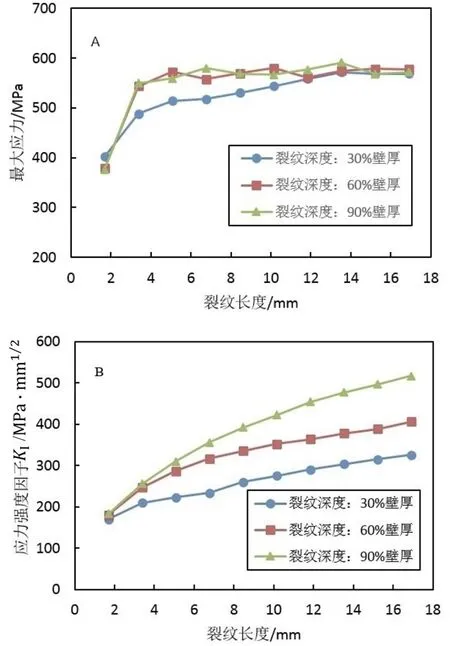
图7 裂纹长度对管道最大应力(A)和KI(B)的影响Fig.7 Influence of crack length on maximum stress and KI of pipeline
4 结语
本文利用有限元方法和前馈神经网络研究了含轴向外表面裂纹管道的最大应力和KI的变化规律,构建了相应的预测模型。结果表明,最大应力随着管道内压、裂纹深度以及裂纹长度增加而增大,当最大应力超过材料屈服强度(550 MPa)后,受裂纹处应力松弛的影响,增大趋势放缓,最终稳定在580 MPa左右。而应力强度因子KI则随着管道内压、裂纹深度以及裂纹长度增加而增大。本文所构建的最大应力和KI预测模型的预测结果准确,最大误差小于12%,研究结果可为含裂纹缺陷油气管道的安全评定提供技术支持。
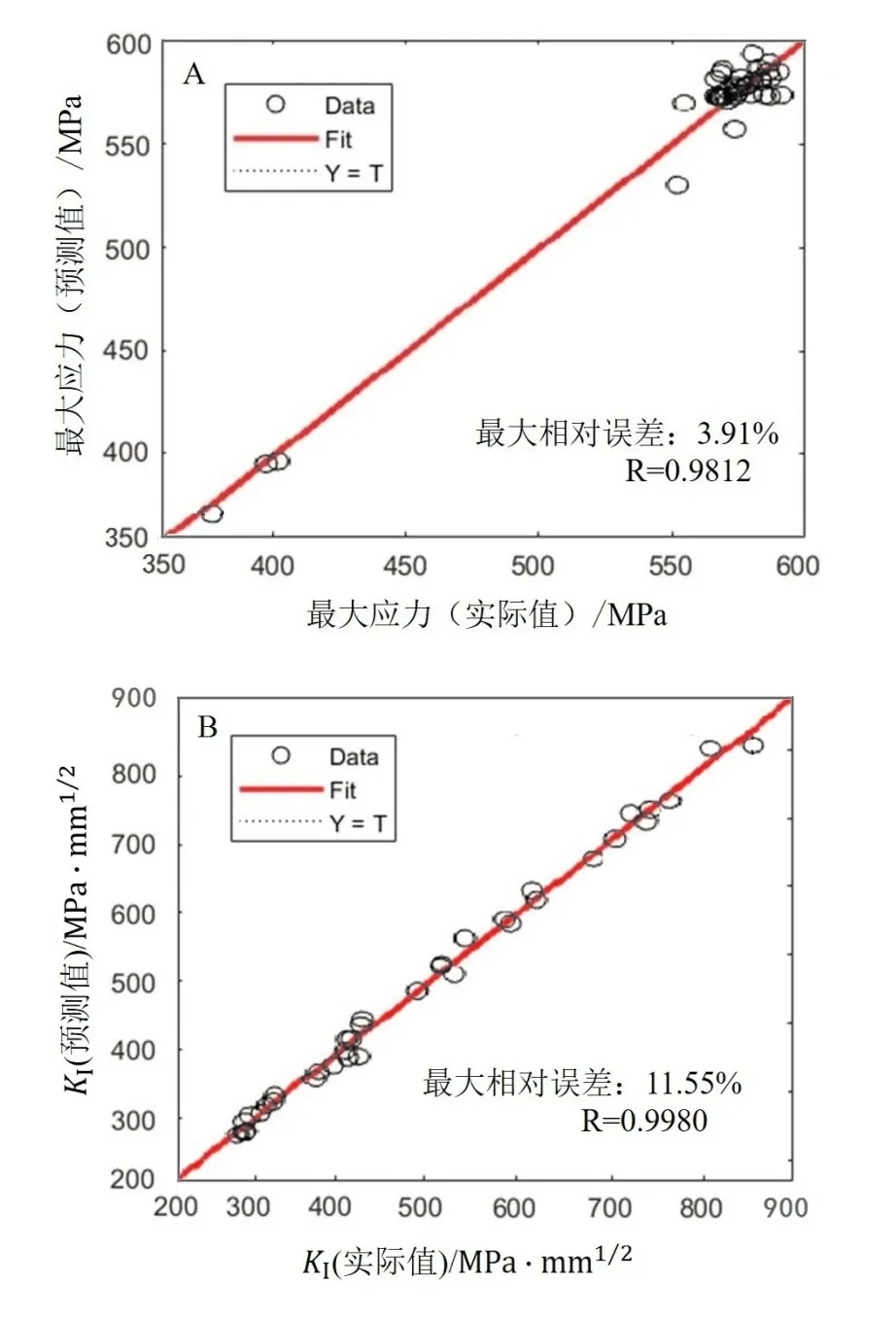
图8 神经网络模型测试集实际结果(A)与预测结果(B)比较Fig.8 Comparison of actual and predicted results of neural network model test set
