三支决策
——基于管理研究视角
2021-07-22刘盾
刘 盾
(1.西南交通大学 经济管理学院,四川 成都 610031;2.重庆邮电大学 计算智能重庆市重点实验室, 重庆 400065)
三支决策(three-way decision, 简称3WD)是由加拿大学者姚一豫提出的一种基于认知科学的朴素哲学思想和不确定决策理论[1],它与粗糙集、模糊集、云计算、形式概念分析等一起成为粒计算与知识发现领域的代表性研究理论和方法。三支决策的核心思想是借鉴人类的思维方式和行为模式,通过分治模型和序贯策略,采取三分而治和化繁为简来分析和解决复杂决策问题。由于其在决策过程中符合人类认知特点,且在处理不确定性问题时具有很好的可解释性、价值性和可行性,在经历40余年的发展后,已逐渐成为一种处理不确定问题的重要理论和方法,受到国内外学者的广泛关注。
三支决策最早思想是来源于波兰数学家Pawlak提出的粗糙集理论(rough sets theory),粗糙集理论通过上下近似集对论域进行划分,所得到的正域、边界域和负域自然形成了3个互补相交的部分。然而,粗糙集的三分策略只给出了划分的语法解释,而没有提供相应的语义解释。为了解决上述缺陷,姚一豫提出了决策粗糙集模型[2],通过引入贝叶斯风险最小准则来获取相应划分阈值,这为三支决策语义研究提供了一种新的途径。随着粒计算理论的发展,粒计算的三元论也随之被提出[3]。在粒计算三元论中,哲学思想、研究方法和计算范式构成了三元论等边三角形的3个顶点。进一步地,基于“一分为三”的哲学论、“三分而治”的方法论和“三项式、三点式、三足式”的计算论也成为三支决策研究的基本出发点。值得一提的是,三支决策研究核心理论的正式确立是姚一豫提出的TAO模型(Trisecting-Acting-Outcome模型,也称“分-治-效”模型)[4]。“分”包含“分、合、序”3个要素,对应了“一分为三”“三合为一”“序贯分析”3种方法;“治”包含“点、线、面”3种策略,反映了“一维”“二维”和“三维”3个维度;“效”包含“简、优、快” 3个方面,体现了“简单易懂”“优异完善”和“快速高效”3类要求。其中,“分”是“治”的前提,“治”是“分”的目的,而“效”是“分”和“治”的监督保障。可以看到,TAO模型给出了一个三支决策一般性理论研究框架,并对三支决策内涵和外延作了诠释和扩展,三支决策相关研究也从基于粗糙集的狭义视角拓展为三要素、三部分、三分量、三层次、三阶段、三步骤、三分类等广义认知。
一般而言,三支决策的发展可分为孵化期(1980—2006)、羽化期(2007—2016)和成长期(2017至今)3个时期。经过40余年的发展,三支决策不仅在理论和方法上取得了巨大进展,也在信息、工程、医疗、管理等领域得到了成功应用。从学科视角来看,三支决策研究主要集中于数学、信息和管理三大领域[5]。其中,数学领域关注三支决策的粒度描述和粒度表示;信息领域聚集于三支决策的粒度选择、粒度计算和粒度优化;管理领域集中于三支决策的粒度解释和粒度应用。就三支决策管理相关研究而言,主要也可从理论模型和方法应用两个方面去回顾。对于前者,刘盾和梁德翠等研究了随机、区间、模糊等不确定性决策环境下,当损失函数为不同不确定性数学测度时,相应三支决策阈值的求解方法[6-10];张楠等将效用函数替换损失函数,提出一种效用三支决策模型[11];Liu等将前景理论引入到三支决策中,提出一种前景三支群决策方法[12]。Liang等探讨了基于后悔理论的风险区间值三支决策模型,并进一步考虑了区间二型模糊环境下的行为三支决策模型[13-14]。Wang等给出了一系列基于前景理论、累积前景理论和后悔理论的三支决策扩展模型[15-17]。Lang等考虑了三支决策冲突问题,并建立了相应的数学模型[18]。Sun等探讨了双论域下的多属性三支决策冲突问题[19]。对于后者,Zhou和Liu分别讨论了基于贝叶斯理论和Logistic回归的多分类三支决策方法[20-21]。Zhan等提出了基于排序信息下的多属性三支决策方法[22]。Zhang和Wang分别探讨了基于随机森林、回归分析和主动学习的三支推荐系统及其应用[23-24]。Li等将序贯三支决策思想引入到人脸识别和图像处理中,取得了良好的应用效果[25]。Liu等将三支决策方法引入到政策制定和石油开采问题中,提出以利润最大化为目标的三支决策方法[26]。Zhou等将三支决策思想应用到垃圾邮件过滤上,并从管理视角分析了延迟决策策略对邮件分类的影响[27]。Liang等将三支决策和群决策理论相融合,研究了三支群决策在社交网络、文本挖掘中的应用[28-29]。李波和高晓光系统地探讨了基于三支决策的空战应用问题[30]。此外,国际重要学术期刊InformationSciences,InternationalJournalofApproximateReasoning,Knowledge-basedSystems,InternationalJournalofMachineLearningandCybernetics,CognitiveComputation等也分别出版多期专辑、专刊介绍三支决策的最新研究成果;国际粗糙集学会(IRSS)和中国CAAI粒计算与知识发现专委会(CGCKD)也组织了多次三支决策分论坛;国内外学者从2010年起,也相继出版了《三支决策理论与应用》[31]《三支决策与粒计算》[32]《三支决策: 复杂问题求解方法与实践》[33]《粒计算、商空间及三支决策的回顾与发展》[34]《多粒度与三支决策》[35]《三支决策理论与方法》[36]《三支概念分析与决策》[37]《三支决策与大数据分析》[38]等多部专著;三支决策学习网站(http:∥www2.cs.uregina.ca/~twd/)和“三支决策与三支计算”微信公众号也先后建成,来介绍和发布相关三支决策最新研究进展。
本文在充分调研、整理和分析已有研究文献的基础上,从管理视角出发,首先,剖析了三支决策的哲学与管理思想;其次,结合三支决策TAO模型,提出了三支决策需要解决的3个问题;然后,分析了效用三支决策与行为三支决策相关模型和方法;再者,给出了动态三支决策的研究框架;最后,对三支决策在管理领域的未来研究方向作出展望。
1 三支决策的哲学与管理思想
三支决策是一种朴素的不确定性理论和方法,它与中国传统文化中儒家的“中庸之道”和道家的“道法自然”思想有着异曲同工之妙。中庸之道思想最早源自孔子的《论语庸也》:“中庸之为德也,其至矣乎。”它诠释了一种不偏不倚,折中调和的基本处世原则。老子的《道德经》也讲到:“道生一,一生二,二生三,三生万物。”这里,“一、二、三”分别指的是“天、地、人”,而“道生万物”揭示了从少到多,从简单到复杂的过程,也诠释了道家“天人合一”的哲学思想。孟子在《孟子·公孙丑下》谈到:“天时不如地利,地利不如人和”。 孟子认为,天时、地利、人和都是影响战争胜败的重要因素,在这三者之中,人和是最重要的。再者,《论语先进》中的“过犹不及”和《孟子尽心章句下》中的“尽信书,则不如无书”都提及“一分为三”的思想,把做事和读书分为“过、及、不及”和“尽信、信、不信”3种境界,强调“三”的辩证哲学思想。类似地,中国传统的管理思想讲顺道、重人、人和、守信、利器、求实、对策、节俭、法治,这里面也有很多论点与三支决策思想一脉相承。我国春秋时期著名的军事家孙子在《孙子·谋攻篇》写道:“知彼知己,百战不殆;不知彼而知己,一胜一负;不知彼,不知己,每战必殆”,这充分说明了知己知彼百战百胜的道理。孙子在《孙子兵法·谋攻篇》又写道:“上兵伐谋,其次伐交,其次伐兵,其下攻城”,讲述了上兵伐心,中兵伐谋,下兵伐力的道理。左丘明在《左传·庄公十年》的《曹刿论战》提出军事指挥策略:“一鼓作气,再而衰,三而竭”,阐述士气对战争胜负的影响。苟子在《苟子王霸篇》说道:“农夫朴力而寡能,则上不失天时,下不失地利,中得人和而百事不废”,这说明农时、土壤肥沃和分工3个要素对耕作的重要性。现代著名作家秦牧在其随笔集《艺海拾贝酷肖》中收录了近代书画大师齐白石说过的一段话:“作画妙在似与不似之间,太似为媚俗,不似为欺世”,其中,“似与不似”体现了艺术鉴赏的一条美学原则。此外,还有很多典故体现“三”的哲学和管理思想。《论语·述而》讲“三人行,必有我师焉”;《论语·学而》讲 “吾日三省吾身”;《三国演义》讲“三个臭皮匠,顶个诸葛亮”。在中国成语中也有三顾茅庐、三人成虎、孟母三迁、连中三元等耳熟能详的故事。总而言之,三支决策思想反映了古代先贤智慧,与中国传统的哲学和管理思想高度契合,这对于复杂决策环境和大数据管理问题具有重要的理论指导和方法借鉴意义。
2 三支决策与TAO模型
假设S=(U,R)为一信息系统,其中:U={x1,x2,…,xn}表示论域,它是对象的非空有限集合;R是定义在论域U上的一种二元关系。三支决策通过函数f将论域U划分为3个两两互不相交的区域:U1-域、U2-域和U3-域,即
f:U→{U1,U2,U3}
(1)
其中,U1,U2,U3⊆U,U=U1∪U2∪U3;U1∩U2=∅,U2∩U3=∅,U1∩U3=∅。其补集的构造如下:
(2)
对于被划分的3个区域U1、U2和U3,分别利用3种不同的策略S1、S2和S3,采取3种不同的行动a1、a2和a3,得到3种不同的评价结果O1、O2和O3,这自然形成了TAO模型的核心思想。图1展示了TAO模型的基本理论框架。
在图1中,三支决策需要解决3个问题:①如何对论域进行三分?②如何制定策略和采取相应行动?③如何评价决策效果?
问题1关键步骤是如何选取合适的阈值α和β,将论域分为3个互不相交的子论域。下面,以概率粗糙集和决策粗糙集为例来阐明上述思想。
定义1假设论域U是一个有限非空子集,R是定义在U上的一种等价关系。记
apr(α,β)=(U,R)
为概率粗糙近似空间, 对于X⊆U, 令0≤β<α≤1,则对论域的三划分POS(α,β)(X),BND(α,β)(X)和NEG(α,β)(X)可分别定义为:
(3)
其中,Pr(X|[x])=|[x]∩X|/|[x]|表示条件概率;[x]表示x在等价关系R下所形成的等价类;|·|表示集合中元素的基数。概率粗糙集模型假定划分阈值α和β是事先给定的,而决策粗糙集是从贝叶斯风险决策视角出发,利用损失函数来求取决策总体风险最小时的三支决策划分策略,给出一种阈值自动获取的决策方法[39]。
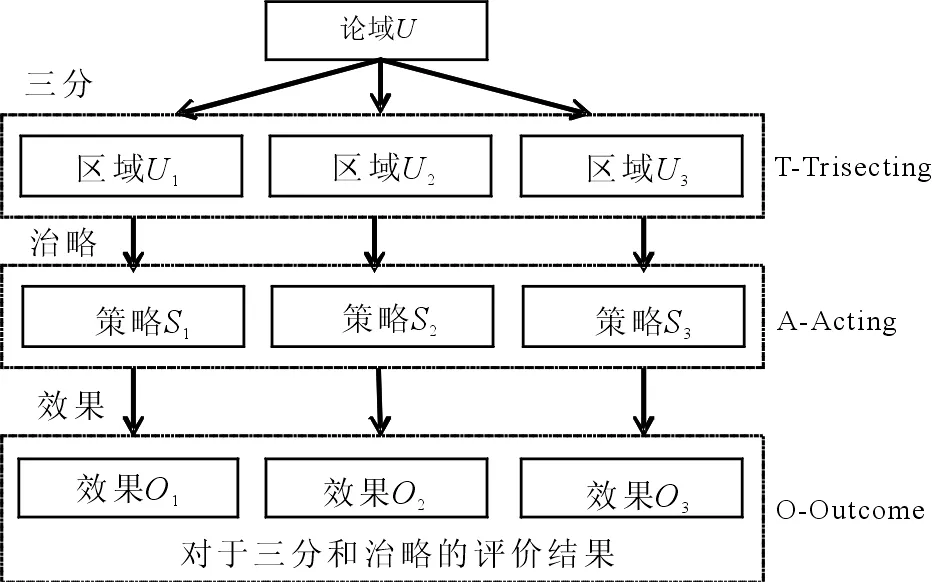
图1 TAO模型的基本理论框架图Fig.1 The basic theorem framework of TAO model
决策粗糙集模型考虑了事件的两种不同决策状态形成的集合Ω={X,X},以及表示接受、延迟和拒绝3种行动方案的集合A={aP,aB,aN}。考虑到采取不同行动会产生不同的损失,记λPP,λBP,λNP和λPN,λBN,λNN分别表示当x∈X和x∉X时,采取3种不同行动的损失函数。则采取aP,aB和aN3种行动下的总期望损失可分别表示为:
(4)
根据贝叶斯决策准则,可以选择总期望损失最小的行动集作为最佳行动方案,从而得到下面3条决策规则:
(P): R(aP|[x])≤R(aB|[x])且R(aP|[x])≤R(aN|[x])同时成立,则x∈POS(X);
(B): R(aB|[x])≤R(aP|[x])且R(aB|[x])≤R(aN|[x])同时成立,则x∈BND(X);
(N): R(aN|[x])≤R(aP|[x])且R(aN|[x])≤R(aB|[x])同时成立,则x∈NEG(X)。
由于Pr(X|[x])+Pr(X|[x])=1,规则(P)~(N)只与条件概率Pr(X|[x])和损失函数λ··(·=P,B,N)有关。此外,假设损失函数间的大小关系满足:λPP≤λBP<λNP和λNN≤λBN<λPN。将条件概率关系和损失函数关系代入到式(4)中,则决策规则(P)~(N)可改写为:
(P1): 如果Pr(X|[x])≥α,则x∈POS(X);
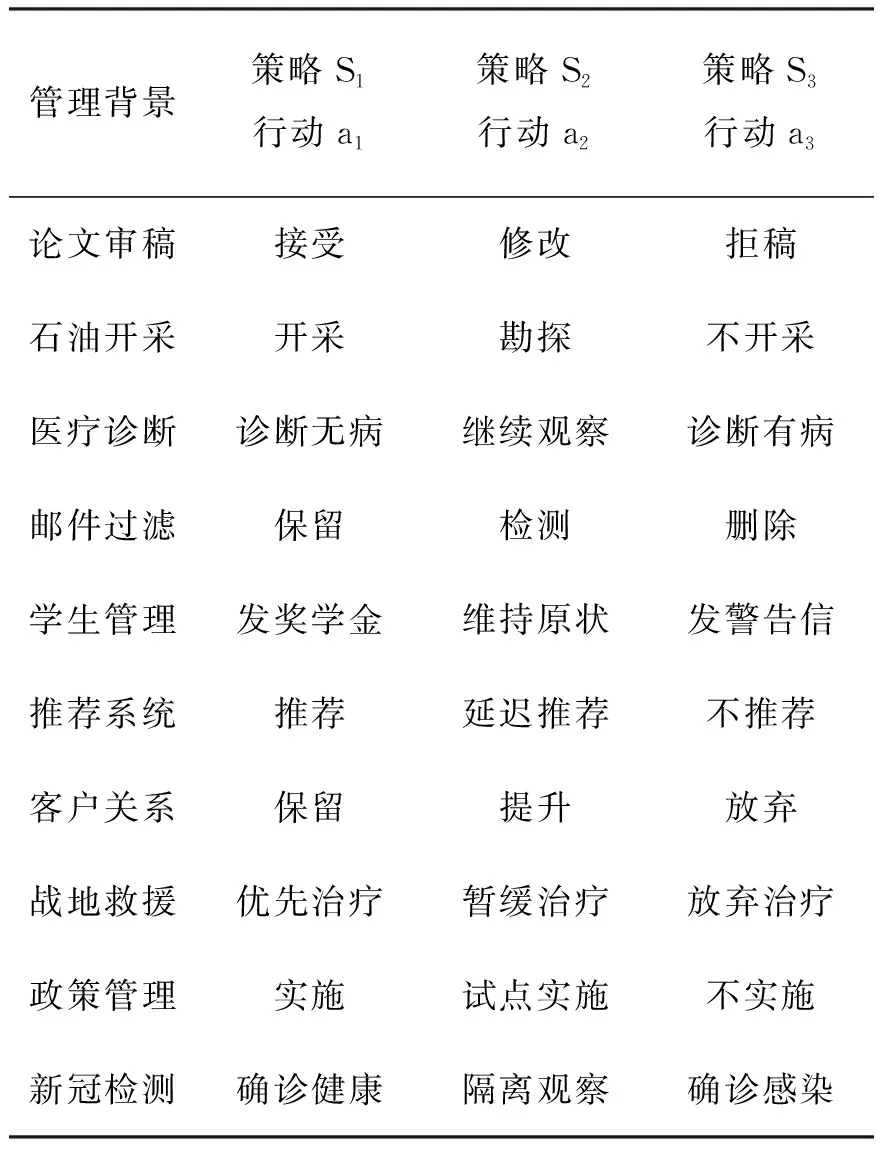
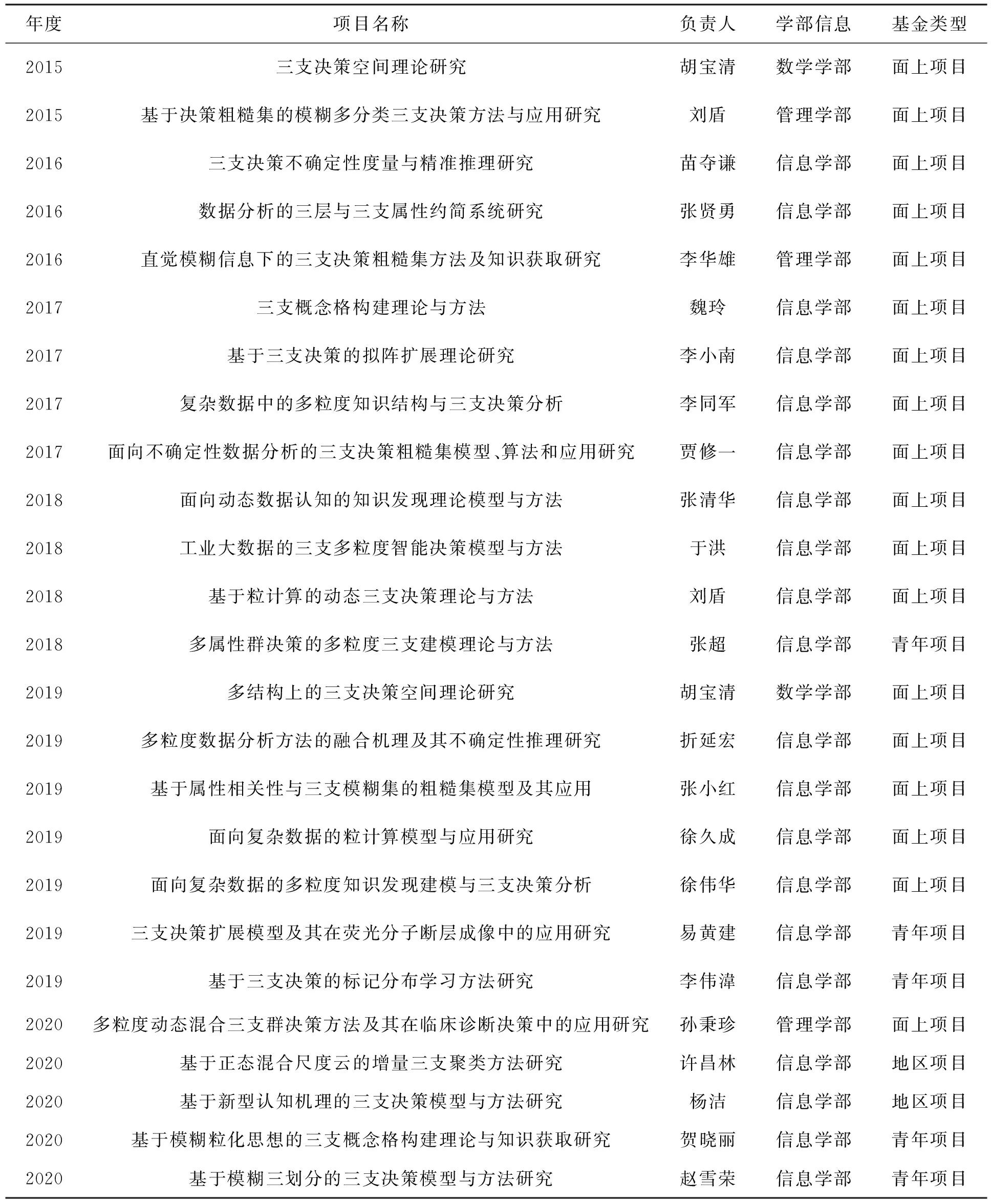
(B1): 如果β (N1): 如果Pr(X|[x])≤β,则x∈NEG(X)。 可以看到,相较于概率粗糙集模型,决策粗糙集进一步考虑了论域三划分过程中的语义问题。特别地,当U1=POS(α,β)(X),U2=BND(α,β)(X),U3=NEG(α,β)(X);a1=aP,a2=aB,a3=aN时,决策粗糙集可视为图1中TAO模型的一个特例。 问题2其核心要素是考虑问题实际应用背景和管理现实意义。 事实上,在粗糙集理论中,上下近似集将论域划分为正域、边界域和负域,3个区域自然形成3种策略,即:从正域里获取的正规则用以表示接受某事物;从负域里获取的负规则用以表示拒绝某事物;而落在边界域上的第三种规则用于表示延迟决策某事物。上述决策过程与人们认知行为是一致的。具体而言,在实际决策过程中,人们对于具有充分把握接受或拒绝的事物能够立即作出接受或拒绝判断;而对于那些不能够立即作出决策的事物人们往往会采纳延迟决策的策略。针对不同实际决策问题,采用的策略和行动也会不尽相同。表1给出了10个不同管理背景下所制定的策略和行动。 表1 不同管理背景下所制定的策略和行动 可以看到,不同的管理背景会导致不同的策略和行动,这也赋予了TAO模型更广阔的应用前景。 问题3其重点和难点在于如何构造科学合理的评价标准,常用的评价方法是多属性决策或多目标决策,用以对决策对象进行排序或评估。 定义2假设U是一个有限非空的论域,(L,⪯)是一个全序集合,C={c1,c2,…,cm}是评价集,它由m个评价属性构成,vci:U→L定义了在属性ci下的评价函数值,1≤i≤m。则∀x∈U,其总体评价函数可定义为: v(x)=wc1vc1(x)+wc2vc2(x)+…+ wcmvcm(x) (5) 为了更加清楚地解释定义2,本文以高考为例,假设M和N代表一本线和二本线。对于某一考生,高考成绩大于等于一本线可以报考一本大学;在一本线和二本线之间可以选择二本大学;小于二本线就只能选择专科或职业学院。最终,不同考生考取不同大学就是结果;而造成不同结果的原因是高考分数保证了评价标准的合理有效性。此外,除了多属性决策以外,多目标决策也是管理决策常用的评价方法。 定义3假设U是一个有限非空的论域,U=U1∪U2∪U3;R1(α,β),R2(α,β)和R3(α,β)代表3个决策区域U1、U2和U3所产生的决策风险,则总体决策风险可表示为: R(α,β)=aR1(α,β)+bR2(α,β)+ cR3(α,β) (6) 其中,a,b和c为R1(α,β),R2(α,β)和R3(α,β)所对应的风险系数,三支多目标决策的任务是选取合适的阈值α和β,使得总体决策风险最小 (7) 在公式(7)中,R1(α,β),R2(α,β)和R3(α,β)可看为是目标函数的3个子目标,α和β的最终取值是通过目标函数和约束条件构建相应的数学优化模型而求解得到的。一般而言,目标函数中的各子目标之间往往呈现出“此消彼长”的情况,设计相应的启发式算法去搜索全局最优解是求解多目标决策问题的关键。值得一提的是,多属性决策和多目标决策都属于多准则决策。在很多实际管理问题中,由于评价指标分为效益型、成本型、中间型,在目标函数中除了最小总体决策风险外,还存在最大决策效用、最大决策利润、最小决策成本等其他形式。在约束条件和决策排序中,各评价指标也需要进行相应的标准化和统一化处理。 决策分析是管理科学研究中的一门重要学科,多准则决策作为决策分析的一个重要分支,可根据决策方案是有限还是无限,分为多属性决策和多目标决策两大类。常见的决策分析方法,诸如AHP法、DEA法、TOPSIS法、PROMETHEE法、ELECTRE法等,很好地解决了实际决策中的分类问题、选择问题、排序问题和综合评价问题,能够积极推动管理决策研究领域的发展。 众所周知,在决策分析研究领域最经典的理论是Von Neumann和Morgenstern提出的期望效用函数理论(expected utility theory,EUT),该理论描述了理性人在风险条件下的决策行为,建立了不确定条件下对理性人的选择进行分析的框架。后来,Arrow和Debreu将其吸收进Walrasian均衡框架中,使之成为处理不确定性决策问题的分析范式。 定义4假设某个随机变量X以概率pi取值xi(i=1, 2, …,n), 而决策者在确定得到xi时的效用为u(xi)。 那么, 该随机变量X的总体效用可写为 u(x1)p1+u(x2)p2+…+u(xn)pn (8) 其中,X表示所研究的某个对象或事件,u(xi)表示第i种情况发生时的效用函数,pi表示出现第i种情况发生的概率。特别地,如果pi看为是属性权重,u(xi)看为是属性评价函数取值,则定义4退化为定义2的情形。 显而易见地, 将效用函数引入三支决策即需要改写公式(4)中的损失函数为效用函数, 则采取aP,aB,aN3种行动的总期望效用可分别改写为: (9) 与期望损失最小目标相反,效用函数理论是以最大效用为决策目标的。同样地,可以得到如下的3条决策规则: (P′):Φ(aP|[x])≥Φ(aB|[x])且Φ(aP|[x])≥Φ(aN|[x])同时成立,则x∈POS(X); (B′):Φ(aB|[x])≥Φ(aP|[x])且Φ(aB|[x])≥Φ(aN|[x])同时成立,则x∈BND(X); (N′):Φ(aN|[x])≥Φ(aP|[x])且Φ(aN|[x])≥Φ(aB|[x])同时成立,则x∈NEG(X)。 由于Pr(X|[x])+Pr(X|[x])=1,规则(P′)~(N′)只与条件概率Pr(X|[x])和效用函数u··(·=P,B,N)有关。此外,假设效用函数间大小关系满足uPP≥uBP>uNP和uNN≥uBN>uPN。将条件概率关系和效用函数关系代入到公式(9)中,则决策规则(P′)~(N′)可改写为: (P1′):如果Pr(X|[x])≥αu,则x∈POS(X); (B1′):如果βu (N1′):如果Pr(X|[x])≤βu,则x∈NEG(X)。 值得一提的是,在很多实际管理问题中,效用函数的表示可以多种多样,比如在产品销售问题中追求利润最大化;项目施工问题中的成本最小化;故障诊断问题中的风险最小化等。此外,很多问题具有多个决策目标,比如路径规划中的最小费用最大流问题、金融投资中的最大收益最小风险问题、分类问题中的最大精度最小代价问题等。进一步地,还可以考虑不同决策者的风险偏好问题。这需要在具体决策分析过程中灵活处理、活学活用。 期望效用函数理论的重要假设是决策者是理性人。然而,很多心理行为学和实验经济学研究表明:决策者在实际决策过程中不会完全理性,会受到人的复杂心理机制的影响。为了改进传统决策理论“理性人”假设,一系列行为决策理论和方法先后被提出,这里面最具代表性的是前景理论和后悔理论。 前景理论(prospect theory)是Kahneman和Tversky于1979年通过大量社会学和心理学实验而提出的一种行为决策理论[40],着重从人的心理特质、行为特征来揭示决策者的选择行为。前景理论的基本假设为:人在决策时会在心里预设一个参考点,对于高于参考点的收益型结果,人们往往表现出风险厌恶,趋于选择确定性收益;对于低于参考点的损失型结果,人们又表现出风险喜好,趋于选择风险性收益。 (10) 其中,φ和φ表示敏感性递减系数,κ为损失厌恶系数,它们满足0<φ,φ<1,κ>1。Kahneman和Tversky通过大量的心理学实验给出了上述参数的一组参考取值为φ=φ=0.88,κ=2.25[41]。 对于权重函数,前景理论会对小概率情形反应过度(overweighting),而对大概率情形则估计不足(underweighting),这在数学上呈现出一个非线性函数,用以刻画真实心理反应。为了方便起见,记π+(p(Δωi))和π-(p(Δωi))分别为收益型和损失型情形下的权重,则可以定义权重函数π(pi)为 π(pi)= (11) 其中,σ和δ分别表示收益型和损失型情形下反应过度和估计不足的影响程度,它们满足0<σ, δ<1。基于上述分析,对于某一对象或事件x,可以计算其前景值为 (12) 显而易见地,如果将公式(8)中的pi和u(xi)替换为公式(12)中π(pi)和v(Δωi),据此可以构建前景理论下的三支决策模型,文献[12,15,16]给出了具体的模型和方法。 与前景理论类似,后悔理论(regret theory)着重探讨决策者在决策过程中常出现后悔的心理状态,是由Bell、Loomes和Sugden在1982年同时提出的,它能够很好地描述个体在风险决策环境下的后悔和喜悦情绪[42-43]。在后悔理论中,假设x和y表示两个对象或事件。基于期望效用函数理论,Bell定义了选择x的效用为 v(x,y)=u(x)+R(u(x)-u(y)) (13) 其中,u(x)表示选择x的直接效用,R(u(x)-u(y))刻画了选择x而不选择y所带来后悔值形成的间接效用。令Δu=u(x)-u(y),R(Δu)>0表示喜悦值,R(Δu)<0表示后悔值。进一步地,直接效用u(x)和间接效用R(Δu)可分别构造如下: (14) 其中,θ为风险规避参数,τ为后悔规避参数。它们满足θ≥0,τ≥0。一般地,可以把后悔理论推广到多个对象或事件的决策问题中,公式(13)可以改写为 v(x,x*)=u(x)+R(u(x)-u(x*)) (15) 其中,x*表示所有选择方案中的最优方案。此时,选取其他方案都会后悔,此时有R(Δu)≤0。 显而易见,如果将公式(8)中的u(xi)替换为公式(13)的v(x,y),据此可以构建后悔理论下的三支决策模型,文献[13,17]给出了具体的模型和方法。 在前面的分析中,讨论了静态决策环境下的三支决策方法。在本小节里,主要探讨动态决策环境下的序贯三支决策模型与方法。 (16) (17) 假设Ω={X,X}表示事件的两种不同的状态,Α={aP,aB,aN}表示接受、延迟和拒绝3种决策策略。考虑到采取不同行动会产生不同的损失,记和分别表示第t时刻,当x∈X和x∉X时,采取3种不同行动的损失函数。则采取aP,aB和aN3种行动下的总期望损失可分别表示为: (18) 根据贝叶斯决策准则,可以选择总期望损失最小的行动集作为最佳行动方案,从而得到下面3条决策规则: (P″): Rt(aP|[x])≤Rt(aB|[x])且Rt(aP|[x])≤Rt(aN|[x])同时成立,则x∈POSt(X); (B″): Rt(aB|[x])≤Rt(aP|[x])且Rt(aB|[x])≤Rt(aN|[x])同时成立,则x∈BNDt(X); (N″): Rt(aN|[x])≤Rt(aP|[x])且Rt(aN|[x])≤Rt(aB|[x])同时成立,则x∈NEGt(X)。 由于Prt(X|[x])+Prt(X|[x])=1, 规则(P″)~(N″)只与第t时刻条件概率Prt(X|[x])和损失函数有关。 假设损失函数间大小关系满足:和将条件概率关系和损失函数关系代入到式(18)中,可得到序贯决策规则(P1″)~(N1″): (P1″):如果Prt(X|[x])≥αt,则x∈POSt(X); (B1″):如果βt (N1″):如果Prt(X|[x])≤βt,则x∈NEGt(X)。 对于第一种情况,假设POSt(X)、BNDt(X)和NEGt(X)分别表示第t时刻所对应的正域、边界域和负域。假设随着时间t变化,如果阈值αt满足:α1≥…≥αt≥αt+1≥…≥αT,则随着时间变化,正域逐渐增大,即:POSt(X)⊆POSt+1(X)。 对于第二种情况,如果阈值αt和βt满足βT≤…≤βt≤…≤β1<α1≤…≤αt≤…≤αT,则随着时间变化,正域和负域逐渐增大,而边界域逐渐减小。此时有: POSt(X)⊆POSt+1(X) NEGt(X)⊆NEGt+1(X) BNDt+1(X)⊆BNDt(X) 可以看到,上面两种情形下决策区域的变化也正好对应了粒计算理论中的多粒度层次变化情形,每一时刻对应某一粒度,这自然形成一种多层次的粒结构。在第一种情况下,随着粒度增加,正域增大,能够获取的有用知识和正规则也随之增加;在第二种情况下,随着粒度增加,边界域减少,相应的不确定性知识也随之减少。对于一个实际管理决策问题,可以建立合理的粒层选择机制和制定相应的最优粒度终止条件,来解决相关的选择、排序、评估和评价问题。 进一步地,如果同时考虑决策过程中时间和空间属性,可以构建三支决策的时空模型[44-45]。在时间属性下,三支决策模型主要考虑时间变化下,实时性、多次性、序贯性的决策问题;在空间属性下,三支决策模型主要考虑在信息粒化过程中,最优粒层和粒度的选择问题。显而易见,粒计算的相关理论和方法可以很好地解决序贯三支决策和时空三支决策问题。 自从三支决策相关理论与方法被提出以来,经过多年的发展,已经成为一种粒计算研究代表性理论和重要的不确定性知识发现方法。为了更好地整理和分析三支决策已有研究成果和后续研究方向,Yang和Li利用复杂网络对ISI Web of Science数据库进行分析,给出了三支决策领域的代表性研究团队、代表性学者和代表作信息,以及主要研究领域和方向[46]。Liu、Yang和Li梳理了三支决策与粗糙集理论的历史脉络、内在联系和相互关系,提出了一个基于三支决策的粒计算研究框架模型[47]。曹雯和梁德翠详细介绍了三支决策的背景及基本理论模型,对三支决策未来研究方向进行了展望[48]。刘盾等提出了广义三支决策与狭义三支决策理论[49]。Zhang等提出了基于效用函数的三支决策粗糙集模型和基于惩罚函数的序贯三支决策模型[50-51]。Jia等给出了一种新的多属性三支决策模型[52]。Yao等构建了基于3层分析和形式概念分析的三支决策理论体系[53-54]。此外,通过查阅国家自然基金管理信息系统,以三支决策为关键词,可以查询到该研究方向近年来的基金立项情况。表2列出了2015—2020年数学学部、信息学部和管理学部在三支决策研究领域获批的25项基金的详细信息。 表2 三支决策领域获批国家自然基金信息(2015—2020)Tab.2 The approved National Natural Science Foundations of China on three-way decision (2015—2020) 通过表2和前面分析可以看出,三支决策的研究呈现出两大特征:一是从狭义三支决策研究扩展到广义三支决策研究,并注重语义分析和实际意义;二是从单学科研究扩展到多学科研究,并注重多学科交叉和跨学科融合。就管理科学而言,如何将三支决策与实际问题有机结合,去更好地解决不确定性决策、群决策、序贯决策、决策与博弈、评估与预测问题,是三支决策未来的研究方向。 本文主要从管理研究视角出发,总结和分析了三支决策在管理领域的研究工作。首先,借鉴中国传统文化和经典典故,阐明了三支决策的哲学和管理思想;其次,从如何三分、如何行动、如何评价三个方面出发,剖析了三支决策TAO模型;再者,分别从行为三支和动态三支决策观点出发,讨论了效用三支决策模型、前景三支决策模型、后悔三支决策模型和序贯三支决策模型;最后,通过分析已有综述文献和国家自然基金资助情况,给出了三支决策未来的研究方向。虽然三支决策近年来在理论、方法、算法和应用上取得了很大研究进展,但还有很多问题值得深入研究。特别是近年来,随着人工智能和认知科学的兴起,三支决策已在大数据分析、知识发现、计算智能、智能信息处理等方面发挥越来越重要的作用,而基于认知计算的三支决策理论和基于可解释性的三支决策方法将会成为三支决策研究领域未来重要的发展方向。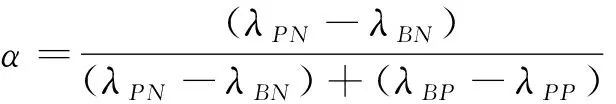
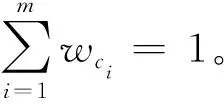
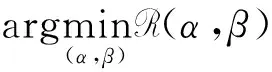
3 效用三支决策与行为三支决策
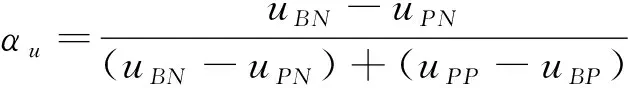
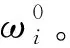
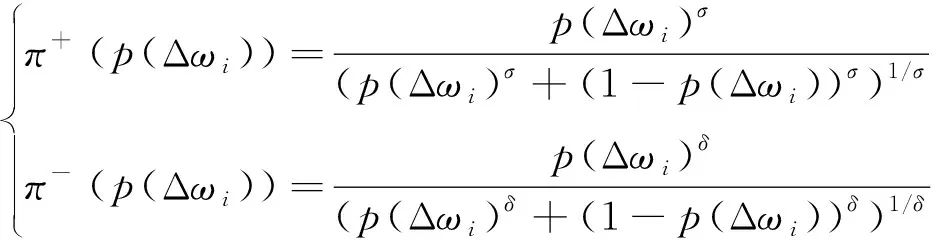
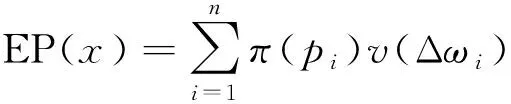
4 动态三支决策方法
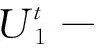
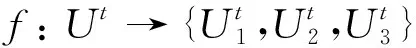
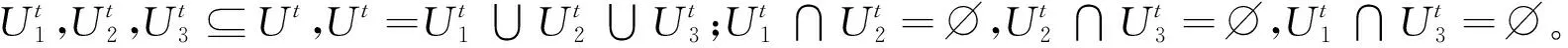
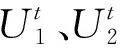
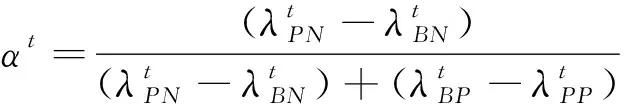
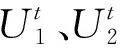
5 三支决策未来研究方向
6 结语
