一种用于三电平能馈逆变器的改进型特定次谐波消除脉宽调制算法

吴雪峰，陈洁莲，王 雄，宋乾儒，尹维恒

（株洲中车时代电气股份有限公司，湖南 株洲 412001）

0 引言

中点箝位(neutral point clamped，NPC)型三电平拓扑是当前应用最广泛的多电平拓扑[1-4]。相比传统的两电平变流器，三电平NPC 变流器具有输出功率大、输出波形总畸变率(total harmonic distortion，THD)小、器件电压应力和系统电磁干扰低等优点[5]，被广泛应用于中高压变频调速、有源电力滤波和电力系统无功补偿等领域。

在城轨再生制动能量回馈领域，能馈逆变器的主要特点是高电压、大电流、大功率，这使其最高开关频率受到散热系统的限制[1]。在实际应用中，针对在开关频率较低即在低载波比工况下的调制方式，如果采用传统脉宽调制方法，则需要庞大的滤波装置以满足系统对谐波限制的要求，这势必造成逆变器体积庞大而笨重，大大提高了逆变器的成本[2]。特定次谐波消除调制方式（selected harmonic elimination PWM,SHEPWM）是目前在大功率逆变系统中被广泛应用的一种方法。相比正弦脉宽调制（sinusoidal PWM,SPWM）技术，SHEPWM技术具有开关频率低、无特定低次谐波、输出波形质量高、开关损耗低、转换效率高等特点[3]。SHEPWM技术并不能减小逆变器输出电压波形的总谐波失真（THD），而只是改变各次谐波的分布，选择性地消除对电气设备和外部线路影响较大的低次谐波，其代价是不可控的高次谐波畸变将增大。在SHEPWM方式下，会出现不可控的谐波幅值很大的现象，甚至导致电压THD大于同等开关频率下SPWM方式的，这就背离了应用SHEPWM技术的初衷[6-8]。另外，由于特定消谐技术需要求解一组非线性的超越方程组，其求解较为困难且过程复杂，故传统上常采用牛顿迭代法，而初值给定方法是影响牛顿法求解速度和敛散性的关键因素之一，即开关角度求解难度很大程度上依赖于初值选取合适与否[1,5]。

本文在对SHEPWM算法深入分析的基础上，提出一种改善输出电压谐波分布、降低剩余谐波峰值且可以不依赖初值选取的SHEPWM开关角求解方法[9]。该方法主要通过优化SHEPWM数学模型，不再令求解的低次谐波幅值为零，而是引入一组相对误差值，在求解方程中将工程上可以接受的低次谐波幅值带入方程组，从而可以改善输出电压分布，综合降低THD。求解过程中引入多目标遗传算法，可以求解出在多个约束条件下的非线性超越方程组的最优解，避免了牛顿迭代法中对初值依赖的问题。最后通过仿真对比分析了改进型SHEPWM算法与基于传统数值算法的SHEPWM的谐波含量，结果证明了所提改进型SHEPWM 优化算法的优越性[10]。

1 NPC三电平能馈逆变器消谐模型分析

三电平能馈逆变器采用二极管箝位式结构，能馈逆变系统如图1所示，其主要由三电平NPC逆变器、LCL滤波器和三相交流电网组成[11]。

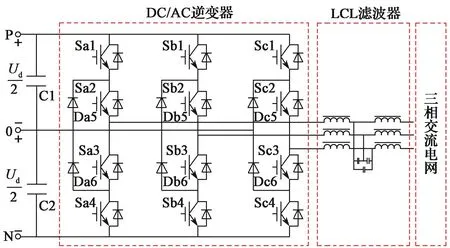
图1 能馈逆变系统Fig. 1 Energy feedback inverter system

以三电平单相相电压分析为例，相电压波形在半周期内，开关角的个数有偶数和奇数两种情况：当k（开关角度个数）为偶数时，相电压波形如图2所示；当k为奇数时，相电压波形如图3所示。图中，Ud为直流电压；α为开关角；ω为傅里叶分解频率。

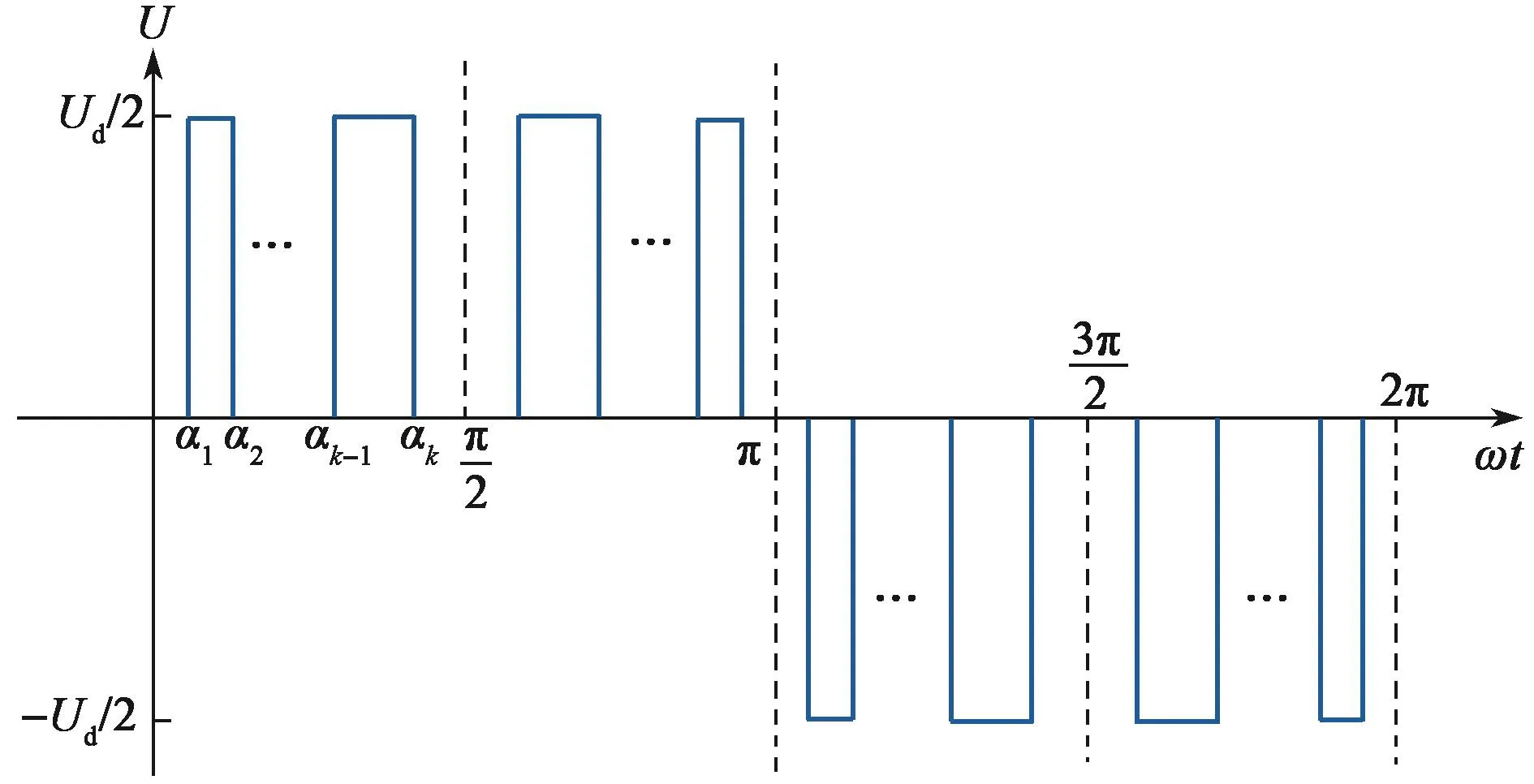
图2 NPC三电平逆变器相电压波形（k为偶数）Fig. 2 Phase voltage waveform of NPC three-level inverter（k is even）

图3 NPC三电平逆变器相电压波形（k为奇数）Fig. 3 Phase voltage waveform of NPC three-level inverter（k is odd）

其电压波形的傅里叶级数可以表示为

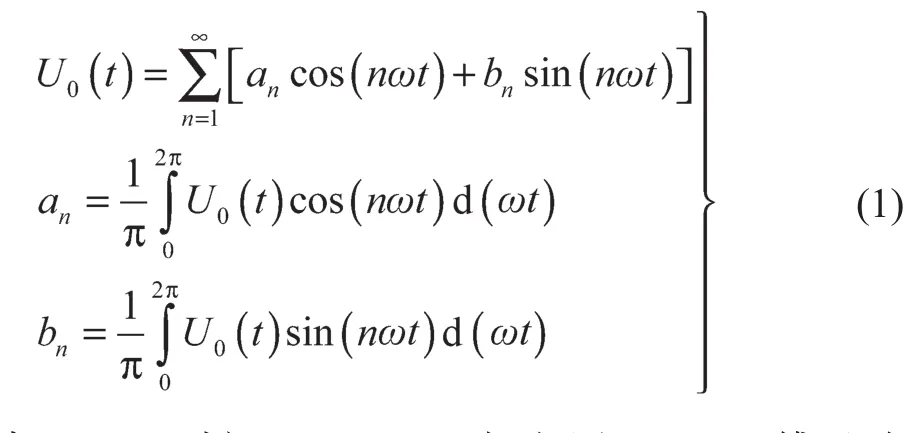
式中：t——时间；U0(t)——相电压；an——傅里叶级数中余弦项系数；bn——傅里叶级数中正弦项系数；n——基波和各次谐波次数。

在三相对称电路里，相电压中的3次谐波及3的整数倍次谐波在线电压中相互抵消，因此波形可被简化为

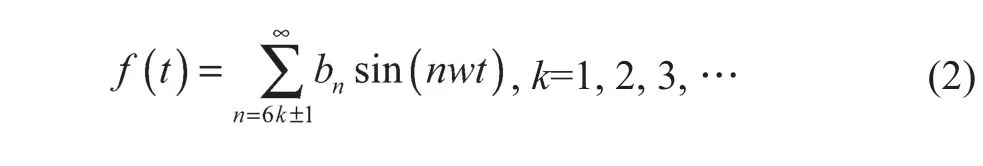
为简化计算，输出波形应能满足1/4周期对称，即半周期的镜像对称，则可消除傅里叶级数中的偶次谐波；同时在半周期内以π/2为奇对称，即可以消除谐波中的余弦项，因此an=0，求解该傅里叶级数的系数bn并简化，可得到

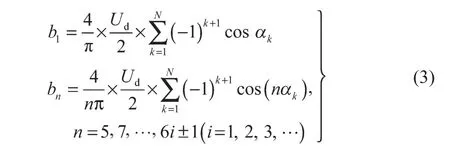
令b1=mUd（基波分量），其中，m为调制比，即调制深度；令其他(N-1)个谐波的幅值为零，则有

定义调制比为逆变器输出相电压基波幅值与直流母线电压一半的比值，即

联立式(3) ～式(5)，构成N个未知数的N维方程组。解此方程组，得到一组在[0, π/2]内的脉冲开关角，进而可以得到整个周期内的开关角，则可以实现N个指定阶次的谐波幅值为零。联立方程，化简后可得

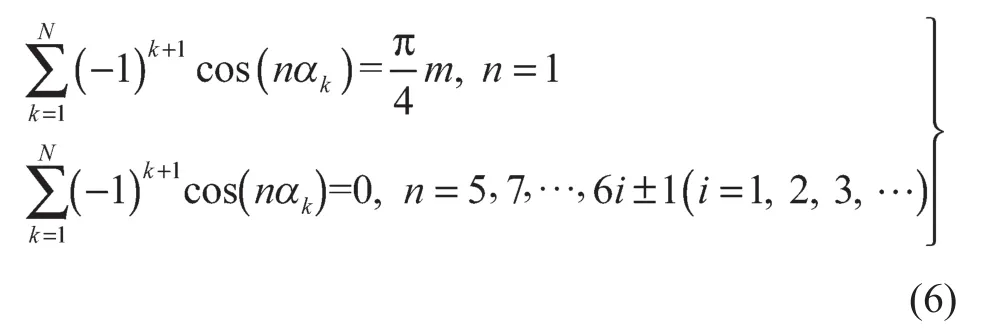
式(6)所示的方程组构造了在1/4 周期内用N个开关角度来消除(N-1)个特定谐波的特定消谐技术的传统数学模型。其是一个非线性超越方程组，求解难度直接制约了SHEPWM技术的应用，通常需要采用牛顿迭代法进行求解，因此求解问题被转化为如何得出比较好的初始值问题。

2 遗传算法及优化数学模型建立

传统三电平NPC逆变器SHEPWM调制算法有两个局限性：

（1）采用迭代求解或试凑等方法寻找初始值,对初值依赖程度大；

（2）不可控制的高次谐波畸变增大，在SHEPWM调制方式下，甚至会出现不可控的谐波幅值很大现象，导致THD大于同等开关频率SPWM调制方式下的。

针对传统三电平逆变器SHEPWM消谐的弊端，本文提出一种最优谐波分布SHEPWM开关角的数学模型及求解方法。该方法可以克服传统牛顿迭代法的依赖初值选取问题，大大简化烦琐的初值试凑过程，提高求解方法的普适性；并能克服传统特定消谐PWM技术不可控的高次谐波畸变增大的问题，在低次谐波消除到满足工程要求的情况下，通过降低高次谐波的幅值以降低总THD。

遗传算法被广泛应用于函数优化、寻优处理等方面，将遗传算法引入电力电子控制方面，可提供一种解决复杂、非线性的功率变换器开关角度求解的新方法。

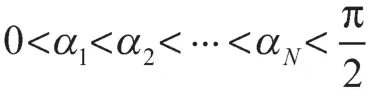
式中：y0(α)——基波函数；y1(α),y2(α), …,y(6i-1)(α)——各次受控谐波函数；ξ1,ξ2, …,ξ(2i-1)——确定的误差值，其定义为各次谐波幅值相对于基波幅值的比例。

采用遗传算法的具体设计过程如下：

（1）编码。采用二进制编码,每个开关角由二进制数编码表示。

（2）编写适应度函数与目标函数。适应度函数为

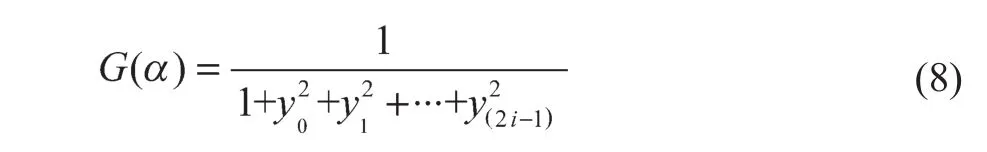
目标函数如下：

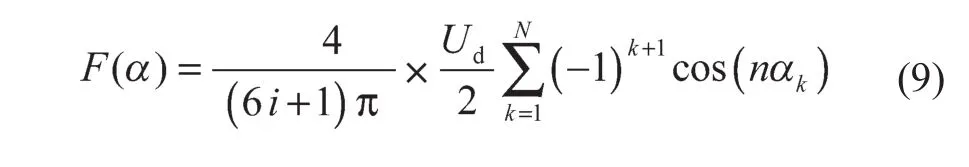
利用遗传算法全局寻优就是在满足个体适应度最大的同时，能够实现种群（各个要求解的开关角度）F(α)最小。这样，在保证可以把可控的低次谐波含量消除到工程上能够接受的规定幅值以下的同时，也能降低不可控制的谐波幅值；此外，利用遗传算法求解开关角度过程中，可以不受开关角度初值选取的限制。

（4）交叉操作策略。采用单点交叉，两个个体交叉时在该点位置上进行互换，生成两个新个体。

（5）变异操作策略。变异操作就是按照一定的概率随机改变染色体中基因的取值。对二进制编码而言,就是将所选染色体中的基因值取反，即1变0，0变 1。

按照上述遗传算法进行全局寻优，以N=16为例，

其目标函数为

适应度函数为

其中：

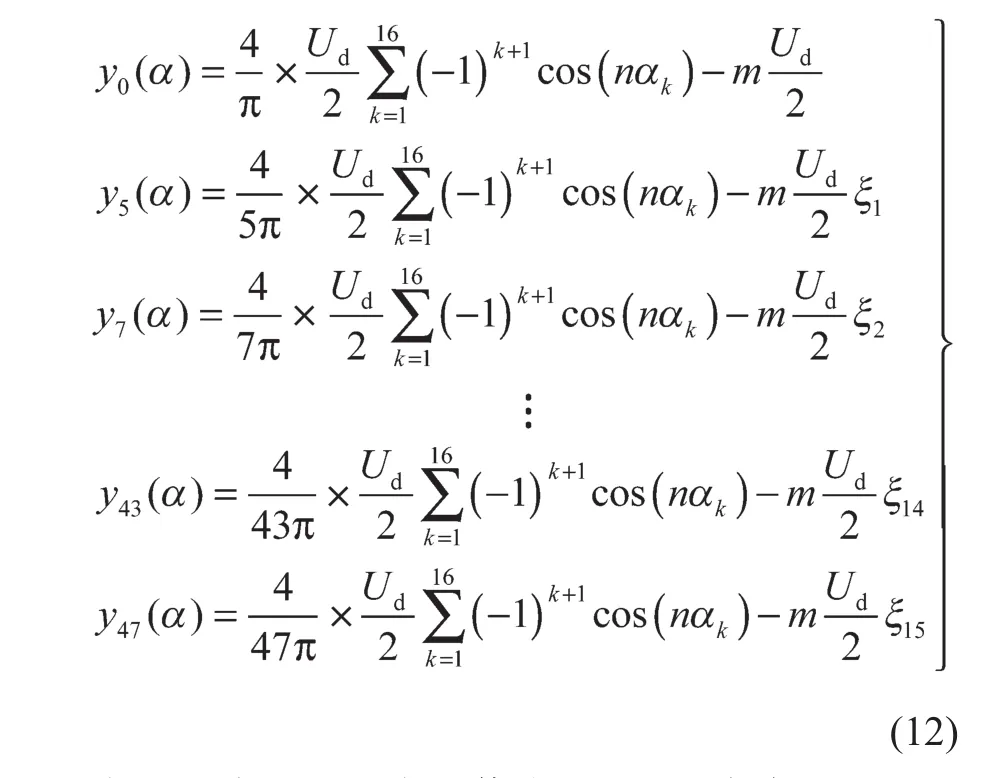
式(12)中，m最大取值为1.15；根据标准GB/T 14549-1993《电能质量 公用电网谐波》规定的允许谐波范围，为使谐波幅值小于基波幅值的1/1000～1/500，ξi值的选取可依经验和需要适当放宽。

取m= 0.8，令ξ1= 0.05，ξ2= 0.035，ξ3= 0.03，ξ4=0.03，并令ξ5, …,ξ15都为零。即允许5, 7, 11, 13次谐波幅值可以不为零；而大于13次、小于47次的谐波幅值为零，则可以将式(12)变换为

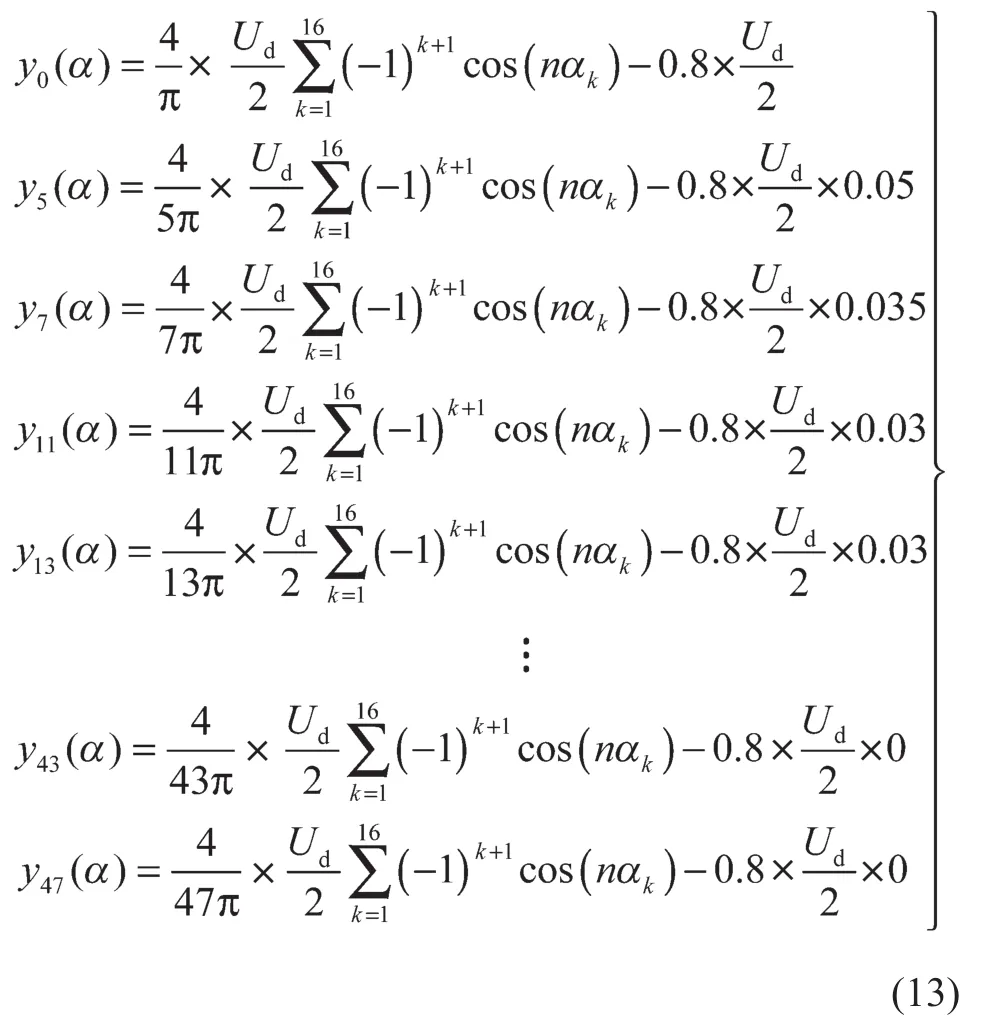
本文在满足允许误差为10-20(可以根据精度要求调整)前提下，以可控的某些低次谐波畸变不为零为代价来换取总的THD的减小，以获得更好的谐波特性。

此外，由数学推导可知，式(7)中的各项连续可微，所以方程组解的轨迹也是连续的，即开关角度的轨迹是连续的。因此，在遗传算法求解的过程中，可以得到一组满足上述约束条件下的角度值。例如，在求得出m=mi解的基础上，给m一个很小的增量dm。由于开关角度轨迹的连续性，通过这种方法可以大大地减少调制比为m=mi+dm时计算出符合要求的目标个体所需要的迭代次数，从而在很大程度上提高了遗传算法的效率。如此逐步增大m，可以得到m全范围内的解。因此，在THD降低的情况下，得到一组m全范围内开关角度的轨迹（图4）。

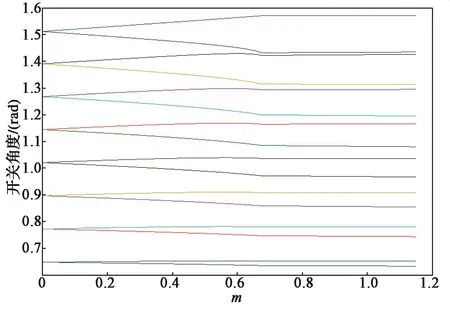
图4 求解的开关角度Fig. 4 Switch angles of solution

如图4所示，横坐标为0 ～ 1.15的调制比，纵坐标为16个开关角度的轨迹。可以看出，随着调制比变化，开关角度的轨迹是连续的。

3 仿真结果

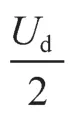
为进一步验证改进型SHEPWM算法的有效性，在相同工况下，对采用传统数值法求解的SHEPWM算法和本文的改进型SHEPWM算法进行仿真分析对比，仿真结果如图6所示。可以看出：

（1）传统SHEPWM能将低次谐波消除为零，但是因为其对不可控的高次谐波没有限制，造成不可控制的谐波第一个峰值达到很高的幅值，如图6中，传统SHEPWM线电压的THD为56.49%，大于改进型的SHEPWM的55.85%（图5），使得总的THD反而会升高。

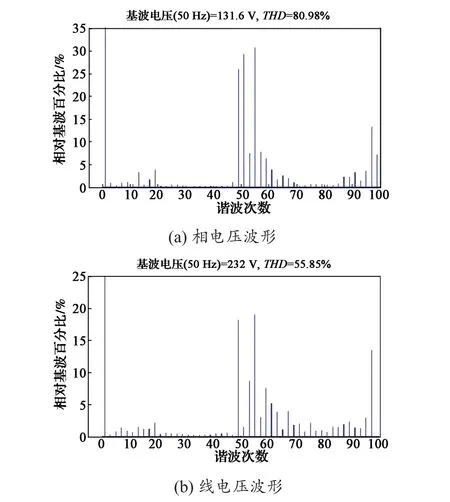
图5 NPC三电平逆变器SHEPWM仿真波形（m=0.8）Fig. 5 SHEPWM simulation waveform of NPC three-level inverter（m = 0.8）

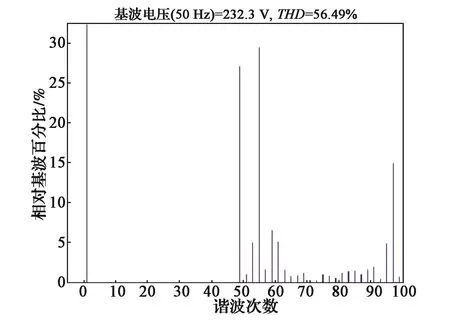
图6 传统SHEPWM算法线电压波形Fig. 6 Line voltage waveform of traditional SHEPWM algorithm

（2）改进型SHEPWM算法应用在三电平NPC逆变器后，使总谐波畸变率得到了降低。以将低次谐波幅值限制在允许值范围内作为代价，将高次谐波幅值变小，来改善输出电压谐波分布，同时使得不可控的电压谐波幅值受到约束而得以降低，从而提高输出电能质量。仿真结果进一步证明了本文提出的改进方法切实有效。

4 结语

本文提出一种改进型SHEPWM调制算法，较传统SHEPWM调制算法，其能够有效减少三电平NPC逆变器的输出电压谐波量，提高逆变器并网的电能质量，减少对电网的谐波污染。该改进型SHEPWM调制算法由于引入遗传算法，大大简化了烦琐的初值试凑的过程；并通过优化建模，克服了SHEPWM技术中不可控的高次谐波畸变增大的问题，降低了输出电压的谐波畸变率。

本文仅定性分析了适当提高低频谐波含量以综合改善高频谐波分布问题，并未进一步定量分析保留低频含量与改善高频谐波分布之间的定量关系，这将是后续进一步研究的方向。