地质矿物样品化验误差处理方法研究

王晓东

（甘肃省有色金属地质勘查局张掖矿产勘查院测试中心，甘肃 张掖 734000）

在矿山地质勘测工作中，对于所开采的矿物样本作出化验是基本且关键的一个环节，主要是对矿物样本中的金属元素作出检测，以此来确定矿产的属性与使用范围。传统的检测方法沿用时间较久，虽然可以获取预期的检测结果，但是在实际应用的过程中依然会存在误差和缺陷，对于最终的检测结果造成影响，面对这种情况，需要对化验过程中出现的误差进行处理，确保化验结果的真实可靠性。

其实，矿石样品化验误差的相关分析通常是判定矿产质量以及属性的重要途径，在矿山勘探中占据主要地位。通过对矿石样品中的金属元素绝对误差和相对误差对比，再加之误差允许标准的判定，得出样本的最终评价，以此来判断矿石的品位信息以及储量值的计算。通常情况下，对矿石样本进行化验，并处理出现的误差是一项十分繁琐且庞大的工作，主要是因为矿石的样品获取需要在不同的区域提取，而样品化验一旦重新进行就会造成大量的资源浪费以及返工浪费[1]。所以，最近几年，我国在矿物样品化验误差处理方面投入了大量的人力物力财力，立志于实现高效率、高质量的化验工作，最大程度地降低存在的误差[2]。因此，对地质矿物样品化验误差处理方法进行研究，在较为真实的环境之中，在矿石样本中提取相关的金属元素，例如：金、银、铜、铅、锌、钨等，利用科学的仪器和设备获取具体的数据信息，在化验的过程中，对各个环节加强控制，以此来降低误差，提升我国矿产品化验误差处理的综合水平[3]。

1 地质矿物样品化验误差处理方法设计

1.1 确定样品的平均误差极值

在对地质矿物样品化验误差处理方法进行设计前，需要先确定样品的平均误差极值。误差极值指的是在化验的过程中，允许出现的最大误差，一旦超出这个范围，则表明测量化验出来的结果相对不准确，可靠性较低。需要计算出平均误差极值，将其作为测量化验的标准，对误差进行控制。获取矿物样品，并确保矿石处于同一个高度内，利用无杂质的水清洁矿石样本，去除相应的杂质，将石块放置在溶液之中，进行化学浸泡，此步骤是为了去除矿产样品内部的杂质，使其处于单一介质的状态，在化验的过程中也可以更加精准、顺利一些。将矿石样品进行密封处理，静置大概24h之后，取出风干，等待化验。

在化验之前，通过专业的测量工具或者设备对样品属性以及内部所含元素进行测量，通常情况下，矿石中会含有一些金属元素，例如：铜、铁、金、银等，这些元素需要对其作出特殊的处理，一旦处理不当，便会对化验结果造成影响。不仅如此，在实际的处理过程中，还需要将多余的元素进行剔除，以此来避免出现化验误差。当然，提出外部元素的方法也有很多，应用最为广泛的大致可以分为以下几种：化学法、物理法以及复合强效消解法。化学法通常情况下，是利用与元素呈相反特性的另一种化学元素来营造相互抵消的处理环境，同时，在处理的过程中，可以最大程度地降低存在的误差；物理法与复合强效消解法主要是采用高温或者低温的方式来对矿物样品进行化验，最终得出预期的处理结果。完成元素剔除处理后，接下来，通过测量出的数据信息，首先需要计算样品中各个元素的品位，具体如下公式1所示：

公式1中：F表示各个元素的品位占比，D表示实测均值，V表示元素的单个数值，ℑ表示极值误差。通过以上计算，最终可以得出实际的元素品位占比。以此来确定相应的化验百分比，通过不同的种类将样本划分为不同的区域，测量随机误差，并在此基础上计算平均误差极值，如下公式2所示：

公式2中：M表示平均误差极值，F表示各个元素的品位占比，ℵ表示元素的单个误差。通过以上计算，最终可以得出实际的平均误差极值，结合样品的实际变化情况，再加上元素的分解程度，采用比照的方式来验证得出的平均误差极值是否处于合理的范围之内，如果存在误差，则可以通过差值引入的方式来消除误差，并形成更为全面、系统、稳定的处理结构，为化验误差的实际处理奠定基础。

1.2 创建校正矿物样本误差处理模型

在完成样品的平均误差极值的确定之后，接下来，在以上基础中，创建具有校正能力的矿物样本误差处理模型。首先，利用以上所计算和测量的相关数值，计算样品的误差校正系数，如下公式3所示：

公式3中：G表示样品的误差校正系数，f表示实际校正距离，g表示误差距离，ω表示预估差值。通过以上计算，最终可以得出实际的误差校正系数。完成之后，利用其确定校正的实际范围，并设定校正的标准，如下表1所示。

表1 矿物样本误差校正标准表

根据表1中的数据信息，最终可以完成对矿区样本误差处理校正标准的设定。在此基础上，创建对应的体系，形成误差处理的模型。随后，将上述得出的数据信息汇总整合，添加在模型之中，进行初次的化验训练。但是训练的过程中，对于矿物样品的取样存在不同程度的差异，这也会导致在训练中时常会产生一定量的随机误差。这种随机误差通常是不可避免的，其没有规定的方式完全消除，仅可以尽量避免。所以，化验人员可以先在不同的区域分别获取对应的样品，随后，依据设定的标准，对样品进行化验前的处理，此时，应该尽量保持化验因素环境的高度统一，并排除外部因素带来的影响，尽量避免随机误差的出现。在模型中建立线性的对比结构，化验的过程中出现异常或者误差时，可以依据模型中固定的处理模式，及时对化验中样内部的物质以及金属元素进行识别，通过特殊的方法去除，尽量避免误差在此初出现，利用模型作出高效率，高质量的化验误差处理，进一步确保最终化验结果的准确性。

1.3 建立分离对比的回归直线误差处理矩阵

在完成校正矿物样本误差处理模型的创建之后，接下来，为了进一步完善优化误差处理模型的性能，需要同构分离对比的方式来建立回归直线处理矩阵，以此来进行更为细致的误差处理。此时，化验出现的误差通过模型的处理已经确定，并实现了初始的误差处理，通过上述测量的数据信息，再加之分离对比的方法，在模型中创建回归直线误差处理矩阵，如下公式4、5、6所示：

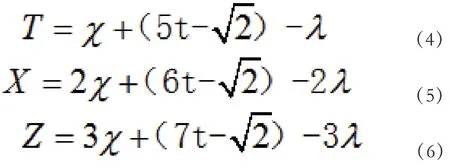
公式4、5、6中：T、X、Z表示回归处理系数，χ表示差值对比值，t表示直线处理范围，λ表示允许出现的极限误差值。通过以上计算，最终可以得出实际的回归处理系数，利用这个数值创建回归直线误差处理结构，并计算其实际的误差理范围，与原本的处理范围作出分离对比，范围较大的作为模的误差处理范围，如下公式7所示：

公式7中：H表示误差处理范围，γ表示直线处理百分比，h表示估算误差比例。此时，结合得出的是数据信息，进行分离对比处理标准的设定，具体如下表2所示。

表2 分离对比处理标准设定表

根据表1中的数据信息，最终可以完成对分离对比处理标准的设定。随后，依据上述设定的标准，对所测算完成的误差结果进行比照，如果存在较大的误差，会影响最终的化验结果，需要根据标准，进行对应的处理与调整，严重的甚至要重新取样，以确保化验结果的精准性。随后，在直线处理矩阵之中，将对应的化验处理范围扩大，同时，结合地质物样品的特征，完善相对应的处理结果，并进行对比。通过对比可知，本文所设计的回归直线误差处理范围较大，所以，作出分离融合，并将上述的范围设定在误差处理模型之中，使其在化验的过程中可以更加全面地随出现的误差作出处理，至此，便完成了分离对比的回归直线误差处理矩阵的创建。

1.4 重叠试剂作用法实现矿物样品化验误差的处理

在完成分离对比的回归直线误差处理矩阵的建立之后，此时，样品的误差已经得到了大幅度降低，并且进行了合理的误差处理，但是在化验的过程中，仍然存在问题和缺陷，需要通过试剂进行重叠作用，以此来确保最终测试结果的稳定可靠性。先利用相关的测量观察仪器对此批次的矿物样品作出一定的了解，如下图1所示。

图1 矿物样品观测图

通过图1，可以了解到此时矿物样品的相关化验情况。利用不同的实试剂将矿物样品重新去除杂质。以重叠的形式在化验以及误差处理模型中获取对应的数据结果，通过与前期化验的结果对比，最终可以得出存在的误差。结合上述测定化验的模型，对样品进行误差作出初始的预估。通常情况下，在测试处理过程中，对于误差的预估也需要依照对应的标准来执行。矿物质样品的处理与检验，相关的误差标准值也存在不同程度的差异，结合重叠误差作用法，先设定样品化验的处理范围，并计算允许出现的极限误差值，如果测试的误差值在所设定范围之内，表明对于最终的实验结果影响较小，反之，如果超出相应的范围，则代表实验结果的可靠性与真实性有所降低，存在不可信的风险。随后，结合得出的极限误差值，计算误差处理重叠数值，如下公式8所示：

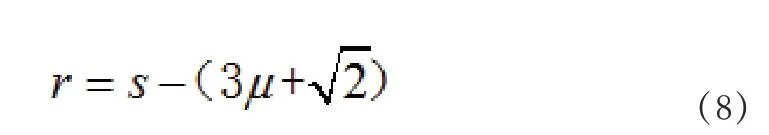
公式8中：r表示误差处理重叠数值，s表示重叠范围，µ表示品位系数，通过计算，将得出的误差处理重叠数值添加在模型之中，实现对出现误差的处理。但需要注意但是，根据得出的误差处理重叠数值可以设定出具体的重叠误差处理范围，在对样品化验的过程中，创建多目标的化验结构，与传统化验环节不同的是，此时创建的多目标化验结果是以阶段时化验为主要的方式，并且每一个阶段的化验结构也是独立的，通过设定化验的目标，结合处理流程，最终完成预期的测试任务。另外，为了降低随机误差度测试结果的影响，可以对相应的处理环节进行合理地简化，一定程度上可以降低出现误差的几率，同时在测定时，扩大延伸对应的化验范围，实现化验路径的创新，冲破传统化验方式的束缚，最终完成对化验误差的处理与控制。

2 方法测试

2.1 测试准备

本次测试主要是对地质矿物样品化验误差处理效果进行分析探讨，测试共分为两组，一组为传统的重叠误差处理方法，将其设定为传统重叠误差处理组；另一组为本文所设计的方法，将其设定为均值校正误差处理组。搭建测试环境。本次测试选取K矿场中的不同区域矿产物作为对象。准备处理试剂，如下：硫酸铜、高锰酸钾、试验用稀盐酸，测试允许出现的误差范围，相对误差为0.25～0.5之间，决定误差在0.11～0.135之间，元素的品位标准设定在1.9以下，根据以上数据信息，计算样品的实际平均品位，如下公式9所示：

公式9中：J表示样品的实际平均品位，表示均方差，s表示系统误差，β表示随机误差。通过以上计算，最终可以得出样品的实际平均品位。结合实际平均品位，设定出相应的品味化验处理测试模型。此模型的应用仅限于测试过程中。模型中的结构分别是独立交互的，虽然在单一任务目标的执行与处理上不具有任何的联系，但是在实际应用时，仍然具有一定的交互关系，此时，可以根据上述所计算获取的数据信息，设定化验误差的处理交互范围。

通常情况下，设定误差的极限值为5.25，但是由于此次是对地址矿物样品的化验，矿物的化学元素在不同的环境下会发生相应的变化，所以，在测试化验的过程之中，也极有可能会因为外部因素或者天气状况的影响而发生变化，进而产生对应的测定误差。而误差可能是随机误差、系统误差也有可能是粗大误差，均是较难控制的。所以，需要将将这个品位值作为误差处理的基础标准，在此基础上，计算误差极值范围，如下公式10所示：

公式10中：N表示计算误差极值范围，ℜ表示误差标准，c表示概率系数，J表示样品的实际平均品位。通过以上计算，最终可以得出实际的计算误差极值范围。所设定的范围之中，可以对上述的方法进行二次测试，以此来确保最终测结果的稳定性以及可信性，但是需要注意的是，测试的环境以及条件均是相同的，并且在所搭建的测试环境和应用数据信息中进行测试。使用两组方法同时进行，测试前核查相关的设备以及测量仪器，确保其处于稳定运行的状态，并不存在影响最终测试结果的外部因素，完成之后，开始测试。

2.2 测试过程及结果分析

在以上创建的测试环境中，进行地质矿物样品化验误差处理的测试，本次测试选取K矿场的矿石分析化验，需要先对矿石样本进行基础处理。在实验皿中倒入四分之一的硫酸铜溶液，和大约10ml的试验用蒸馏水，将矿石样本置于其中，静置20min，随后，取出样本，在处理皿中加入2g的高锰酸钾，并添加适量的淡盐水，大约5ml即可。将样本二次浸入处理溶液之中，去除其中的杂质，避免影响最终的测试结果。完成以上布置，进行化验误差的处理，具体的测试过程如下图2所示。

图2 化验误差的处理流程图

根据图2中的处理测试，可以得出相应的测试结果。进行两组测试，对两组测试结果进行对比分析，如下表3所示。

表3 矿产样本化验误差处理结果分析

通过表2中的数据信息，可以得出最终的结论：在相同的测试环境之中，对比于传统的重叠误差处理方法，本文所设计的误差处理方法得出的差值百分比相对更低，这表明其对于化验误差的处理效果较好，有效地降低了存在的误差，同时在测试的过程中，简化了具体的化验处理环节，将存在的化验误差降至最低，在合理的范围之内，不会对最终的测试结果产生较大的影响。确保了自重化验结果的可靠性，具有一定的实际应用价值。

3 结语

综上所述，便是对地质矿物样品化验误差处理方法的研究与分析。其实，矿产品的化验误差出现的原因主要是随机误差和系统误差。这两方面的问题可以通过加强相关的人员的专业素质，或者提升化验设备质量来避免。除此之外，就是完善优化对应的误差处理方法。这种形式更加全面，可以提高化验结果的精确度以及可靠性，对于矿石中的元素测量也更加准确，细化各个化验流程，尽量避免过程中出现误差，一旦出现，则通过科学的方法做出正确的处理，以此来提升结果的可靠性。