商用车循环球式EPS系统建模及仿真分析
2021-07-22马相飞张旭王印武星
马相飞,张旭,王印,武星
(陕西汽车集团有限责任公司,陕西 西安 710043)
引言
循环球式电动助力转向(EPS)是在当前商用车技术领域中日渐成熟且很有发展前途的动力转向系统。相较于传统的液压助力转向系统具有更高的经济型、安全性和操纵稳定性。同时,EPS可根据车速的高低来控制路感,解决转向系统“轻与灵”的矛盾,综合改善汽车转向系统的性能[1]。
1 系统模型
文章针对常用螺杆助力式循环球式EPS转向系统进行分析,该系统一般由控制系统和机械系统两部分组成,关键部件主要包括转向盘、转向轴、扭矩传感器、电动机、减速机构、ECU及循环球式动力转向机[1-2]。
为分析问题方便,将循环球式EPS系统简化为只包括转向盘和上端转向轴、助力电动机、下端转向轴三个电动助力转向系统的动力学模型,如图1所示。
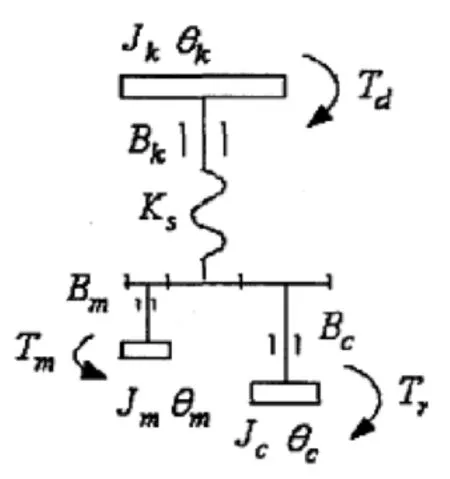
图1 转向系统结构图
1.1 转向系动力学模型
对转向盘和上端转向轴、下端转向轴分别进行动力学分析,可得到如下方程:

式中:Td为方向盘转矩,Ks为扭杆刚性系数,θk为方向盘转角,Bk为转向轴的黏性阻尼系数,Jk为转向盘转动惯量,Tr为转向轴的阻力矩,Ta为电机对转向轴的助力矩,Bc为前轮与转向机构等效转向轴的黏性阻尼系数,Jc为电机轴的转动惯量,θc为转向轴转角。
1.2 电动机模型
本文所研究循环球式EPS系统助力电机采用永磁无刷直流电机,其等效电路如图2所示:

图2 等效电路图

式中:U为电机端电压,L为电机电感,R为电枢电阻,Kb为反电动势系数,Ka为电机转矩系数,I为电机电流,Jm为电机的转动惯量,Bm为电机转轴的黏性阻尼系数,Gm为涡轮蜗杆速比。
1.3 车辆二自由度模型
为了便于分析 EPS 系统控制策略对汽车操纵稳定性的影响,将汽车简化成二自由度模型。该模型包括侧向平移运动和横摆运动。Fyf和Fyr分别表示前后轮侧向力,β表示车体侧偏角,δ为前轮转向角,lf和lr分别表示质心到前后轮的距离,横摆角为ωr,k1、k2为侧偏刚度,m是车辆的质量,v是车辆的速度,Iz是车辆横摆转动惯量[3]。模型如图3所示:

图3 二自由度自行车模型
简化后,得到模型的运动微分方程为:

2 循环球式EPS系统助力特性控制策略
EPS系统之所以能兼顾转向系统的轻便性与灵敏性,主要在于其助力特性是随车速及转向盘转矩的不同而改变的。而EPS助力转矩大小与直流电机成正比关系,故通常用电机电流、转向盘转矩和车速来表示助力特性。EPS的助力过程为控制器根据转向盘转矩及车速,通过模糊逻辑推理,确定电机的目标电流,然后通过控制电机电流实现目标转矩地输出[4]。
目前,PID控制算法因计算量小、实时性好、易于实现等特点被广泛用于循环球式EPS转向系统对助力电流的控制中。PID控制器通过对目标电流和实际电流之间的偏差进行调节,而后将调节出的控制电压通过PWM方式作用在助力电机上。其控制原理如式(8)所示,目标电流跟踪控制器如图4所示。

图4 模糊PID控制仿真框图
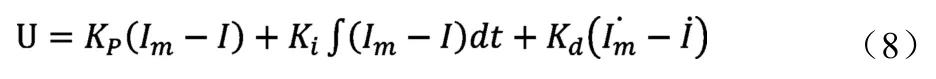
式中:Im为目标电流,KP、Ki、Kd为比例、积分、微分控制系数。
3 仿真结果及分析
根据第一节中推导的转向系统数学模型、电机数学模型、车辆二自由度数学模型,在Matlab/Simulink中搭建车辆循环球式电动助力系统的仿真模型,如图5所示。模型以方向盘转矩、车速作为输入,以车辆横摆角速度作为输出,模型采用的主要参数如表1所示。

表1 仿真主要参数
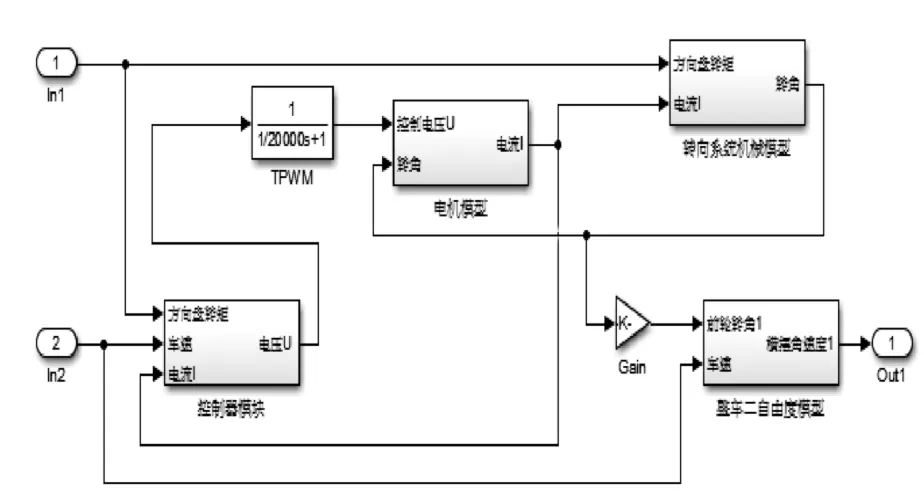
图5 车辆循环球式电动助力系统仿真框图
分析图6可以得出,在10s的仿真时间内,目标电流与电机电流曲线趋势保持一致,说明模糊PID控制器的跟踪误差能够在仿真时间内保持对目标电流的持续跟踪,实现对系统电流进行有效控制。图7是汽车未加载循环球式EPS下的车辆横摆角速度响应曲线,图8是汽车加载循环球式EPS后,基于PID控制器下的横摆角速度响应曲线,从图7及8可以看出,同一转向盘转矩阶跃输入下,加载助力的系统有较大的横摆角速度输出,且横摆角速度超调量由 87.5%降到了52%,说明其瞬态响应及转向盘力特性得到了一定程度的改善。

图6 电流跟踪图
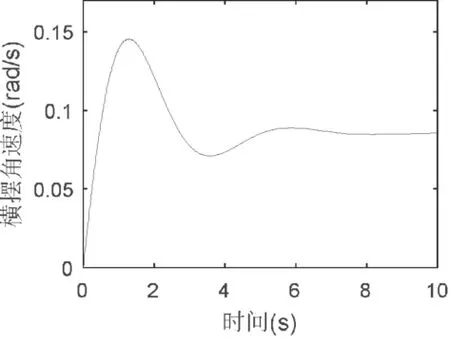
图7 未加载EPS横摆角速度

图8 加载EPS横摆角速度
4 结论
本文通过对转向系统机械模型、电机模型、控制模型及整车二自由度模型进行推导搭建,并在此基础上建立了循环球式EPS转向系统PID控制系统模型。为验证控制器的效果,本文选取车速和转向盘转矩阶跃作为输入,对横摆角速度和电流进行分析,结果表明模糊 PID 控制能够很好地对目标电流进行跟踪并有效满足商用车操稳性能要求。
