智能汽车路径规划应用研究

洪 顺

（华南理工大学机械与汽车工程学院，广东 广州 510640）

前言

路径规划是智能车辆自主行驶的方向，具有影响智能车辆行驶平顺性和安全性，研究智能车辆的路径规划算法尤其重要。路径规划[1]，即为了满足一定性能通过搜索策略，规划出一条从起始点到目标终点的最优化路径。目前常用的路径规划算法有A*算法、蚁群算法、RRT算法等[2-3]，蚁群算法虽然求得的路径相对较短，但其耗时较多，不利于智能车辆的路径规划[4-5]。王海梅等人对Dijkstra算法进行优化，结合数据结构和路径搜索策略，具有启发函数性质的A*算法，两种算法的融合证明有较好的效果[6]。RRT算法[7]适用于多自由度路径规划问题，但随机分布特点会引起算法计算时间较长、路径规划非最优等不足。A*算法[8-9]发源于Dijkstra算法，具有启发性的路径搜索算法，其算法的核心在于从当前目标点搜索下一最小代价函数值，作为下一目标起点，循环往复以达到最优路径规划的目的。基于A*算法最优规划，计算效率高且较容易规划出最优路径，本文提出采用基于改进扩展搜索领域的、基于优化搜索算法的A*算法，通过Matlab/Simulink建模，搭建仿真模型，模拟室外特定区域，以验证该算法的实用性和有效性，达到智能车辆路径行驶要求。

1 传统 A＊算法

传统A*算法是一种通过启发函数来搜索路径，每次确定当前起点，重新计算代价函数，循环搜索下一目标点的路径搜索算法。启发函数常用以下公式描述：

上述公式（1）中，f（n）为路径搜索总的代价函数估计值，g（n）为实际移动代价值，h（n）为目标点到终点的估算成本，其值是估算来的。f（n）是g（n）和h（n）的和，表示智能车辆在搜索算法中总的估算成本。

传统A*算法流程图如图1所示：

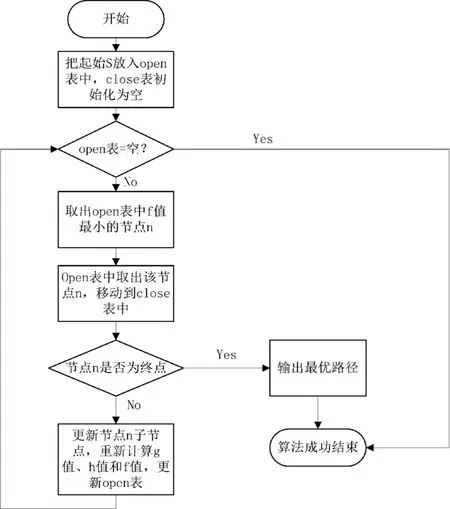
图1 传统A星算法

传统 A*算法的具体实现方式：初始化 open集和 close集，将智能车辆起点s放入open集，同时将s加入到path集，判断 open集是否为空，若为空则算法结束；否则更新open集合，重新计算open集中对应的g值、h值、f值，选出代价值f的最小值，将对应的节点n加入到path集，移除open集中的n节点，同时将n移动到close集中，表示已经成功的节点或者遍历过的节点，若节点n为终点则表示寻路成功，则输出最优路径退出算法规划；否则，更新open集重新计算g值、h值、f值，重复循环直至找到最优路径，找到最优路径时则退出算法搜索。

2 改进 A＊算法

2.1 基于扩大搜索领域的优化

传统A*算法常采用领域8节点搜索方式，这种搜索方式有一定的局限性，较难全方位为智能车辆提供可行驶区域且存在路径局部最小等不足，基于该搜索方法，提出一种改进的搜索方式，扩大可搜索领域的方法，增加智能车辆可行驶区域的可能性。

搜索领域示意图如图2所示，白色圆形表示搜索起始位置，灰色圆形代表待搜索领域，黑色圆形代表非搜索领域。传统A*算法搜索领域示意如图（a）所示，在当前搜索起始位置，通常是8领域搜索。扩展搜索领域示意如图（b）所示，将当前起始位置进行搜索领域扩展，增加领域搜索范围，向周围扩展一倍的方式进行下一可能的目标点搜索，A*算法的代价估算将有更多的选择，避免出现局部最优的情况，在细分的搜索范围中，促使搜索算法可以达到全局最优，同时对避障功能也可远离障碍物，提高规避障碍物的可能性，提供智能车辆可能的可行驶区域。

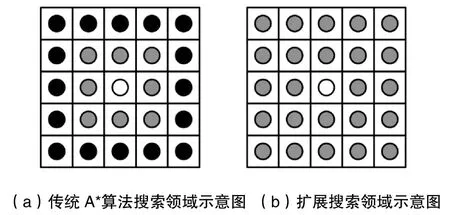
图2 优化搜索领域示意图

2.2 基于改进算法的优化

A*算法是启发性搜索算法代表算法，启发函数的选取直接影响了搜索算法的效果和实用型，该算法常用的启发函数有如下几种：

欧式距离：为两个坐标点之间的直线距离，也是路径规划中常用的距离。其公式表达式为：

上式中，（x1，y1）表示为当前坐标，（x2，y2）表示为目标点坐标。

切比雪夫距离：为两个坐标点之间最大的坐标差的绝对值，其公式可描述为：

上式中，（x1，y1）表示为当前坐标，（x2，y2）表示为目标点坐标。

曼哈顿距离：在平面或者空间，为两个坐标点之间的差值的绝对值的和，随着两个节点的动态变化，其值也会跟随变化，其计算公式可表达为：

上式中，（x1，y1）表示为当前坐标，（x2，y2）表示为目标点坐标。

A*算法是一种启发性的搜索算法，通过代价函数对每个节点进行代价评估，代价函数的选取尤其重要，本文采用距离最短的欧式距离作为代价评估，真实反应各个节点之间的相对关系，为智能车辆路径规划提供可能性的路径航点。

改进算法的优化示意图如图3所示。

图3 改进算法

改进算法具体实现方式：

（1）算法开始，需要将起始点加入到open集中，同时初始化close集、path集，将起始点并入path集，open集表示起点或者可能的行驶目标点，即可能的待检测计算的节点序号，close代表已经找的节点或者障碍物点、不可到达的节点，path集用以存放成功的目标节点。

（2）将节点n作为当前目标点，将节点n的open集更新，加入新的可搜索区域，对可能的目标节点进行遍历重新计算对应的g值、h值、f值。

（3）选出最小的f值，其所对应的节点为n，同时删除open集中的节点n，将n加入到path中。此时属于暂代目标点，需对目标点进行优化处理。

（4）判断n是否为终点，若是终点，则代表算法结束，寻求到最优的目标路径。

（5）若n不为终点则，优化判断n的子open集是否存在上一节点的open数据。

（6）若满足则重复步骤2；若不满足则重新计算暂定节点的路径f值，若最小则不用重复计算，否则重复计算路径该点的f值，若存在最小的值则优化替换，重新更新open集和path集。

（7）整个算法完成，则找到最优的智能车辆的路径。

3 仿真结果与分析

建立基于Matlab/Simulink模型，对室外特定区域实际测绘与记录，根据实际场地的构造画出室外特定区域电子地图。其电子地图如图4所示，蓝色方形代表绿化区域或者堆积区域，浅绿色区域代表停车位区域，图中蓝点代表路径航点，航点代表目标节点的位置、航向、转向信息等属性特点。图中，红色星号代表目标起始点，蓝色星号代表目标终点，规划出一条可行驶区域，即红色的线条代表规划的一次路径，当行驶的过程中遇到障碍物时，该优化算法重新规划出最新的路径，实现了避障的功能，且重新规划出的最优避障路径达到了行驶要求同时规避障碍物较远的距离，确保了行驶的安全距离，满足功能性的要求外也保证了行驶的安全性的要求。在直道线，路径相对稀疏考虑到直线部分对目标航点的要求较低，但是在弯道曲线部分，通过样条曲线拟合优化，路径航点较为密集，满足智能车辆对弯道曲线的复杂要求属性，同时弯道曲线过度平稳和曲线较为平滑。通过实验验证了，该算法的有效性能，为后续的智能车开发提供一定的技术积累。

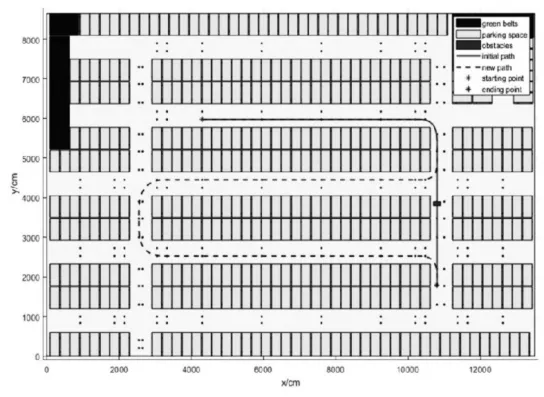
图4 仿真结果