爆破、塌陷识别研究进展综述

周少辉 蒋海昆 曲均浩 李健 郭宗斌 郑旭

1)山东省地震局，济南 250014 2)中国地震台网中心，北京 100045 3)海南省地震局，海口 570203

0 引言

近年来，随着我国数字地震台站密度逐渐增大以及观测技术系统的日臻完善，微震动事件的监测能力得到较大提升，地震台网能够捕获到更多的微震动事件信号。与此同时，随着我国经济的持续发展，因工业活动而引发的爆破、塌陷等非天然地震事件的发生频度也在逐年上升。在日常天然地震监测工作中，地震台网一方面能记录到震级较小的天然地震事件，另一方面也会记录到大量非天然地震事件(赵永等，1995)。2019年山东地震台网共记录到619次天然地震与496次非天然事件，非天然事件约占44.5%(1)山东地震监测预警中心，2020. 山东地震台网2019年地震目录. 内部资料.。

虽然非天然地震事件震级普遍较小，但其震源较浅且多发生在人员活动区域，因而具有烈度较大的特点，给当地群众生产生活带来较大影响，甚至造成严重的人员伤亡，例如2018年10月20日山东菏泽龙郓煤矿M1.5塌陷事件(在我国采矿业称为岩爆、冲击地压或矿震)即造成21人遇难；同一地区的龙堌矿井2020年2月22日发生M1.9塌陷事件又造成4人遇难。因此，相对于震级较小的天然地震事件而言，爆破、塌陷等非天然地震事件造成的人员伤亡、社会影响往往更加突出。就地震监测体系而言，如何对实时记录事件进行快速准确的识别分类，不仅对政府部门应急管理有重要作用，对于及时消除群众恐慌以及企业生产经营活动也具有重要意义。快速有效地区分天然地震与非天然地震事件已成为目前地震监测工作中面临的重要问题之一。

在波形信号记录中，爆破、塌陷等非天然地震事件与天然地震有一定的共性，特别是近年来各类组合爆破与包含多次小塌陷的矿区塌陷事件的出现，使得地震仪记录到的波形异常复杂，地震监测值班员仅仅通过日常积累的基于波形在信号方面的直观特征很难判定具体事件类型，且不同人员的事件类型判定结果多有差异，对及时有效地甄别爆破、塌陷等非天然地震事件造成一定困难。据此，本文尽可能全面地总结国内外关于天然地震与爆破、塌陷事件的研究进展，梳理二者的联系与区别，着重归纳、介绍目前国内外关于天然地震与爆破、塌陷事件识别判定的主要手段和方法。

1 爆破与塌陷

日常地震观测记录到的所有由于非天然因素引发的与天然地震波形特征类似的事件，均称为非天然地震事件(林伟等，2004)。换言之，非天然地震事件主要指由人工干预或人类活动间接引发的地震事件，其涵盖范围宽泛，主要包括爆破、塌陷、核爆、水库蓄水诱发地震等。其中，90%以上的非天然地震属于爆破事件(林伟等，2004)。由于塌陷事件往往发生在矿产资源开采区、喀斯特(即岩溶)地貌发育区、黄土高原居民区等，塌陷事件所造成的社会生产生活及人员伤亡情况往往异常严重。2004—2014年，我国发生的35次矿区塌陷事件共造成300余人死亡，上千人受伤(姜耀东等，2015)。因此，从非天然地震的数量及造成人员伤亡的社会影响情况出发，本文将重点论述爆破与塌陷地震。

1.1 爆破

爆破是爆炸产生的工程效应，是极高速进行并自动传播的化学反应瞬间实现势能转化为机械能的过程(包淑娴，2011)；爆破地震是指炸药在爆炸瞬间能量极速释放，其中的一部分能量转化为地震波向外传播并引起地下振动及造成一定破坏效应的一种非天然地震事件。在目前的社会生产生活中，爆破广泛应用于采矿与各类岩土工程施工中。

1.2 塌陷

塌陷是指在外力作用下地表岩体或土体向下陷落的一种地质现象；塌陷地震是指由于岩层崩塌陷落而形成的非天然地震事件。也有研究定义塌陷地震是因地下岩洞塌陷、大型山崩或矿井顶部塌陷而引起的地震事件(杨慧等，2018)。

由于发育的地质条件和作用因素不同，塌陷一般分为岩溶与非岩溶塌陷两类。岩溶塌陷指在外力作用下覆盖于可溶性岩层之上的松散土石体向岩层中发育的溶蚀洞穴运移而导致的地面变形破坏。发生于非岩溶地区的塌陷统称为非岩溶塌陷，包括矿区的采空塌陷、黄土高原地区的黄土塌陷等。

岩溶塌陷通常规模较小，缓慢产生，由于其并不是瞬时发生，往往不会对人类社会生活造成破坏性影响。而非岩溶塌陷往往瞬时发生且多发生在人员活动区域，如采空塌陷通常发生于矿区，黄土塌陷区则有大量居民居住于黄土窑洞等。陕西榆林地区近年来多次发生3.0级左右的黄土塌陷事件(汤静雅等，2019)，2018年山东各地发生的ML2.5以上塌陷事件达16次①，个别塌陷事件造成了一定人员伤亡，产生较大的社会影响。因此，非岩溶塌陷一旦发生便可能成为一种灾害。其中，发生于采矿活动区域的采空塌陷，主要指矿井高应力区内煤体、岩体及断层在受外界扰动时瞬间失稳破坏，同时释放出巨大能量，进而在矿区周围引发剧烈振动及巨大破坏的矿山动力现象(邴绍丹等，2007；钱七虎，2014)，也称为矿震，包括矿产开采中发生的岩体冲击地压、隧道工程中发生的岩爆等。矿震的成因主要是在地面、浅层(几百米)和深层(千米以下)的矿山开采过程中，人为改变了原本稳定的地质结构，导致矿区受力不均(姜耀东等，2015)。全球研究结果表明，开采深度大于500m的矿山就有发生3级以上塌陷地震的可能(唐子波，2011)。就我国大陆地区而言，采空塌陷分布较广泛，尤其是黑龙江、山西、山东等矿产资源丰富的省份更为严重(张玉中，2005)。震源浅、震级低、烈度高是非岩溶采空塌陷地震的主要特征(贺秀全等，1997)，如山西地区虽然未发生过超过ML4.0的塌陷地震，但震中最高烈度却达到Ⅸ度，且井下破坏烈度往往高于地表，其在一定范围内随震级和深度的增加而增大(靳玉贞等，2015)。

2 爆破和塌陷事件波形记录特征

爆破、塌陷与天然地震均为瞬间发生的失稳事件，部分能量以弹性波的形式从震源辐射出来，并以地震波的传播方式被地震仪所记录。各类振动事件发生后，其在地震台网记录的地震波形图上均有一定的共性。地震台网记录的天然地震与非天然地震反映在地震波形图上的共性主要有(苏莉华等，2011)：①记录波形一般表现为纵波、横波、面波三大部分，并依次出现；②面波的周期最长，S波次之，P波最小；③纵波振幅小于横波振幅，面波振幅最大；④记录波形的持续时间、波形最大振幅均随事件震级的增大而增大。

同时，由于地震波形特征与震源机制、传播路径等一系列因素有关，不同类型事件的地震波又有其独有的波形特征。

2.1 爆破事件波形记录特征

从波形记录特征来看，数字记录的爆破震相特征不如模拟记录明显(赵永等，1995；张萍等，2005)，震中距由小到大的台站记录的非天然地震波形相似性较差(林伟等，2004)。爆破事件的波形特征主要有：

(1)垂直向P波初动向上(图1)。爆破是由化学爆炸引起体积的突然膨胀，属于膨胀源，因此其直接产生的压缩波并无象限分布，即无论记录到爆破事件的台站所处地理位置如何，其垂直向的P波初动方向均向上。

(2)P波初动振幅较大，存在较强的P波群。由于爆破在瞬间发生，其震源很浅，在进行爆破时，炸药体积较小且堆积较为规则，更接近于“点源”，理论上可认为爆破过程是在一理想的球形腔内形成汽化区、液化区、塑性区。在爆破过程中，岩石直接受到的力为正压力而非剪切力，因此理论上爆破只会直接产生压缩波而无剪切波。台站记录所接收到的剪切波是由于破裂不沿初始力的方向破裂而发生切变产生的，产生这种现象的主要原因是爆破方式差异、波的传播路径不均匀性等(Yldrm et al，2011)。因此，人工爆破一般有较强的P波群，而S波则相对较弱，距离爆破点越近S波越不清晰；由于其瞬间发生，体波为瞬时脉冲型，在波形中具体表现为爆破的波形初动强而尖锐，且在垂直方向上P波振幅与S波振幅相当或者大于S波振幅，即俗称的“大P头”(赵永等，1995；Allmann et al，2008)。

(3)爆破持续时间短、衰减快。由于人工爆破瞬间发生，震源浅，波的传播路径很大一部分是松散的地表浅层(土层)，其介质密度较低，因此爆破产生的波在传播过程中能量损失较大；随着传播距离的增大，其能量衰减非常快；整个波列的持续时间也较短，一般为几秒(李发等，2012)，尤其是横波，爆破事件的横波明显比天然地震衰减快。林伟等(2004)用波的持续时间τ来度量振幅衰减快慢，τ值越大则振幅衰减越慢，其对广东省内28个爆破事件和26个天然地震τ值的对比研究结果显示：①震中距和震级相同时，同一台站记录的天然地震事件τ值大于爆破事件；②对不同震中距台站记录的同一事件，天然地震τ值变化幅度不大，而爆破事件τ值变化幅度较大。Kiszely(2001)对匈牙利爆破与天然地震的尾波持续时间研究结果也显示，天然地震的尾波持续时间明显大于爆破事件。

(4)爆破事件各震相急促、短暂、清晰明了(图1)。与天然地震震源深度较深、地震波在传播过程中经过多层介质反射与折射不同，爆破震源很浅，波的传播路径单一，通常在强度较低的松散介质中传播，因此爆破震相较为简单，且波的高频成分极易被吸收(Kiszely，2001；王婷婷等，2013)，故经过一定距离的传播后，爆破波形会显得很“干净”，表现出波列光滑、涟波较少的特征。同时，爆破事件的波形频谱图上也表现出类似的特征，张春贺等(2006)利用周期-频度谱分析发现，天然地震的不规则指数大于爆破事件。

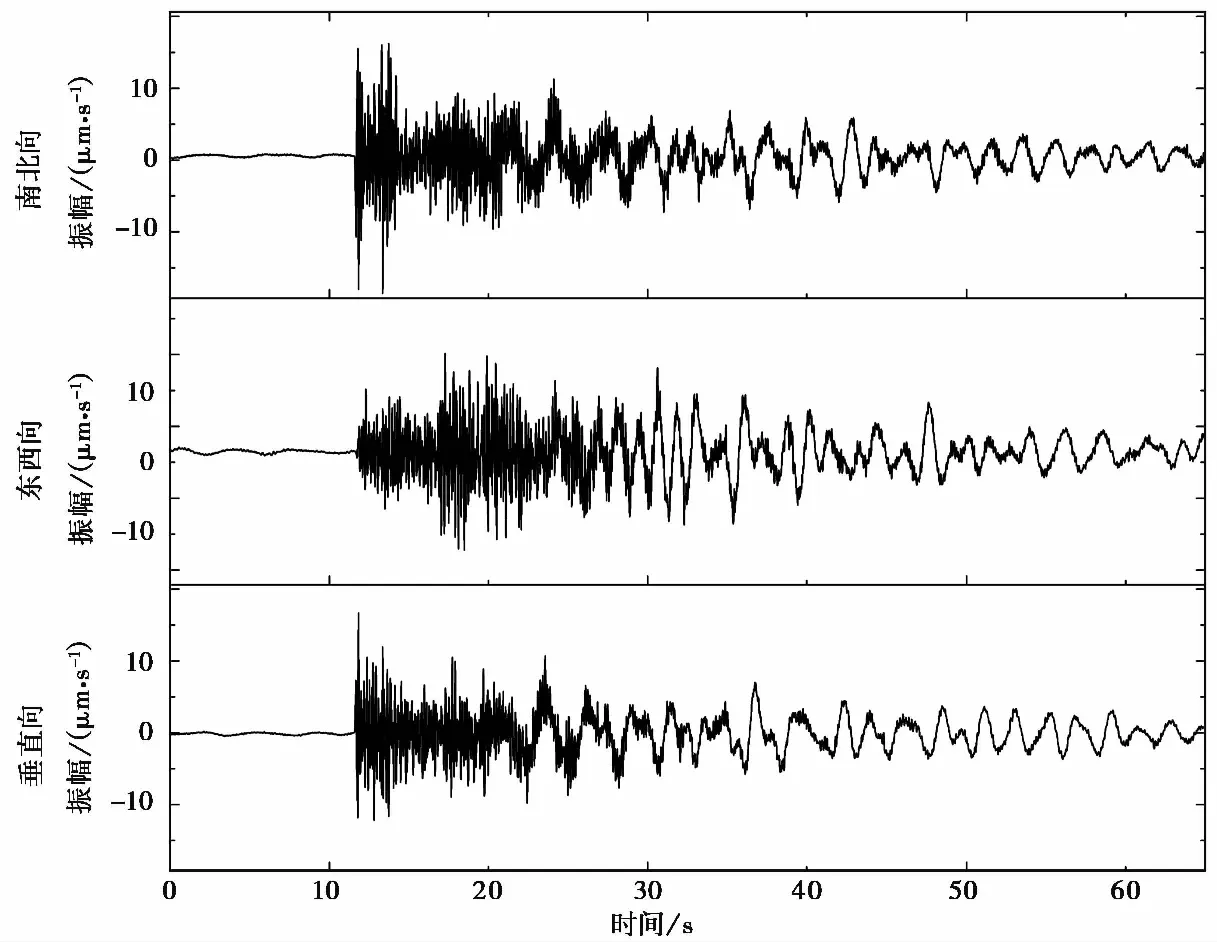
图 1 GUY台记录震中距约50km的2019年3月21日江苏响水ML3.6爆破事件波形

(5)出现短周期瑞利面波且发育较好(图1)。由于爆破过程会在爆炸区产生多个层面，特别是在溶化区两侧会形成2个自由界面，在与其相邻的2个区的作用下，会在自由界面激发沿地表传播的瑞利波。研究显示，在震中距大于5km后，数字化宽频带地震计便有可能记录到瑞利型短周期面波，瑞利波波列形态与其他面波表现形态基本一致，一般波群仅1～2组，振幅一般呈现逐渐增大、随后又逐渐减小的特征(赵永等，1995)。但由于爆破震源通常较浅(有些几乎为零)，可近似于在均匀的介质中传播，因而瑞利波频散特性并不明显(汪贵章等，2010)。也有研究显示，震中距在50km左右的爆破震相中有较清晰的周期较大的面波，随着震中距的增大，面波更为清晰(刘莎等，2012)。与此形成对照的是，在震中距200km以内，天然地震面波一般不发育。

(6)具有较规律的时间和空间特性。与发震时刻随机性较强的天然地震不同，爆破的发生时间可人为控制，具有一定的规律，如深夜、整点、下班时间等。同时，对于短期内连续发生的爆破，其每次爆破之间的时间间隔相等或接近，且间隔时间较短(Ursino et al，2001；霍祝青等，2015)。在空间上，大多数爆破除震源较浅这一显著特征外，生产活动所导致的爆破地点范围较为集中，往往在固定的几个地区重复进行。

(7)爆破的P波与S波最大振幅比远大于天然地震(图1)。振幅比表征了地震的动力学特性，其并不取决于地震波振幅的绝对值，基本上与震级无关，即振幅的比值受震级、地震仪放大倍数及频率特性的影响较小。由于爆破直接产生的波只有压缩波，而剪切波是派生波，因而人工爆破近源区的地面垂直向振动加速度、振动速度等均比水平运动大，其S波最大振幅小于P波，即AP/AS>1(Yldrm et al，2011)。王婷婷等(2013)对北京及邻近区域29个爆破与33个地震事件的P波与S波最大振幅比的研究结果也显示，爆破事件的AP/AS远大于天然地震。与此相关联的是，爆破的mb/MS，即体波震级mb与面波震级MS之比，也大于天然地震(边银菊，2005)。

(8)存在大周期现象(图1)。周期是地震波的动力学特性之一，依赖于震源机制、介质结构和介质性质等诸多因素。对于单台记录的整个地震波列而言，爆破的周期变化不大，S波往往出现类似正弦型的稳定周期振动现象，在S波之后一般存在周期较大的脉冲振动(汪贵章等，2010)，而天然地震则一般具有清楚的脉动和高频特点，优势周期从初至开始通常随时间逐步增加，一般Sg波周期大于Pg波。同时，由于爆破的高频成分随震中距增加极易被疏松的介质吸收，因此爆破事件的P波周期明显“变”大(赵永等，1995)。有研究认为，当震中距小于5km时，爆破与天然地震的P波和S波速度型周期近似相等，约为0.02s～5Hz，当震中距离大于5km后，爆破的P波和S波速度型周期明显大于天然地震的体波周期(汪贵章等，2010；李发等，2012)。

(9)爆破事件波形记录的频谱特征与天然地震明显不同。在频域方面，人工爆破震源浅，经过松散地层，波的高频成分被吸收较多，即地层对爆破产生的波的衰减起到一种低通滤波作用。因而爆破的频带范围较窄，频谱较天然地震更为简单，能量较为集中，且其高频成分的能量衰减快于低频，即波列中有明显的低频成分(Kiszely，2001；唐兰兰等，2009)。与天然地震具有清楚的脉动和高频特点不同，爆破频率比天然地震频率低，尤其是Sg波之后频率明显较低、周期变大(刘莎等；2012)。

2.2 塌陷事件波形记录特征

无论其成因还是波形特征，塌陷事件均比较复杂，不同类型、不同深度发生的塌陷事件均有差异。如金属矿山中的矿山地震特别接近天然地震，井下塌陷由于井水的渗透和气体的透入，在地震波形图上往往会体现出断层的蠕动性质(赵永等，1995)。由于井下冲击地压事故造成的塌陷地震，往往其波形初始有部分类似于爆破波形特征，后续部分则类似于普通塌陷波形。归纳起来，绝大多数塌陷地震所激发的波形具有以下主要特征：

(1)P波初动向下(图2)。由于塌陷为岩层下方出现空区、向下陷落，因而大面积来压后向下冒落的瞬间，其向周围介质施加的力为拉力，即内向爆破产生压缩波。因此，理论上无论周围的台站所处地理位置如何，所记录到的垂直向P波初动方向均应向下。就其机制而言，可能有双力偶机制、偶极矩机制和非力偶机制的“内向爆破型”，其破裂体并非剪切滑动，而是“会聚”型的失稳(赵永等，1995)。

图 2 ZCH台记录的2020年7月12日山东邹城ML2.3塌陷事件波形

(2)整个波段波形简单、规则，高频成分较少(图2)。由于塌陷震源较浅，地震波主要在密度小的介质中传播，因此高频成分同样易被路径介质吸收。同时，P波、S波成组出现，形成波列。由于塌陷不是一次完成，常常反复几次，甚至可能伴有岩体或矿体的滚动等情景，在地震图上可形成几组P波和S波，波列初看有些像远震的体波段(汪贵章等，2010)。

(3)Sg波后大周期瑞利面波发育(图2)。由于塌陷往往不是瞬间一次完成，存在多次塌陷且震源浅，因而同样会在自由界面激发沿地表传播的瑞利波。塌陷面波的周期比天然地震大，面波速度型周期一般在0.1s～0.2Hz之间，具有明显的正频散特征，即大周期在前、小周期在后(李发等，2012)。

(4)持续时间较短、衰减快(图2)。塌陷记录持续时间通常1～2min，超过5min的较少，塌陷事件水平分向与垂直分向持续时间的比值小于天然地震(赵永等，1995)。

(5)周期较大(图2)。整体而言，最初到达的P波周期一般较小，由于塌陷震源较浅，纵波和横波到达时间紧凑，并且由于地震波主要在稀疏介质中传播，高频成分被介质吸收，因而横波到达后周期明显增大。汪贵章等(2010)研究显示，塌陷事件体波波段的速度型周期一般在0.02s～16Hz，而天然地震的周期一般在0.1～0.3s。

(6)垂直向P波初动振幅多数大于水平向。由于塌陷事件激发的波射线经过的路径上存在很强的速度梯度，波速在浅部小于深部，因而会造成体波传播路径向上弯曲(唐子波，2011)。就其振幅变化而言，开始变化较小，横波到达后振幅明显增大(王风等，2013)。

(7)与构造地震相比，塌陷地震主要发生于顶板坚硬的采空区(只有顶板坚硬，才会形成大面积的采空悬空区域)(贺秀全等，1997)，因而塌陷地震震中局限于矿区、大的工程建设区域、岩溶地区等特定区域，震中地点较为固定，分布范围较小，无明显的迁移现象(刘莎等，2012)，一般活动范围在几十万平方米以下。同一塌陷地震，其主震、余震的位置变化极小，纵波和横波走时差基本不变。同时，塌陷事件震源深度分布存在较为普遍的临界深度现象，最浅约为200m(北京门头沟煤矿)，最深的不超过7000m(李铁等，2007)。

(8)塌陷事件的振动频谱较为单一，且频率域一般低于天然地震和爆破事件，约为1Hz，其P波、S波的卓越周期近似相等，为1～1.2s(赵永等，1995)。也有报到显示塌陷地震Pg和Sg记录波形的频率无明显变化(苏莉华等，2011)，塌陷地震的拐角频率、应力降(图3)、峰值频率小于天然地震(刘莎等，2012)。

图 3 天然地震与塌陷事件的应力降统计

3 爆破、塌陷等非天然事件的识别方法

自20世纪下半叶以来，国内外许多研究者致力于地震与爆破、塌陷等非天然事件的识别方法研究(Dowla et al，1990；Kchui，1992；边银菊等，2002；边银菊，2005；张萍等，2005；Kuyuk et al，2011；赵刚等，2017)。一个好的识别方法应具有以下特点(Douglas，2007)：①可以区分各类事件类型；②可以在理论上加以证明，即有明确的物理意义；③使用简捷。前期的工作大多基于记录波形以及波形特征对比，力图寻找具有一定物理意义的事件类型识别判据(郑秀芬等，2006)。

3.1 直接基于波形时频特征的事件类型判定

3.1.1 波形时频分析对比法

理论上，不同震源模式辐射的理论地震波谱不同。有研究者根据对台站记录的爆破、塌陷和天然地震波形的时频分析对比，来实现对天然地震与爆破、塌陷等非天然事件的识别(张萍等，2005；郑秀芬等，2006；刘莎等，2012)。该方法主要从经验统计的角度出发，通过对各类事件的波形特征及差异进行总结，并结合对时域信号进行快速傅立叶变化后的频域信号特征对比分析，对事件类型进行定性识别分析。张萍等(2005)利用由布龙圆盘位错模式给出地震事件的高低频谱值、拐角频率、零频谱值等震源参数来识别地震事件类型，认为这些频谱差异特征可作为地震与矿震、地震与爆破判别的有意义的指标。也有研究者利用基于波形互相关技术的模板匹配法来识别事件类型，如Kahbasi等(2016)对德黑兰矿区爆破的研究显示，与选取的爆破波形模板互相关系数大于0.6即可判定事件类型为爆破，其对该地区2006—2013年的爆破事件识别准确率高达96%。此外，也有研究者利用倒谱分析(魏富胜等，2003)、周期-频度谱分析计算天然事件与非天然事件的不规则指数(张春贺等，2006)、波形复杂度(马举，2014)、P波与S波时间域上能量差(魏富胜等，2019)等参数识别事件类型。

3.1.2 小波变换

小波变换将地震波信号按二分法在频率域中依次进行分解，可将振动信号分解到不同频带上，进而显示信号在不同频带的能量分布规律(Kchui，1992；凌同华等，2004)。与天然地震具有清楚的脉动和高频特点不同，爆破、塌陷事件的频率域比天然地震低，频谱相对简单、能量较为集中、波列中有明显的低频成分(唐兰兰等，2009)。因此，可利用小波变换类的方法来区分天然地震与爆破、塌陷等非天然地震事件。刘希强等(2003)运用小波变换“能量”线性度方法来判定事件类型，结果显示天然地震的“能量”线性度主要集中在-2～1之间，爆破或塌陷集中在2～3.4之间；Beccar-Varela等(2016)通过小波变换获得美国亚利桑那州10km空间范围内3.0～3.5级地震和爆破事件的时频能量特征，结果显示，与天然地震相比，爆破能量较为集中，信号能量持续时间短。也有研究者尝试使用小波包分解来识别天然地震与爆破、塌陷等非天然地震事件，与仅对信号低频部分进行变换的小波变换不同，小波包变换也对高频部分实施变换，同时，能根据信号特性和分析要求自适应地选择相应频带与信号频谱相匹配，是一类比小波变换更精细的变换方法(Mallat，1989；Daubechies，1990；韩绍卿等，2010)。曾宪伟等(2010)基于5层小波包变换获得信号的P(或S)波段时频谱值及其达到最大时对应的频率，并以此为定量识别指标，识别银川台记录的19次爆破与14次地震，结果显示，虽然针对单个台站确定的阈值对事件的识别准确率在80%以上，但不同台站记录的同一区域内的地震和爆破的识别阈值均存在差异。毛世榕等(2018)基于4层小波包变换对广西地区17次塌陷事件和22次浅源地震事件的识别研究显示，天然地震的优势频段为0～20Hz，塌陷优势频段为0～10Hz，其基于波形4层小波包变化得到的16维数据特征的识别准确率可达89.5%。

以上识别方法主要是从一定事件波形的时间域或频率域特征出发，对各类事件的各自特征作一定的定性分析判定，虽也有部分方法尝试提出定量的识别判据，但也多为单项识别指标。从目前实际情况来看，结合研究者个人直观经验的地震波谱对比分析，可在一定程度上满足地震监测台网值班员日常工作中事件类型的判定需求。但由于上述方法只是简单地利用波形记录的直观特征进行识别，属于定性分析，而探寻可直接运用于计算机自动识别的高效识别判据必定是基于事件类型特征的定量判定，且由于波形记录是震源类型、传播路径、记录仪器设备等一系列影响的综合反映，最终事件类型的判定实际上是一个多特征的综合分类问题(王婷婷，2013；Taylor，2011；Kahbasi et al，2016；陈润航等，2018；范晓易等，2019)。

3.2 基于模式识别算法的事件类型判定

与上述仅根据地震与爆破、塌陷的波形特征来人工识别事件类型的做法不同，20世纪末以来有研究者将统计学中的模式识别算法引入地震学，以此来实现地震与爆破、塌陷事件类型的自动识别，取得了一系列重要进展(Dowla et al，1990；边银菊等，2002；边银菊，2005；Kuyuk et al，2011；王军，2018；范晓易等，2019)。模式识别是指对表征事物或现象的各种形式的信息进行处理和分析，并以此对事物或现象进行描述、辨认、分类和解释的过程(张博，2013)。目前，地震学中天然与非天然地震的模式识别方法主要有最小距离法、改进的连续亨明方法、Fisher方法、逐步代价最小决策法(SAMC)、支持向量机和神经网络等。

3.2.1 最小距离法

最小距离法是一种极其简单的模式分类器，其决策函数的核心思想是确定判定样本与决策重心之间的距离，进而判定其所属类别。决策函数的数学实质是基于对模式的采样，估计出各类模式统计样品参数的特征均值与所需判定样品之间的欧氏距离，以此来判定样品的类别，被判定样品的相应参数距哪一类别均值的距离近，则属于哪一类。张博(2013)利用最小距离法，并基于P波初动、P波最大振幅与S波最大振幅比、P波初动振幅与S波最大振幅比、P波瞬时频率复杂度与P波谱比等5个特征，对河北怀来及周边地区26个爆破与18个天然地震进行综合识别，研究结果显示识别正确率为82%。王婷婷等(2013)采用最小距离法对北京及邻近地区33个天然地震和29个爆破波形数据的识别研究表明，如仅利用最小距离法分别通过单个特征判据进行识别，识别结果正确率为60%～92%，如挑选出单判据识别率较高的P波初动、P波最大振幅与S波最大振幅比、P波初动振幅与S波最大振幅比3个特征判据，并利用最小距离法对其进行综合识别，则识别结果正确率为94%。此结果表明挑选合适的特征判据并用最小距离法进行综合识别，可较好地实现地震事件类型识别。最小距离法的计算方法简单明了，是一种简单快捷的分类判别方法，但需要注意的是，使用最小距离法进行模式分类识别，其决策重心(参数均值)必须能够真实反映其固有特征，即对于团状分布的各类样品有效(张海侠等，2010)。同时，要求“类间距离最大、类内距离最小”，即不同类别间决策重心(参数均值)的距离要显著大于同一类别内部参数与各自决策重心(参数均值)的距离，否则最小距离分类器的分类效能较差。

3.2.2 改进的连续亨明方法

王碧泉等(1988)根据连续亨明算法提出一种寻求样本与亨明核间距离的改进连续亨明方法(简称ICHAM)，以此来识别震源事件类型。其核心思想和主要步骤为：①确定需识别类别的每一类样本特征均值与类内离散度；②根据不同类别样品各自类内离散度确定判定函数的亨明核；③设定连续亨明方法的分类规则，判定事件类型。王婷婷等(2013)采用改进的连续亨明方法对北京及邻近地区33个天然地震和29个爆破波形数据的识别研究表明，基于单个特征判据识别天然地震和爆破的准确率为60%～92%；进一步挑选出单判据识别率较高的P波初动方向、P波初动振幅与S波最大振幅比、P波最大振幅与S波最大振幅比3个判据，利用改进的亨明算法对其进行综合识别的准确率为95%。此结果同样表明，利用改进的连续亨明方法进行综合识别，仍需挑选合适的特征判据。

相对单纯求特征均值的最小距离算法而言，改进的连续亨明方法由于加入类内离散度这一控制因素，适用于更为一般的样品分布，即每类样品可以是团状分布，也可以不是团状分布(边银菊，2005；王婷婷等，2013)。需要指出的是，该方法对过多特征同时识别时，会产生多维空间的“维数灾难”问题，因而一般只适用于低维空间问题(Andrew，2002)。

3.2.3 Fisher方法

针对多维空间的“维数灾难”问题，Fisher方法通过压缩特征空间维数，进而通过多维特征同时对事件性质进行识别(赵静，2008)。该方法的基本思想是投影，首先通过一个投影矩阵，将高维数据点投影到某一方向上，在该方向上类间距离最大、类内距离最小，即找寻出最优映射方向，随后设定Fisher方法中样品事件与最优映射方向的分类阈值，进而判定事件类型。其主要计算步骤包括(Andrew，2002；何树生等，2017)：①计算样本均值与类内离散度矩阵(与亨明方法第一步类似)；②求取最优投影方向，设在d维特征空间的w方向上，同类样本可以尽可能集聚而异类样本可以尽可能分开，则d维特征样本在该w方向上进行投影，便降为一维特征样本；③设定样品事件与最优映射方向的分类阈值，判定事件类型。边银菊(2005)利用Fisher方法对全球248次地震与288次爆破的识别研究表明，采用mb/MS单个特征判据的识别结果准确率可达95%，具有较高的识别正确率；但赵静(2008)利用Fisher方法对首都圈测震台网107个台站记录的35个天然地震事件和27个人工爆破事件的识别研究表明，通过谱比值、波形复杂度、自相关系数等特征判据，最终识别正确率却仅为60%左右，故认为Fisher方法的线性判别函数只能对判别区域为单连通的线性可分模式类进行正确分类，对于判别区域分界面比较复杂的线性不可分模式类，则分类效果较差。

3.2.4 逐步代价最小决策法

受统计模式识别中模板匹配类的动态时间规整(DTW)算法的启发，张博(2013)提出基于逐步代价最小决策法(SAMC)，以此来识别爆破与地震。该算法的核心思想为：首先定义代价函数，实现路径最优化，进而求得全程代价函数来区分地震和爆破。其主要步骤包括：①识别地震与爆破的特征提取，分析每一项特征，找到最优分类阈值；②确定参考模板和测试模板；③建立分类器，将测试模板的特征向量序列通过某个路径投影到参考模板序列上，每一步投影均对应一个代价函数d，最终累计所有的代价函数得到全程代价函数D，最小的D即为最优全程代价函数，进而确定分类准则；④进行检验，用测试模板的全程代价函数值，根据相应事件的性质(地震或爆破)按分类准则进行判别，计算检验样本集的识别率。张博等(2014)利用逐步代价最小决策法，对北京及其周边地区33次地震和29次爆破中提取的初动方向、P波最大振幅与S波最大振幅比、P波初至振幅与S波最大振幅比、P波最大振幅与尾波持续时间比、S波最大振幅与尾波持续时间比等5个分类特征量进行识别，识别率为90%；从5个特征量中选择较好的初动方向、P波最大振幅与S波最大振幅比、P波初至振幅与S波最大振幅比3个特征量进行识别，识别率为92%；其还另外选择研究区的13次事件(检验样本)，对分类函数进行u检验，5个分类特征量的识别率为92%，3个分类特征量测试模板的识别率达到100%。

该算法可在确立最优函数时，对事件各类特征分别赋予不同权重，进而将各类特征在识别事件时的效果优劣尽可能地考虑到。同时，代价函数值的绝对值可以作为评判该事件识别结果的可信度。然而，想要找到最优代价函数，则必须找出所有的全程代价函数，而这往往需要非常大的计算量。

3.2.5 支持向量机

Vapnik等(1963)基于统计学习理论，提出了一种新的向量分类识别算法——支持向量机(SVM)。其主要思想为：以结构风险最小化为原则，根据有限的样本信息，在特征空间中建构最优分割超平面(分类器)，来实现对事件的分类识别。此外，对于在输入空间中不能直接线性分割的数据集，引入核函数，通过使用非线性映射算法，将低维输入空间中的线性不可分样本映射到高维特征空间，达到线性可分或近似线性可分，进而在特征空间建立一个最优分离超平面，相当于在输入空间产生一个最优非线性决策边界(Cristianini et al，2004；王军，2018；蒋一然等，2019)。

从实际算例来看，王军(2018)采用支持向量机的算法对上海测震台网记录的2008年11月至2016年9月34个浙江舟山爆破事件和66个天然地震事件进行回溯性识别检验，准确率约为89%；范晓易等(2019)首先对天然地震、爆破及塌陷的波形数据进行小波变换，再利用小波转换系数提取香农熵特征，最后基于支持向量分类机LIBSVM多类模式识别方法对香农熵特征进行分类识别，其判定结果准确率在80%～95%之间。

支持向量机的算法具有较强的非线性处理能力，通过调整核函数，不断将原始数据映射到高维空间，实现事件类别可分(Cristianini et al，2004)。同时，该算法还具有自主更新学习功能，可不断增加新的事件到学习样本库，进而不断更新修正预测识别方案，提高预测识别效能。但需要指出的是，在实际应用中，核函数及其参数选择是关键，核函数及其参数选择的好坏直接影响分类器性能的优劣，因此针对不同事件的不同样本，采用不同的训练方法探寻出的分类识别器会有较大差异，且计算复杂、学习过程繁琐，找寻事件识别普适性分类器难度较大(Cristianini et al，2004)。

3.2.6 神经网络

人工神经网络模型种类繁多，目前已发展了上百种神经网络。常见的神经网络包括：感知器神经网络、BP(Back Propagation)神经网络、自适应线性神经网络、自组织竞争神经网络、学习矢量量化(LVQ)神经网络等。据统计，在人工神经网络的实际应用中，BP神经网络是目前应用最广泛的神经网络模型之一，约80%～90%的人工神经网络采用BP神经网络或其变化形式(贾宝新，2019)。

BP神经网络是一种按误差逆传播算法训练的多层前馈网络，为前向网络的核心部分，是一种有监督的误差纠正学习算法。其基本思想为：基于最小平方误差准则和梯度最速下降算法来确定权值调整准则，使用梯度搜索技术，使网络的实际输出与期望输出均方差最小。BP神经网络模型拓扑结构包括输入层、隐含层和输出层。Dowla等(1990)利用BP神经网络对美国西部83次地震和内华达87次核爆事件的识别研究显示，其单台的识别率可达93%以上，而采用4个台综合的台网识别率为97%，该识别率比采用Fisher方法对相同事件的识别率高很多。刘方斌等(2020)利用BP神经网络对随机选取的山东地区30个天然地震、20个爆破、20个塌陷进行训练，并分别选取10个天然地震、爆破与塌陷事件进行测试，结果显示，30个测试样本中只有1个事件类型识别错误，但总的来看，其训练及检验样本数量偏少，结果尚需进一步验证。

BP神经网络能学习和存贮大量的输入-输出模式映射关系，而无需提前揭示描述这种映射关系的数学方程，即其可逼近任意连续函数，具有较强的非线性映射能力。同时，其解决了求解非线性连续函数的多层前馈神经网络权重调整问题，学习规则简单，便于计算机实现，具有很强的记忆能力及自学习能力(李冬梅，2012；贾宝新，2019)，对各类事件的识别能力高于上述几类算法。然而，由于BP神经网络采用梯度下降法探寻最优方程，对于非线性方程势必会存在收敛速度慢、局部极值等缺点。

此外，用来识别天然地震与爆破、塌陷事件的方法还有矩阵决策算法(边银菊等，2012)、集成学习的BP-Adaboost方法(赵刚等，2017)、最近邻支撑向量特征线融合算法(李夕海等，2009)、基于无监督的自组织特征神经网络算法(Kuyuk et al，2011)、区域P/S二维网格数据的统计识别(Taylor，2011)等。近年来，也有部分学者尝试利用人工智能领域的卷积神经网络、深度神经网络等来识别地震与爆破事件(陈润航等，2018；隗永刚等，2019)。

4 讨论与总结

(1)非天然地震是由人工干预或人类活动间接引发的地震，90%以上的非天然地震为爆破地震，而发生于矿区的塌陷是各类非天然地震中造成人员伤亡最多的非天然地震事件。爆破主要缘于爆炸产生的工程效应；塌陷地震是由岩层崩塌陷落而形成的地震，塌陷可分为岩溶塌陷与非岩溶塌陷两类，其中发生于采矿活动区域的采空塌陷也称矿震。

(2)爆破、塌陷与天然地震发生后，部分能量以弹性波的形式从震源辐射出，并以地震波的传播方式被地震仪所记录，虽然在地震台网记录的各类事件的波形存在一定共性，但由于震源类型、波的传播路径、震源深度等不同，其波形记录在P波初动、初动振幅、P波与S波最大振幅比、持续时间、震相、短周期面波发育情况、发震时刻、空间位置分布以及频谱特征等方面均存在一定的差异，因此结合经验可简单根据各类波形特征来识别各类事件类型。

(3)目前关于地震与爆破、塌陷等非天然事件的定量识别方法主要有两类，一类为直接基于波形在信号、数据方面的特征，通过定性分析来进行事件类型的判定，如波形时频分析对比法、小波变换、相关系数等；另一类是统计学领域诸如模式识别等算法，其利用统计算法综合考虑多个事件特征判据的定量判定阀值来实现地震与爆破、塌陷事件类型的识别。

直接基于波形在信号、数据方面特征的定性分析进行事件类型判定，在日常实际工作中结合长期的经验积累，在一定程度上可以简单高效地识别爆破、塌陷和天然地震。然而，若想探寻出可直接运用于计算机自动识别的高效识别判据必定是基于事件类型特征的定量判定(建立各类判据的有效阈值)，且由于波形记录是震源类型、传播路径、记录仪器设备等一系列影响的综合反映，最终事件类型的判定应该是一个多特征的综合分类问题。因此，利用该类方法实现事件类型判定的计算机自动化难度较大。

利用统计算法来实现地震与爆破、塌陷事件类型自动识别的方法主要有最小距离法、改进的连续亨明方法、Fisher方法、逐步代价最小决策法、支持向量机、前馈神经网络等。最小距离法与改进的连续亨明方法为早期简单的统计分类算法；Fisher方法解决了多维特征造成的“维数灾难”问题，是一种较好的特征提取方法；逐步代价最小决策法可在确立最优函数时，对事件各类特征分别赋予不同权重，进而考虑到各类特征在识别事件时的效果优劣，但其需找出所有的全程代价函数，计算量较大；支持向量机具有较强的非线性处理能力，且具有自主更新学习功能，是神经网络出现前公认的最好算法，然而核函数及其参数选择的好坏直接影响分类器性能的优劣，因此找寻事件识别的普适性分类器难度较大；BP神经网络学习规则简单，便于计算机实现，具有较强的自学习能力，其对各类事件的识别能力相比上述几类算法要高很多，然而，由于BP神经网络采用梯度下降法探寻最优方程，存在收敛速度慢、局部极值等缺点。

上述各类识别方法本质上均需首先提取有效特征判据，随后直接利用判据或利用几类算法建立分类器，最后实现对事件类型的判定。各类识别算法虽取得良好效果，但人为从事件记录中提取某些特征，即对数据进行了降维使用，并未将事件记录的全部信息用于事件判定，这不但增加了处理过程的复杂性，且损失了大量的原始事件信息，因而成为到目前为止并未找出一种简单实用的事件类型识别方法的根本原因。因此，有必要使用一种可从全部事件记录中自动提取各类信息并可组合底层特征的算法来对各类事件进行判断识别，随着人工智能的飞速发展，将语音识别、人脸识别等人工智能领域的相关技术方法引入地震学事件类型判定中，或许会取得较好的效果。