邻近算法在微地震震源位置和一维速度模型同时反演中的应用

田宵 汪明军 张雄 张伟 周立

1)江西省防震减灾与工程地质灾害探测工程研究中心(东华理工大学)，南昌 330013 2)南方科技大学，地球与空间科学系，广东深圳 518055 3)中国地震局地震研究所，地震预警湖北省重点实验室，武汉 430071

0 引言

近年来，随着国内外页岩气开采的不断深入，水力压裂技术被广泛地应用于非常规油气藏的开发(张山等，2002；Warpinski，2009；Maxwell，2010)。水力压裂过程中产生的微地震事件可用来监测压裂区域裂缝的发育情况和几何形状、评价压裂效果以及监测诱发地震，因此获得准确的震源位置是微震监测的基础(Grechka，2010；Zimmer，2011)。微地震监测主要包括地面监测和井中监测两种方式(Eisner et al，2010；余洋洋等，2017，朱亚东洋等，2017)。考虑到经济成本和信号质量等因素，单井监测是常见的微地震监测方式，其主要优点在于监测到的微震信号信噪比相比地面监测要高，且定位结果不受近地表的影响。

微地震监测和常规的地震勘探不同，震源的位置和发震时刻均是未知的。因此，微地震定位方法通常借鉴于天然地震领域。目前常用的定位方法有很多种，如基于概率统计的贝叶斯方法(宋维琪等，2013；Zhang et al，2017)、基于走时的震源反演方法(Jones et al，2014；Zhou et al，2015；Tian et al，2016)以及基于波形的定位方法(王晨龙等，2013；Zheng et al，2016；Li et al，2018；田宵等，2020)。井下微震定位通常使用基于走时的定位方法，首先需要拾取微震信号的P波和S波初至，通过找到与初至曲线最吻合的空间位置来进行定位。该类方法主要包括利用绝对到时信息的Geiger经典定位方法(Geiger，1912)、利用走时差反演震源位置的相对定位算法(Waldhauser et al，2000；Guo et al，2017)以及全局的网格搜索方法(Jones et al，2014)。

一般来说，影响微地震单井定位结果的因素主要包括P波和S波到时、检波器方位角和速度模型。其中，速度模型的准确性对定位结果至关重要。在井下监测时，压裂井和监测井之间的距离为200～800m，通常将速度结构简化为一维层状模型。初始速度模型可从声波测井曲线中提取，并利用已知震源位置的射孔事件进行速度校正(Warpinski et al，2005；尹陈等，2013；Jiang et al，2016)，然后进行震源定位。当没有射孔事件时，速度模型可作为未知参数和震源位置同时反演(Li et al，2013；Tian et al，2017)。由于震源位置和速度模型之间有很强的耦合性，基于线性迭代的同时反演方法(本文简称为线性同时反演方法)通常依赖初始模型的选取，反演结果易陷入局部极小值。

近年来，全局反演算法因其不依赖于模型初始值的选择而被广泛应用于微地震速度模型反演。如李志伟等(2006)利用差异算法反演一维速度结构和震源参数；Jansky等(2010)采用邻近算法和网格搜索方法分别更新一维速度模型和震源位置，并使用理论模型加以验证；Tan等(2018)采用改进的邻近算法和主台站方法分别反演一维速度模型和震源位置。

邻近算法(Neighbourhood Algorithm，简称NA)由Sambridge(1999)提出，其是一种解决非线性问题的直接搜索方法，用于在多维参数空间中寻找能够拟合观测数据的模型。该方法在非线性反演问题中应用较为广泛，特别是观测数据和未知参数之间的关系比较复杂的情况(Marson-Pidgeon et al，2000；Sambridge et al，2001)。为了研究邻近算法在微地震单井监测中的可行性，本文采用邻近算法和网格搜索方法分别更新一维速度模型和震源位置(本文简称为邻近算法-网格搜索)。首先通过设计不同层数的理论模型，研究速度模型的层数对邻近算法精度的影响；然后将其应用于单井监测的实际数据中，结合理论分析确定速度模型层数，并将速度模型和震源位置的反演结果与线性同时反演方法进行对比分析。

1 基本原理

1.1 利用网格搜索方法搜索震源位置

网格搜索方法是常用的微地震定位方法，具有简单、快速等优点。首先，需要对可能产生微地震事件的空间进行网格化，网格大小决定着搜索结果的精度以及搜索效率。然后利用射线追踪方法计算每个网格点到检波器的旅行时，最后用计算得到的旅行时与观测到的走时数据进行匹配，误差最小的网格点即最终确定的事件位置。当有大量地震事件需要进行定位时，为了节省计算量，对于给定的速度模型，可将计算的所有网格点到检波器的旅行时保存成走时表，以提高运算效率。

需要搜索的震源参数包括震源位置和发震时刻，为了进一步提高搜索效率，本文使用P波和S波的走时差以及相邻检波器之间走时差消除发震时刻(Zhou et al，2016)，目标函数φ如下

(1)

其中，ns为震源的个数，mr为检波器的个数，上标i和下标k、k′分别代表震源和检波器，向量d为观测的走时数据，G(m)为由模型m正演得到的计算走时。等式右边第一项为每个微震事件的S波和P波的走时差，第二项为检波器之间的P波走时差，第三项为检波器之间的S波走时差。

1.2 利用邻近算法搜索速度模型

邻近算法是一种非导数搜索方法，该方法与遗传算法、模拟退火属于一类，其区别在于模拟退火和遗传算法一般用来解决全局最优解问题，而邻近算法的目的是寻找参数空间中对数据拟合较好的区域进行优先采样的模型集合，而不是寻找单一的最优模型，因此该方法可以更大程度地避免局部最优解。

本文使用Sambridge开源的邻近算法代码(1)http://www.iearth.org.au/codes/NA/，在解决不同的实际问题时，一般需要调节2个参数(nm和nr)来满足不同的采样风格。nm为每次迭代时产生的模型数量，nr为每次迭代时重采样的Voronoi单元的个数。根据Sambridge(1999)，一般nm的大小是参数维数的2倍，nr的范围在2～nm/2之间，且要有足够多的迭代次数。根据经验，迭代次数可设置为nm的10～100倍。毋庸置疑，参数nm和nr的数值越大，就需要更多的迭代次数来寻找准确的解(尤其在搜索参数的数量较多时)。

声波测井曲线可以较好地描绘出岩性分界面，层状模型的厚度可直接从声波测井曲线中提取。为了减少搜索参数的数量，不搜索速度模型的层厚。首先，使用邻近算法产生若干个一维速度模型；然后对于每个速度模型，利用网格搜索方法进行震源定位并计算每个速度模型对应的走时残差；再根据走时残差产生新的速度模型；最后选择合适的迭代次数、nm和nr来保证残差函数收敛到最小值。详细的算法流程如图1 所示。

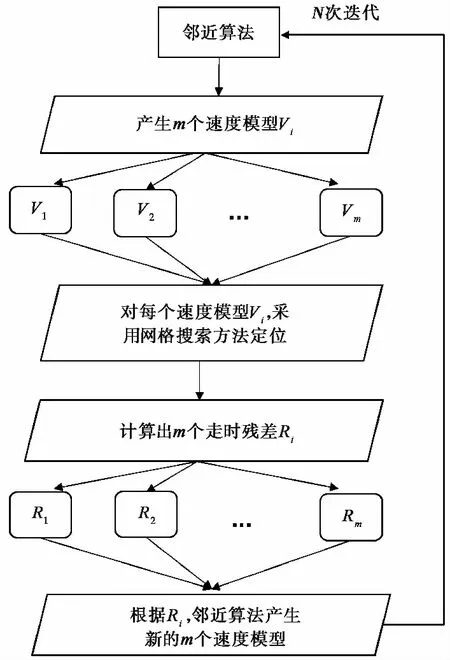
图 1 邻近算法-网格搜索反演速度模型和震源位置的算法流程

2 理论模型计算

一个单井监测的二维理论模型如图2(a)所示，包含4个微震事件(黑色圆圈)和24个检波器(黑色三角形)。速度模型为8层的一维速度模型，邻近算法的搜索范围如图2(b)中阴影区域所示。首先假设每层的纵横波速度比相同，则搜索参数为6，包括5个P波速度和1个纵横波速度比。

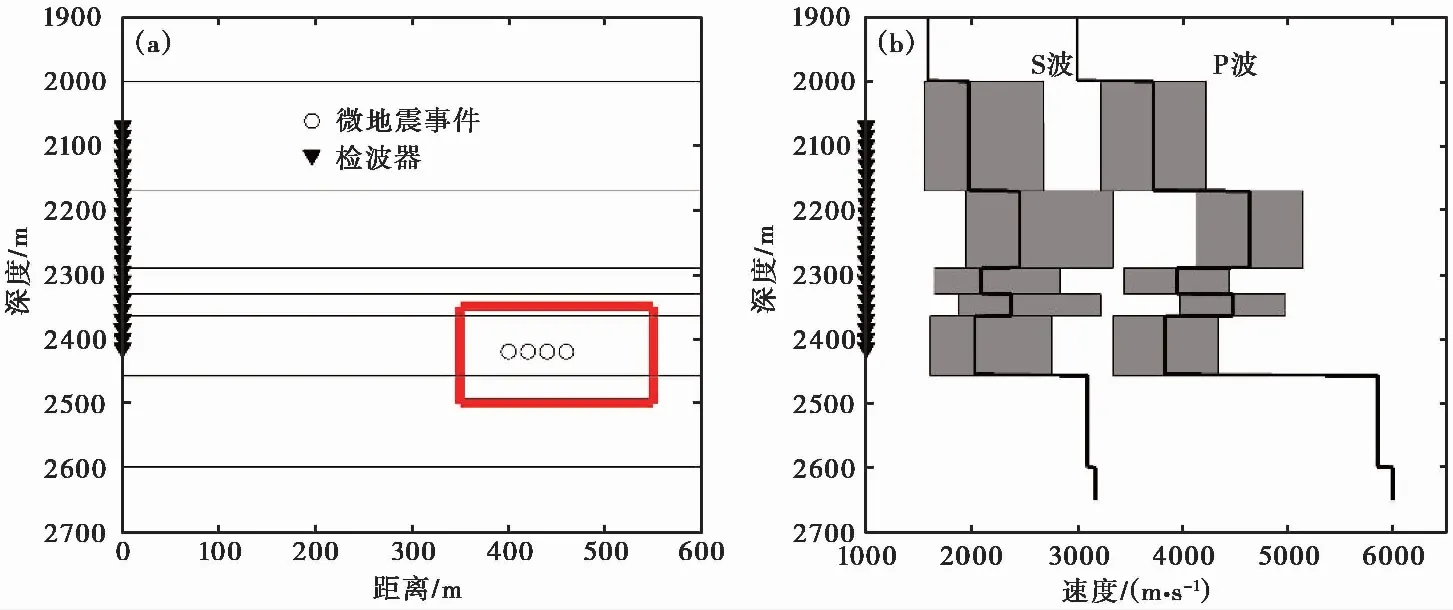
图 2 理论测试模型示意图(a)理论观测系统，红色框为网格搜索范围；(b)一维水平层状模型，灰色阴影区域为邻近算法搜索范围

采用Sambridge提供的邻近算法代码，选取4000个初始样本，nm和nr分别为200和100，迭代次数为500，最后产生了104000个速度模型。网格搜索方法的横向和纵向搜索步长均为2m，搜索范围如图2(a)中红色框所示。反演结果表明在没有噪音的情况下，全局反演方法可以得到真实的震源位置和速度模型。图3(a)为邻近算法-网格搜索方法搜索的前20000个速度模型对应的均方根(Root Mean Square，简称RMS)走时残差，结果表明邻近算法-网格搜索方法经过4000个初始采样点后很快找到正确的采样区域，走时残差降至0.005s以下。最后仅需221次迭代即可搜索到正确的速度模型。

为了模拟实际数据的走时拾取误差，对计算的旅行时添加1ms的随机噪音。反演结果表明当数据有1ms噪音时，震源位置的平均定位误差约16m，搜索过程的走时残差如图3(b)所示。通过对比发现，数据噪声对RMS走时残差有一定的影响，对搜索过程的收敛速度影响较小。为了更加清楚地展示搜索过程中产生的速度模型，图4 给出了数据有噪音时邻近算法-网格搜索方法搜索的前20000个速度模型，速度模型的颜色越接近红色，代表RMS走时残差越小。由图4 可见，数据有误差时，搜索的速度模型也有一定偏差。

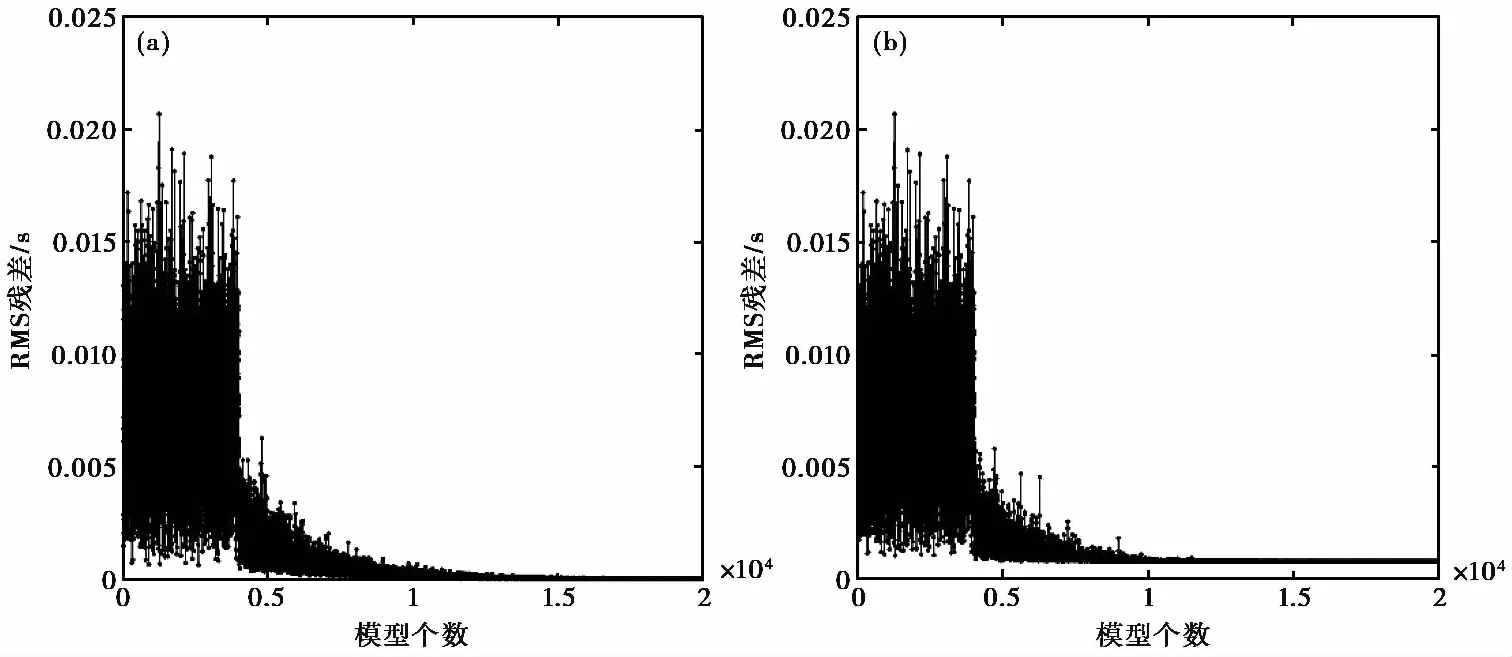
图 3 邻近算法-网格搜索方法在没有噪音(a)和有噪音(b)时的走时残差分布

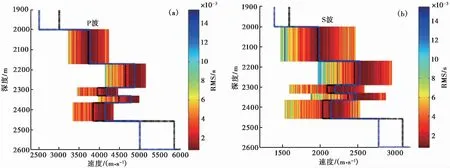
图 4 数据有噪音时邻近算法-网格搜索方法反演的P波(a)和S波(b)速度模型黑色虚线为真实速度值；蓝色虚线为最终反演结果

以上理论测试中固定了纵横波速度比，降低了搜索维度。但是实际情况的纵横波速度比与泊松比有关，不同的岩石类型其纵横波速比有所不同，除了一些特殊的岩石，纵横波速度比的范围在1.5～2.2之间。在处理实际数据时，很难将每层的纵横波速度比当成固定值。对于一个n层的速度模型，搜索参数的个数应为2n。因此，讨论搜索参数的数量对反演结果准确度和收敛性的影响是非常有必要的。图5 给出了搜索参数的数量和RMS走时残差的关系，为了更好地研究参数数量对反演精度的影响，图中未对走时信息添加噪音。每个搜索参数均根据Sambridge(1999)给出的经验调节nm、nr以及迭代次数。图5 表明反演结果的RMS走时残差随着搜索参数的增加而急剧上涨。当搜索参数等于14时，对应的走时残差量级为 10-4s。 因此，在利用邻近算法-网格搜索方法反演一维速度模型时，应尽可能地减少速度模型的层数。

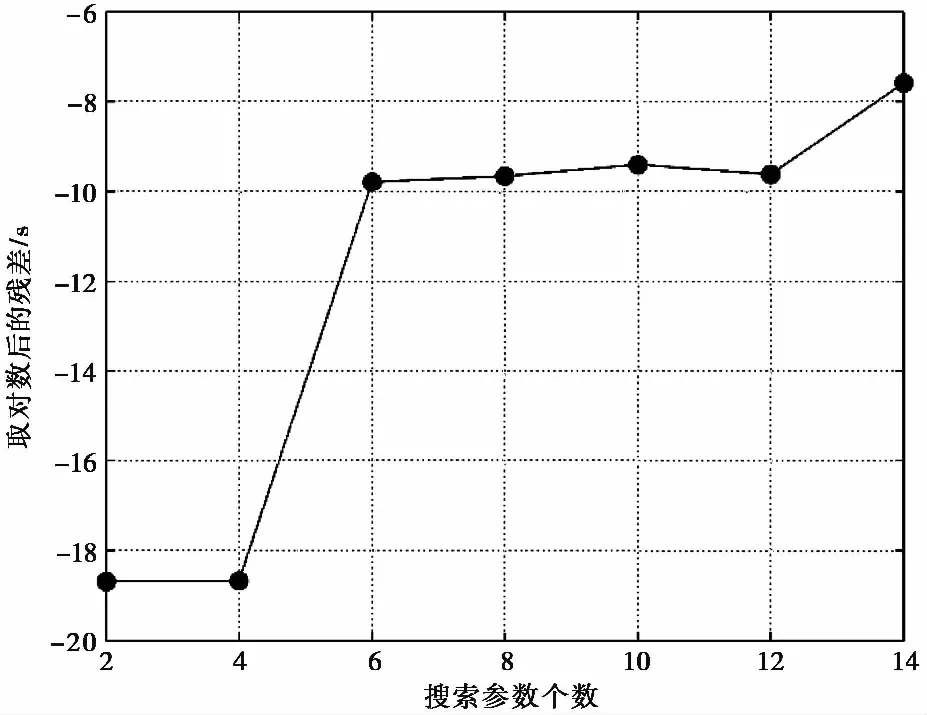
图 5 不同的搜索参数数量对应的走时残差

3 单井监测的实际数据

将邻近算法-网格搜索方法应用于单井监测的水力压裂实际数据中，该套数据为水平井压裂、垂直井监测。监测井中包含了12个三分量检波器，深度2800～3020m，间距20m。为了验证邻近算法-网格搜索方法的结果，对该套数据进行了线性同时反演，线性同时反演算法需要初始速度模型和初始震源位置。图6(a)中灰色实线为声波测井曲线，为了减少邻近算法-网格搜索方法搜索参数的个数，本文从中提取了一个包括P波和S波的五层初始速度模型(黑色实线)，图6(a)中黑色三角形为检波器的深度位置。考虑到检波器和压裂井所在区域，图6(b)中灰色区域为邻近算法-网格搜索方法搜索的速度范围，搜索参数的个数为8。

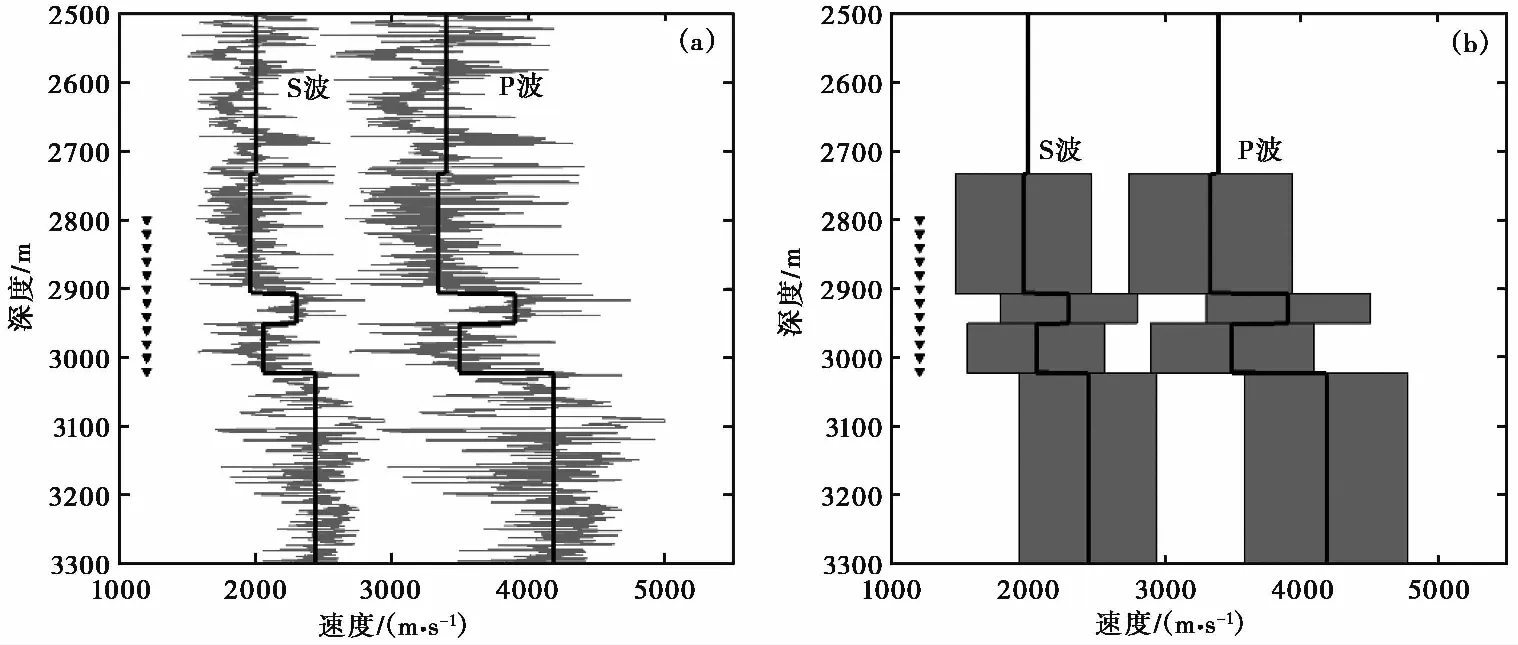
图 6 实际数据速度模型(a)测井曲线以及提取的初始速度模型；(b)邻近算法-网格搜索方法搜索的速度范围(灰色区域)

在第18个压裂段选取40个信噪比较高的微震事件，并手动拾取了P波和S波到时。考虑到一维速度模型和垂直监测井的对称性，将所有的地震事件投影到一个垂直平面(XZ)，将三维的定位问题简化为二维，垂直平面包括一个垂直的Z坐标和一个水平的X坐标(事件到监测井的距离)。随后在二维平面上进行定位，并利用事件的方位角将定位结果反投影回三维空间，事件的方位角可由P波偏振分析确定。

分别用线性同时反演算法和邻近算法-网格搜索反演震源位置和一维速度模型。对于该套数据，根据Sambridge(1999)的算法，选取1000个初始样本，nm和nr分别为20和10，迭代次数为200，邻近算法最终会产生5000个速度模型。图7(a)为邻近算法-网格搜索方法得到的所有速度模型对应的RMS走时残差，结果表明200次迭代足以得到稳定的结果，最优的速度模型为第4947个，如图7(b)中红色虚线所示，对应的走时残差为1.64×10-3s。表1 对比了不同的邻近算法参数得到的RMS走时残差，结果表明增加搜索样本数或者更改速度模型的搜索范围对反演结果的影响不大。

图 7 邻近算法-网格搜索反演结果(a)邻近算法-网格搜索方法得到的速度模型对应的RMS走时残差；(b)速度反演结果，黑色实线代表初始速度模型，红色虚线为邻近算法-网格搜索方法反演的结果，蓝色虚线为以交替反演结果为初始值的线性同时反演结果

表 1不同的邻近算法参数对应的RMS

对于线性同时反演方法，一般采用测井曲线提取的速度模型为初始速度模型(图6(a)中黑色实线)，网格搜索结果为初始震源位置。采用不同方法对40个微震事件进行定位，结果如图8 所示，其中包括X-Y平面和X-Z平面。进行水力压裂作业时，微地震事件一般发生在压裂段的附近，而网格搜索的定位结果(图8 中绿色点)在深度上与压裂井相差100m左右。以网格搜索的结果为初始值进行线性同时反演，得到的震源位置如图8 中紫色点所示，对应的走时残差为2.91×10-3s。从X-Z平面上来看，绿色点和紫色点的分布相似，均在压裂井的下方。图8 中红色点为采用邻近算法-网格搜索得到的定位结果，可以看出微震事件分布在压裂井的两侧，反演结果较为合理。进一步对比邻近算法-网格搜索方法(红色点)和线性同时反演方法(绿色点)的定位结果和走时残差，结果表明2种方法的定位结果在水平方向上相似，深度上差别较大。而线性同时反演的深度与初始位置相似，由此可推断出，以网格搜索结果为初始值的线性同时反演方法可能陷入局部最优解。此外，本文还采用Tian等(2018)的反演流程，首先利用交替迭代方法得到一个较好的初始解(包括震源位置和速度模型)，再采用线性同时反演方法，定位结果如图8 中蓝色点所示，速度反演结果为图7(b)中蓝色虚线，走时残差为1.74×10-3s。对比邻近算法-网格搜索方法(红色点)和以交替迭代为初始值的线性同时反演(蓝色点)结果，可以看出2种方法得到的定位结果均较为合理。线性同时反演方法容易陷入局部最优解的主要原因为，微地震实际数据资料的信噪比较弱以及单井监测的检波器分布范围较小，导致震源位置和速度模型之间存在较强的耦合性，求解空间存在多极值问题。因此，线性同时反演依赖初始值的选取，一个好的初始值有助于线性同时反演方法跳出局部最优解。

图 8 40个微震事件的定位结果绿色点为网格搜索的结果；红色点为邻近算法-网格搜索算法的结果；紫色点和蓝色点分别为线性同时反演方法以网格搜索和交替迭代为初始值的结果

为了进一步评价速度模型和震源位置反演的精度，给出了2种方法反演的40个微震事件的走时拟合残差分布直方图，见图9。走时拟合残差为反演结果(震源位置和速度模型)正演的理论走时与拾取走时之间的偏差。图9 中“同时反演1”为线性同时反演方法使用网格搜索的震源位置和测井速度为初始值时得到的走时残差分布，而“同时反演2”为线性同时反演方法使用交替迭代结果为初始值时得到的走时残差分布。通过对比，“同时反演1”、“同时反演2”和邻近算法-网格搜索方法分别有49.8%、75.0%和74.8%的P波走时残差分布在0～1ms范围内，而3种方法的S波走时残差分别有28.6%、56.1%和58.0%的事件分布在0～1ms范围内。对比走时残差的平均值，“同时反演1”、“同时反演2”和邻近算法-网格搜索方法的P波走时残差平均值分别为0.0012、7.65×10-4和7.62×10-4，而S波走时残差的平均值分别为0.0021、0.0011和0.0011。因此，当线性同时反演使用较好的初始值时，得到的走时残差分布与邻近算法-网格搜索的结果大致相同。

图 9 线性同时反演方法和邻近算法-网格搜索方法的走时残差直方图(a)和(d)分别为线性同时反演方法使用网格搜索为初始值的P波和S波走时残差分布；(b)和(e)分别为线性同时反演方法使用交替迭代结果为初始值的P波和S波走时残差分布；(c)和(f)分别为邻近算法-网格搜索方法的P波和S波走时残差分布

上述结果表明，与线性同时反演方法相比，邻近算法-网格搜索方法受初始模型影响较小，能够最大限度地避免局部最优解。虽然该方法能够从局部最优值中跳出，但其缺点为计算量较大。对比线性同时反演和邻近算法-网格搜索方法在不同微地震规模下的计算时间(表2)，可以看出线性同时反演的计算效率远远高于邻近算法-网格搜索方法。值得注意的是，随着反演的微震事件个数的增加，线性同时反演方法所需的计算量几乎成倍增长，而邻近算法-网格搜索方法增长速度较慢。这是由于随着微震个数的增加，线性同时反演需要求解的反演方程组也相应变大，而邻近算法-网格搜索方法只在震源定位时增加了定位个数。因此，当实际数据中存在成百上千个微地震事件时，邻近算法-网格搜索方法的适用性较强。

表2两种方法的计算效率对比

4 结论

本文研究了微地震单井监测情况下，利用邻近算法-网格搜索方法反演震源位置和一维速度模型的可行性。主要讨论了理论数据在有噪音和无噪音时的反演结果，以及搜索模型参数的数量对邻近算法-网格搜索方法精度的影响。结果表明该方法具有较强的收敛性，但随着模型参数的增加，反演误差迅速上涨且计算量增加。为了验证邻近算法-网格搜索方法在实际数据中的应用效果，将反演结果与线性同时反演结果对比，结果表明线性同时反演对初始值的依赖性较强，容易陷入局部最优解，而邻近算法-网格搜索方法受初始值的影响较小，得到的震源定位结果分布在压裂段附近，较为合理。

致谢：感谢东方地球物理公司提供的水力压裂监测数据以及审稿人提供的宝贵评阅意见。