电缆故障测距的模型仿真与系统设计

金增杰，卫永琴，张琦，王潇龙

（1.山东科技大学电气与自动化工程学院，山东 青岛 266590；2.国家电网山东省电力公司检修公司，山东 济南 272000）

目前，全球用电量增长迅速，我国作为能源大国对电能的利用远超其他国家[1]，这就要求我国的输配电系统具有较高的运行可靠性及持续稳定性[2-3]。而输电线路上的电线电缆有如下优点[4]：1）具有外护层，使得电缆芯线使用寿命长；2）电缆一般埋于地下，不占地上面积，自然也不会有影响环境美观的问题。但同时也带来了一些实际问题，最明显的是其在地下，走线复杂曲折，一旦发生故障，很难定位故障点，并且长时间的停电检修，浪费人力物力，对社会生产和经济都会造成较大的损失[5-6]。那么如何迅速准确地找到故障点位置已经成为了研究的热点问题。

故障测距主要是为了快速发现故障点，这样工作人员就可以及时排除故障和修复线路，所以我们研究的首要问题是如何在最短时间内把故障范围缩小到最小。现有的电缆故障测距方法主要分为离线和在线测距两种[7]。离线测距是我国目前主要的电缆故障测距方法[8-9]。而行波法是研究最多的一种离线测距法，已有的故障测距的计算公式均与故障点相位有关，不易实现。本文推导出了易操作的测距计算公式，采用多频测相法在Matlab平台上仿真并验证。最后设计了电缆故障测距硬件系统，完成调试并通过实验对系统可行性进行了验证。

1 电缆故障行波等效模型

下面研究行波在电缆故障中传播的等效模型，在工程计算中，假设行波传播速度的经验值等于行波的真实传播速度[10]。

图1为行波在故障电缆中传播的示意图，电缆两端点分别用h和i表示，f为电缆中出现的故障点。信号Vh从h端进入电缆，当其到达f点时，便会产生折射和反射。Vfh为反射信号，从f点往回传播到端点h；Vfi为折射信号，向前传播至端点i。

图1 故障电缆行波传播示意图Fig.1 Traveling wave propagation schematic of fault cables

下面建立电缆故障行波传播的数学模型，假设X1为原始信号，其表达式为

式中：H为信号幅值；ω为角频率；t为传播时间；θ为初始相位。

测试信号在电缆中传播时，到达故障点产生的反射信号Xfh与电缆首端的输入信号Xfi叠加，用X2表示如下：

X2(t)=H0sin(ωt+θ)+H1sin(ωt+θ+φ)（2）

式中：H0为注入信号幅值；H1为故障点反射信号的幅值；φ为反射信号Vfh和折射信号Vfi的相角差。

2 推导测距公式及相位差计算

相位法测距是基于行波测距原理提出的一种间接测距方法，测距基本公式为

式中：λ为正弦信号的波长；N为信号在入射点和故障点之间完整传播的次数；Δφ为不足1个周期的相位差；2π为1个完整的传播周期。

多频测相法是一种依据电缆总长来逐步增加信号频率的测距方法，这种方法可以使测距更精确。根据已有文献的研究可知，电压的折射和反射系数都会受到频率大小的影响[11]。下面针对断路和短路两种情况，推导出不同的测距公式。因断路时故障信号具有正的反射系数[12]，φ的取值范围为0～2π，则测距公式可以表示为

短路故障时，信号的反射系数为负[12]，φ的取值范围为-π～π，测距公式为

定义入射信号为X1，经故障反射后的叠加信号为X2，对比信号为X3。令X1与X3频率相同，均为ω。令X1的初相位为0，则X2，X3两信号经过乘法器运算之后，再通过低通滤波器将高频信号过滤掉，得到输出信号：

为了计算简便，设定信号X3的初始相位θ分别为0和π/2，得到φ的表达式为

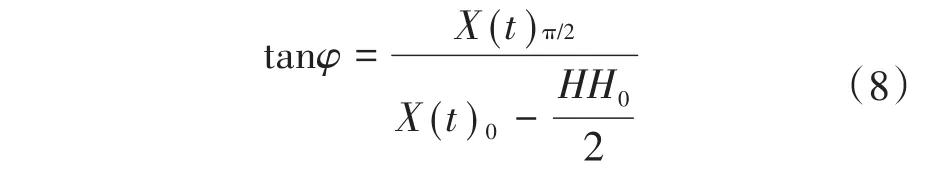
式中：Xπ/2为θ=π/2时X（t）的值；X0为θ=0时X（t）的值。

通过tanφ的值即可求出所需相位差。

3 Matlab建模仿真分析

通过Matlab/Simulink搭建电缆故障模型，首先依据实际情况对电缆参数进行设定，然后通过多频测相原理和相位法对电缆故障进行仿真分析，模型如图2所示（只进行了A，B相电缆检测）。

图2 电缆故障模型Fig.2 Cable fault model

图2中，受控电压源接收正弦波信号，分别作为检测的入射信号X1和对比信号X3，X1通过电阻模块注入电缆，电缆分布参数设置如表1所示。

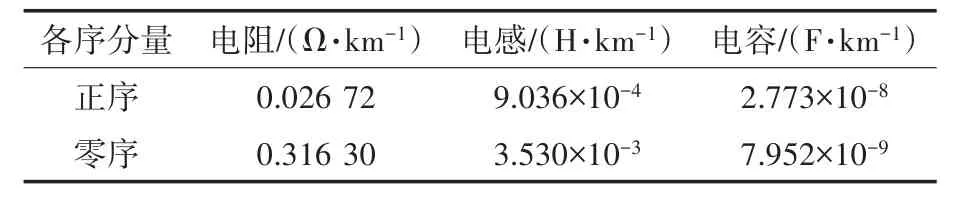
表1 电缆分布参数Tab.1 The parameters of the cable distribution

3.1 短路故障

首先，设置电缆总长度S为23 km，A段长度即故障距离为17.65 km，故障设为接地电阻为10 Ω的单相接地故障。采样频率fs=100 MHz，采样时间t=0.005 s。信号1和信号2的幅值均为5 V，X1的初相位为0，由此可得入射信号X1，叠加信号X2以及对比信号X3。

然后，1）根据电缆长度选择4个测距信号的频率f1～f4，要求满足λ＞2S且留有一定裕度，取波长λ1=50 km，假设选择的第一频率f1=3.993 8 kHz，确定故障距离的十位数字；2）确定故障距离的个位数字，此时λ2/2=10 km，f2=9.967 kHz；3）确定故障距离小数点后第1位数字，此时λ3/2=1 km，f3=99.67 kHz；4）确定故障距离小数点后第2位数字，此时λ4/2=0.1 km，f4=996.7 kHz。

f1=3.993 8 kHz时，可以得到θ=0和θ=π/2两种情况下示波器V4的波形，如图3所示。

图3 短路故障f1=3.993 8 kHz时V4波形Fig.3 V4waveforms at f1=3.993 8 kHz when short circuit fault

图3中高频分量被滤掉，只剩直流分量，X0=1.991 V，Xπ/2=-4.528 V，可得tanφ=7.114，相位差φ为-0.544π或0.456π，由于故障反射信号Vf总滞后于由电压测量元件1测得的发射信号VM1，因此φ的值为正，取φ=0.456 π，故障类型为短路故障。根据式（5）可得故障距离S1=18.2 km，因此故障距离十位数字为1。此时误差为0.55 km，相对误差为2.391%。运用同样的方法可分别计算出其他3个频率测距时故障距离的个位、小数点后第1位和小数点后第2位数字，最终得到故障距离S4为17.613 2 km，误差为-0.036 8 km，相对误差从第1个频率测距时的2.391%精确到了0.16%。

为了进一步验证该方法测距的准确性，分别设置故障距离为2.59 km，9.68 km，13.24 km，17.32 km和22.05 km。仿真结果如表2所示，其中，S为测量的故障距离，e为相对误差。

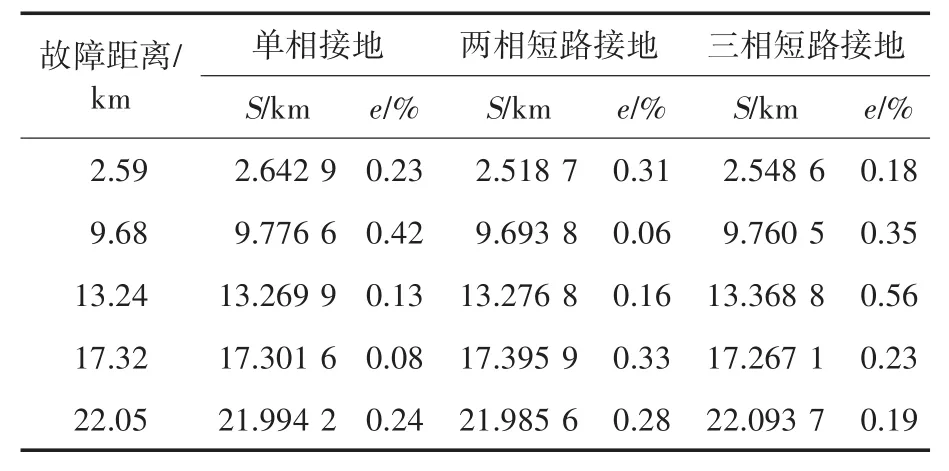
表2 短路故障仿真结果Tab.2 Simulation calculation results when short circuit fault

3.2 断路故障

将故障类型设置为A相单相断路，采样时间t=0.005 s，采样频率fs=100 MHz。由于故障距离没有改变，因此四组测量频率与短路故障时相同。f1=3.993 8 kHz时，可以得到θ=0和θ=π/2两种情况下示波器V4的波形如图4所示。

图4 断路故障f1=3.993 8 kHz时V4波形Fig.4 V4waveforms at f1=3.993 8 kHz when open circuit fault

由图4可知，X0=1.996 V，Xπ/2=-4.529 V，同短路故障相同，利用式（8）可以求出tanφ=7.171 8，所以相位差φ=0.456π或 1.456π，因为Xπ/2＜0，而φ∈(π～2π），可得φ的值为1.456π，利用式（4）可得故障距离S1=18.2 km，故障距离十位数字为1，计算可得误差为0.55 km，相对误差为2.4%。同样的方法可得到其他3个频率测距时测量故障距离的个位、小数点后一位和小数点后第二位数字。最终计算出故障距离为17.726 6 km，误差为0.076 6 km，相对误差从第一个频率测距时的2.4%精确到了0.33%。

同样，分别设置故障距离2.59 km，9.68 km，13.24 km，17.32 km和22.05 km，仿真计算结果如表3所示。

表3 断路故障仿真结果Tab.3 Simulation calculation results when open circuit fault

依据以上结果可知，当电缆故障发生在不同的距离时，此方法不受故障类型的影响，能检测出准确的故障距离，误差不超过0.6%。

4 系统设计及实验

4.1 系统总结构

根据以上的公式推导和仿真结果理论分析，设计了一种多频测相法电缆故障测距系统，如图5所示。

图5 多频测相法电缆故障测距系统Fig.5 Ranging system with multi-frequency phase method when cable fault

本文提出的多频测相法电缆故障测距系统工作原理如下：首先将故障数据输入系统，中央处理器检测信号频率有无超出临界值，若低于临界值便通过信号发生器发出两个频率同步的信号，分别输入电缆首端和乘法器中，进入电缆的信号到达末端再次沿电缆返回后同样注入乘法器。之后乘法器输出信号，通过低通滤波器处理该信号变为直流，最后通过A/D转换器将信号输入中央处理器。第一频率完成运行计算之后，中央处理器自主选取下一频率，继续重复上述过程，最终由上位机显示距离数值。

4.2 系统组装及实验测试

系统包括STM32系统、信号发生器AD9959及2个运算放大器、2个功率放大器、1个乘法器和1个4阶巴特沃斯低通滤波器等，组装焊接并调试。

下面利用这套测距系统做实验，实验中的电缆绝缘材料为聚氯乙烯，选其波速为130 m/µs，将电缆在1 km处断开，也就是断路故障。将入射信号的幅值设置为5 V，并注入电缆；将对比信号的幅值设置为2.5 V，并注入乘法器。运行系统，根据系统提示向下位机发送电缆长度和故障类型（0表示短路故障、1表示断路故障），随后系统会根据电缆故障信息自动选择频率进行测距，如图6所示。

图6 测距结果Fig.6 Ranging result

第一频率为66 kHz，分别设置对比信号的相位θ为0和π/2，用示波器观测相应的滤波器输出直流信号X0和Xπ/2，如图7所示.

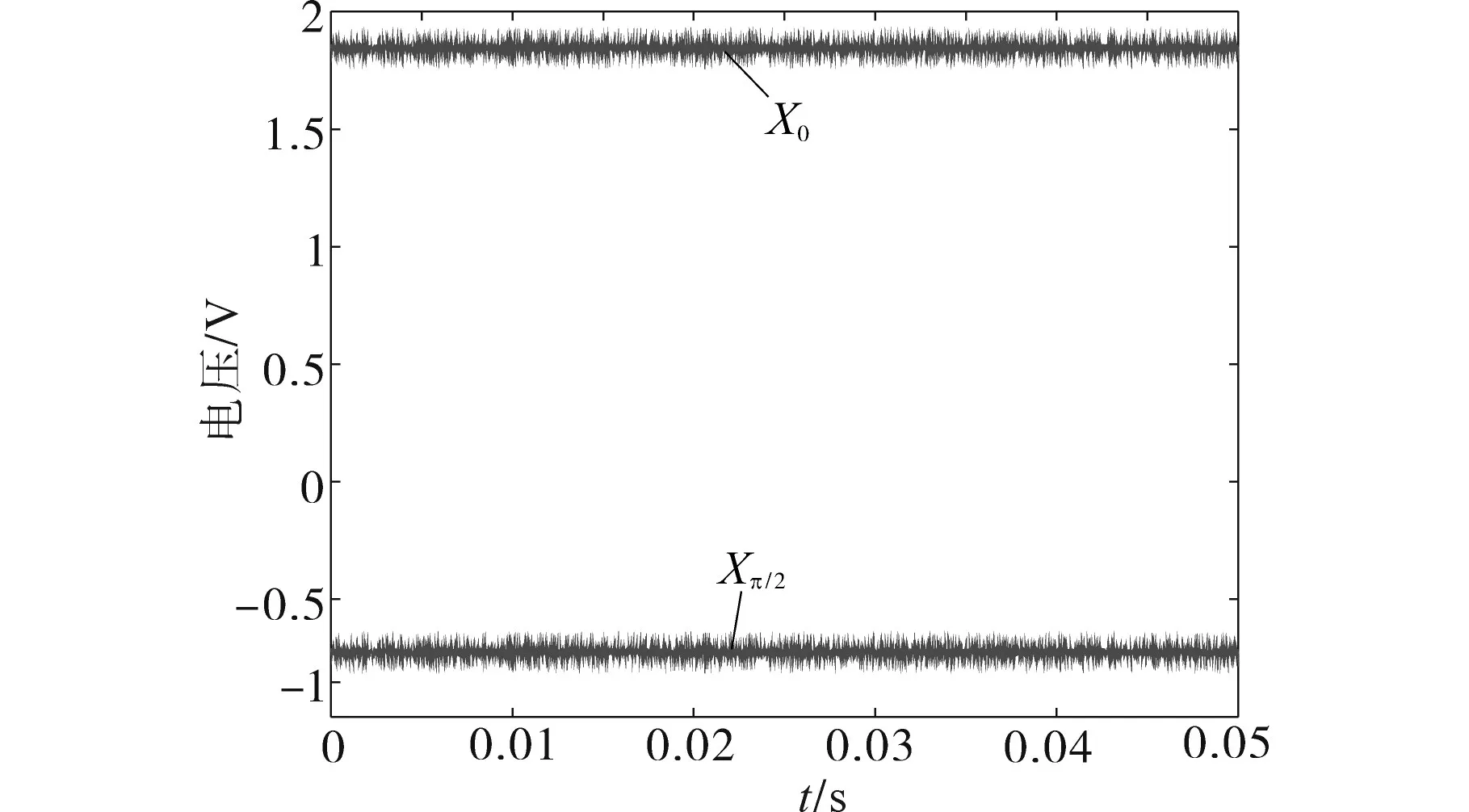
图7 第一频率为66 kHz时的直流分量Fig.7 The DC components at the first frequency of 66 kHz

图7中直流分量X0的值为1.93 V，直流分量Xπ/2的值为-0.8 V，可以计算出X0的初始值为6.655 V，Xπ/2的初始值为-2.759 V，相位差φ为1.843 6π或0.843 6π，最后算得故障距离为0.921 8 km，与系统运行结果一致。

第2次选频后的直流信号中直流分量X0=1.053 V，直流分量Xπ/2=-0.4 V。经计算可知故障距离为0.990 8 km。

将电缆末端设置为短路，通过本系统测距得到的故障距离为0.997 6 km。通过以上结果可知，该测距系统能够根据设计方案测量故障距离，测得的断路故障和短路故障相对误差分别为0.92%和0.24%，符合预期目标。

5 结论

本文通过多频相位法对电缆故障测距进行研究，推导出短路故障和断路故障下不同的测距公式，然后用Matlab建立电缆故障模型并利用多频测相的相位法测量故障距离。

通过仿真结果分析可知，本文提出的多频相位对电缆故障测距方法，可测得故障距离，且误差均小于0.6%，充分论证了此方法的可行性，同时此测距方法具有不受故障点位置和故障类型的影响的优越性。

但是因为条件不足，系统虽能完成测距，但设计上依然存在有待改进之处：

1）存在部分元件带宽不足的问题，限制了频率的选取。

2）系统只根据线路绝缘材料选择了一种行波速度，如果通过频率的差异设置不同的波速会进一步提高测距的精度。