人工神经网络预测并行查询响应时间

刘冬燕，牛保宁+，张锦文

(1.太原理工大学 信息与计算机学院，山西 晋中 030600；2.北方自动控制技术研究所 软件研发部，山西 太原 030006)

0 引 言

数据库管理任务依据查询响应时间，结合系统优化配置的目标，选择下一步要执行的任务，为数据库的性能管理提供决策支持[1]。查询响应时间由使用资源时间和等待资源时间[2]组成，详述查询执行过程的查询计划决定了查询使用资源的时间，并行运行查询会产生查询交互[3-5]，直接影响查询等待资源的时间。因此，对查询响应时间建模应将查询计划、查询交互纳入考虑。

经过数十年的研究，查询响应时间预测模型按建模理论可分为：分析模型和统计模型[6]。分析模型简化资源争用降低复杂度，使得模型预测准确率较统计模型低[7]。现有统计模型将查询交互信息映射成查询响应时间，采集样本训练预先确定好的模型函数，其预先确定的模型函数限制了对样本的拟合精度，该模型仅对查询交互进行拟合忽略了查询本身所具有的信息，多数统计模型无法应对训练集中未出现过的查询。人工神经网络无需预先确定模型函数，通过对样本集自学习来拟合模型函数[8,9]。现有人工神经网络仅能预测单个查询的响应时间，而典型的工作负载包含多个查询并行运行。根据对数十年查询响应时间相关文献的研究可知，当前数据库领域还没有研究者提出使用人工神经网络模型预测并行查询响应时间。

联机分析处理(online analytical processing，OLAP)系统通过对数据的多维分析为决策提供依据，需周期性地批量运行固定查询。本文以OLAP系统这一特定场景为对象，针对统计模型存在的问题，结合查询计划、查询交互两大要素，研究用全连接神经网络预测并行查询响应时间。

本文的主要贡献如下：

(1)提出用全连接神经网络预测并行查询的响应时间。采用全连接神经网络，训练网络建立模型，进行预测；

(2)采用查询计划特征分量描述查询的资源需求、查询交互特征分量描述查询之间的资源争用，共同构成神经网络的输入特征向量；

(3)本文所提全连接神经网络模型可实现对并行查询响应时间的动态预测，直接抽取包含新查询查询组合的查询计划特征、查询交互特征，输入到模型中实现动态预测。

训练好全连接神经网络后，进行了多组模型预测的实验，结果表明全连接神经网络模型预测准确率优于代表性统计模型，一定程度上说明了全连接神经网络模型的可行性。

1 相关研究

1.1 查询响应时间预测模型

现有查询响应时间预测模型分为：分析模型与统计模型。

分析模型建立在数据库成本模型之上，结合查询计划所涉及到操作工作量转化为查询的响应时间。并行分析模型中，并行运行的查询存在查询交互导致建模过程复杂，而现有的研究丢弃了查询的部分特征，使得模型预测准确率较统计模型低[2]。

统计模型预先确定数学模型函数，通过采集样本对模型函数进行训练。并行查询响应时间预测中，最为代表性的统计模型是张锦文等提出的相似性模型[2]，对查询交互进行量化分析并在此基础上建立相似性模型。该模型从查询响应时间的样本库中选取包含该查询的K个组合的响应时间，取均值作为目标查询的响应时间。与分析模型相比，统计模型建模不需要分析查询计划及其涉及到的操作，通过采集样本对统计模型函数进行训练得到模型、进行预测。模型预测准确率较高，但是统计模型缺点在于，不知道预先确定的模型函数是否适合样本，使得模型准确率无法提高。

循环神经网络模型[10]按建模理论来讲属于统计模型的一种，但不同于一般的统计模型，不需要提前设定模型函数，仅对样本集学习就能建立模型,但该模型仅对单个查询响应时间进行预测，实用性低。

1.2 模型特征的提取

不同的模型需要选取不同的特征与之匹配。分析模型、循环神经网络模型均对查询计划进行分析，模型特征细化到查询操作符。

统计模型仅拟合查询交互，选取查询交互信息作为特征。相似性模型用QueryRating[2,11]来度量查询交互。并行程度大于2时，根据查询受到的直接影响、间接影响将所涉及到的QueryRating特征压缩成二维特征。

分析模型提供了一个白盒视角，显示地表达数据库系统的工作机制；统计模型提供了一个黑盒的视角，隐式地表达了查询交互的影响。

1.3 模型动态性

在分析模型中，如果出现新查询，为适应该查询，则所有对查询的估计值都将频繁发生变化[9]，导致估计不准确。并行分析模型随着并行程度的增加，管道数量剧增，由于查询交互每个管道的成本须做相应调整，建模复杂度高，使得模型可用性降低，甚至变得不可用。

目前，实现并行查询响应时间预测的统计模型主要有线性模型、高斯交互模型、适应性交互模型、B2L模型、相似性模型。除相似性模型之外，其余模型仅能实现对已有查询的预测，无法应对训练集中未出现过的查询，动态性差。

2 问题与方法

数据库系统中，查询不断地进出，一个查询可能会包含在多个查询组合中运行完成，对查询响应时间的预测只能是对查询在当前所处的查询组合中持续运行到结束的时间。当查询组合发生变化，查询响应时间需要做出更新。本节针对上述问题分两步完成：对固定查询组合中每个查询响应时间进行预测；基于固定查询组合动态实现可变查询组合中查询响应时间预测。第2.1节详细介绍上述问题并提出解决思路，第2.2节介绍全连接神经网络模型的相关知识，第2.3节、2.4节分别对固定查询组合、可变查询组合下查询响应时间的问题进行定义并提出解决方案。表1是对本文所涉及到主要概念的说明。

表1 相关术语描述

2.1 问题与解决思路

数据库系统中，并行运行的查询在执行过程中，一些查询结束执行，新的查询进入，查询组合不断改变，同一查询的运行过程可能会经历多个不同查询组合。由于查询的进出是未知的，因此，这里对查询响应时间的预测是指：某一时刻，查询在当前组合中运行到结束的时间，再加上查询已经运行的时间。如图1所示，T1时刻，查询1结束，查询2进入，与查询5、查询3组成新查询组合(5，2，3)。查询5经历(5，1，3)与(5，2，3)两个查询组合，其响应时间等于这两个组合中查询5的运行时间和。

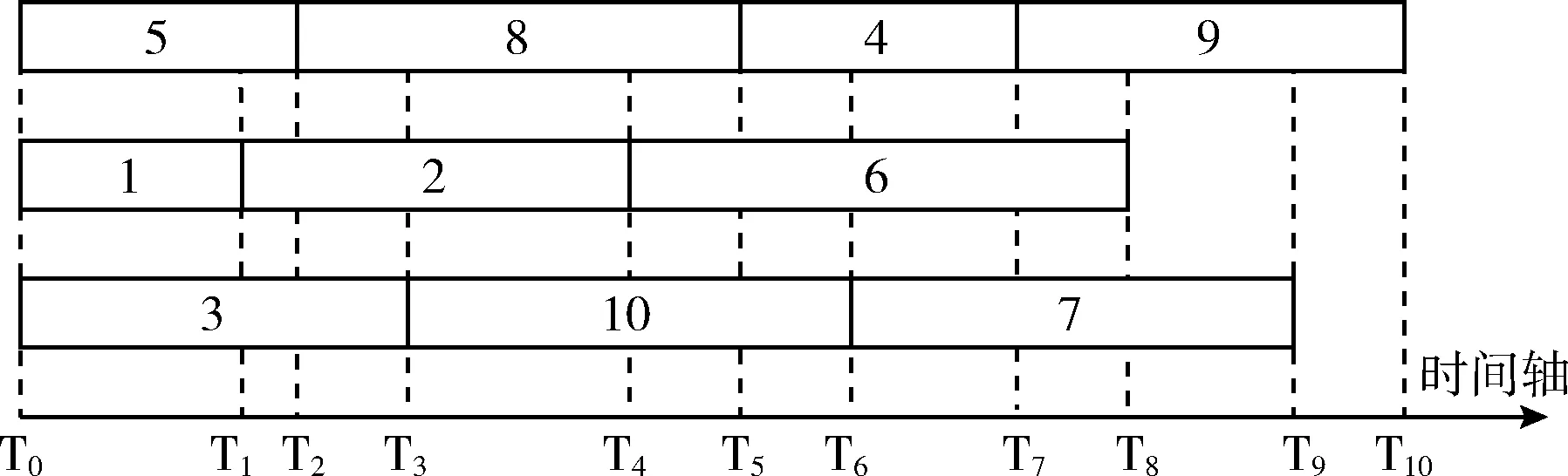
图1 3个查询并行运行示例

查询在当前组合中从开始一直运行到结束的时间，本文称之为查询在固定查询组合中的响应时间。T1时刻，对查询5的响应时间预测由两部分组成：查询5在组合(5，2，3) 中运行到结束的时间T2-T1，查询5在组合 (5，1，3) 中已经运行的时间T1-T0。查询5实际在组合(5，2，3)中的运行时间T2-T1是它在固定查询组合 (5，2，3) 中的响应时间，减去它在组合(5，1，3)中已完成工作的时间。这要求计算查询在前面组合中所完成工作占整个工作的比例。

数据库系统中，查询的执行速度是复杂多变的，精确计算查询在已经历的组合中所完成工作占整个工作的比例需要为查询执行速度建模，并非易事，不在本文的讨论范围。为了实现对并行查询响应时间的预测，本文假设查询的执行速度是匀速的。假设查询5在固定查询组合(5，1，3)、(5，2，3)的响应时间已知分别为t、t1， (T1-T0)/t得出查询5在固定查询组合(5，1，3)完成的工作量， 1-(T1-T0)/t 计算出查询5未完成的工作量即，查询5在查询组合(5，2，3)需要执行的工作量， (1-(T1-T0)/t)*t1得出T1时刻查询5的剩余运行时间。通过对查询5响应时间的分析，可知查询响应时间的预测需分两步实现：第一，完成固定查询组合下查询响应时间的预测；第二，在实现固定查询组合预测的基础上，估计查询的剩余工作量，实现对可变查询组合预测。

进行预测之前，我们需要对全连接神经网络进行设计。

2.2 全连接神经网络

2.2.1 网络结构设计

建立全连接神经网络需要确定网络层结构、输入特征、预测标签、超参数。层结构的关键在于隐藏层的层数，增加隐藏层会使得训练时间延长且容易出现过拟合，一般情况下，优先选用只有一个隐藏层的网络，通过增加节点数来降低误差；George Cybenko证明仅有一个隐藏层的人工神经网络，通过增加节点数能够逼近任意函数。因此，本文采用只有一个隐藏层的网络，如图2所示。输入层由QPF、QIF共同组成，其输入节点数为10 425(详见2.2.2节)。

图2 网络结构

2.2.2 输入特征、预测标签设计

本文采集查询计划相关操作与查询交互数据共同作为全连接神经网络模型的输入特征。查询组合的输入特征设计为QPF、QIF。

QPF是一个查询的查询计划构成的特征。查询中的每个操作由以下4部分组成：操作的类型、操作涉及到的表、列以及结果行的平均宽度[11]。其中，操作的类型，例如Seq Scan、Hash Join等，本文所用的PostgreSQL数据库共有34种操作类型，将操作对应类型的位置置1，其余为0；操作涉及到的表，TPC-H[12]中共有8张表，涉及到的表对应位置置1，其余为0；操作涉及到的列共有61个，对应位置置1，其余置为0；操作涉及到的结果行的平均宽度划分20个区域，区域间隔10，操作涉及到的宽度对应位置置为1，其余为0。本文选取的查询模板最多含有25种操作，每个操作信息包含123位分别是34个操作类型、8张表、61个列、20个结果行平均宽度之和。经计算，一个含有25种操作类型的查询共有3075位。

QueryRating是查询两两并行运行时的响应时间与单独运行响应时间的比值，可用如式(1)所示

ri/j=ti/j/ti

(1)

式中：ti/j表示查询i与j并行时，i的响应时间；ti表示查询i单独运行时的响应时间；ri/j则是对查询i的量化值，反映查询之间资源争用的强弱程度，当ri/j>1 说明查询i与查询j存在资源竞争关系，反之说明查询i与查询j存在资源合作关系。

QIF是一个查询受其它查询影响的QueryRating值所形成的组合。实验统计QueryRating值最大不超过200，因此，计算查询QueryRating值将其对应1到200个位置中相应的位置置1，其余置0。例如，查询组合 (Q1，Q2，Q3)， 则其输入特征为 (QPF1,QIF1,QPF2,QIF2,QPF3,QIF3)。 为了便于计算，本文对少于25个操作类型的查询采取补零方法补成3075位。每一个QIF含有两个QueryRating值共400位，如Q1的QIF包含(QueryRatingQ1,Q2,Query-RatingQ1,Q3)。所以3个查询并行运行，其输入神经元的个数为3*(3075+400) 等于10 425。

训练神经网络模型时，除了需要特征向量，还需要预测标签也就是模型的输出，本文采用直接预测时间的方法。一个查询组合有m个查询，那么预测标签则为与之对应的m个响应时间。

2.3 固定查询组合预测

2.3.1 问题定义

我们通过例子来说明本节要解决的问题，如图3所示，假设有3个查询1、2、3同时运行，每有查询结束则继续向系统提交该查询，保持查询组合不变。预测固定查询组合(1，2，3)中查询1、2、3各自的响应时间。

图3 固定查询组合运行示例

根据上述问题，将预测问题定义为：

定义1 问题定义：查询集合S={Qi|i=1,2,…,M}， 并行程度为M，则将查询集合S中的M个查询提交到数据库运行，运行过程中查询组合保持不变，分别预测M个查询的响应时间。

2.3.2 解决方案

本节通过全连接神经网络模型来预测固定查询组合下查询的响应时间，如图4所示。获取查询计划、查询交互结果数据(OLAP系统中抽取)，将这两部分数据按照2.2.2节编码成模型的输入特征，输入到全连接神经网络模型中进行训练，得出模型。对于待测试的查询组合，组合查询的查询计划特征、查询交互特征输入到模型，预测出查询组合中各查询的响应时间。

图4 模型框架

2.4 可变查询组合预测

2.4.1 问题定义

由第2.1节图1可知，查询5经历了(5,1,3)与(5,2,3)两个查询组合，在不同组合中资源的争用情况不同，显然在查询组合(5,1,3)时采用全连接神经网络模型给出查询5响应时间不能准确反映其真实的响应时间。对可变查询组合的预测问题就演变查询1结束时，对查询5的剩余时间估计。

根据以上描述，将预测问题定义为：

定义2 问题定义：查询集合S={Qi|i=1,2,…,N}， 并行程度为M，则从查询集合S中随机选M个查询提交到数据库运行；当某一个查询运行完成，数据库系统从剩余N-M个查询中随机选取一个与正在运行的查询组成新的查询组合并估计不包含新查询的其它查询的剩余时间。

2.4.2 解决方案

针对可变查询组合响应时间预测问题，使用全连接神经网络模型与剩余时间估计方法(式(2))共同实现对查询剩余时间的估计[11]。同时记录初始时刻、每个查询的结束时间、查询在每个线程中的执行顺序与所经历的组合数，结合算法1给出查询队列中所有查询的响应时间

(2)

式中：查询Qi包含于Com1与Com2两个组合，当查询Com1组合中有一个查询结束时，对查询Qi的剩余时间进行估计；其中，T右上标的f、i分别代表查询Qi在查询组合ComX(X=1、2) 中已运行的时间、固定查询组合中的响应时间；前两部分时间的比值代表查询Qi完成的任务量；1减去比值那部分代表查询Qi剩余的任务量；由于Qi的完成时间包含在两个查询组合中，不同组合中受到的查询交互不同，存在总任务量大于1的情况，采用tanh()函数确保剩余的任务量范围在(0，1)之间。

具体实现如下：

(1)某一查询结束，新查询到来时判断新查询组合是否在固定查询组合响应时间样本库中：如果在，取出样本库中的查询的响应时间；如果不存在，调用全连接神经网络模型给出预测；

(2)依据式(2)剩余时间估计方法，给出查询组合中未运行完成查询的剩余时间，加上查询已运行的时间预测出查询的剩余时间；

(3)判断查询队列是否结束，若没结束，循环上述两步估计查询的剩余时间，直到查询结束。

完成查询队列中查询剩余时间的估计后，结合算法1给出查询队列中每个查询的响应时间。其中，第(1)行变量初始化；第(2)行～第(10)行依次计算Nc-1个查询的响应时间；其中第(3)行～第(9)行计算m+1线程中所有查询的响应时间；第(4)行～第(6)行，获取查询所涉及到的组合数并赋值给cur，arr[cur]取出第cur个时间，arr[per] 取出开始时间，两部分差值得到查询的响应时间，同时将cur赋值给per，下一个的cur等于赋值后的per加上查询涉及到的组合数；第(7)行记录查询的响应时间；第(8)行，记录查询的个数。第(11)行返回所有查询的响应时间。

算法1： 计算查询响应时间的算法

输入：

arr[1,…,nt,…,p] //初始时刻与每个查询依次完成时刻的组合

i[1,…,nt,…,Nc][1,…,n1c,…,N1c][1,…,n2c,…,N2c]

//线程， 查询ID， 查询经历的组合数

输出：

{time}1i//time是i个查询的响应时间

Begin

(1) per←0,i←1

(2)form=0 to Nc-1do

(3)forn=0 to N1c-1do

(4) cur←per + i[m][n][1]

(5) t←arr[cur]-arr[per]

(6) per←cur

(7) time←t

(8) i++

(9)endfor

(10)endfor

(11) return {time}1i

End

3 实验分析与验证

本章3.1节介绍实验环境与数据集，3.2节介绍对模型的评估，3.3节介绍相关实验设计与实现。

3.1 实验环境与数据集

实验采用Java与Python语言共同开发，系统环境为Windows10，处理器为Inter(R) pentium(R) CPU G4400@3.30 GHz 3.31 GHz实验数据来源于TPC-H，选用PostgreSQL数据库、大小10 GB。

人工神经网络通常需要采集大量的数据进行训练，因此本文在22个查询模板的基础上增加了单表查询、多表连接、表的聚合操作查询，有助于统计更多的查询组合数据，提高模型的拟合能力。实验从25个查询模板选取并行程度为3的查询组成2300个查询组合，针对不同的实验选取不同覆盖率的训练样本进行实验。

3.2 模型评价

实验通过两方面来实现对模型的评估：均方误差(mean square error，MSE)、Acc。MSE用来对数据的变化情况进行评估，Acc用来对模型预测的准确率进行评估(并行度为3时准确率的计算公式)。具体实现如式(3)、式(4)所示

(3)

(4)

式(3)中，MSE是预测值与真实值差值平方的期望；式(4)中，Acc是对待预测查询组合中所有查询响应时间预测准确率的均值。n表示有n个查询组合，3n表示n个查询组合共有3n个查询，pi表示模型预测出的查询i的响应时间，yi为查询i在查询组合中真实运行的时间。MSE值越接近于0，预测值越逼近真实值。Acc越大说明模型预测越准确。

3.3 实验设计与分析

3.3.1 全连接神经网络模型收敛性

采用2300个查询组合数据的80%作为训练集(训练集的20%作为验证集)，训练模型，得到训练集与验证集的损失变化如图5所示。

图5 训练集与有效集的损失

图5中，横坐标表示查询组合迭代的次数，纵坐标表示损失，虚线表示训练集损失变化曲线，实线表示验证集损失变化曲线；随着迭代次数增加，模型收敛，训练集和验证集的损失变化趋势迅速减小并趋于稳定，说明预测值趋近于真实值，模型稳定。在模型趋于稳定的情况下，计算测试集的查询组合的MSE值为0.0043说明预测值接近于真实值。

3.3.2 样本覆盖率60%情况下3种模型比较

实验从2300个查询组合中选取60%的数据作训练集，模拟真实复杂数据库训练集样本覆盖率较低的情况。待预测查询组合由复杂度不同的9个查询并行程度为3组成。并行程度为3的查询组合(Qi，Qj，Qk)，采用相似性模型、仅由查询计划建立的全连接神经网络模型、本文设计的全连接神经网络模型分别对待预测查询组合中位于第一、二、三个位置的Qi、Qj、Qk进行预测，并计算这些位置的预测准确率，结果如图6所示。

图6 3种模型预测准确率比较

全连接神经网络平均预测准确率可达 (72.3%+64.5%+63.85%)/3=66.85%， 仅由查询计划建立的全连接神经网络模型平均预测准确率为 (56.2%+46.7%+58.89%)/3=53.93%， 相似性模型平均预测准确率为 (62.1%+58.2%+53.2%)/3=57.8%。 在样本覆盖率较低的情况下，本文设计的全连接神经网络模型预测准确率较相似性模型和仅由查询计划建立的全连接神经网络分别高12.92%、18.25%，说明了本文选取查询计划与查询交互共同作为输入的合理性、必要性。

3.3.3 固定查询组合预测准确性

实验对待预测查询模板为1、4、5、6、8、10、12、14、18选取并行程度为3组成84个查询组合。由表2可知相似性模型与全连接神经网络模型随着样本数量的增加，模型准确率有所提高。样本数量为2300时，相似性模型的模型准确率为86%，全连接神经网络模型准确率93.79%。

表2 模型准确率比较

全连接神经网络模型有较高的准确率是由于全连接神经网络自学习、拟合能力强且本文的全连接神经网络模型输入特征在相似性模型特征的基础上增加了查询计划，使输入特征能够更好得表征查询。

3.3.4 动态估计可变查询组合中查询的剩余时间

实验采用并行程度为3，查询模板为1、4、5、6、8、10、12、14、18的查询并行运行，如图7所示。

图7 随机选取3个查询并行执行

由图7可知，查询模板构成了7种并行程度为3的查询组合，某一查询结束时，对组合中其余查询剩余时间进行预测，其预测值与真实值见表3，其中模型剩余时间是指全连接神经网络模型与相似性模型对待预测查询剩余时间的估计。经计算，全连接神经网络模型预测准确率为79.99%，相似性模型准确率为73.75%。两种模型在可变查询情况下的准确率均低于固定查询组合是由于本文对可变查询组合研究是基于查询是匀速执行的，匀速执行的查询难以精确估计查询在已经历的查询组合中查询完成的工作量占整个查询的比例。

表3 模型剩余时间估计

4 结束语

本文以OLAP系统需要周期性运行批量固定查询为研究对象，提出采用全连接神经网络预测并行查询响应时间。全连接神经网络具有良好的自学习能力、拟合能力，且无须提前确定模型函数。除此之外，本文充分考虑了查询交互的影响，结合查询计划信息能够更为准确的预测查询组合中各查询的响应时间；实验结果表明，在10 GB数据集上，本文提出的模型可实现动态预测；且无论样本覆盖率如何，全连接神经网络模型都优于当前代表性统计模型。在后续工作中，可在本文的基础上对负载调度进行研究，根据查询响应时间调整查询的执行顺序，选取资源争用小的查询并行运行，缩短整个查询队列的执行时间，提高数据库运行效率。