基于高速均匀性数据分析的轮胎固有频率测算方法
2021-07-21李慧敏刘宝涛张凯凯王龙庆
李慧敏,刘宝涛,张凯凯,王龙庆
(青岛森麒麟轮胎股份有限公司,山东 青岛 266229)
轮胎是由多种材料经多道工序复合而成的产品,其生产过程不可避免地会存在质量、刚性和尺寸的不均匀性,这种不均匀性在轮胎高速运转过程中会产生径向力、侧向力及纵向力波动,波动幅度达到一定程度会影响汽车的振动和噪声状况[1-3]。轮胎高速均匀性试验机是一种专用于测试轮胎在高速和负荷情况下力学特性参数的检测设备,不同于低速均匀性检测,它可以更准确地模拟轮胎在高速运转过程中的力学特性,因此其检测数据更具参考性。
高速均匀性检测的是轮胎高速运转过程中径向力、纵向力和侧向力的周期性变化,是时域上复杂的周期性力的波动,通常采用傅里叶级数的方法将其分解成多个谐波的叠加。每次谐波的频率对应的是相应的轮胎滚动频率的倍数。当某一速度下的某一谐波频率接近轮胎的固有频率时,会引起胎体的共振,力的响应将发生“爆炸性”的增长。因此通过对力的强迫响应的观测,可以计算轮胎的固有频率。
本工作基于高速均匀性数据,通过对径向力的分析,测算径向一阶固有频率。
1 测算方法
使用ZF HSU-L-5.3型高速均匀性试验机(德国采埃孚集团产品)按照GMW 15120(2012)获得205/50ZR17轮胎一组高速均匀性试验数据,试验机数据处理系统自动进行傅里叶变换,输出各次谐波的幅值,见表1。
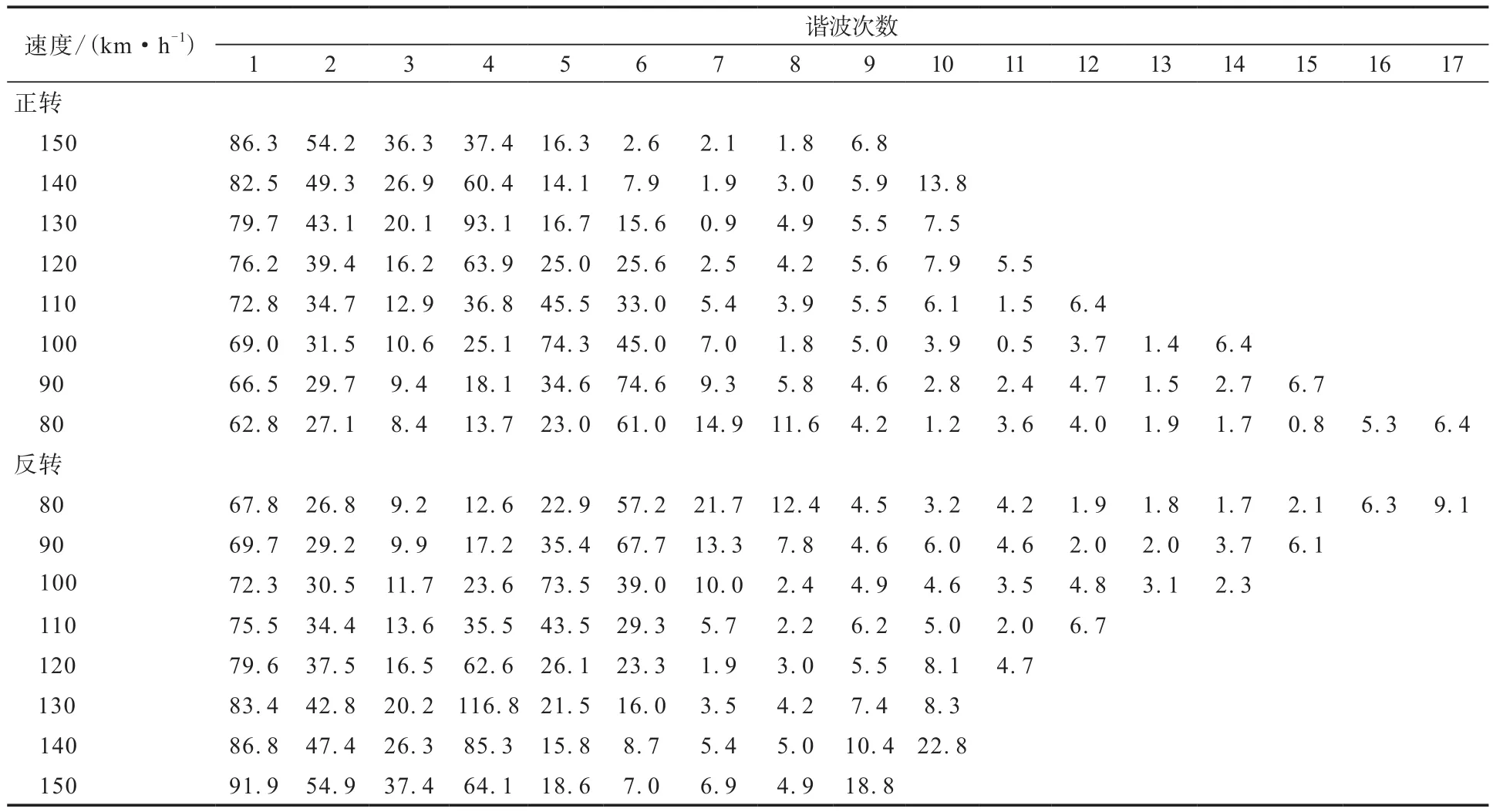
表1 205/50ZR17轮胎高速均匀性径向力各次谐波幅值 N
由表1可见,径向力各次谐波幅值整体随谐波次数增大而减小,一次谐波幅值较大,其余数据较为杂乱,不易进行分析。
使用Minitab软件对不同速度下各次谐波的幅值进行分析,查看谐波幅值与轮胎速度的相关性,径向力1—6次谐波幅值与速度的二次拟合曲线如图1—6所示。径向力1—6次谐波幅值与速度的二次拟合曲线方程分别如下:

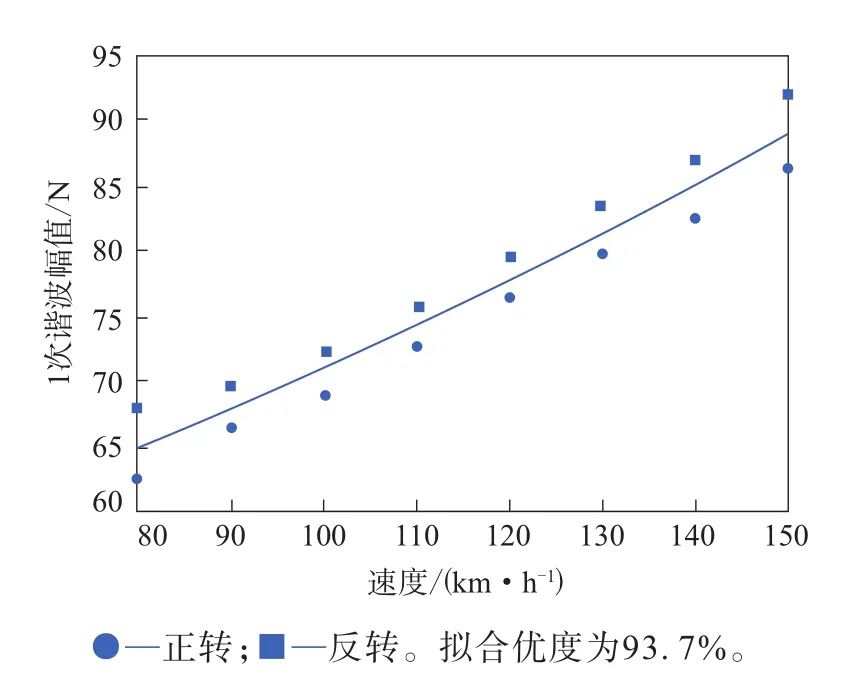
图1 径向力1次谐波幅值与速度的二次拟合曲线
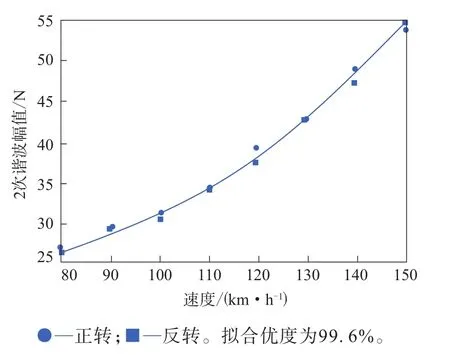
图2 径向力2次谐波幅值与速度的二次拟合曲线
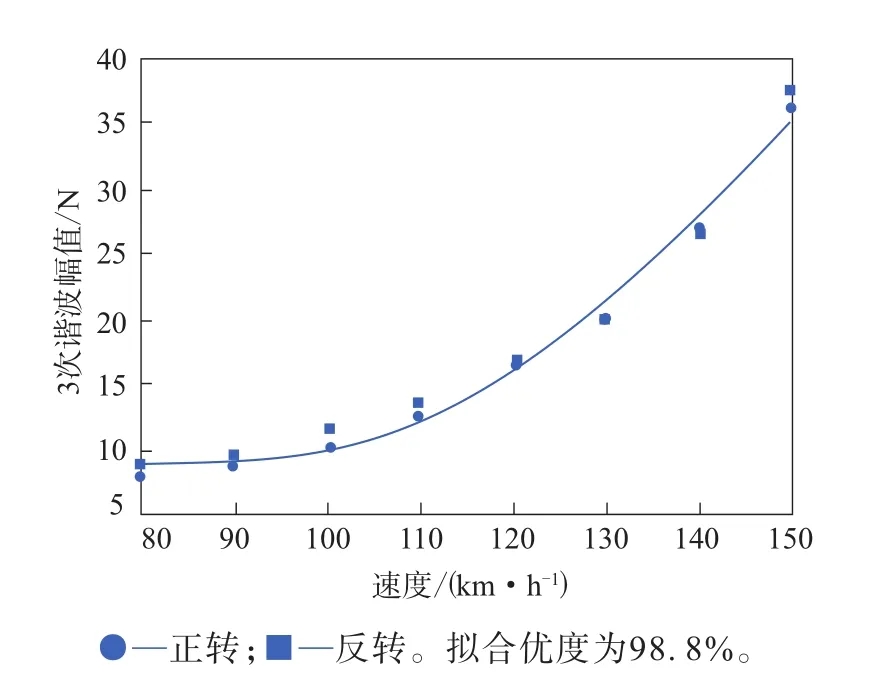
图3 径向力3次谐波幅值与速度的二次拟合曲线
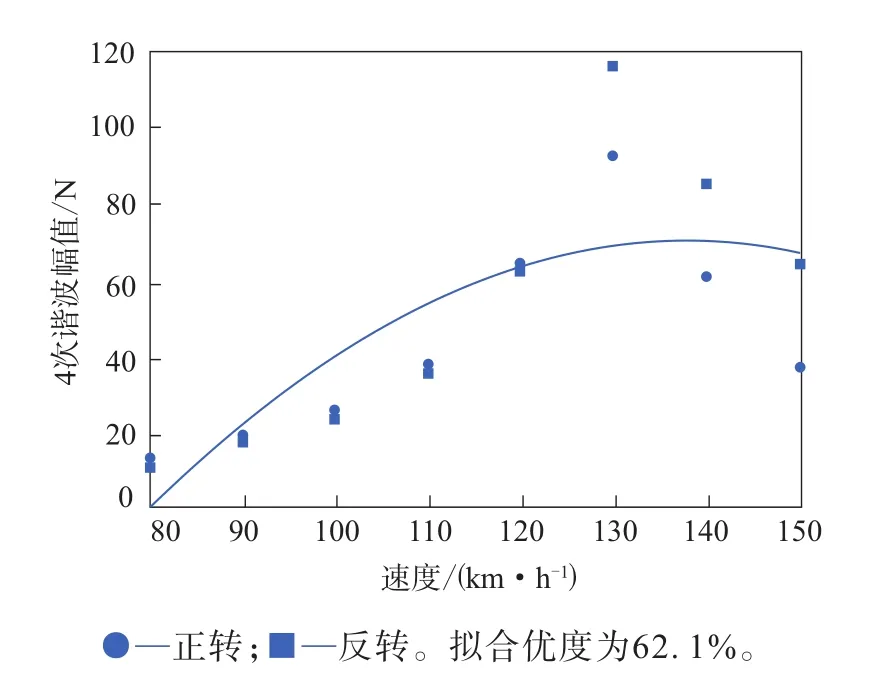
图4 径向力4次谐波幅值与速度的二次拟合曲线
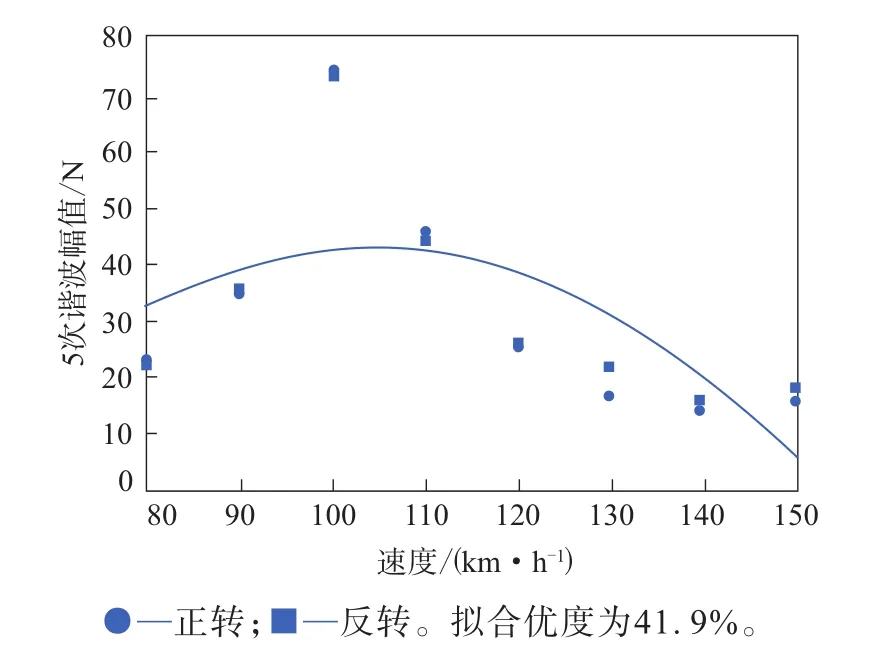
图5 径向力5次谐波幅值与速度的二次拟合曲线
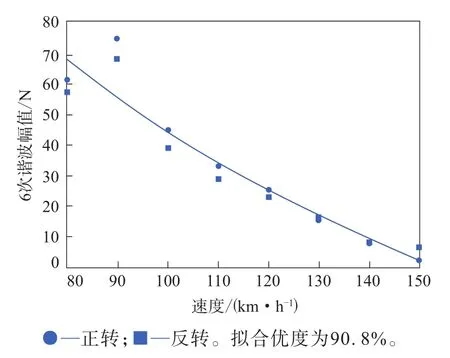
图6 径向力6次谐波幅值与速度的二次拟合曲线
由图1—6可以看出:径向力的前3次谐波幅值与速度的二次拟合曲线的拟合优度均在90%以上,呈现出很强的速度依赖性;径向力的4—6次谐波幅值大部分仍落在与速度的拟合曲线上,但有个别速度对应的谐波幅值出现了突变,且随着谐波次数的增大,出现突变的数据对应的速度减小。
对以上数据突变的谐波幅值进行频率(f)计算:

式中,r为轮胎转速,n为谐波次数,v为轮胎速度,l为轮胎滚动周长。
计算得各谐波幅值突变数据对应的频率见表2。
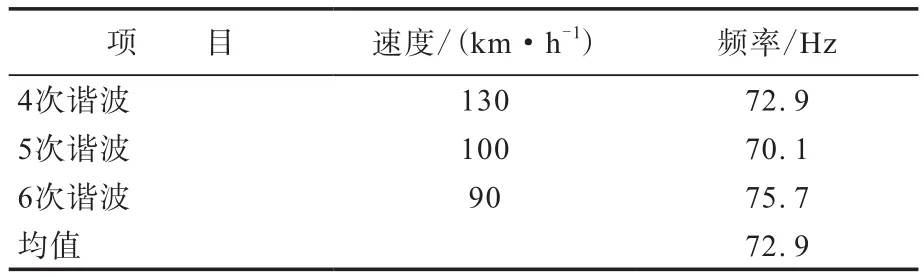
表2 谐波幅值突变数据对应的频率计算结果
由表2可以看出,谐波幅值突变数据对应的频率趋于一致,均值为72.9 Hz,即径向力的4次、5次、6次谐波分别在130,100,90 km·h-1速度下的频率处激起共振,导致力传感器感应到的力大幅增大,由于轮胎的径向一阶固有频率一般分布在60~100 Hz内,频率越低,能量越高,越容易被激起振动,因此测算得到的频率均值为轮胎径向一阶固有频率,同时可以粗略地认为,被激起的平均幅值为轮胎一阶径向模态的力的响应幅值。
2 正确性验证
2.1 理论验证
对于无阻尼自由系统,其固有频率(f0)计算公式如下:
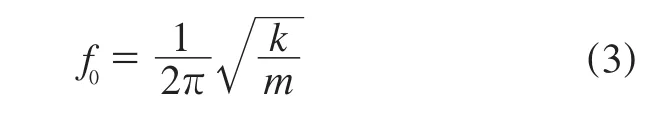
式中,k为径向刚度,N·m-1;m为质量,kg。
由式(3)可以看出:不考虑阻尼,结构的固有频率只受径向刚度和质量的影响,质量增大,结构的固有频率减小;径向刚度增大,结构的固有频率增大。
不同于无阻尼自由系统,轮胎具有复杂的结构和多个自由度,并有阻尼,但结构的固有频率的主要影响因素仍是径向刚度和质量,且作用方向一致,阻尼对固有频率的影响非常有限[4-5]。
选取某配套项目试制的6个方案试验轮胎及标准轮胎分别进行高速均匀性试验,按上述方法获取轮胎径向一阶固有频率及径向力幅值,结果见表3。

表3 试制方案及标准轮胎的径向一阶固有频率计算值
对f1与的回归拟合可以得到如下方程:
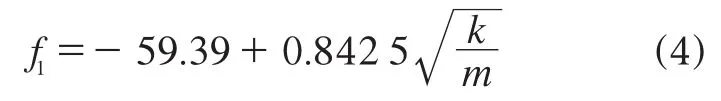
调整后的拟合优度高达84.3%,因此认为此数据模型有效,即质量增大,结构的固有频率减小;径向刚度增大,结构的固有频率增大,与理论相符。
对A与k回归拟合可得如下方程:
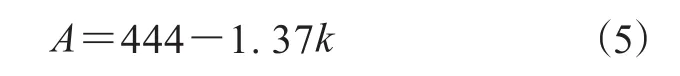
调整后的拟合优度为75.7%,因此认为模型有效,径向刚度增大,低频段输出力的幅值减小,与理论相符。
2.2 力传感函数试验验证
对方案A和E轮胎同时进行力传感函数试验,获取径向一阶固有频率。根据GMW 14876(2014)法规进行参数设定,试验采用SCADAS SCM2E05(32 CHs)(日本西门子公司产品)数据采集设备,Test Lab 18A型分析系统,PCB Hammer 086C03型激励传感器,PCB Tri-axis 356A32型加速度传感器。
力传感函数试验结果如图7所示,两种方法测算的径向一阶固有频率对比见表4。
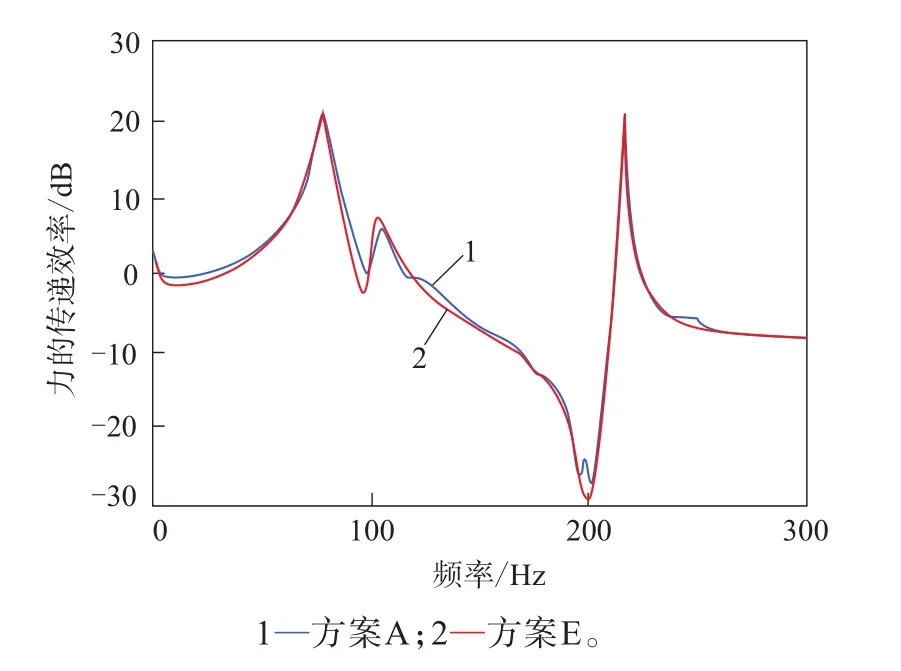
图7 力传感函数试验结果

表4 两种方法测算的径向一阶固有频率对比 Hz
由图7和表4可见,通过两种方法获取的径向一阶固有频率基本一致,相差约1 Hz,这可能是因为力传感函数测量的是静态轮胎的径向一阶固有频率,而通过高速均匀性数据测算的是工作状态下的径向一阶固有频率,由于轮胎生热,胎体帘线模量减小,轮胎整体刚度减小,导致固有频率减小。
通过固有频率影响因素和力传感函数测算的验证,确认通过高速均匀性数据测算f1的方法是可行的。可以通过减小高速均匀性试验的速度梯度来提升测算的精确度,无特殊要求时高速均匀性试验一般采用10 km·h-1的速度梯度,若用于测算径向一阶固有频率,可以针对某一较小的速度段将速度梯度调整为2 km·h-1。
3 结构设计对固有频率的影响
对215/50R17轮胎不同结构设计方案(见表5)进行分析。
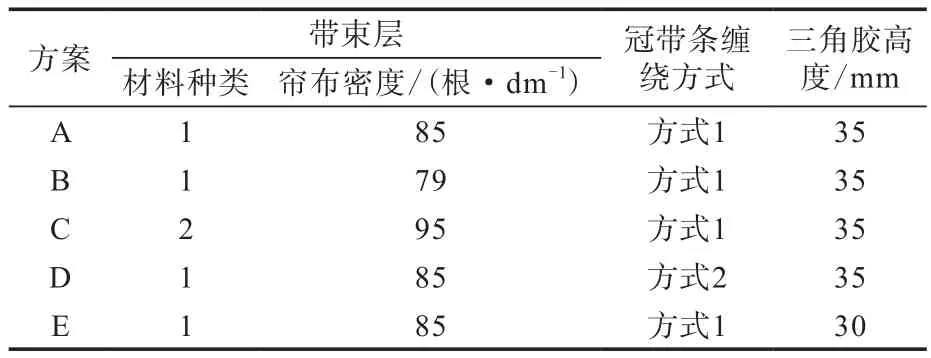
表5 结构设计方案
结合表3和表5可以看出以下几点。
(1)对比方案A与B,带束层帘布密度减小,轮胎的径向刚度降低,质量减小,径向一阶固有频率降低,因此调整带束层帘布密度,径向刚度对固有频率的影响大于质量。
(2)对比方案A与C,带束层帘线种类和帘布密度均发生变化,径向刚度和质量均减小,径向一阶固有频率不变,说明带束层设计的变化对固有频率的影响不大。
(3)对比方案A与D,冠带条缠绕方式调整,径向刚度降低,质量减小,径向一阶固有频率增大,因此调整冠带条缠绕方式,质量对固有频率的影响大于径向刚度。
(4)对比方案A与E,三角胶高度减小5 mm,径向刚度降低,质量减小,径向一阶固有频率降低,因此调整三角胶高度,径向刚度对固有频率的影响大于质量。
4 结论
(1)通过Minitab软件对高速均匀性数据中各次谐波幅值进行分析,对于发生突变的数据通过其对应的谐波次数和速度计算频率,多个数据对应的频率比较接近,其均值可以认为是径向一阶固有频率,被激起的谐波幅值均值可以认为是共振点的幅值。
(2)可通过减小高速均匀性试验的速度梯度来提升轮胎固有频率的测算精确度。
(3)通过高速均匀性测算的固有频率比通过力传感函数测得的固有频率略小,这可能是因为工作状态下生热导致轮胎整体刚度减小,固有频率相应减小。
(4)结构设计对轮胎固有频率有影响,冠带条缠绕方式影响较大,带束层设计对一阶径向固有频率的影响不大。
本方法测算的是轮胎在一定充气压力和负荷下运转时的固有频率,更贴合轮胎的实际工作状态,若合理运用可以在不进行力传感函数测试的情况下,在测试轮胎高速均匀性数据的同时获取轮胎的低阶固有频率及幅值,可指导轮胎的结构优化,缩短测试周期,具有很好的实用性。
