交流供电制式下矿山法地铁隧道的牵引回流分布特征分析

李鲲鹏 靳守杰 李俊豪 曹晓斌 朱传林

(1.西南交通大学电气工程学院， 611756， 成都； 2.广州地铁设计研究院股份有限公司， 510010， 广州；3.广州地铁集团有限公司， 510330， 广州∥第一作者， 正高级工程师)

与直流供电制式相比，采用25 kV交流供电制式的线路，因接触网供电区间长度较长，列车的运行速度较快[1]。因此，我国在几个主要的大城市规划了25 kV交流供电制式的城市轨道交通线路。

直流供电制式下地铁的杂散电流是回流系统的1个重要问题[2-3]。采用交流供电制式后，杂散电流的问题可能比直流供电制式更加严重，其主要原因为：三相交流变压器的一相与牵引变电所接地网及钢轨相连，另外两相连接不同区间的接触网。列车从接触网上取得牵引电流，再通过车轮传给钢轨。由于钢轨与大地无法做到绝对绝缘，因此牵引电流通过由钢轨、回流线和大地组成的回流系统回到变电所。此外，交流牵引电流不仅可以通过钢轨对地的泄漏电阻流入大地，还可通过空间电磁耦合在隧道与桥梁等钢筋结构中产生感应电流。这些电流流入大地后成为杂散电流，危害周边人身与设备安全。

大量学者已经对传统直流制供电地铁牵引回流分布进行了研究[4-6]，而交流制下的地铁隧道回流属新生事物，尚未见相关的研究报告。本文根据设计的需求，对比分析了交流供电与直流供电2种制式下泄漏电流的分布规律，重点研究了交流供电下矿山法地铁隧道结构中泄漏电流的分布规律及影响因素，为设计人员提供参考。

1 建立地铁隧道模型

1.1 设定走行轨的等效参数

城市轨道交通线路大多采用60 kg/m型钢轨，其断面面积为77.45 cm2，等效的圆柱体截面半径为0.05 m。走行轨纵向电阻为0.04 Ω/km[7]。

轨道对地之间存着一定的过渡电阻。本文采用CDEGS软件建模，通过添加固定电阻率的绝缘涂层实现对过渡电阻的控制。涂层电阻率的计算公式为：

(1)

式中：

ρ——绝缘层电阻率，Ω·m；

Rg——轨地过渡电阻，Ω；

r1——裸导体半径，m；

r2——含绝缘层的导体总半径，m。

CJJ/T 49—1992《地铁杂散电流腐蚀防护技术规程》规定：兼用作回流的地铁走行轨与隧道主体结构(或大地)之间的过渡电阻值不应小于15 Ω·km。(编者注：该标准现已修订为CJJ/T49—2020《地铁杂散电流腐蚀防护技术标准》。)

Rg取15 000 Ω·m、r1取0.05 m时，设涂层的厚度为0.01 m，则r2取0.06 m。根据式(1)可计算得到涂层的电阻率ρ为500 000 Ω·m。

1.2 建立牵引电流与牵引供电区间的等效模型

交流供电制式下牵引供电区间长度在15 km左右，因此本文在仿真中以15 km作为1个牵引供电区间，且设定列车位于区间未端、牵引变电所位于区间首端，牵引电流为2 000 A。

根据上文的计算结果，得到单根钢轨的仿真等效模型如图1所示，其内部为1根半径为0.05 m的实心圆柱形钢铁，长为15 km；外覆厚度为0.01 m、电阻率为500 000 Ω·m的涂层。轨道的埋深取20 m。

1.3 建立隧道的等效模型

由于隧道内部充满空气，由于CDEGS软件的MALZ模块无法设置过于复杂的土壤结构，因此仿真中用长度为15.1 km、横截面为6 m×6 m的长方体代替。空气的电阻率取1×1018Ω·m。

1.4 建立隧道的结构模型

地铁隧道的施工方法有矿山法、盾构法、明挖法和沉管法等，其中：埋深较大时多采用矿山法和盾构法，埋深较小时多用明挖法、盾构法和沉管法等方法[8]。杂散电流外溢时主要流经隧道壁的混凝土层和隧道外的土壤层。本文将土壤层的电阻率设为200 Ω·m，混凝土的电阻率取800 Ω·m。地铁隧道的整体结构示意图如图2所示。

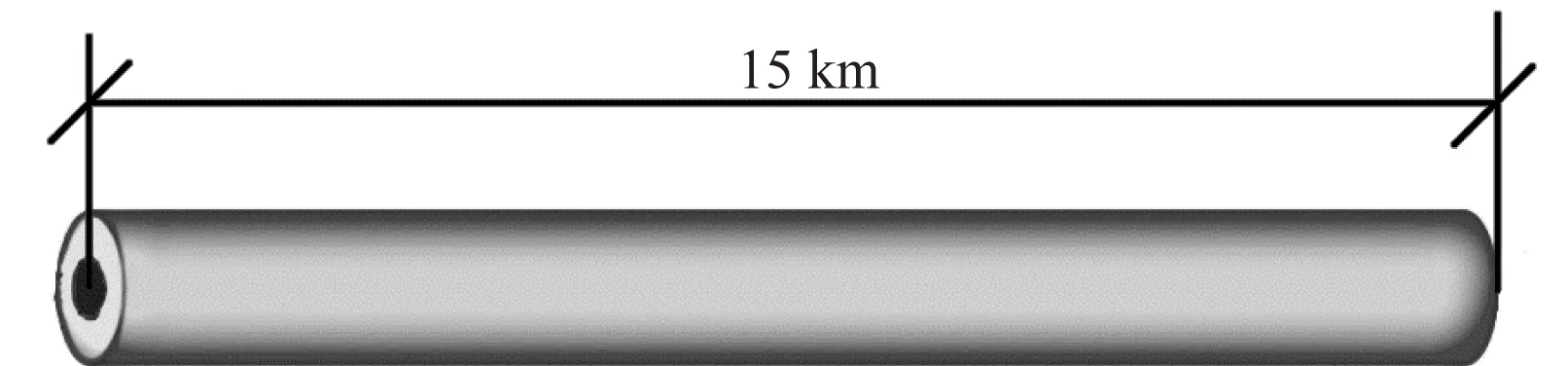
a) 单根钢轨仿真模型

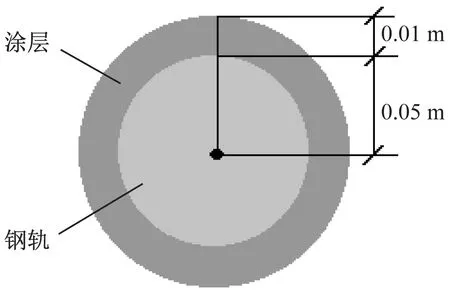
b) 单根钢轨模型截面图

a) 隧道整体结构模型

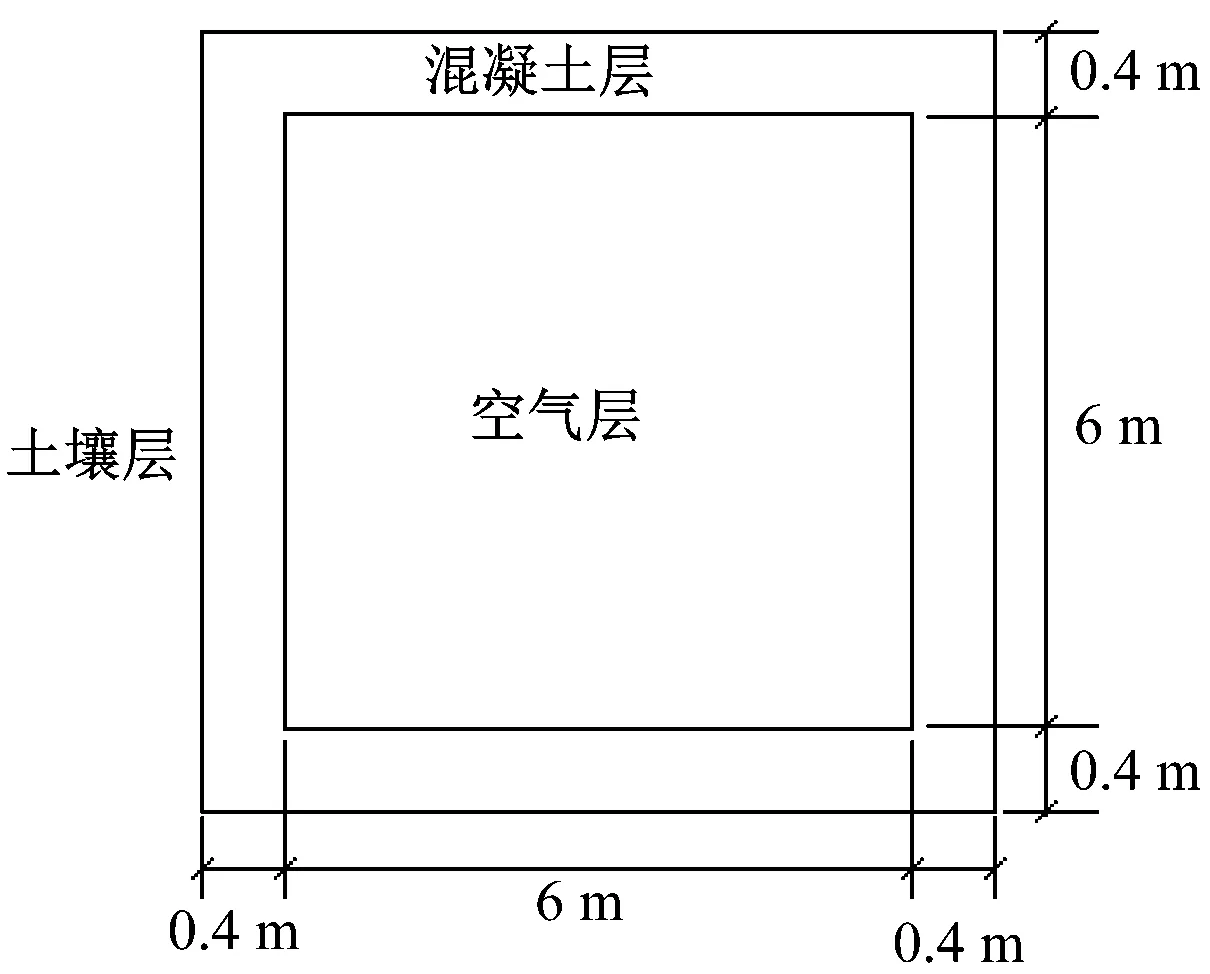
b) 隧道截面尺寸

2 不同供电制式下地铁牵引回流分布特征

交流供电制式地铁线路采用的是直接供电加回流线的供电方式，每隔1段距离采用吸上线将回流线与钢轨相连。为比较直流与交流2种供电制式的区别，仿真时在机车位置分别往钢轨中注入交流2 000 A和直流2 000 A的电流，其电流分布如图3所示，横坐标的0点处为该供电区间的中心点。

根据钢轨电流和回流线电流分布规律的仿真结果，当总牵引电流为2 000 A时，得到直流与交流2种供电制式下不同位置处的泄漏电流如表1所示。

图3 交流与直流制式下钢轨电流分布情况对比

表1 不同的距机车位置下不同供电制式电流大小对比

由表1计算可知：交流制式下流过回流线的电流占总牵引电流的22.0%～28.1%，直流制式下流过回流线的电流占总牵引电流的17.0%～18.0%，因而交流制供电下的回流线回流能力大于直流制供电下回流线的回流能力。在供电区间的中点(距机车位置7.5 km)处，交流制式下的泄漏电流值约为直流制式下泄漏电流值的4.3倍。造成泄漏电流差异如此大的主要原因是：交流供电制式下牵引电流可以通过空间电磁耦合传入周边隧道的结构钢筋中，并通过结构钢筋流入大地，从而导致泄漏电流的途径增加，泄漏电流增大。

3 交流供电制式下牵引回流分布因素

3.1 牵引供电区间长度对牵引回流分布的影响

交流制供电下地铁车站的站间距一般要比直流制供电下的站间距大，其范围为2 km至20 km不等。本文研究时先保持其他参数不变，仅改变供电区间距离，利用CDEGS软件仿真计算得到不同牵引供电区间长度下的回流电流分布情况，如图4～5所示。为了便于分析，将不同长度下的供电区间中点与图4～5中横坐标的0点对齐。

图4 不同牵引供电区间长度下的钢轨电流分布

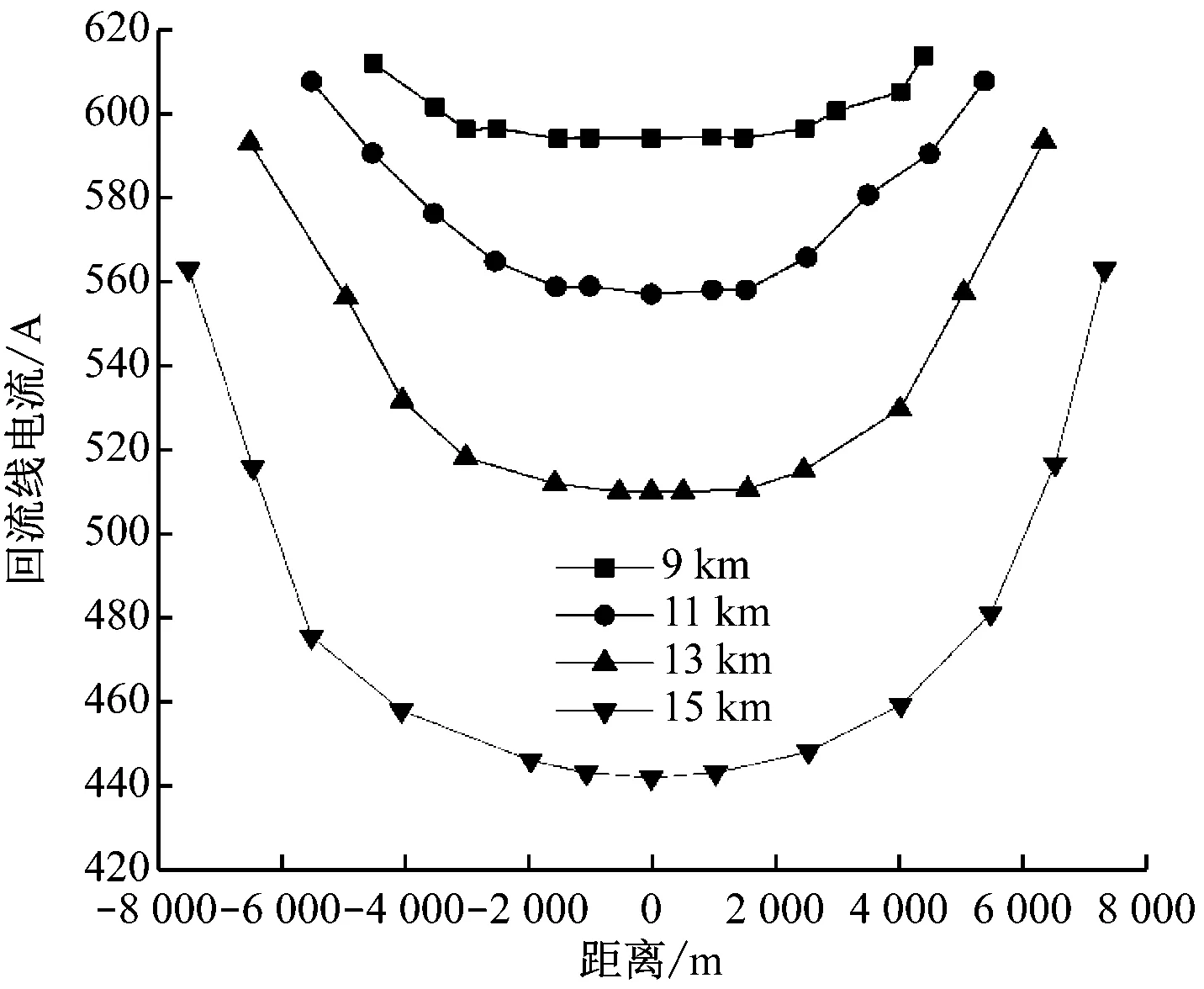
图5 不同牵引供电区间长度下的回流线电流分布

从图4～5可以发现，图中各条线都呈U型，即中点处的电流小于两端的电流。将总牵引电流减去2根钢轨的电流和1条回流线的电流后，可得到不同供电区间长度下对应的泄漏电流值，其分布规律如图6所示。

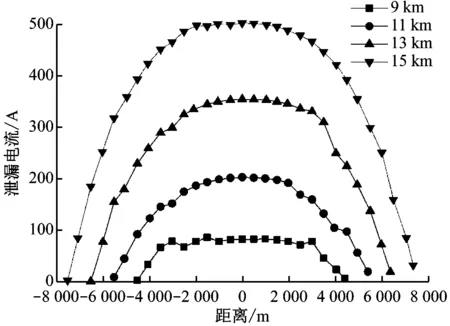
图6 不同牵引供电区间长度下的泄漏电流分布

由图4～6可知，即使牵引供电区间的长度发生变化，泄漏电流的最大值依然出现在供电区间的中点处，此处的钢轨电流值和回流线电流值最小。表2给出了不同牵引供电区间长度下供电区间中点的电流分配情况。

基于表2的数据，通过计算可以得到：牵引供电区间长度为15 km时，其中点处的泄漏电流为505 A，占总牵引电流的25.2%；牵引供电区间长度为9 km时，其中点处的泄漏电流为84 A，仅占总牵引电流的4.2%。因而可以得出结论，大地的泄漏电流大小与牵引供电区间的长度密切相关。

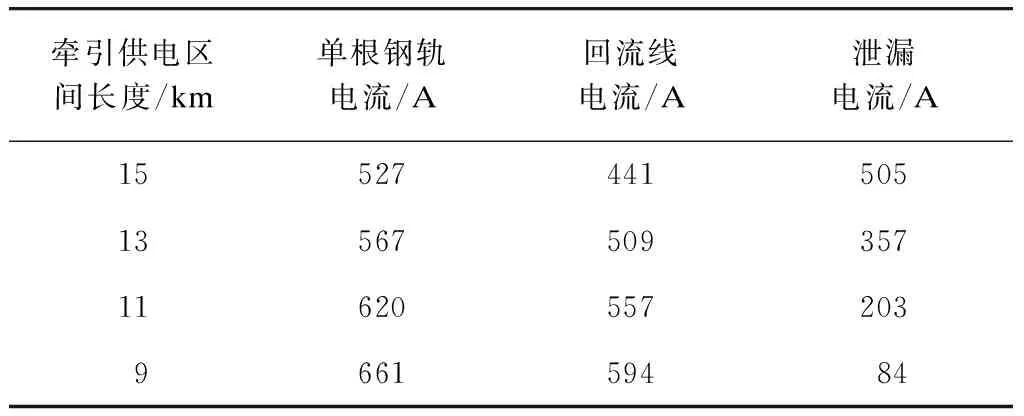
表2 不同牵引供电区间长度下供电区间中点的电流分配

3.2 土壤电阻率对回流电流分布的影响

本文以广州某地铁线路为例进行研究。该线路的实测土壤电阻率区域范围为15～600 Ω·m，故在模型中分别设置了土壤电阻率的5个等级：15 Ω·m、150 Ω·m、200 Ω·m、400 Ω·m、600 Ω·m，用以研究土壤电阻率对回流分布的影响。仿真得到的钢轨电流分布及泄漏电流分布分别如图7～8所示。

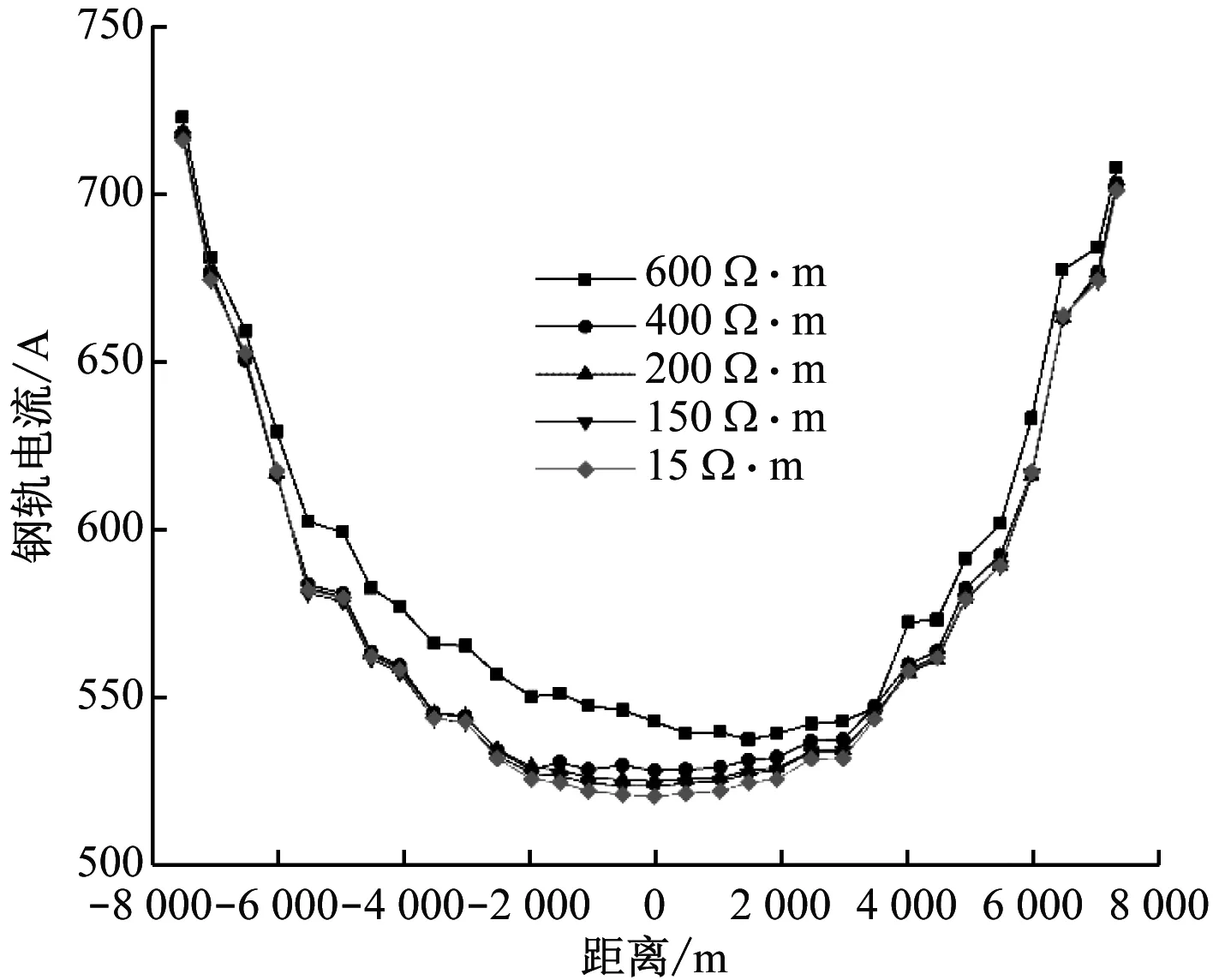
图7 不同土壤电阻率下的钢轨电流分布

从图7～8可以看出，随着土壤电阻率增大，供电区间中点处流过的钢轨电流增大，泄漏电流减少。当土壤电阻率为15 Ω·m时，供电区间中点处的泄漏电流为519 A；当土壤电阻率增至600 Ω·m时，供电区间中点处的泄漏电流减少到471 A，但其变化量仅占总牵引电流的2.4%。

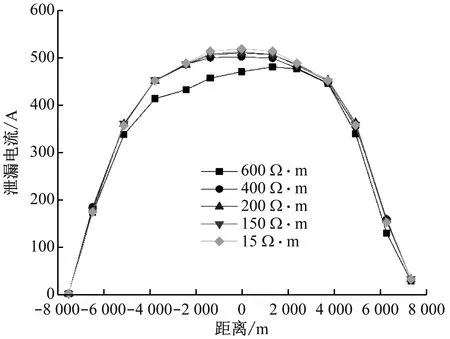
图8 不同土壤电阻率下的泄漏电流分布

通过上述分析可知，牵引供电区间的长度才是影响交流供电制式下泄漏电流的主要因素，土壤电阻率对牵引回流系统的影响并不大。因此，减少牵引供电系统对地泄漏电流的主要途径是减少牵引供电系统与周边结构钢筋的电磁耦合系数，设计中可通过减少供电区间长度或将隧道结构钢筋进行绝缘分段实现。

4 结论

1) 交流供电制式下的泄漏电流不仅可以通过钢轨对地泄漏电阻产生，还可以通过空间电磁耦合传入周边隧道等设施的结构钢轨中，这导致了交流供电制式的泄漏电流大于直流供电制式的泄漏电流。如在15 km的牵引供电区间内，交流供电制式下的泄漏电流可达400 A，为同等条件下直流供电制式下泄漏电流的5倍左右。

2) 交流供电制式下的牵引供电区间长度越长，泄漏电流越大，且最大泄漏电流与区间长度呈非线性关系。当供电区间长度为9 km时，其最大泄漏电流小于100 A；当供电区间长度增大至15 km时，其最大泄漏电流大于500 A。

3) 土壤电阻率对泄漏电流有一定的影响，但不是泄漏电流的主要影响因素。

4) 交流供电制式下泄漏电流主要通过空间电磁耦合产生，因此对采用交流供电制式的城市轨道线路进行设计时，可以通过减少供电区间长度或将隧道结构钢筋进行绝缘分段的方式来减少电磁耦合，以降低泄漏电流。