基于优化ORB算法的图像角点特征匹配方法*

朱 标

(1.中航华东光电有限公司，安徽 芜湖 241002； 2.安徽省现代显示技术重点实验室，安徽 芜湖 241002；3.国家特种显示工程技术研究中心，安徽 芜湖 241002； 4.特种显示国家工程实验室，安徽 芜湖 241002)

0 引 言

图像角点特征匹配作为计算机视觉领域的重点研究方向之一，其普遍应用于机器人[1]、无人机[2]与SLAM(Simultaneous Localization and Mapping)[3]等领域。首先，调研了国外科研者提出的图像角点特征匹配算法，例如， SUSAN(Smallest Univalue Segment Assimilating Nucleus)算法[4]、Trajkovic算法[5]和FAST (Features from Accelerated Segment Test)算法[6-7]， SIFT(Scale Invariant Feature Transform)算法[8-9]、SURF(Speeded up Robust Feature)算法[10]、ORB(Oriented FAST and Rotated BRIEF)算法[11]等，其中，SUSAN算法、Trajkovic算法与FAST算法作为依次优化的经典图像角点特征检测算法，其具备检测位置准确、抗噪声能力强的特性，但不具备对光照、尺度和旋转不变性，SIFT算法与SURF算法具备光照、尺度和旋转不变性，但执行速度不高，ORB算法具备执行速度快的特性，但存在配准精度不高的问题。重点针对Ethan Rublee等于2011年提出的ORB算法进行研究，发现该算法对目标平移、旋转与一定视角和光照等变化保持一定的不变性，但存在对尺度变换敏感和图像角点特征匹配精度不高的问题，国内科研者为了解决ORB算法存在的问题提出了许多优化算法，例如，白雪冰等[12]利用Hessian矩阵检测角点特征，使得检测出的角点特征具有尺度不变性，然后使用ORB算法生成角点特征描述子向量，解决了ORB算法对尺度变换敏感问题；曾庆化等[13]将ORB算法融入ASIFT(Affine-SIFT)算法中，加快ASIFT算法的运行速度；马丹等[14]使用SURF算法检测出具有尺度不变性的特征点，然后使用ORB算法对特征点进行描述，从而使改进ORB算法具备尺度不变性；江泽涛等[15]将ORB算法应用到异源图像的匹配，为异源图像的匹配提供了一种解决途径；杨炳坤等[16]使用Shi-Tomasi算法剔除大部分的伪角点特征，将Shi-Tomasi算法和ORB算法相结合提升了角点特征匹配精度[17]；通过对国内的调研可知，传统ORB算法普遍存在尺度变换敏感和图像角点特征匹配精度不高的问题，国内科研工作者主要利用其他图像角点特征检测和匹配算法的优势来对传统ORB算法进行优化，以解决传统ORB算法的劣势。最后，针对传统ORB算法图像角点特征匹配精度不高的问题，使用Shi-Tomasi算法、BRIEF(Binary Robust Independent Element Feature)[18]和SURF相融合算法、随机投影原理与优化的相似性距离算法对传统ORB算法进行优化，得到Shi-Tomasi- SURFORB算法。

1 Shi-Tomasi-SURFORB算法

Shi-Tomasi-SURFORB算法按照实现流程分成3个阶段：检测阶段，包括待匹配图像的采集和使用Shi-Tomasi算法检测角点特征两个阶段；描述子阶段，包括两个阶段，一是生成128维BRIEF描述子向量和64维SURF描述子向量，共192维角点特征描述子向量，二是使用随机投影原理将64维SURF描述子向量降维到24维SURF描述子向量，最终得到共152维角点特征描述子向量；匹配阶段，使用优化的匹配算法进行角点特征的匹配。Shi-Tomasi-SURFORB算法的实现流程框图如图1所示。

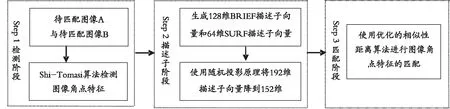
图1 Shi-Tomasi-SURFORB算法的实现流程框图Fig.1 Implementation process diagram of Shi-Tomasi-SURFORB algorithm

1.1 图像角点特征的检测

Shi-Tomasi-SURFORB算法在检测阶段使用Shi-Tomasi算法检测角点特征，Shi-Tomasi算法是Shi和Tomasi于1994年提出的一种图像角点特征检测算法，是Harris 算法的改进算法，该算法不易受图像旋转、光照条件、角度变化和噪声的影响，也可避免图像角点特征聚类。

Shi-Tomasi算法实现原理如下：首先，假定待检测像素点为P，计算其在X方向和Y方向的梯度；其次，计算利用X方向和Y方向的梯度计算像素点P的自相关矩阵M；再次，计算像素点P的响应量，响应量是自相关矩阵M的两个特征值的最小值，如果响应量高于选定的阈值，则像素点P是候选角点特征；最后，遍历图像并进行局部非极大值抑制，剔除局部区域内重复的角点特征，得到最终的角点特征集。

1.2 图像角点特征的双描述子序列

Shi-Tomasi-SURFORB算法在描述子阶段首先使用BRIEF和SURF相融合算法生成128维BRIEF描述子向量和64维SURF描述子向量，然后使用随机投影原理将64维SURF描述子向量降维到24维SURF描述子向量。

首先，计算角点特征的S×S大小的图像邻域P的准则τ(P；x，y)，计算表达式如下：

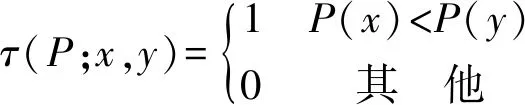
(1)

其中，τ(P；x，y)表示图像邻域P的准则，P(x)表示平滑后的图像邻域P在x处的像素灰度值，P(y)表示平滑后的图像邻域P在y处的像素灰度值，设定S的值为8。

再计算BRIEF描述子向量，BRIEF描述子向量为n维的二进制比特串，计算表达式如下：

(2)

其中，fn(P)表示n维的二进制比特串，τ(P；x，y)表示图像邻域P的准则，设定n的值为128。

其次，建立以角点特征为中心、沿角点特征主方向生成一个20×20的矩形区域，将其分成4×4个子块，对每个子块利用Haar小波模板进行响应值计算，最终形成64维SURF描述子向量。

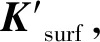
(3)

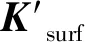
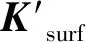
(4)

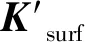
1.3 图像角点特征的匹配

Shi-Tomasi-SURFORB算法在匹配阶段使用Ham距离和欧式距离相融合的相似性距离算法进行匹配，整个图像角点特征的匹配分为两个阶段，先假定图像A与图像B为一对待匹配图像，图像A中图像角点特征集为Ubrief_i(x1，x2，x3，…，x126，x127，x128)与Usurf_i(x1，x2，x3，…，x22，x23，x24)，图像B中图像角点特征集为Vbrief_j(y1，y2，y3，…，y126，y127，y128)与Vsurf_j(y1，y2，y3，…，y22，y23，y24)。

首先，针对128维BRIEF描述子向量，使用Ham距离算法进行相似性度量，以角点特征集Ubrief_i中角点特征Ui为对象，使用Ham距离公式遍历角点特征集Vbrief_j中角点特征，得到Ham的最小值与次最小值，Ham的最小值对应最近邻特征点V1j，Ham的次最小值对应次最近邻特征点V2j，Ham距离算法如式(5)所示：

(5)

其中，xm表示Ubrief_i中角点特征描述子向量中元素，ym表示Vbrief_j中角点特征描述子向量中元素，⊕表示异或运算，Ham()表示两个角点特征描述子向量之间的Ham距离值。

如果Ham()的最小值与次最小值满足Ham距离比较定义式，则角点特征集Ubrief_i中角点特征Ui与角点特征集Vbrief_j中角点特征V1j和V2j相匹配，遍历图像角点特征集Ubrief_i中所有角点特征，得到匹配角点特征集M和N，其中M为角点特征集Ubrief_i中角点特征Ui与角点特征集Vbrief_j中角点特征V1j的组合集，N为角点特征集Ubrief_i中角点特征Ui与角点特征集Vbrief_j中角点特征V2j的组合集，Ham距离比较定义式如下：

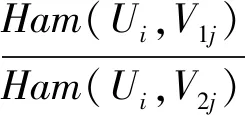
(6)

其中，Ham(Ui，V1j)、Ham(Ui，V2j)分别表示角点特征集Ubrief_i中角点特征Ui与角点特征集Vbrief_j中最近邻角点特征V1j、次最近邻角点特征V2j的Ham距离值，Th1表示设定的阈值，设定Th1的值为0.75。

然后，针对24维SURF描述子向量，使用欧式距离算法进行相似性度量，以匹配角点特征集M和N为对象，使用欧式距离算法遍历计算匹配角点特征集M和N中每对角点特征的欧式距离，得到d的最小值与次最小值，欧式距离算法如下：

(7)

其中,xm表示Usurf_i中角点特征描述子向量中元素，ym表示Vsurf_j中角点特征描述子向量中元素，d(Ui，Vj)表示角点特征之间的欧式距离值。

欧式距离的最小值和次最小值满足欧氏距离比较定义式组成的匹配图像特征集为最终匹配角点特征集F，欧氏距离比较定义式如下：

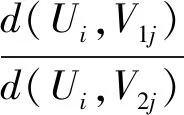
(8)

其中，d(Ui，V1j)、d(Ui，V2j)分别表示角点特征集Usurf_i中的角点特征Ui与角点特征集Vsurf_j中的最近邻角点特征V1j、次最近邻角点特征V2j的欧式距离值，Th2表示设定的阈值，设定Th2的值为0.75。

2 仿真实验

实验仿真软件为Visual Studio 2008，配置OpenCV2.4.4图像处理库，实验仿真硬件为计算机，计算机的中央处理器配置是AMD A10-7300 Radeon R6 10 Compute Cores 4 CPU+6 GPU@1.90 GHz、内存配置是4096MB RAM、操作系统配置是Windows 7 旗舰版32位。

仿真实验采用Mikolajczyk图像库中boat、bikes、graf、leuven图像作为仿真实验图像，如图2—图5所示，其中图2是发生旋转和缩放变化的boat图像，大小为850×680像素，图3是发生高斯模糊的bikes图像，大小为1 000×700像素，图4是发生视角变换的graf图像，大小为800×640像素，图5是发生光照变化的leuven图像，大小为900×600像素。

(a) boat_A (b) boat_B (c) boat_C (d) boat_D (e) boat_E (f) boat_F

(a) bikes_A (b) bikes_B (c) bikes_C (d) bikes_D (e) bikes_E (f) bikes_F

(a) graf_A (b) graf_B (c) graf_C (d) graf_D (e) graf_E (f) graf_F

(a) leuven_A (b) leuven_B (c) leuven_C (d) leuven_D (e) leuven_E (f) leuven_F

仿真实验使用传统ORB算法和Shi-Tomasi- SURFORB算法对仿真实验的待匹配图像进行角点特征检测与匹配，首先，对图2(a)与图2(b)、图2(b)与图2(c)、图2(c)与图2(d)、图2(d)与图2(e)、图2(e)与图2(f)共5对图像进行角点特征检测与匹配，其次，对图3(a)与图3(b)、图3(b)与图3(c)、图3(c)与图3(d)、图3(d)与图3(e)、图3(e)与图3(f)共5对图像进行角点特征检测与匹配，再次，对图4(a)与图4(b)、图4(b)与图4(c)、图4(c)与图4(d)、图4(d)与图4(e)、图4(e)与图4(f)共5对图像进行角点特征检测与匹配，最后，对图5(a)与图5(b)、图5(b)与图5(c)、图5(c)与图5(d)、图5(d)与图5(e)、图5(e)与图5(f)共5对图像进行角点特征检测与匹配，得到的图像角点特征检测结果图如图6—图13所示，图像角点特征匹配结果图如图14—图21所示。

(a) boat_A (b) boat_ B (c) boat_C (d) boat_D (e) boat_E (f) boat_F

(a) bikes_A (b) bikes_B (c) bikes_C (d) bikes_D (e) bikes_E (f) bikes_F

(a) graf_A (b) graf_B (c) graf_C (d) graf_D (e) graf_E (f) graf_F

(a) leuven_A (b) leuven_B (c) leuven_C (d) leuven_D (e) leuven_E (f) leuven_F

使用传统ORB算法对仿真实验的待匹配图像进行角点特征检测，角点特征检测结果图如图6—图9所示，其中图6表示对图2中boat图像的角点特征检测结果图，图7表示对图3中bikes图像的角点特征检测结果图，图8表示对图4中graf图像的角点特征检测结果图，图9表示对图5中leuven图像的角点特征检测结果图。

(a) boat_A (b) boat_ B (c) boat_C (d) boat_D (e) boat_E (f) boat_F

(a) bikes_A (b) bikes_B (c) bikes_C (d) bikes_D (e) bikes_E (f) bikes_F

(a) graf_A (b) graf_B (c) graf_C (d) graf_D (e) graf_E (f) graf_F

(a) leuven_A (b) leuven_B (c) leuven_C (d) leuven_D (e) leuven_E (f) leuven_F

使用Shi-Tomasi-SURFORB算法对仿真实验的待匹配图像进行角点检测检测，角点特征检测结果图如图10—图13所示，其中图10表示对图2中boat图像的角点特征检测结果图，图11表示对图3中bikes图像的角点特征检测结果图，图12表示对图4中graf图像的角点特征检测结果图，图13表示对图5中leuven图像的角点特征检测结果图。

(a) boat A-B (b) boat B-C (c) boat C-D (d) boat D-E (e) boat E-F

(a) bikes A-B (b) bikes B-C (c) bikes C-D (d) bikes D-E (e) bikes E-F

(a) graf A-B (b) graf B-C (c) graf C-D (d) graf D-E (e) graf E-F

(a) leuven A-B (b) leuven B-C (c) leuven C-D (d) leuven D-E (e) leuven E-F

使用传统ORB算法对仿真实验的待匹配图像进行角点特征匹配，图像角点特征匹配结果图如图14—图17所示，其中图14表示对图2中boat图像的角点特征匹配结果图，图15表示对图3中bikes图像的角点特征匹配结果图，图16表示对图4中graf图像的角点特征匹配结果图，图17表示对图5中leuven图像的角点特征匹配结果图，其中boat A-B表示对图2中boat_A与boat_B进行图像角点特征匹配的结果图，其他情况以此类推。

(a) boat A-B (b) boat B-C (c) boat C-D (d) boat D-E (e) boat E-F

(a) bikes A-B (b) bikes B-C (c) bikes C-D (d) bikes D-E (e) bikes E-F

(a) graf A-B (b) graf B-C (c) graf C-D (d) graf D-E (e) graf E-F

(a) leuven A-B (b) leuven B-C (c) leuven C-D (d) leuven D-E (e) leuven E-F

使用Shi-Tomasi-SURFORB算法对仿真实验的待匹配图像进行角点特征匹配，图像角点特征匹配结果如图18—图21所示，其中图18表示对图2中boat图像的角点特征匹配结果图，图19表示对图3中bikes图像的角点特征匹配结果图，图20表示对图4中graf图像的角点特征匹配结果图，图21表示对图5中leuven图像的角点特征匹配结果图，其中boatA-B表示对图2中boat_A与boat_B进行图像角点特征匹配的结果图，其他情况以此类推。

仿真实验为了比较传统ORB算法与Shi- Tomasi-SURFORB算法之间的执行效率，对图像角点特征检测数目、图像角点特征匹配数目、图像角点特征正确匹配数目、图像角点特征匹配精度、图像角点特征匹配精度率、图像角点特征匹配时间和图像角点特征匹配时间率共7个参数进行统计，其中图像角点特征的匹配精度率、图像角点特征的匹配时间率计算如下：

(9)

其中，Pm表示图像角点特征的匹配精度率，MShi-Tomasi-SURFORB表示Shi-Tomasi-SURFORB算法的图像角点特征的匹配精度，MORB表示传统ORB算法的图像角点特征的匹配精度。

(10)

其中，Pt表示图像角点特征的匹配时间率，TShi-Tomasi-SURFORB表示Shi-Tomasi-SURFORB算法的图像角点特征的匹配时间，TORB表示传统ORB算法的图像角点特征的匹配时间。

仿真实验统计数据的对比分析如图22所示，根据图22(d)所知，与传统ORB算法相比，Shi-Tomasi-SURFORB算法的角点特征匹配精度有一定的提升，根据图22(e)所知，与传统ORB算法相比，Shi-Tomasi-SURFORB算法的角点特征匹配时间有一定的提升，根据图22(f)所知，与传统ORB算法相比，图像角点特征匹配时间率平均提升了9.46%，图像角点特征匹配精度率平均提升了8.88%，Shi-Tomasi-SURFORB算法在图像角点特征匹配精度和匹配时间两方面更加均衡。

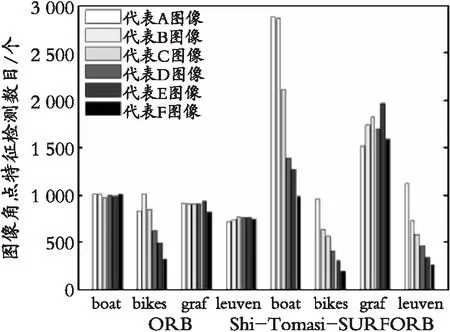
(a) 图像角点特征检测数目对比图

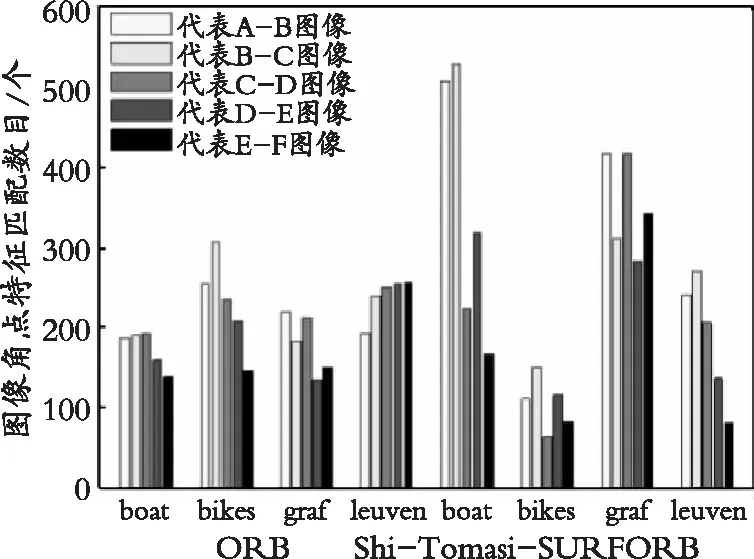
(b) 图像角点特征匹配数目对比图

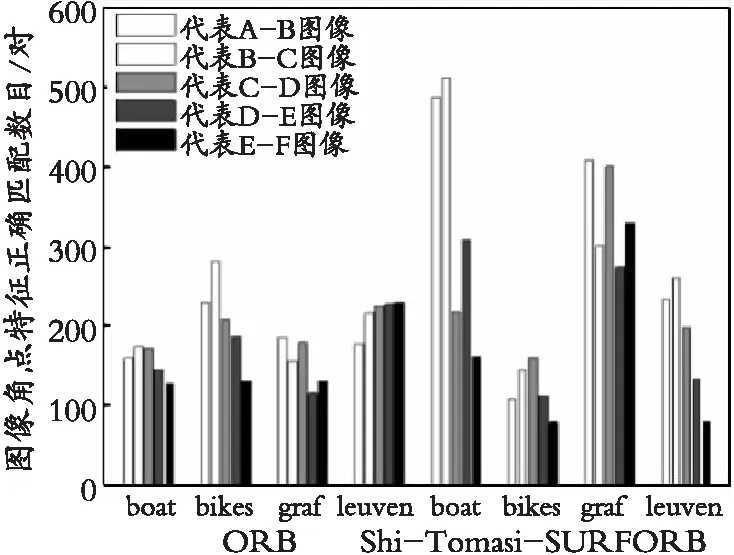
(c) 图像角点特征正确匹配数目对比图

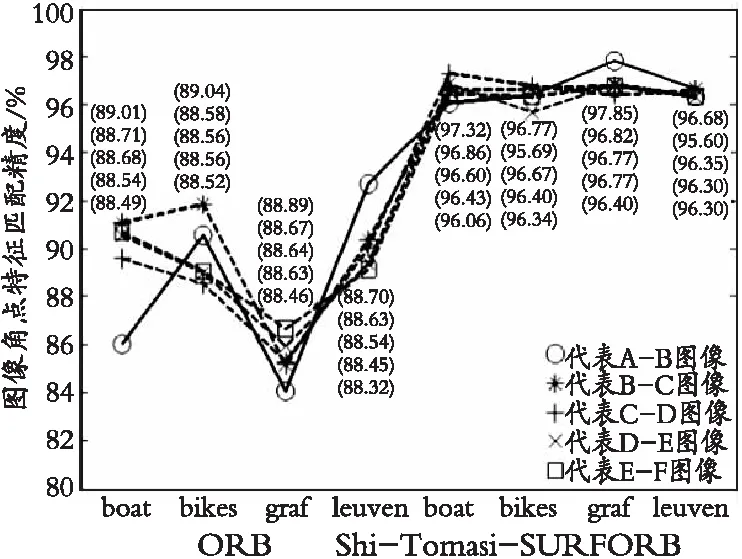
(d) 图像角点特征匹配精度对比图

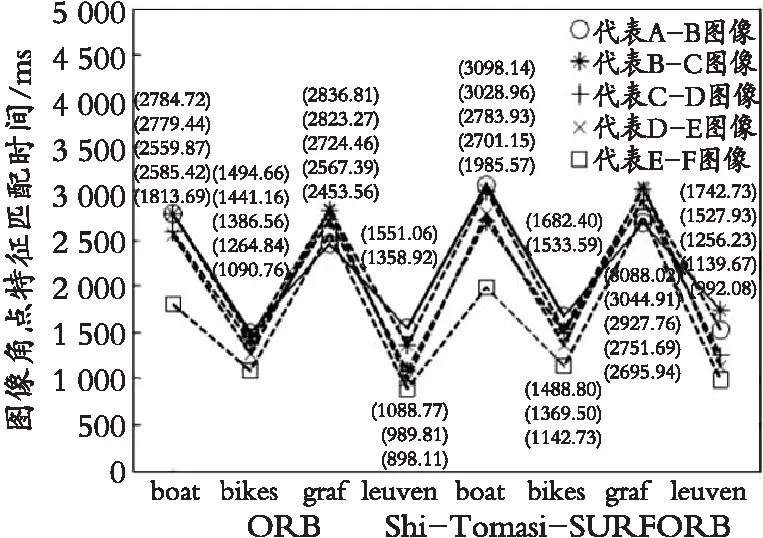
(e) 图像角点特征匹配时间对比图

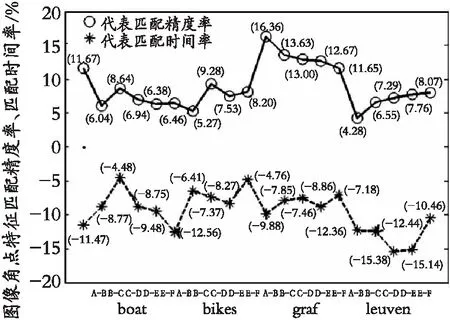
(f) 相比传统ORB算法的Shi-Tomasi-SURFORB算法的图像角点特征匹配精度率、匹配时间率对比图

其中，图22(a)表示图像角点特征检测数目对比图，图22(b)表示图像角点特征匹配数目对比图，图22(c)表示图像角点特征正确匹配数目对比图，图22(d)表示图像角点特征匹配精度对比图，图22(e)表示图像角点特征匹配时间对比图，图22(f)表示相比传统ORB算法的Shi-Tomasi-SURFORB算法的图像角点特征匹配精度率、匹配时间率对比图。

3 结束语

提出了Shi-Tomasi-SURFORB算法，针对传统ORB算法存在的角点特征匹配精度不高的问题，使用Shi-Tomasi算法、BRIEF和SURF相融合算法、随机投影原理与优化的匹配算法进行优化，得到的结论有3点：图像角点特征匹配时间有一定提升；图像角点特征匹配精度也有一定提升；图像角点特征匹配时间与图像角点特征匹配精度提升程度相当。综上所述，Shi-Tomasi-SURFORB算法为在图像角点特征匹配精度和耗时两方面均衡的场景提供了一种均衡的解决方案，下一步研究重点是在图像角点特征匹配时间相当甚至降低的情况下，提升图像角点特征匹配精度。