欠驱动无人船的运动控制设计*

李欧雪， 周宇生

(贵州大学 数学与统计学院，贵阳 550025)

0 引 言

无人船技术及其产品具有广阔的市场前景[1]，如在海面污染状况检测、清污作业、水面远程医疗服务和特殊海洋环境作业等领域具有不可替代的作用。无人船系统是一种典型的二阶非完整约束动力系统，其输入控制量为前向推力和旋转力矩。为了使三自由度欠驱动无人船在复杂的环境中具有灵活的航行能力，则需要解决欠驱动无人船的精确轨迹跟踪控制问题。然而，由于非完整约束和欠驱动因素的影响，导致其轨迹跟踪问题变得困难。关于欠驱动无人船的轨迹跟踪控制问题，国内外已经积累了大量的控制方法，如PID控制、反馈线性化控制、模糊控制、神经网络控制、自适应控制、滑模控制和Backstepping控制等。但这些方法在欠驱动和非完整约束下控制精度难以满足需求。例如：文献[2-3]为实现欠驱动船舶在模型参数不确定和外界风浪流干扰情况下水平面的航迹跟踪控制， 提出了滑模鲁棒控制方法，实现欠驱动船舶在模型参数不确定和外界风浪流干扰情况下水平面的航迹跟踪控制。文献[4]针对船舶航向非线性系统，提出了一种基于神经网络方法的鲁棒跟踪控制器，仿真结果表明其具有较好的控制性能。文献[5-6]主要设计Backstepping控制律，利用李雅普诺夫稳定性理论证明船舶位置信息的全局指数稳定，对船舶进行轨迹跟踪控制。文献[7-8]研究了船舶控制的PID控制算法，通过仿真计算结果说明了PID控制算法的有效性。文献[9]为了实现船舶航迹控制，提出了一种鲁棒自适应控制算法，并通过仿真验证了所提出的控制器的有效性。然而，这些文献中的控制方法有些仅仅考虑了运动学方程；有些虽然同时考虑了运动学方程和动力学方程，但需要建立精确的动力学模型才能获得较高的控制精度，而欠驱动无人船的动力学模型复杂，难以精确建模。因此，为了从根本上解决轨迹跟踪精确性问题，必须深入理解无人船运动规律，将其运动学方程和动力学方程有机结合起来设计控制器。

主要针对三自由度欠驱动无人船的轨迹跟踪控制问题进行研究。通过从理论上分析欠驱动无人船在非完整约束下的运动规律[10]，设计曲率跟踪目标。将其与欠驱动无人船的数学模型相结合设计基于逆动力学的自适应轨迹跟踪控制器。所提出的控制方法充分利用了欠驱动无人船在非完整约束下的运动规律，从根本上解决了轨迹跟踪的精确性问题。

1 欠驱动无人船运动学方程

欠驱动无人船的状态由其重心O在惯性坐标系的位置(x，y)及偏航角φ来表示。

p=(x，y，φ)T，q=(υ，ω)T

由于欠驱动无人船只有控制输入前向推力Tυ和旋转力矩Tω，所以欠驱动无人船的运动状态依靠前向速度υ和偏航转速ω。

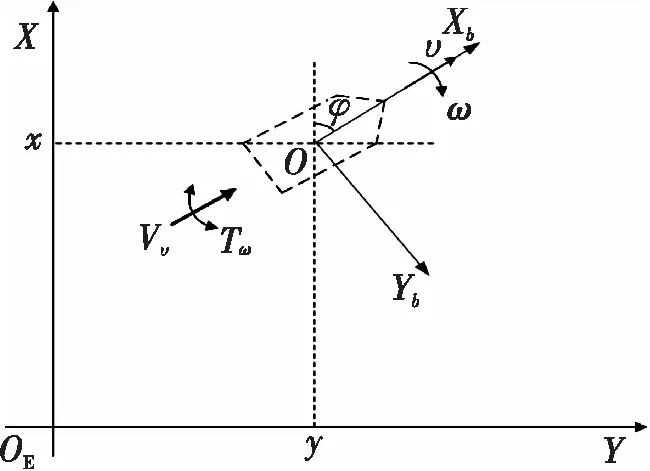
图1 欠驱动无人船结构简图Fig. 1 Schematic diagram of the underactuated unmanned ship

若重心O的轨迹曲线连续光滑，则Yb方向上的速度为0。反之，若在某时刻t0，Yb方向上的速度不为0，则该时刻会产生不可导点，导致轨迹曲线不光滑。因此欠驱动无人船做光滑轨迹运动时需要满足条件

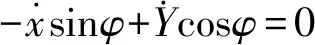
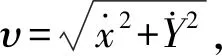
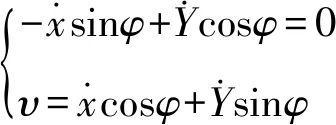
(1)

由式(1)可知，点O的轨迹切向量υ就是前向速度。将式(1)转化可以得到

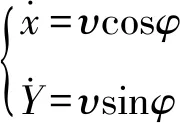
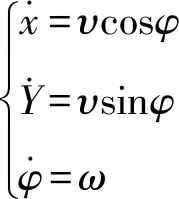
2 欠驱动无人船动力学方程

利用文[11]介绍的小型SUV三自由度MMG模型，文献[12-15]介绍的相关模型系数，得到欠驱动无人船的动力学方程为

对附加质量mbx和附加惯性矩Ibz的图谱多元回归分析，得到：

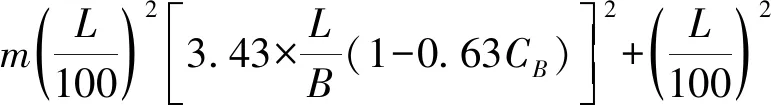
I=m×[0.35×B]2

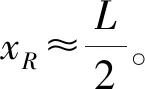
因此欠驱动无人船的动力学方程为

(2)

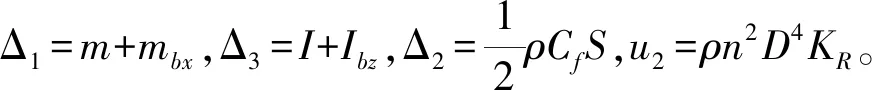
3 轨迹跟踪控制系统设计

3.1 动态跟踪目标设计

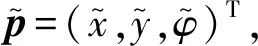
(3)

对式(3)关于t求导得

前两式交叉相乘并相减得到

则点O的速度和轨迹位姿的关系为

(4)

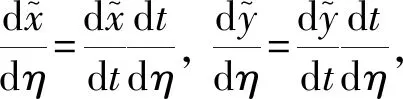
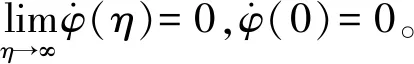
其中α>0，β>0，r>0。

(5)

由式(5)可知α=l2β，r=l。

φ(η)=-(βη+1)le-βη+l

其中l为轨迹长度，若以s为新变量可得到

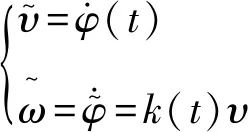
(6)

其中υ是实际前向速度。

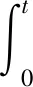
称式(6)为动态跟踪目标，由式(6)可知，其前向速度目标可减小开始时刻的速度误差，提高动态轨迹跟踪控制效果。

3.2 偏航转速控制系统

由动力学方程式(2)可知

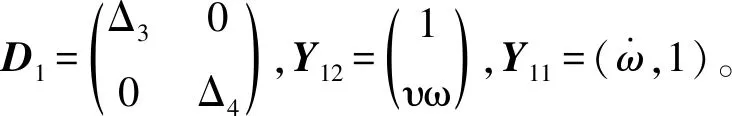
设计基于逆动力学的自适应控制律

(7)

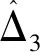
为调整系数k1使系统稳定，上式写为

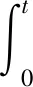
V=X1TD1X1+Y12TD1eTΓ1D1eY12

(8)

其中Γ1为正定对称矩阵,对V关于t求导

则有

(9)

为了提高偏航转速系统鲁棒性，设计控制系统基础部分u10和切换控制部分u11为

其中S1(ω(0))=0，G1是合适的常数，ε是外部扰动最大幅度，μ是滑模控制参数。

因此，可以得到u1=u10+u11。

3.3 前向速度控制系统

由动力学方程式(2)可知

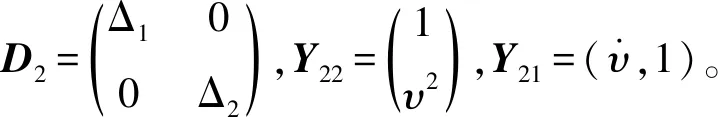
设计基于逆动力学的自适应控制律

(10)

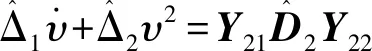
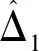
为调整系数k2使系统稳定，上式写为

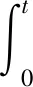
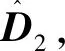
V=X2TD2X2+Y22TD2eTΓ2D2eY22

(11)

其中Γ2为正定对称矩阵,对V关于t求导

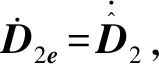
则有

(12)

类似地，控制系统基础部分u20和切换控制部分u21设计为

其中S2(υ(0))=0，G2是合适的常数，

则可以设计u2=u20+u21。

4 仿真实现

由式(4)设计静态速度目标

(13)

由式(6)设计动态跟踪目标为

(14)

假设参数[16]：KR=0.35，AR=1.14 m2，D=0.18 m，λ=1.3，L=2.6 m，CB=0.765，τ=0.25，S=3.3 m2，KF=0.6，B=1.2 m，d=0.1 m，ρ=1 000 kg/m3。

如图2，图3所示，采用静态跟踪目标式(13)时累积速度误差远远大于采用动态轨迹跟踪目标式(14)时的累积速度误差。而累积速度误差会影响累积位姿误差，使得实际轨迹位姿和目标轨迹位姿产生误差。

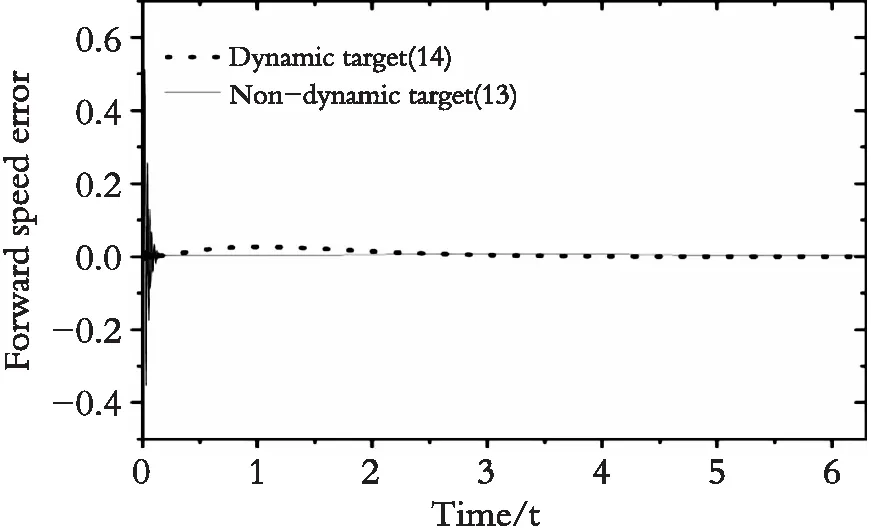
图2 欠驱动无人船的前向速度误差Fig. 2 Forward speed error of the underactuated unmanned ship

图3 欠驱动无人船的偏航转速误差Fig. 3 Yaw rotation speed error of the underactuated unmanned ship

如图4所示，采用静态目标式(13)时，累积位姿误差越来越大，其原因在于开始时刻的速度误差值很大，又不能调节其累积位姿误差。但是采用动态轨迹跟踪目标式(14)，其前行速度目标是根据实际需求来设计的，在开始时刻的速度误差为0，而且能调节累积速度速度误差，从而避免累积位姿误差较大，因此，采用动态轨迹跟踪目标可以使欠驱动无人船更加精确地沿着目标轨迹运动。

图4 欠驱动无人船在平面上的实际运动轨迹Fig. 4 Actual motion trajectory of the underactuated unmanned ship on the plane

5 小 结

先从运动学和动力学两方面推导了欠驱动无人船的数学模型，分析欠驱动无人船在非完整约束下的运动规律。然后，将欠驱动无人船的目标轨迹转化为由相对曲率设计与欠驱动无人船动力学方程匹配的动态轨迹跟踪目标，这样原问题就可以转化为一个简单的轨迹跟踪控制问题。该方法能够减少了误差系统在初始时刻的速度误差，并且能动态地调整了误差系统的累积速度误差，使整个运动过程中累积位姿误差尽量小。最后设计基于逆动力学的自适应轨迹跟踪控制器，将动态跟踪目标设计为积分滑模面，增加积分滑模切换控制部分，使得最终设计的力矩控制器具有很强的鲁棒性。从仿真结果可以看出采用本文方法能够极大地减少速度误差，并且使得实际运动轨迹与目标轨迹基本能够重合。

本文所提出的方法能够从根本上解决欠驱动无人船轨迹跟踪的精确性问题，并具有很强的鲁棒性，对解决其他欠驱动非完整机械结构的精确运动控制问题具有一定的启发和参考价值。